Stochastische Ordnung
Stochastische Ordnungen sind Ordnungsrelationen für Zufallsvariablen. Sie verallgemeinern das Konzept von größer und kleiner auf zufällige Größen und dienen zum Beispiel dem Vergleich von Risiken in der Versicherungswirtschaft. Die Theorie der stochastischen Ordnungen ist ein jüngeres mathematisches Teilgebiet und hat in den letzten Jahrzehnten eine starke Entwicklung erfahren und eine breite Anwendung in Finanzmathematik, ökonomischer Forschung und Operations Research gefunden. Spezielle stochastische Ordnungen wurden schon in der Nachkriegszeit erforscht, die erste umfassende Monographie des Themas von Dietrich Stoyan wurde 1977 veröffentlicht. Es werden zahlreiche stochastische Ordnungen mit jeweils unterschiedlichen Anwendungsbereichen betrachtet, die Theorie der Integralordnungen ermöglicht es dabei, unterschiedliche Ordnungen mit einheitlichen Methoden zu untersuchen.
Ordnung im Mittel[Bearbeiten | Quelltext bearbeiten]
Eine in der Praxis oft genutzte Ad-hoc-Ordnung entsteht aus dem Vergleich von Erwartungswerten. Man sagt die reelle Zufallsvariable ist im Mittel kleiner als die Zufallsvariable , wenn gilt. Diese Ordnung berücksichtigt keine weiteren Eigenschaften der Verteilungen wie Varianz oder Schiefe.
Gewöhnliche stochastische Ordnung[Bearbeiten | Quelltext bearbeiten]
Eine besondere Rolle spielt die gewöhnliche stochastische Ordnung (engl.: usual stochastic order). Ausgehend von der Notwendigkeit, Bewertungen und Entscheidungen auch unter Unsicherheit vornehmen zu können, überträgt sie den anschaulichen Ordnungsbegriff reeller Zahlen (formalisiert durch die Ordnungsaxiome reeller Zahlen) auf reellwertige Zufallsvariablen. Sie wurde vor anderen stochastischen Ordnungen untersucht und 1947 (Mann und Whitney) und 1956 (Lehmann) in mathematischen Arbeiten verwendet. Von Samuel Karlin wurde sie 1960 in das Operations Research eingeführt. In der ökonomischen Literatur ist sie als first order stochastic dominance bekannt.[1]

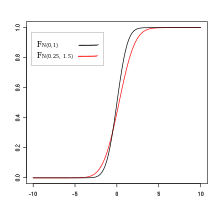
Definition: Seien und reelle Zufallsvariablen. ist größer-gleich bezüglich der gewöhnlichen stochastischen Ordnung, wenn für alle gilt
- .
Das heißt, für eine beliebige Schranke liegen die Werte von mit größerer (oder gleicher) Wahrscheinlichkeit über als die Werte von . Als Symbol wird häufig eingeführt. Das lässt sich ebenfalls als Kriterium für die Verteilungsfunktionen und formulieren:
- für alle .
Eine äquivalente Definition lautet
- für alle monoton wachsenden Funktionen .
Diese Definition lässt sich für Zufallsvariablen mit Werten in einem topologischen Raum , auf dem eine Halbordnung definiert ist, auf natürliche Weise verallgemeinern (wobei die Ordnung mit der Topologie verträglich sein muss und daher die Abgeschlossenheit der Menge gefordert wird.)
Seien zwei Zufallsvariablen mit Werten in einem halbgeordneten polnischen Raum. Der Satz von Strassen besagt nun, dass genau dann gilt, wenn zwischen den Variablen eine monotone Kopplung besteht. Das bedeutet, dass zwei (andere) Zufallsvariablen und existieren, welche dieselbe Verteilung wie resp. besitzen und für die außerdem gilt. Der Beweis dieser Existenzaussage ist außer in einfachen Fällen nicht konstruktiv.
Zufallsgrößen mit dem gleichen Erwartungswert und unterschiedlicher Verteilung kann man mit der gewöhnlichen stochastischen Ordnung nicht vergleichen, je nach Anwendung ist es erforderlich, andere stochastische Ordnungen zu betrachten.
Integralordnungen[Bearbeiten | Quelltext bearbeiten]
Viele stochastische Ordnungen von Interesse (für Zufallsvariablen mit Werten in einem geordneten polnischen Raum ) lassen sich ebenso wie die gewöhnliche stochastische Ordnung über Klassen von „Testfunktionen“ (mit )
- für alle für die beide Erwartungswerte definiert sind
definieren. Solche stochastischen Ordnungen heißen Integralordnungen, heißt die von generierte stochastische Ordnung, ihr Generator. Die so definierte Operation ist nicht unbedingt transitiv, eine Möglichkeit, dieses Problem zu umgehen, ist die Einschränkung auf solche Funktionen und Zufallsvariablen, für die alle Erwartungswerte existieren.
Dies ist eine wahrscheinlichkeitstheoretische Begriffsbildung – das heißt, es kommt nur auf die Verteilungen von und an und Integralordnungen lassen sich ebenso für Verteilungen auf geordneten polnischen Räumen ausgestattet mit der -Algebra der Borelmengen definieren:
- für alle für die beide Integrale definiert sind,
wobei Wahrscheinlichkeitsmaße auf seien.
Oft wird eine Ordnung schon von einer Unterklasse von generiert (es reicht also aus, die rechte Seite von für einen Teil der Funktionen aus überprüfen, um zu folgern), im Fall der gewöhnlichen stochastischen Ordnung zum Beispiel für alle isotonen messbaren Indikatorfunktionen oder für alle unendlich oft differenzierbaren isotonen Funktionen.
In der Anwendung der Ordnung ist oft von Interesse, aus der linken Seite von die Gültigkeit der rechten Seite für eine bestimmte Funktion zu folgern. Die Frage danach, für welche Funktionen dies möglich ist, führte A. W. Marshall 1991 zum Begriff des maximalen Generator.[2]
Bei der Bestimmung eines maximalen Generators wird wie bei der Sicherung der Transitivität eine Einschränkung auf bestimmte Funktionen benötigt. Es werden eine Gewichtsfunktion eingeführt und nur -beschränkte Funktionen und Maße, bezüglich denen integrierbar ist, betrachtet.
Stop-loss order[Bearbeiten | Quelltext bearbeiten]
Die für die Versicherungsmathematik wichtige stop-loss order ist ein weiteres Beispiel für eine Integralordnung. Sie wird generiert von der Klasse der reellen Funktionen der Gestalt , . Die stop-loss order ist schwächer als die gewöhnliche stochastische Ordnung und wird unter anderem beim Vergleich von Schadenssummen und als Kriterium bei der Wahl eines Prämienprinzips eingesetzt. Werden und als Risiken interpretiert, bedeutet , dass die Stop-Loss-Rückversicherungsprämie für das Risiko größer ist als die für bei jeder Wahl des Selbstbehalts .[3]
Abhängigkeitsordnungen[Bearbeiten | Quelltext bearbeiten]
Auf einem Maßraum betrachte man zwei Zufallsvektoren und von , so ist über den Vergleich der Kovarianzen
ein Vergleich des Grades der gegenseitigen Abhängigkeit der Komponenten der beiden Vektoren möglich. Abhängigkeitsordnungen (engl. dependence orders) verallgemeinern dieses Konzept und sind unter anderem von Interesse für die Versicherungswirtschaft, wo Häufung und Abhängigkeit von Risiken wie Hagel- oder Hochwasserschäden ein finanzielles Risiko für die Versicherer darstellen und die traditionell in der Versicherungsmathematik gemachte Annahme der Unabhängigkeit der Risiken zu einer Unterschätzung der Ruin-Wahrscheinlichkeit führt.
Zu den Abhängigkeitsordnungen gehört die supermodulare Ordnung . Sie wird generiert von der Klasse der supermodularen Funktionen
- . Mit dieser Definition, ist jede zweimal stetig differenzierbare reellwertige Funktion die auf den reellen Zahlen definiert ist, bereits supermodular. Dies wiederum hat zur Folge, dass nur -wertige Zufallsvektoren bezüglich verglichen werden können, die gleiche Randverteilungen besitzen.
Sie ermöglicht zusammen mit der stop-loss order den Vergleich von multivariaten Risiko-Portfolios mit abhängigen Risiken.
Genauer gilt: Seien und zwei Risiko-Portfolios mit gleichen Randverteilungen. Ist der Vektor der Risiken von Portfolio supermodular kleiner als der von Portfolio , ist die Zufallsvariable der Schadenssumme von Portfolio kleiner als die von Portfolio bezüglich der stop-loss order, und damit auch der Preis einer Stop-Loss-Rückversicherung:[4]
- .
Literatur[Bearbeiten | Quelltext bearbeiten]
- Alfred Müller, Dietrich Stoyan: Comparison methods for stochastic models and risks. Wiley, Chichester 2002, ISBN 0-471-49446-1.
- Klaus D. Schmidt: Versicherungsmathematik. 2., durchgesehene Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-29097-4.
- Dietrich Stoyan: Qualitative Eigenschaften und Abschätzungen stochastischer Modelle. Lizenzausgabe. R. Oldenbourg, München u. a. 1977, ISBN 3-486-21271-0.
- R. Szekli: Stochastic Ordering and Dependence in Applied Probability (= Lecture Notes in Statistics. Vol. 97). Springer, New York u. a. 1995, ISBN 0-387-94450-8.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Alfred Müller, Dietrich Stoyan: Comparison methods for stochastic models and risks. Wiley, Chichester 2002, ISBN 0-471-49446-1, S. 2.
- ↑ Albert W. Marshall: Multivariate Stochastic Orderings and Generating Cones of Functions. In: K. Mosler, M. Scarsini (Hrsg.): Stochastic Orders and Decision under Risk (= IMS Lecture Notes – Monograph Series. Bd. 19). Institute of Mathematical Statistics, Hayward CA 1991, ISBN 0-940600-26-9, S. 231–247.
- ↑ Nicole Bäuerle, Alfred Müller: Modeling and Comparing Dependencies in Multivariate Risk Portfolios. In: ASTIN Bulletin International Actuarial Association. Vol. 28, Nr. 1, 1998, ISSN 0515-0361, S. 59–76, hier S. 62, (pdf; 812 KB).
- ↑ Nicole Bäuerle, Alfred Müller: Modeling and Comparing Dependencies in Multivariate Risk Portfolios. In: ASTIN Bulletin International Actuarial Association. Vol. 28, Nr. 1, 1998, ISSN 0515-0361, S. 59–76, hier S. 64, (pdf; 812 KB).


![{\displaystyle \mathbb {E} [X]<\mathbb {E} [Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1be7609976f029571ffc8236d2ab7153588719)







![{\displaystyle X\preceq _{st}Y:\Leftrightarrow \mathbb {E} [f(X)]\leq \mathbb {E} [f(Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fac6b4373374b56ed5c189e788a4480b1a9f2e2)










![{\displaystyle (\star )\quad X\preceq _{\mathcal {F}}Y:\Leftrightarrow \mathbb {E} [f(X)]\leq \mathbb {E} [f(Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc66b3722f1489f912615689f832f24ae3e8213)



























