„Ebenengleichung“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
AZ: Weiterleitung nach Ebene (Mathematik)#Ebenengleichung erstellt |
Quartl (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Eine '''Ebenengleichung''' ist in der [[Mathematik]] eine [[Gleichung]], die eine [[Ebene (Mathematik)|Ebene]] beschreibt. Eine Ebene besteht dabei aus denjenigen [[Punkt (Geometrie)|Punkten]] in einem [[Kartesisches Koordinatensystem|kartesischen Koordinatensystem]], deren [[Koordinaten]] die Ebenengleichung erfüllen. Man unterscheidet explizite Formen von Ebenengleichungen, bei denen jeder Punkt der Ebene direkt identifiziert wird, und implizite Formen, bei denen die Punkte der Ebene indirekt durch eine Bedingung charakterisiert werden. Zu den expliziten Formen gehören die [[Parameterform]] und die [[Dreipunkteform]], zu den impliziten Formen die [[Normalenform]], die [[Hessesche Normalform]], die [[Koordinatenform]] und die [[Achsenabschnittsform]]. |
|||
#REDIRECT [[Ebene (Mathematik)#Ebenengleichung]] |
|||
== Explizite Formen == |
|||
=== Parameterform === |
|||
{{Hauptartikel|Parameterdarstellung}} |
|||
[[Datei:Plane equation qtl1.svg|miniatur|Parameterform]] |
|||
Bei der Parameterform oder Punktrichtungsform wird eine Ebene durch einen [[Stützvektor]] <math>\vec r</math> und zwei [[Richtungsvektor]]en <math>\vec u</math> und <math>\vec v</math> beschrieben: |
|||
:<math>E = \{ \vec x \in \R^3 \mid \vec x = \vec r + \mu \cdot \vec u + \lambda \cdot \vec v ~\text{für}~ \mu,\lambda \in \R \}</math>. |
|||
Der Stützvektor ist dabei der [[Ortsvektor]] eines beliebigen Punkts in der Ebene, auch Aufpunkt genannt. Die beiden Richtungsvektoren müssen in der Ebene liegen und dürfen nicht [[Kollinearität|kollinear]] sein, das heißt <math>\vec u</math> darf sich nicht als [[Vielfaches]] von <math>\vec v</math> schreiben lassen und umgekehrt. |
|||
=== Dreipunkteform === |
|||
[[Datei:Plane equation qtl2.svg|miniatur|Dreipunkteform]] |
|||
Bei der Dreipunkteform wird eine Ebene durch die Ortsvektoren <math>\vec r</math>, <math>\vec s</math> und <math>\vec t</math> dreier Punkte der Ebene beschrieben: |
|||
:<math>E = \{ \vec x \in \R^3 \mid \vec x = \vec r + \mu \cdot (\vec s - \vec r) + \lambda \cdot (\vec t - \vec r) ~\text{für}~ \mu,\lambda \in \R \}</math>. |
|||
Die drei Punkte dürfen dabei nicht alle auf einer [[Gerade]]n liegen. Aus der Dreipunkteform erhält man die Punktrichtungsform, indem man einen der drei Punkte als Aufpunkt auswählt und als Richtungsvektoren die [[Vektor|Verbindungsvektoren]] von diesem Punkt zu den anderen beiden Punkten wählt. |
|||
== Implizite Formen == |
|||
=== Normalenform === |
|||
{{Hauptartikel|Normalengleichung}} |
|||
[[Datei:Plane equation qtl3.svg|miniatur|Normalenform]] |
|||
Bei der Normalenform wird eine Ebene durch einen Stützvektor <math>\vec r</math> und einen [[Normalenvektor]] <math>\vec n</math> beschrieben: |
|||
:<math>E = \{ \vec x \in \R^3 \mid ( \vec x - \vec r ) \cdot \vec n = 0 \}</math>. |
|||
Hierbei bezeichnet <math>\cdot</math> das [[Skalarprodukt]] zweier Vektoren. Aus zwei nicht kollinearen Richtungsvektoren der Ebene <math>\vec u</math> und <math>\vec v</math> lässt sich ein Normalenvektor über das [[Kreuzprodukt]] <math>\vec n = \vec u \times \vec v</math> ermitteln. In der Normalenform besteht eine Ebene demnach aus denjenigen Punkten, für die der Differenzvektor aus Ortsvektor und Stützvektor [[Orthogonalität|senkrecht]] zum Normalenvektor der Ebene steht. |
|||
=== Hessesche Normalform === |
|||
{{Hauptartikel|Hessesche Normalform}} |
|||
[[Datei:Plane equation qtl4.svg|miniatur|Hessesche Normalform]] |
|||
Bei der hesseschen Normalform wird eine Ebene durch einen [[Einheitsvektor|normierten]] und orientierten Normalenvektor <math>\vec n</math> und den Abstand vom [[Koordinatenursprung]] <math>d</math> beschrieben: |
|||
:<math>E = \{ \vec x \in \R^3 \mid \vec x \cdot \vec n = d \}</math>. |
|||
Der Normalenvektor muss hierbei die [[Vektor#Länge/Betrag eines Vektors|Länge]] eins haben und vom Koordinatenursprung in Richtung der Ebene zeigen. Man erhält die hessesche Normalform aus der Normalenform durch Orientierung und Normierung des Normalenvektors sowie durch anschließende Wahl von <math>d = \vec r \cdot \vec n</math>. Die hessesche Normalform erlaubt eine effiziente Berechnung der [[Abstand|Abstände]] beliebiger Punkte im Raum zu der Ebene. |
|||
=== Koordinatenform === |
|||
{{Hauptartikel|Koordinatenform}} |
|||
[[Datei:Plane equation qtl6.svg|miniatur|Koordinatenform]] |
|||
Bei der Koordinatenform wird eine Ebene durch vier reelle Zahlen <math>a</math>, <math>b</math>, <math>c</math> und <math>d</math> in Form einer [[Lineare Gleichung|linearen Gleichung]] beschrieben: |
|||
:<math>E = \{ \vec x \in \R^3 \mid a \cdot x_1 + b \cdot x_2 + c \cdot x_3 = d \}</math>. |
|||
Hierbei muss mindestens eine der drei Zahlen <math>a,b,c</math> ungleich null sein. Die Koordinatenform entspricht der Normalenform, wobei <math>a</math>, <math>b</math> und <math>c</math> die Komponenten des (nicht notwendigerweise normierten) Normalenvektors <math>\vec n = (a,b,c)</math> sind und wiederum <math>d = \vec r \cdot \vec n</math> gesetzt wird. |
|||
=== Achsenabschnittsform === |
|||
{{Hauptartikel|Achsenabschnittsform}} |
|||
[[Datei:Plane equation qtl5.svg|miniatur|Achsenabschnittsform ]] |
|||
Bei der Achsenabschnittsform wird eine Ebene durch drei Achsenabschnitte <math>a_1</math>, <math>a_2</math> und <math>a_3</math> beschrieben: |
|||
:<math>E = \left\{ \vec x \in \R^3 ~ \big| ~ \frac{x_1}{a_1} + \frac{x_2}{a_2} + \frac{x_3}{a_3} = 1 \right\}</math>. |
|||
Hierbei sind <math>(a_1,0,0)</math>, <math>(0,a_2,0)</math> und <math>(0,0,a_3)</math> die Schnittpunkte der Ebene mit den drei [[Koordinatenachse]]n. Die Achsenabschnittsform kann aus der Koordinatenform mittels Division durch <math>d</math> errechnet werden. Verläuft eine Ebene parallel zu einer der Koordinatenachsen, fällt der entsprechende Term in der Achsenabschnittsform weg. |
|||
== Siehe auch == |
|||
* [[Geradengleichung]] |
|||
* [[Koordinatenebene]] |
|||
* [[Ursprungsebene]] |
|||
== Literatur == |
|||
* {{Literatur|Autor=Steffen Goebbels, Stefan Ritter|Titel=Mathematik verstehen und anwenden|Verlag=Springer|Jahr=2011|ISBN=978-3-827-42762-5}} |
|||
* {{Literatur|Autor=Lothar Papula|Titel=Mathematische Formelsammlung: Für Ingenieure und Naturwissenschaftler|Verlag=Springer|Jahr=2009|ISBN=978-3-834-89598-1}} |
|||
* {{Literatur|Autor=Thomas Westermann|Titel=Mathematik für Ingenieure|Verlag=Springer|Jahr=2008|ISBN=978-3-54077-731-1}} |
|||
== Weblinks == |
|||
* {{MathWorld|title=Plane|id=Plane}} |
|||
* {{PlanetMath|author=pahio|title=equation of plane|id=equationofplane}} |
|||
[[Kategorie:Analytische Geometrie]] |
[[Kategorie:Analytische Geometrie]] |
||
Version vom 9. Februar 2014, 23:00 Uhr
Eine Ebenengleichung ist in der Mathematik eine Gleichung, die eine Ebene beschreibt. Eine Ebene besteht dabei aus denjenigen Punkten in einem kartesischen Koordinatensystem, deren Koordinaten die Ebenengleichung erfüllen. Man unterscheidet explizite Formen von Ebenengleichungen, bei denen jeder Punkt der Ebene direkt identifiziert wird, und implizite Formen, bei denen die Punkte der Ebene indirekt durch eine Bedingung charakterisiert werden. Zu den expliziten Formen gehören die Parameterform und die Dreipunkteform, zu den impliziten Formen die Normalenform, die Hessesche Normalform, die Koordinatenform und die Achsenabschnittsform.
Explizite Formen
Parameterform

Bei der Parameterform oder Punktrichtungsform wird eine Ebene durch einen Stützvektor und zwei Richtungsvektoren und beschrieben:
- .
Der Stützvektor ist dabei der Ortsvektor eines beliebigen Punkts in der Ebene, auch Aufpunkt genannt. Die beiden Richtungsvektoren müssen in der Ebene liegen und dürfen nicht kollinear sein, das heißt darf sich nicht als Vielfaches von schreiben lassen und umgekehrt.
Dreipunkteform
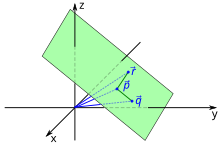
Bei der Dreipunkteform wird eine Ebene durch die Ortsvektoren , und dreier Punkte der Ebene beschrieben:
- .
Die drei Punkte dürfen dabei nicht alle auf einer Geraden liegen. Aus der Dreipunkteform erhält man die Punktrichtungsform, indem man einen der drei Punkte als Aufpunkt auswählt und als Richtungsvektoren die Verbindungsvektoren von diesem Punkt zu den anderen beiden Punkten wählt.
Implizite Formen
Normalenform

Bei der Normalenform wird eine Ebene durch einen Stützvektor und einen Normalenvektor beschrieben:
- .
Hierbei bezeichnet das Skalarprodukt zweier Vektoren. Aus zwei nicht kollinearen Richtungsvektoren der Ebene und lässt sich ein Normalenvektor über das Kreuzprodukt ermitteln. In der Normalenform besteht eine Ebene demnach aus denjenigen Punkten, für die der Differenzvektor aus Ortsvektor und Stützvektor senkrecht zum Normalenvektor der Ebene steht.
Hessesche Normalform

Bei der hesseschen Normalform wird eine Ebene durch einen normierten und orientierten Normalenvektor und den Abstand vom Koordinatenursprung beschrieben:
- .
Der Normalenvektor muss hierbei die Länge eins haben und vom Koordinatenursprung in Richtung der Ebene zeigen. Man erhält die hessesche Normalform aus der Normalenform durch Orientierung und Normierung des Normalenvektors sowie durch anschließende Wahl von . Die hessesche Normalform erlaubt eine effiziente Berechnung der Abstände beliebiger Punkte im Raum zu der Ebene.
Koordinatenform

Bei der Koordinatenform wird eine Ebene durch vier reelle Zahlen , , und in Form einer linearen Gleichung beschrieben:
- .
Hierbei muss mindestens eine der drei Zahlen ungleich null sein. Die Koordinatenform entspricht der Normalenform, wobei , und die Komponenten des (nicht notwendigerweise normierten) Normalenvektors sind und wiederum gesetzt wird.
Achsenabschnittsform
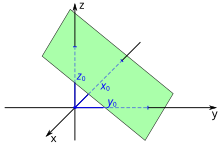
Bei der Achsenabschnittsform wird eine Ebene durch drei Achsenabschnitte , und beschrieben:
- .
Hierbei sind , und die Schnittpunkte der Ebene mit den drei Koordinatenachsen. Die Achsenabschnittsform kann aus der Koordinatenform mittels Division durch errechnet werden. Verläuft eine Ebene parallel zu einer der Koordinatenachsen, fällt der entsprechende Term in der Achsenabschnittsform weg.
Siehe auch
Literatur
- Steffen Goebbels, Stefan Ritter: Mathematik verstehen und anwenden. Springer, 2011, ISBN 978-3-8274-2762-5.
- Lothar Papula: Mathematische Formelsammlung: Für Ingenieure und Naturwissenschaftler. Springer, 2009, ISBN 978-3-8348-9598-1.
- Thomas Westermann: Mathematik für Ingenieure. Springer, 2008, ISBN 978-3-540-77731-1.
Weblinks
- Eric W. Weisstein: Plane. In: MathWorld (englisch).
- pahio: equation of plane. In: PlanetMath. (englisch)


























