Anharmonischer Oszillator
Der anharmonische Oszillator ist ein schwingungsfähiges physikalisches System, bei dem die Rückstellkraft nicht proportional zur Auslenkung aus der Ruhelage ist. Das hat zur Folge, dass die freie Schwingung nicht streng sinusförmig verläuft. Mechanische Beispiele sind etwa Pendel (Anharmonizität bemerkbar bei größerer Auslenkung), transversal schwingende Saiten, Kippschwingungen (das Kippeln eines aufrecht stehenden Gegenstands), Hüpfen eines Balls auf einer ebenen Fläche.
Bei genauer Betrachtung sind praktisch alle realen schwingungsfähigen Systeme anharmonisch. Die meisten nähern sich aber einem harmonischen Oszillator an, je kleiner die Auslenkungen aus der Ruhelage sind, weil dann die Näherung einer linearen Rückstellkraft immer besser zutrifft (für die Mechanik siehe Hookesches Gesetz, Mathematisches Pendel). Bei solchen anharmonischen Oszillatoren verlaufen kleine freie Schwingungen näherungsweise sinusförmig und mit einer bestimmten Eigenfrequenz, der Grundfrequenz des Oszillators.
Beim anharmonischen Oszillator treten im Vergleich zum harmonischen Oszillator grundsätzlich neue Phänomene auf:
- Die Abweichung von der Sinusform bedeutet, dass die Schwingung auch Oberschwingungen (akustisch: Obertöne) der Grundfrequenz enthält. Bei harmonischer Anregung mit der Grundfrequenz klingen sie auch nach dem Einschwingvorgang nicht ab, sondern schwingen zusammen mit der Grundschwingung weiter.
- Bei unsymmetrischem Kraftgesetz verschiebt sich der Mittelpunkt der Schwingung gegenüber der Ruhelage. Dies tritt z. B. bei den Schwingungen zwischen den Atomen der festen Körper auf und ist die Ursache von deren thermischer Ausdehnung.
- Bei periodischer Anregung sind in der entstehenden erzwungenen Schwingung nicht nur, wie beim harmonischen Oszillator, die Anregungs- und die Eigenfrequenz enthalten, sondern zusätzlich deren Differenzfrequenz und Summenfrequenz sowie alle anderen ganzzahligen Kombinationen davon. Technische Anwendung findet dies z. B. in der nichtlinearen Optik bei der Frequenzverdopplung bei Laserlicht.
- Bei äußerer Anregung mit einer periodischen Kraft kann der anharmonische Oszillator auch mit einer chaotischen Bewegung reagieren, wenn die Anfangsbedingungen entsprechend gewählt sind oder seine Parameter außerhalb bestimmter Grenzen liegen (z. B. bei zu geringer Dämpfung). Siehe dazu: Doppelpendel
Bewegungsgleichung[Bearbeiten | Quelltext bearbeiten]
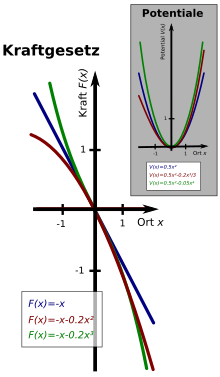

Es gibt eine Vielzahl unterschiedlicher anharmonischer Oszillatoren und entsprechend viele Bewegungsgleichungen. Außerdem gibt es Unterschiede, je nachdem ob das Problem aus der Mechanik, Akustik oder Elektrik stammt. Ihnen gemeinsam ist, dass ihre Rückstellkraft nicht wie beim harmonischen Oszillator gemäß nur linear von der Auslenkung abhängt, sondern auch von höheren Potenzen von („nichtlineares Kraftgesetz“). In der nebenstehenden Abbildung sind die einfachsten Beispiele zusammen mit dem genäherten linearen Kraftgesetz (blaue Gerade) dargestellt:
- A) Ein einfaches asymmetrisches Kraftgesetz (rote Kurve im Bild rechts) lautet .
- Eine Umformung lässt erkennen, dass der nichtlineare Term die Rückstellkraft zur einen Seite hin zunehmend schwächt und zur anderen Seite hin stärkt, sofern die Auslenkungen nicht zu groß werden (). Wie man an den Trajektorien in der zweiten Abbildung sieht, führt dies zu einer im Vergleich zum harmonischen Oszillator stärkeren Auslenkung des Oszillators in die Richtung der abgeschwächten Rückstellkraft und zu einer verlangsamten Periode. Ein solches asymmetrisches Kraftgesetz kann etwa als zweite Näherung (nach dem linearen Kraftgesetz) an das unten erwähnte Morse-Potential in der Molekülphysik genutzt werden.
- B) Ein einfaches symmetrisches Kraftgesetz (grüne Kurve im Bild rechts) lautet .
- Je nach Vorzeichen von wächst die Rückstellkraft, im Vergleich zum harmonischen Oszillator, zunehmend stärker () oder schwächer () an. Im ersten Fall erfolgen die Schwingungen bei gleicher Amplitude schneller, im zweiten Fall langsamer.
- Zum Beispiel ist dies Kraftgesetz für eine Näherung für das Schwere- oder mathematische Pendel, dessen Schwingungsperiode mit zunehmender Amplitude zunimmt. Die Größe steht in diesem Fall für den dimensionslosen Auslenkungswinkel des Pendels. Eine solche Näherung ergibt sich, wenn man die Rückstellkraft des mathematischen Pendels in einer Taylorreihe bis zur dritten Ordnung in entwickelt:
Die Bewegungsgleichungen mit dem Dämpfungsterm ergeben sich dann aus dem Newton’schen Gesetz
wobei die erste und die zweite Ableitung der Funktion nach der Zeit bezeichnet, zu:
- Fall A:
- Fall B:
Für erhält man wieder in beiden Fällen das lineare Kraftgesetz sowie die Differentialgleichung des gedämpften harmonischen Oszillators. Auch für kleine Auslenkungen ist die Lösung des anharmonischen Oszillators wieder nahezu harmonisch, wie die ersten Trajektorien in der Abbildung rechts zeigen.
Durch die Nichtlinearität der Differentialgleichungen wird das Superpositionsprinzip außer Kraft gesetzt. Das bedeutet, dass nicht mehr jedes Vielfache einer Lösung auch eine Lösung der Differentialgleichung ist und allgemeiner, dass mit zwei Lösungen nicht jede Linearkombination auch eine Lösung ist (wobei beliebige feste Zahlen sind). Die Lösung der Bewegungsgleichung ist meist ein elliptisches Integral und daher in geschlossener Form mit elementaren Funktionen nicht darstellbar. Dieser Artikel konzentriert sich auf periodische Bewegungen des anharmonischen Oszillators. Dabei wird die Dämpfung stellenweise vernachlässigt, d. h. gesetzt. Nur so ergeben sich, falls keine äußere Kraft einwirkt, periodische Bewegungen im strengen Sinne. Zu den chaotischen Bewegungsformen siehe Chaosforschung und dort angegebene Fachliteratur.
Näherungslösung[Bearbeiten | Quelltext bearbeiten]
Im Fall einer schwachen anharmonischen Störung, d. h. bzw. , kann man die Lösung durch Störungsrechnung erhalten. Dazu gibt man in Form einer Potenzreihe eines Störparameters an:
Dabei ist das erste Glied die (den Anfangsbedingungen angepasste) Lösung für den harmonischen Fall , z. B. , wenn der Oszillator zur Zeit bei der Auslenkung mit Geschwindigkeit freigegeben wird und die Grundfrequenz hat.
Nach Einsetzen von in die Bewegungsgleichung, wobei durch ausgedrückt wird, ergibt sich eine Potenzreihe in , deren Koeffizienten sämtlich gleich Null zu setzen sind. So erhält man Differentialgleichungen für die einzelnen Näherungsfunktionen , die rekursiv zu lösen sind. Konkret hat die Differentialgleichung für die Form der Bewegungsgleichung für einen harmonischen Oszillator, der von einer externen Kraft, welche durch die vorherigen gegeben ist, zu erzwungenen Schwingungen angeregt wird.
Im Fall A folgt im ersten Schritt
Hier tritt bereits die verdoppelte Grundfrequenz auf. Der mathematische Grund dafür lässt sich zurückverfolgen zum Auftreten des quadratischen Terms in der Bewegungsgleichung, der durch die trigonometrische Identität linearisiert wird. Bei den weiteren Näherungen ergeben sich Summanden mit entsprechend höheren Vielfachen der Grundfrequenz, insgesamt also ein ganzes Spektrum von Oberschwingungen.
Im Fall B ergibt sich im ersten Schritt eine instabile Lösung, denn enthält einen zu proportionalen Term. Dieser lässt sich jedoch eliminieren, wenn gesetzt wird. So ergibt sich schon in 1. Näherung eine Abhängigkeit der Oszillationsfrequenz von der Amplitude (wie im Fall A erst im 2. Schritt).
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Real in technischen Geräten verbaute Federn weisen im Allgemeinen, zuweilen auch durch die Konstruktion beabsichtigt, nur in gewissen Grenzen eine lineare Beziehung zwischen Rückstellkraft und Auslenkung auf. Die Dynamik eines Systems mit solchen Federn folgt dann den nichtlinearen Bewegungsgleichungen, wie sie oben eingeführt wurden.

Wichtige Anwendungen für anharmonische Schwingungen finden sich etwa in der Molekülphysik bei der Schwingung zweiatomiger Moleküle, oder in der Festkörperphysik bei wärmebedingten Schwingungen von Atomen. Die Anharmonizität bildet sich durch die unterschiedlichen Effekte bei Annäherung (elektrostatische Abstoßung, teilweise durch die Elektronen der Atomhülle abgeschirmt, aber durch das Pauli-Prinzip verstärkt) und Entfernung (Rückstellkraft durch die kovalente Bindung der Atome) der Atomrümpfe aus. Wie in der Abbildung rechts gezeigt, können solche Schwingungen etwa in einem Morse-Potential berechnet werden.
Erzwungene anharmonische Schwingungen[Bearbeiten | Quelltext bearbeiten]
Bei der Bewegung unter dem Einfluss einer zeitabhängigen äußeren Kraft unterscheiden sich anharmonischer und harmonischer Oszillator grundsätzlich voneinander. Beispielsweise kann, auch nach Beendigung eines Einschwingvorgangs, der anharmonische Oszillator mit anderen Frequenzen schwingen als in der erregenden Kraft vertreten. Es kann auch bei langsamer Variation der Erregerfrequenz zu sprunghafter Änderung der Amplitude kommen. Bei gekoppelten anharmonischen Oszillatoren kann eine minimale, kaum messbare Veränderung der Frequenz oder Amplitude zu starken Veränderungen des Verhaltens aller gekoppelten Elemente führen. Außerdem treten in solchen gekoppelten Systemen weitere Effekte wie das Frequenzziehen und die Frequenzmitnahme auf. Diese Phänomene sind auch praktisch von großem Interesse, da reale Oszillatoren sich nur solange annähernd harmonisch verhalten, wie bestimmte Grenzen für Auslenkung und/oder Frequenz eingehalten werden.
Diese Phänomene lassen sich ganz allgemein auf die nicht-lineare Form der Bewegungsgleichung zurückführen, womit das Superpositionsprinzip hier nicht mehr angewendet werden kann. Einige der Konsequenzen:
- Es gibt kein allgemein gültiges Lösungsverfahren wie bei den erzwungenen Schwingungen des harmonischen Oszillators. Man muss die Bewegungsgleichung numerisch integrieren oder analytische Lösungen verwenden, die nur unter Näherungsannahmen zu gewinnen sind.
- Der Einschwingvorgang (bei periodischer Anregung) ist nicht durch die Überlagerung der stationären Schwingung mit einer freien Schwingung gegeben.
- Die eingeschwungene stationäre Schwingung ist nicht immer unabhängig von den Anfangsbedingungen.
- Nach Fouriertransformation bleiben die Bewegungsgleichungen für verschiedene Frequenzen miteinander gekoppelt.
Amplitudensprünge[Bearbeiten | Quelltext bearbeiten]
Als Beispiel sei das symmetrische Kraftgesetz (der obige Fall B) untersucht: Die Bewegungsgleichung lautet (nach Division durch , mit sowie ):
Ausgehend von der Annahme einer stationären harmonischen Schwingung
ergibt sich daraus für die verursachende Kraft
- (**) .
Der mit oszillierende Anteil der Kraft rührt von der Umformung her. Dieser Anteil wird im Weiteren vernachlässigt. Die Kraft lässt sich dann näherungsweise zu
zusammenfassen, so dass hier eine mit der Frequenz harmonisch schwingende Kraft eine harmonische Schwingung derselben Frequenz erzeugt. Dabei ist eine Phasenverschiebung und die Amplitude der Kraft durch
gegeben. Diese Gleichung lässt sich zwar nicht in der für die Resonanzkurve üblichen Form umstellen. Jedoch kann man sie nach auflösen und erhält den Zusammenhang zwischen Erregerfrequenz und stationärer Schwingungsamplitude (für die durch gegebene Kraftamplitude) in der Form:
- .
Die beiden Lösungen , die hier durch die Lösung einer quadratischen Gleichung entstehen, drücken aus, dass im Allgemeinen zwei Erregerfrequenzen zu gleich großer Amplitude der stationären Schwingung führen, wie es auch schon beim harmonischen Oszillator links und rechts der Resonanzspitze der Fall ist. Für den harmonischen Fall, , stimmt diese Formel mit der Resonanzkurve der harmonischen erzwungenen Schwingungen überein, die ihr Amplitudenmaximum bei hat und zu beiden Seiten hin symmetrisch abfällt. Neu ist beim anharmonischen Oszillator, dass die Resonanzfrequenz sich mit steigender Amplitude verschiebt (Term in der Formel). Dadurch kann sich im Schaubild der Resonanzkurve die ganze Resonanzspitze derartig krümmen, dass sie in bestimmten Frequenzbereichen eine S-förmige Gestalt annimmt, also trotz gleicher Kraftamplitude und Erregerfrequenz bis zu drei verschiedene mögliche Werte für die stationäre Amplitude anzeigt. Wird bei langsamer, stetiger Variation der Erregerfrequenz solch ein Bereich erreicht, springt die Amplitude von einem Ast der Resonanzkurve auf einen anderen: Die Schwingung „kippt“.
Subharmonische Anregung[Bearbeiten | Quelltext bearbeiten]
Im vorigen Abschnitt wurde ein Beitrag zur Kraft, der mit der Frequenz oszilliert, in der Gleichung (**) einfach weggelassen. Das ist nicht immer gerechtfertigt, denn dieser Beitrag kann bei bestimmten Bedingungen auch die Hauptrolle spielen. Wenn gilt, dass
- sowie ,
dann verschwinden aus Gleichung (**) alle mit periodischen Terme. Es bleibt:
ist eine Lösung zur externen Kraft
- .
Beispiel: Das mathematische Pendel mit Grundfrequenz ( Erdbeschleunigung, Pendellänge), das Kraftgesetz genähert durch Wahl des Parameters , werde angetrieben durch eine externe Kraft
- .
Dann schwingt es mit Amplitude und einer dreifach untersetzten Frequenz wie . Um dies Verhalten beobachten zu können, muss man allerdings entweder die richtigen Anfangsbedingungen treffen oder das Abklingen von zusätzlichen Eigenschwingungen abwarten, was wegen der Annahme einer vernachlässigbar geringen Dämpfung sehr lange dauern kann.
Intermodulation[Bearbeiten | Quelltext bearbeiten]
Mit Intermodulation wird das Phänomen bezeichnet, dass der Oszillator bei Anregung mit zwei Frequenzen mit einer Schwingung antwortet, in der auch Kombinationsfrequenzen ( und ganzzahlig) vertreten sind. Während des Einschwingvorgangs, der aber wegen der Dämpfung gewöhnlich nur kurz dauert, sind solche Frequenzvielfache und Kombinationsfrequenzen auch in Bezug auf die Grundfrequenz vorhanden. In der Akustik können sie als hörbare Töne auftreten, die ihre Ursache darin haben, dass das Trommelfell oder eine Lautsprechermembran über diejenige Auslenkung hinaus erregt wird, bis zu der das lineare Kraftgesetz anwendbar ist.
Literatur[Bearbeiten | Quelltext bearbeiten]
Friedhelm Kuypers: Klassische Mechanik. 8. Auflage. Wiley-VCH, Weinheim 2007, ISBN 978-3-527-40721-7.
Dieter Guicking: Schwingungen (Kap. 5 Nichtlineare und parametrische Systeme). Wiley-VCH, Weinheim 2016, ISBN 978-3-658-14136-3.























































































