Harmonischer Oszillator (Quantenmechanik)
Der harmonische Oszillator in der Quantenmechanik beschreibt, analog zum harmonischen Oszillator in der klassischen Physik, das Verhalten eines Teilchens in einem Potential der Form
- .
- mit Auslenkung, Richtgröße, Masse, Kreisfrequenz
Ein solches quadratisches Potential bezeichnet man auch als harmonisches Potential. Klassisch erhält man dieses Potential für ein System, dessen Rückstellkraft proportional zur Auslenkung aus der Ruhelage ist.
Da ein beliebiges Potential in der Nachbarschaft einer stabilen Gleichgewichtslage oft näherungsweise als harmonisches Potential beschrieben werden kann, ist dies eines der wichtigsten Modellsysteme in der Quantenmechanik. Zudem ist es eines der wenigen quantenmechanischen Systeme, für die eine genaue analytische Lösung bekannt ist.
Hamilton-Operator und Eigenzustände im eindimensionalen Fall[Bearbeiten | Quelltext bearbeiten]
Der Hamilton-Operator oder auch Energieoperator, der in der Quantenmechanik die Gesamtenergie (kinetische Energie + potentielle Energie) beschreibt, ist für den harmonischen Oszillator
Dabei ist die Teilchenmasse und die Eigenkreisfrequenz des Oszillators. In der hier gewählten Ortsdarstellung ist der Ortsoperator und der Impulsoperator . Die quadrierte Ortsableitung ist durch den Laplace-Operator ausgedrückt.
Die stationäre Schrödinger-Gleichung
für den eindimensionalen harmonischen Oszillator lautet damit

Normierbare Lösungen dieser linearen Differentialgleichung ergeben sich nur für die Eigenwerte
- .
Die Lösungsfunktionen, also die Energieeigenfunktionen des harmonischen Oszillators, sind die Hermite-Funktionen (Herleitung z. B. über die Leiteroperatormethode möglich, s. u.):
- .
Die charakteristische Längen-Konstante
wird als Oszillatorlänge bezeichnet und kann als natürliche Längeneinheit genutzt werden. Mit
vereinfacht sich die letzte Formel zu
- .
Dabei sind die Hermite-Polynome:
- oder äquivalent
also
Der Grundzustand hat die Form einer Gauß-Kurve mit der Operatorlänge als Standardabweichung. Er bildet ein Wellenpaket, das nur aus einem Wellenberg besteht und das minimale Produkt aus Orts- und Impulsunschärfe aufweist:
- .
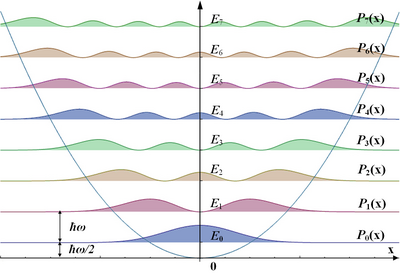
Die nebenstehende obere Grafik zeigt oben die ersten acht Wellenfunktionen , darunter deren Betragsquadrat, das die Aufenthaltswahrscheinlichkeit des Teilchens angibt. Das gegebene harmonische Potential ist die blaue Parabel. Die Höhen der Nulllinien entsprechen den Energieniveaus, so dass ihre Schnittpunkte mit der Potentialkurve die Orte kennzeichnen, an denen ein klassisches Teilchen gleicher Energie umkehren würde. Der schnelle Abfall der Aufenthaltswahrscheinlichkeit im Außenbereich rührt in der Formel für die von dem Faktor her.
Nullpunktenergie[Bearbeiten | Quelltext bearbeiten]
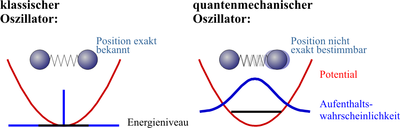
Der Zustand mit der niedrigsten Energie liegt somit über dem Potentialminimum. Dadurch ist das Teilchen in Übereinstimmung mit der heisenbergschen Unschärferelation nicht exakt bei lokalisiert, wie man es von einem klassischen Oszillator erwarten würde. Man spricht hier von einer Nullpunktenergie bzw. Nullpunktsschwingung. In den Quantenfeldtheorien führt dies zu Vakuumfluktuationen.
Die Leiteroperatormethode[Bearbeiten | Quelltext bearbeiten]
Das Problem des harmonischen Oszillators in der Quantenmechanik lässt sich auch mithilfe der Methode der Erzeugungs- und Vernichtungsoperatoren behandeln. Sie wurde von Paul Dirac, basierend auf Arbeiten von Niels Bohr und Otto Wiener, entwickelt und wird auch algebraische Methode genannt.
Für diesen Lösungsweg definiert man den dimensionslosen Operator
Der adjungierte Operator ist dann
Daraus folgt die Darstellung des Ortsoperators und des Impulsoperators durch
- .
Unter Benutzung der kanonischen Vertauschungsrelation kann man den Hamiltonoperator dann durch das Produkt aus und darstellen:
Ebenso ergibt sich die Vertauschungsrelation , mit der man die Operatoridentitäten
- und
zeigen kann.
Angewandt auf einen Energieeigenzustand , ergeben diese Gleichungen, dass ebenfalls ein Energieeigenzustand ist, und zwar zu einer um höheren Energie. Entsprechend ist Eigenzustand zur um niedrigeren Energie. Da die Anwendung dieser Operatoren die Energie des Zustandes um jeweils ein Energiequant verändern, bezeichnet man sie als Leiteroperatoren oder auch als Erzeugungs- und Vernichtungsoperatoren oder als Auf- und Absteigeoperatoren. Da der Operator als Summe von Quadraten hermitescher Operatoren positiv definit ist, ist die Energie nach unten beschränkt. Wiederholte Anwendung des Absteigeoperators auf einen Eigenzustand würde aber zu negativen Eigenwerten der Energie führen, wenn dies nicht an einem Zustand dadurch abbricht, dass gleich dem Nullvektor ist. Dieser ist der Grundzustand, seine Eigenwertgleichung ist
Die Grundzustandsenergie ist also . Der -te angeregte Zustand ergibt sich durch -fache Anwendung des Aufsteigeoperators: . (Der Vorfaktor ergibt sich aus der Forderung, dass die Eigenzustände normiert sein sollen.) Seine Energie ist . Zur Vereinfachung schreibt man die Eigenzustände zur Energie auch einfach als . Aus der Darstellung von folgt, dass die Anwendung des Operators
auf Energieeigenzustände gerade die Zahl , also die Anzahl der Energiequanten ergibt, weswegen er auch Anzahloperator genannt wird.
Eine besonders wichtige Eigenschaft der Kletteroperatoren ist diese:
Statt aus der Schrödingergleichung lässt sich die Wellenfunktion des Grundzustands aus der Gleichung bestimmen, wenn man diese algebraische Gleichung in Ortsdarstellung als Differentialgleichung 1. Ordnung ausdrückt. In der Variable geschrieben, lautet diese Gleichung
und hat die leicht zu findende Lösung
- .
Die Wellenfunktionen der angeregten Zustände erhält man durch -fache Anwendung des Aufsteigeoperators auf .
Diese algebraische Methode ist eine der Grundlagen der zweiten Quantisierung und ebnete den Weg zur Quantenfeldtheorie. Weiteres hierzu ist unter Erzeugungs- und Vernichtungsoperator zu finden.
Harmonische Schwingung eines Wellenpakets und Kohärenter Zustand[Bearbeiten | Quelltext bearbeiten]

Harmonische Schwingung[Bearbeiten | Quelltext bearbeiten]
Setzt man ein Wellenpaket von der Form des Grundzustands zur Zeit mit dem Mittelpunkt an eine Stelle , dann ist dessen Wellenfunktion durch
gegeben.[1] Beim Einsetzen in die Schrödingergleichung zeigt sich, dass dieses Wellenpaket ohne Formänderung in dem Parabelpotential eine harmonische Schwingung mit der Amplitude und der Frequenz ausführt (siehe Abbildung von oben nach unten). Es verhält sich exakt wie ein klassisches Teilchen mit der Energie
- ,
die auch klassisch zu den Anfangsbedingungen (bei ) gehört. Zu jedem Zeitpunkt erfüllen die Erwartungswerte und von Ort und Impuls die Energieerhaltung
- .
Gibt man dem Wellenpaket einen Anfangsimpuls , dann heißt die Wellenfunktion
und schwingt exakt wie ein klassisches Teilchen mit der Energie
- ,
die auch klassisch zu den Anfangsbedingungen gehört. Die Amplitude ist die Auslenkung am Umkehrpunkt beim Impuls Null und ergibt sich aus
- .
Die Wellenfunktion kann als Linearkombination der (normierten) Energie-Eigenfunktionen dargestellt werden:
- .
Wenn die Anfangsbedingungen in einer dimensionslosen komplexen Zahl zusammengefasst werden:
ergeben sich die Koeffizienten in Abhängigkeit von
- .
Diese Entwicklung folgt aus der Gleichung für die Erzeugende Funktion der Hermite-Polynome, wenn man diese mithilfe der oben angegebenen Formel für die Eigenfunktionen ausdrückt. Für , klassisch also die Ruhelage, verschwinden alle Amplituden bis auf , für kommt richtig der Grundzustand heraus.
Die einzelnen Energieeigenzustände sind demnach mit den Gewichten
vertreten, worin der Parameter die klassische Energie in Einheiten der Energiequanten angibt. Diese Formel gibt eine Poisson-Verteilung wieder, die ihr Maximum bei den Zahlen hat, also denjenigen Quantenzahlen, die der klassischen Energie entsprechen. Die relative Standardabweichung um das Maximum ist und damit bei klassischen Systemen unbeobachtbar klein. Der quantenmechanische Erwartungswert der Energie ist
Das zeitliche Verhalten der Wellenfunktion erhält man, wenn jede Energieeigenfunktion mit ihrer Zeithabhängigkeit eingesetzt wird:
- .
Dadurch ergeben sich ein gemeinsamer Phasenfaktor und veränderte Koeffizienten
- .
Der Zustand zu einer beliebigen Zeit sieht also genau so aus wie das Wellenpaket zur Zeit , nur mit veränderter Anfangsbedingung . Deren Veränderung ist eine Rotation in der komplexen Ebene, also ein harmonisches Oszillieren von Real- und Imaginärteil, d. h von Ort und Impuls.
Historische Anmerkung: Als Erwin Schrödinger im Frühjahr 1926 die Wellenmechanik entwickelte, stieß er schon früh auf dieses Beispiel für quasiklassisches Verhalten eines Wellenpakets.[2] Er knüpfte daran die schließlich vergebliche Hoffnung, Teilchen generell als Wellenpakete ansehen zu können und somit die Quantenmechanik letztlich zu einem Zweig der klassischen Physik zu machen.[3]
Kohärenter Zustand[Bearbeiten | Quelltext bearbeiten]
Der Zustand des oszillierenden Wellenpakets wird als kohärenter Zustand oder quasiklassischer Zustand bezeichnet und meist so geschrieben:
Er ist Eigenzustand zum (nicht hermiteschen) Absteigeoperator mit dem (komplexen) Eigenwert :
Die zeitliche Entwicklung des Zustands ist wegen
dadurch gegeben, dass der Parameter durch ersetzt wird und der Zustand mit dem (von unabhängigen, also hier unerheblichen) Phasenfaktor multipliziert wird:
- .
Der Parameter läuft demnach in der komplexen Ebene auf einem Kreis um den Ursprung, so dass sein Realteil und sein Imaginärteil mit der Kreisfrequenz um phasenversetzt harmonisch oszillieren. Der Zustand hat die gleiche Gestalt wie bei , nur mit anderen Anfangsbedingungen , deren zeitliches Verhalten eine harmonische Schwingung beschreibt.
Wichtig sind solche Zustände bei der Beschreibung von kohärenter Strahlung, da man zeigen kann, dass sich das Lichtfeld in der Quantenfeldtheorie auf harmonische Oszillatoren (einer für jede Mode des Feldes) zurückführen lässt (siehe auch kohärente Strahlung).
Experiment[Bearbeiten | Quelltext bearbeiten]
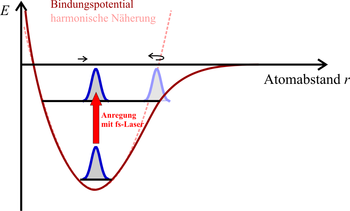
In Experimenten kann in einem zweiatomigen Molekül (z. B. Wasserstoff H2), also einem Quantensystem, ein Zustand erzeugt werden, der diesem quasiklassischen Zustand nahekommt. Oben wurde bereits erläutert, dass man für die Schwingung der Kerne zweiatomiger Moleküle den harmonischen Oszillator als Näherung verwenden kann. Dazu regt man das Molekül mit Hilfe eines intensiven Femtosekundenlasers an.[4] In der folgenden Abbildung ist das Geschehen schematisch gezeigt: Zunächst wird mit einem Laserpuls eine tiefliegende schmale Wellenfunktion in einen höheren Energiezustand angehoben. Dort bleibt sie weiter lokalisiert und beginnt sich als quasiklassischer Zustand im Potential zu bewegen, d. h. die beiden Kerne führen (näherungsweise) harmonische Schwingungen gegeneinander aus. Zur Messung wird dann ein zweiter Puls mit einer Quantenenergie eingestrahlt, die bei genügend großem Abstand der Kerne gerade zur Spaltung des Moleküls ausreicht. Die Bruchstücke werden nachgewiesen, aus ihrer kinetischen Energie kann auf den Abstand bei der Spaltung und damit auf die genauere Form des Potentials geschlossen werden.
Klassischer Grenzfall[Bearbeiten | Quelltext bearbeiten]
Die zeitabhängigen Energieeigenfunktionen gehören zu stationären Zuständen und lassen nichts von einer harmonischen Schwingung erkennen. Jedoch geht die Aufenthaltswahrscheinlichkeit Im Grenzfall großer Quantenzahlen in die klassische Aufenthaltswahrscheinlichkeit über. Diese klassische Wahrscheinlichkeitsdichte ist proportional zur inversen Geschwindigkeit . Je kleiner die Geschwindigkeit des klassischen Teilchens im Potential ist, desto länger verweilt es an einem entsprechenden Ort. Die Geschwindigkeit an jedem Ort kann man direkt aus dem Energiesatz ableiten. Die folgende Abbildung zeigt die klassische und die quantenmechanische Aufenthaltswahrscheinlichkeitsdichte. Je größer wird, desto ähnlicher werden sich die Kurven:

N-dimensionaler harmonischer Oszillator[Bearbeiten | Quelltext bearbeiten]
Der eindimensionale harmonische Oszillator kann leicht auf den N-dimensionalen Fall erweitert werden. Der Hamilton-Operator in Dimensionen ist
- .
Daraus wird deutlich, dass der N-dimensionale harmonische Oszillator genau unabhängigen eindimensionalen harmonischen Oszillatoren mit der gleichen Masse und Rückstellkraft entspricht, denn eine Summe aus unabhängigen Eigenfunktionen für jede Koordinate nach dem obigen eindimensionalen Schema löst die Schrödingergleichung. Dies ist eine vorteilhafte Eigenschaft des Potentials (vgl. Satz des Pythagoras), welches es ermöglicht die potentielle Energie in Terme zu trennen, die nur von jeweils einer Koordinate abhängen.
Die möglichen Energieniveaus ergeben sich entsprechend zu
- .
Zu beachten ist jedoch, dass die Energieniveaus des N-dimensionalen Oszillators entsprechend der kombinatorischen Möglichkeiten zur Realisierung der Niveaus entartet sind. Der Entartungsgrad ergibt sich aus dem Binomialkoeffizienten:
Diese Entartung ist nicht zufällig, sondern beruht zum Teil auf der Rotationssymmetrie des Systems. Rotationssymmetrie hat ganz allgemein zur Folge, dass Energieeigenzustände auch als Drehimpulseigenzustände gewählt werden können, deren Energien hinsichtlich der magnetischen Quantenzahl entartet sind. Speziell beim quadratischen Potential des Oszillators sind darüber hinaus auch Zustände mit geraden Drehimpulsquantenzahlen miteinander entartet, ebenso die mit ungeraden.
Gekoppelte harmonische Oszillatoren[Bearbeiten | Quelltext bearbeiten]
Betrachtet man im einfachsten Fall ein System aus zwei eindimensionalen Teilchen, welche nur durch eine harmonische Kraft aneinandergekoppelt sind, so ergibt sich dafür der Hamilton-Operator
Da eine einfache Separation der Schrödingergleichung zunächst verhindert, bietet sich eine Transformation in Schwerpunkt-Koordinaten an:
Die Impulse lassen sich durch die Impulse der Schwerpunktkoordinaten ausdrücken als
- .
Damit gelingt die Separation des Hamiltonoperators
Dies entspricht einem einzelnen harmonischen Oszillator bzgl. der Differenzschwingung der 2 Teilchen (mit doppelter reduzierter Masse), wobei sich das System als Ganzes zusätzlich wie ein freies Teilchen bewegt. Die Lösung der Schrödingergleichung führt entsprechend zu den harmonischen Energieniveaus
- .
Bei einer Kette aus derart paarweise harmonisch hintereinander gekoppelter Teilchen (eindimensionales Gitter) findet man ähnlich eine Koordinatentransformation derart, dass voneinander unabhängige kollektive harmonische Schwingungen (plus eine kommunale Schwerpunktsbewegung) resultieren.[5]
Bei dreidimensionalen Kristallgittern in der Festkörperphysik führt diese Betrachtung dann zu den Phononen.
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Der harmonische Oszillator ist ein wichtiges Modellsystem der Quantenphysik, da es eines der wenigen geschlossen (also ohne Näherungen und numerische Methoden) lösbaren Systeme der Quantenmechanik ist. Mit ihm können eine Reihe physikalischer Sachverhalte näherungsweise beschrieben werden:
- In der Molekülphysik erlaubt er eine Näherung der Bindungsverhältnisse zwischen Atomen und ermöglicht so z. B. eine Vorhersage über Schwingungsspektren. Dies lässt sich verdeutlichen, indem eine Bindung durch zwei über eine Feder (harmonisches Potential) miteinander verbundene Massepunkte (die Atome), die gegeneinander schwingen, dargestellt wird:

- Die lineare Rückstellkraft einer solchen Feder führt auf ein harmonisches Potential (proportional ) und somit auf den harmonischen Oszillator. In realen Molekülen sieht das Potential etwas anders aus (vergleiche Morse-Potential), aber der harmonische Oszillator ist, zumindest für niedrige Schwingungsenergien, eine gute Näherung.
- Ein weiteres Beispiel ist die Torsionsschwingung des Ethenmoleküls, die in der folgenden Zeichnung dargestellt ist:
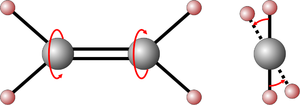
- Dabei verdrillt sich sozusagen die Doppelbindung und jeweils zwei Wasserstoff-Atome schwingen drehend gegeneinander.
- In der modernen Atomphysik werden zu untersuchende Atome und Ionen in optischen Fallen bzw. Ionenfallen gefangen und gekühlt, um z. B. bei Messungen eine höhere Auflösung zu erhalten. Außerdem kann man in solchen Fallen neue Zustände der Materie untersuchen (z. B. Bose-Einstein-Kondensate, Fermi-Kondensate). Solche Fallen weisen ein, in erster Näherung, parabolisches Potential auf. Somit können Teilchen in diesen Fallen ebenfalls mit dem Modell des quantenmechanischen harmonischen Oszillators beschrieben werden.
- In der Festkörperphysik beschreibt das Einstein-Modell (nach Albert Einstein) eine Methode, um den Beitrag der Gitterschwingungen (Phononen) zur Wärmekapazität eines kristallinen Festkörpers zu berechnen. Grundlage ist die Beschreibung des Festkörpers als aus N quantenharmonischen Oszillatoren bestehend, die jeweils in drei Richtungen unabhängig schwingen können. Außerdem können Phononen auch durch eine Ansammlung gekoppelter harmonischer Oszillatoren beschrieben werden. Dabei ist jedes Atom im Kristallgitter ein Oszillator, der an seine Nachbaratome gekoppelt ist.
Quellen[Bearbeiten | Quelltext bearbeiten]
- Claude Cohen-Tannoudji, Bernard Diu, Franck Laloë, Franck: Quantenmechanik 1/2., 2. Auflage, Walter de Gruyter, Berlin – New York 1999
- Jun John Sakurai: Modern Quantum Mechanics. Addison-Wesley
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Vollständige Lösung des harmonischen Oszillators mit Hilfe der algebraischen Methode (ab Seite 63; PDF-Datei; 4,26 MB)
- Darstellung der direkten Lösung des harmonischen Oszillators in der Ortsdarstellung
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Albert Messiah: Quantum Mechanics Bd. I. North Holland Publ. Comp, Amsterdam 1970, S. 446–448.
- ↑ Erwin Schrödinger: Der stetige Übergang von der Mikro-zur Makromechanik. In: Naturwissenschaften. Band 14, Nr. 28, 1926, S. 664–666.
- ↑ Abraham Pais: Inward bound: of matter and forces in the physical world. Clarendon Press, Oxford 1994, ISBN 0-19-851971-0, S. 256.
- ↑ Th. Ergler, A. Rudenko, B. Feuerstein, et al.: Time-Resolved Imaging and Manipulation of H2 Fragmentation Intense Laser Fields In: Phys. Rev. Lett. 95, 093001, 2005
- ↑ Armstrong, Zinner, Fedorov, Jensen: Analytic Harmonic Approach to the N-body problem. In: Journal of Physics B: Atomic, Molecular and Optical Physics. 44. Jahrgang, Nr. 5, 2011, S. 055303, doi:10.1088/0953-4075/44/5/055303, arxiv:1011.2453v2, bibcode:2011JPhB...44e5303A.































![{\displaystyle [{\hat {p}},{\hat {x}}]=-i\hbar }](https://wikimedia.org/api/rest_v1/media/math/render/svg/36b760e28a76f90a593f3ca2d88da979317e622c)



![{\displaystyle [{\hat {a}},{\hat {a}}^{\dagger }]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b409c0a062d7915ff0b9eb45430b383ae9926ec)






















![{\displaystyle \left[y+{\frac {\partial }{\partial y}}\right]\psi _{0}(y)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1467710b1dfaf5a49f5c4d792677e97528c02548)








































![{\displaystyle \alpha \ [=\alpha _{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bacf7cbd61681054b7bbe5ff2441163df32ac2e)










![{\displaystyle E_{n}=\hbar \omega \left[(n_{1}+\cdots +n_{N})+{\frac {N}{2}}\right]=\hbar \omega \left[n+{\frac {N}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d2aca6e8aeec4a2e2a1d39a22083c4631296e3)















