CG-Verfahren
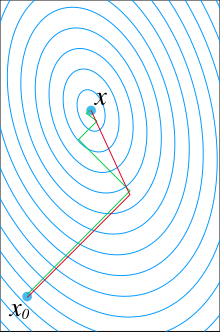
Das CG-Verfahren (von engl. conjugate gradients oder auch Verfahren der konjugierten Gradienten) ist eine effiziente numerische Methode zur Lösung von großen linearen Gleichungssystemen der Form mit symmetrischer, positiv definiter Systemmatrix .
Das Verfahren liefert, in exakter Arithmetik, nach spätestens Schritten die exakte Lösung, wobei die Größe der quadratischen Matrix ist. Insbesondere ist es aber als iteratives Verfahren interessant, da der Fehler monoton fällt. Das CG-Verfahren kann in die Klasse der Krylow-Unterraum-Verfahren eingeordnet werden.
Es wurde zuerst 1952 von Eduard Stiefel und Magnus Hestenes vorgeschlagen.[1] Ein für bestimmte Gleichungssysteme äquivalentes Verfahren schlug auch Cornelius Lanczos Anfang der 1950er Jahre mit dem Lanczos-Verfahren vor.
Idee des CG-Verfahrens[Bearbeiten | Quelltext bearbeiten]
Die Idee des CG-Verfahrens besteht darin, dass für symmetrisches und positiv definites das Minimieren der quadratischen Form
äquivalent zum Lösen von ist. Hierbei bezeichnet das Standardskalarprodukt.
Der Gradient von an der Stelle ist gerade und somit bei großen, dünn besetzten Matrizen schnell zu berechnen. Die Idee des CG-Verfahrens ist es nun, anstelle in Richtung des Residuums wie beim Gradientenverfahren in eine andere Richtung die Funktion über einen Unterraum zu minimieren. Die Richtungen sind dabei alle -konjugiert, das heißt, es gilt
- .
Die Iterierten des CG-Verfahrens werden dann so gewählt, dass sie das Minimum von in dem affinen Raum , der durch die Vektoren aufgespannt und um verschoben wird, bilden:
Es lässt sich zeigen, dass ebenfalls gilt:
Der letzte Teil zeigt, dass die Suchrichtungen den Krylowraum zu A und aufspannen. Das CG-Verfahren lässt sich deswegen alternativ direkt als Krylow-Unterraum-Verfahren definieren.
Da die Vektoren alle -konjugiert sind, ist die Dimension von gerade , falls die Vektoren sind. Man kann zeigen, dass ist, wenn ist. Ist also eine -Matrix, so terminiert das Verfahren nach spätestens Schritten, falls exakt gerechnet wird. Numerische Fehler können durch weitere Iterationen eliminiert werden. Hierzu betrachtet man den Gradienten , der das Residuum angibt. Unterschreitet die Norm dieses Residuums einen gewissen Schwellenwert, wird das Verfahren abgebrochen.
Das Verfahren baut sukzessive eine -orthogonale Basis für den auf und minimiert in die jeweilige Richtung bestmöglich.
Das Problem bei dem iterativen Verfahren ist das Finden der optimalen Schrittweite. Um die Güte eines Punktes zu bestimmen ist jeweils eine vollständige Matrixmultiplikation notwendig, welche nebenbei gleich einen neuen Gradienten liefert. Ist die Schrittweite entlang eines vorgegebenen Gradienten zu ungenau, entspricht die Methode eher einem einfachen Bergsteigeralgorithmus.
CG-Verfahren ohne Vorkonditionierung[Bearbeiten | Quelltext bearbeiten]
Zunächst wählt man ein beliebig und berechnet:
Für führt man aus:
- Speichere Matrix-Vektor-Produkt, um es nur einmal auszurechnen
- Finde von in Richtung den Ort des Minimums der Funktion und aktualisiere den Gradienten bzw. das Residuum
- Korrigiere die Suchrichtung mit Hilfe von und
bis das Residuum in der A-Norm kleiner als eine Toleranz ist ().
Varianten[Bearbeiten | Quelltext bearbeiten]
Es existieren verschiedene Varianten des Verfahrens, neben der ersten von Roger Fletcher und Colin Reeves z. B. von Magnus Hestenes und Eduard Stiefel, von William Davidon, Fletcher und Michael J. D. Powell oder von Elijah Polak und Gerard Ribière. Diese sind für quadratische Formen (wie oben definiert) identisch, da die weiteren Terme aufgrund der Orthogonalität der Residuen verschwinden. Verwendet man das CG-Verfahren aber, um eine durch eine quadratische Form angenäherte Funktion zu minimieren, so zeigen diese Varianten oft besseres Konvergenzverhalten als die ursprüngliche Formulierung von Fletcher und Reeves.
- (Fletcher-Reeves)
- (Polak-Ribière)
- (Hestenes-Stiefel)
CG-Verfahren mit symmetrischer Vorkonditionierung (PCG-Verfahren)[Bearbeiten | Quelltext bearbeiten]
Die Konvergenz des CG-Verfahrens ist nur bei symmetrischen positiv definiten Matrizen gesichert. Dies muss ein Vorkonditionierer berücksichtigen. Bei einer symmetrischen Vorkonditionierung wird das Gleichungssystem mit Hilfe einer Vorkonditionierer-Matrix zu mit transformiert, und darauf das CG-Verfahren angewandt.
Die Matrix ist symmetrisch, da symmetrisch ist. Sie ist ferner positiv definit, da nach dem Trägheitssatz von Sylvester und die gleichen Anzahlen positiver und negativer Eigenwerte besitzen.
Das resultierende Verfahren ist das sogenannte PCG-Verfahren (von engl. Preconditioned Conjugate Gradient):
Zunächst wählt man ein beliebig und berechnet:
Für setzt man:
- Speichere Matrix-Vektor-Produkt, um es nur einmal auszurechnen
- Finde von in Richtung das Minimum und aktualisiere Gradienten und vorkonditionierten Gradienten
- (Residuum)
- Korrigiere die Suchrichtung
bis das Residuum in der Norm kleiner als eine Toleranz ist ().

Ein häufiger Vorkonditionierer im Zusammenhang mit CG ist die unvollständige Cholesky-Zerlegung. Diese Kombination wird auch als ICCG bezeichnet und wurde in den 1970ern von Meijerink und van der Vorst eingeführt.
Zwei weitere für das PCG-Verfahren zulässige Vorkonditionierer sind der Jacobi-Vorkonditionierer , wobei die Hauptdiagonale von ist, und der SSOR-Vorkonditionierer
mit , wobei die Hauptdiagonale und die strikte untere Dreiecksmatrix von ist.
Konvergenzrate des CG-Verfahrens[Bearbeiten | Quelltext bearbeiten]
Man kann zeigen, dass die Konvergenzgeschwindigkeit des CG-Verfahrens durch
beschrieben wird. Hierbei ist die Kondition der Matrix bezüglich der Spektralnorm, also der von der euklidischen Norm erzeugten Matrixnorm, sowie die Energienorm von . Der Ausdruck ist nicht negativ, da die Konditionszahl (bzgl. einer von einer Vektornorm erzeugten Matrixnorm) einer Matrix immer größer oder gleich 1 ist. Da symmetrisch und positiv definit ist, gilt
- .
Aus der Minimierungseigenschaft lässt sich ferner herleiten, dass
- ,
wobei ein beliebiges Polynom vom Grad ist mit und die Lösung. Mit ist das Spektrum, also die Menge der Eigenwerte der Matrix gemeint. Daraus folgt, dass das CG-Verfahren ein System zu einer Matrix mit nur verschiedenen Eigenwerten in Schritten löst und dass das CG-Verfahren für Systeme, bei denen die Eigenwerte in wenigen kleinen Umgebungen konzentriert sind, sehr schnell konvergiert. Dies wiederum liefert einen Anhaltspunkt für sinnvolle Vorkonditionierer: Ein Vorkonditionierer ist dann gut, wenn er dafür sorgt, dass die Eigenwerte konzentriert werden.
Erweiterung auf unsymmetrische Matrizen[Bearbeiten | Quelltext bearbeiten]
Ist die Systemmatrix A unsymmetrisch, aber regulär, so kann das CG-Verfahren auf die Normalgleichungen
angewendet werden, da für eine reguläre Matrix A symmetrisch und positiv definit ist. Dieses Verfahren nennt sich auch CGNR (von engl. Conjugate Gradients Normal Residual), da bei diesem Vorgehen die Norm des Residuums von minimiert wird. Alternativ gibt es das Verfahren CGNE (von engl. Conjugate Gradient Method on the Normal Equations), welches
löst mit . Hierbei wird der Fehler minimiert.
Beide Verfahren haben den Nachteil, dass zum einen zur Verfügung stehen muss, was nicht immer gegeben ist, und zum anderen die Kondition von A bei diesem Ansatz quadriert wird, was zur Verlangsamung der Konvergenz führen kann.
Literatur[Bearbeiten | Quelltext bearbeiten]
- C. T. Kelley: Iterative Methods for Linear and Nonlinear Equations. SIAM, ISBN 0-89871-352-8. (PDF; 783 kB)
- P. Knabner, L. Angermann: Numerik partieller Differentialgleichungen. Springer, ISBN 3-540-66231-6.
- A. Meister: Numerik linearer Gleichungssysteme. Vieweg, 1999, ISBN 3-528-03135-2.
- H. William, Saul A. Teukolsky: Numerical Recipes in C++. Cambridge University Press, 2002, ISBN 0-521-75033-4.
- J. R. Shewchuck: An Introduction to the Conjugate Gradient Method Without the Agonizing Pain. (PDF; 503 kB).
- Eduard Stiefel: Über einige Methoden der Relaxationsrechnung. In: Zeitschrift für angewandte Mathematik und Physik. Band 3, Nr. 1, 1952, S. 1–33.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ M. R. Hestenes, E. Stiefel: Methods of conjugate gradients for solving linear systems. In: Journal of Research of the National Bureau of Standards. Bd. 49, 1952, S. 409–436. doi:10.6028/jres.049.044






























![{\displaystyle {\begin{aligned}\alpha _{k}\;&=\;{\frac {r_{k}^{T}r_{k}}{d_{k}^{T}\,z}},\\[.2em]x_{k+1}\;&=\;x_{k}+\alpha _{k}d_{k},\\[.4em]r_{k+1}\;&=\;r_{k}-\alpha _{k}z\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f2dfa3155ee358d08f8e3c9d56dc22bd44bc670)


![{\displaystyle {\begin{aligned}\beta _{k}\;&=\;{\frac {r_{k+1}^{T}r_{k+1}}{r_{k}^{T}r_{k}}},\\[.2em]d_{k+1}\;&=\;r_{k+1}+\beta _{k}d_{k},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9358596176e5349ae1fb5a3feb950d247ea2ed16)





















![{\displaystyle C=\left[{\tfrac {1}{2-\omega }}\left({\tfrac {1}{\omega }}D+L\right)\left({\tfrac {1}{\omega }}D\right)^{-1}\left({\tfrac {1}{\omega }}D+L\right)^{T}\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc3222086d7cf28ddb44e5f539a5aadbe85bff7)

















