Matrizenmultiplikation
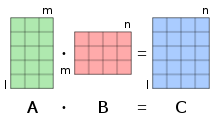
Die Matrizenmultiplikation oder Matrixmultiplikation ist in der Mathematik eine multiplikative Verknüpfung von Matrizen. Um zwei Matrizen miteinander multiplizieren zu können, muss die Spaltenzahl der ersten Matrix mit der Zeilenzahl der zweiten Matrix übereinstimmen. Das Ergebnis einer Matrizenmultiplikation wird dann Matrizenprodukt, Matrixprodukt oder Produktmatrix genannt. Das Matrizenprodukt ist wieder eine Matrix, deren Einträge durch komponentenweise Multiplikation und Summation der Einträge der entsprechenden Zeile der ersten Matrix mit der entsprechenden Spalte der zweiten Matrix ermittelt werden.
Die Matrizenmultiplikation ist assoziativ und mit der Matrizenaddition distributiv. Sie ist jedoch nicht kommutativ, das heißt, die Reihenfolge der Matrizen darf bei der Produktbildung im Allgemeinen nicht vertauscht werden. Die Menge der quadratischen Matrizen mit Elementen aus einem Ring bildet zusammen mit der Matrizenaddition und der Matrizenmultiplikation den Ring der quadratischen Matrizen. Weiter bildet die Menge der regulären Matrizen über einem unitären Ring mit der Matrizenmultiplikation die allgemeine lineare Gruppe. Matrizen, die durch spezielle Multiplikationen mit regulären Matrizen ineinander überführt werden können, bilden darin Äquivalenzklassen.
Der Standardalgorithmus zur Multiplikation zweier quadratischer Matrizen weist eine kubische Laufzeit auf. Zwar lässt sich der asymptotische Aufwand mit Hilfe spezieller Algorithmen verringern, die Ermittlung optimaler oberer und unterer Komplexitätsschranken für die Matrizenmultiplikation ist jedoch noch Gegenstand aktueller Forschung.
Die Matrizenmultiplikation wird häufig in der linearen Algebra verwendet. So wird beispielsweise die Faktorisierung einer Matrix als Produkt von Matrizen mit speziellen Eigenschaften bei der numerischen Lösung linearer Gleichungssysteme oder Eigenwertprobleme eingesetzt. Weiterhin ist die Abbildungsmatrix der Hintereinanderausführung zweier linearer Abbildungen gerade das Matrizenprodukt der Abbildungsmatrizen dieser Abbildungen. Anwendungen der Matrizenmultiplikation finden sich unter anderem in der Informatik, der Physik und der Ökonomie.
Die Matrizenmultiplikation wurde erstmals von dem französischen Mathematiker Jacques Philippe Marie Binet im Jahr 1812 beschrieben.[1]
Definition[Bearbeiten | Quelltext bearbeiten]
Die Matrizenmultiplikation ist eine binäre Verknüpfung auf der Menge der Matrizen über einem Ring (oft der Körper der reellen Zahlen), also eine Abbildung
- ,
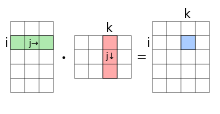
die zwei Matrizen und eine weitere Matrix zuordnet. Die Matrizenmultiplikation ist dabei nur für den Fall definiert, dass die Spaltenzahl der Matrix mit der Zeilenzahl der Matrix übereinstimmt. Die Zeilenzahl der Ergebnismatrix entspricht dann derjenigen der Matrix und ihre Spaltenzahl derjenigen der Matrix . Jeder Eintrag des Matrizenprodukts berechnet sich dabei über
- ,
also durch komponentenweise Multiplikation der Einträge der -ten Zeile von mit der -ten Spalte von und durch Summation all dieser Produkte. Häufig wird bei der Notation einer Matrizenmultiplikation der Malpunkt weggelassen und man schreibt kurz statt . Soll die Reihenfolge der Faktoren betont werden, spricht man „A wird von links mit B multipliziert“ für das Produkt und „A wird von rechts mit B multipliziert“ für das Produkt .
Beispiel[Bearbeiten | Quelltext bearbeiten]
Gegeben seien die beiden reellen Matrizen
- und .
Da die Matrix ebenso viele Spalten wie die Matrix Zeilen besitzt, ist die Matrizenmultiplikation durchführbar. Nachdem zwei Zeilen und zwei Spalten hat, wird das Matrizenprodukt ebenfalls zwei Zeilen und Spalten aufweisen. Zur Berechnung des ersten Matrixelements der Ergebnismatrix werden die Produkte der entsprechenden Einträge der ersten Zeile von und der ersten Spalte von aufsummiert (die Sternchen stehen für noch nicht berechnete Elemente):
Für das nächste Element der Ergebnismatrix in der ersten Zeile und zweiten Spalte wird entsprechend die erste Zeile von und die zweite Spalte von verwendet:
Dieses Rechenschema setzt sich nun in der zweiten Zeile und ersten Spalte fort:
Es wiederholt sich bei dem letzten Element in der zweiten Zeile und zweiten Spalte:
Das Ergebnis ist das Matrizenprodukt . Eine optische Hilfestellung und Unterstützung zur Berechnung des Matrizenprodukts bietet das falksche Schema.[2]

Spezialfälle[Bearbeiten | Quelltext bearbeiten]
Zeilenvektor mal Spaltenvektor[Bearbeiten | Quelltext bearbeiten]
Besteht die erste Matrix aus nur einer Zeile und die zweite Matrix aus nur einer Spalte, so ergibt das Matrizenprodukt eine -Matrix. Interpretiert man eine einzeilige Matrix als Zeilenvektor und eine einspaltige Matrix als Spaltenvektor , so erhält man im Fall reeller Vektoren das Standardskalarprodukt
zweier Vektoren, wobei den zu transponierten Vektor darstellt, beide Vektoren gleich lang sein müssen und das Ergebnis dann eine reelle Zahl ist. Jeder Eintrag eines Matrizenprodukts kann somit als Skalarprodukt eines Zeilenvektors der Matrix mit einem Spaltenvektor der Matrix angesehen werden.

Spaltenvektor mal Zeilenvektor[Bearbeiten | Quelltext bearbeiten]
Besteht umgekehrt die erste Matrix aus nur einer Spalte der Länge und die zweite Matrix aus nur einer Zeile der Länge , so ergibt das Matrizenprodukt eine -Matrix. Wird wieder eine einspaltige Matrix als Spaltenvektor und eine einzeilige Matrix als Zeilenvektor interpretiert, so wird das entstehende Produkt von Vektoren als dyadisches Produkt
bezeichnet. Jeder Eintrag der resultierenden Matrix ist dabei das Produkt eines Elements des ersten Vektors mit einem Element des zweiten Vektors. Das Matrizenprodukt kann so als Summe dyadischer Produkte der Spaltenvektoren von mit den jeweiligen Zeilenvektoren von geschrieben werden.

Matrix mal Vektor[Bearbeiten | Quelltext bearbeiten]
Ein wichtiger Spezialfall einer Matrizenmultiplikation entsteht, wenn die zweite Matrix aus nur einer Spalte besteht. Das Ergebnis der Matrizenmultiplikation ist dann ebenfalls eine einspaltige Matrix. Wird wieder eine einspaltige Matrix als Spaltenvektor interpretiert, so erhält man das Matrix-Vektor-Produkt
- ,
wobei , und sind. Das Matrix-Vektor-Produkt wird beispielsweise in der Matrixschreibweise linearer Gleichungssysteme verwendet.
Eine alternative Darstellung der Matrixmultiplikation ergibt sich durch Umschreiben der Definition. Wir schreiben sodass die die Spalten der Matrix darstellen (unten verdeutlicht durch ). Ist nun dann kann man das Matrix-Vektor-Produkt auch wie folgt lesen:

Das Matrix-Vektor-Produkt ist also eine Linearkombination der Spalten von . Diese Beobachtung lässt sich auch auf ein allgemeines Matrix-Matrix-Produkt übertragen. Ist man am Bild der von der Matrix induzierten linearen Abbildung interessiert, ist diese Darstellung meist intuitiver für weitere Argumentation.
Vektor mal Matrix[Bearbeiten | Quelltext bearbeiten]
Besteht umgekehrt die erste Matrix aus nur einer Zeile, so ergibt das Vektor-Matrix-Produkt
aus einem Zeilenvektor und einer Matrix wieder einen Zeilenvektor . Dieses lässt sich als eine Linearkombination der Zeilen von interpretieren.
Quadrat einer Matrix[Bearbeiten | Quelltext bearbeiten]
Durch Multiplikation einer quadratischen Matrix mit sich selbst ergibt sich wieder eine Matrix gleicher Größe, die als das Quadrat der Matrix bezeichnet wird, das heißt:
Entsprechend dazu wird mit die Matrixpotenz, also das -fache Produkt einer Matrix mit sich selbst, bezeichnet. Matrixpotenzen werden beispielsweise zur Definition des Matrixexponentials und des Matrixlogarithmus verwendet. Umgekehrt heißt eine quadratische Matrix , für die
gilt, Quadratwurzel der Matrix . Eine Matrix kann mehrere, sogar unendlich viele, Quadratwurzeln besitzen. Analog wird eine Matrix, deren -te Potenz die Matrix ergibt, als -te Wurzel dieser Matrix bezeichnet.
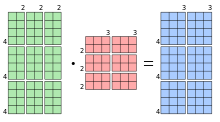
Blockmatrizen[Bearbeiten | Quelltext bearbeiten]
Weisen die beiden Matrizen und eine Blockstruktur auf, wobei die Blockbreiten der ersten Matrix mit den Blockhöhen der zweiten Matrix übereinstimmen müssen, so lässt sich auch das Matrizenprodukt blockweise notieren. Die Ergebnismatrix besitzt dann die Blockhöhen der ersten und die Blockbreiten der zweiten Matrix. Im Fall zweier Matrizen mit je zwei mal zwei Blöcken ergibt sich beispielsweise
- ,
womit die Ergebnismatrix auch zwei mal zwei Blöcke besitzt.

Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Assoziativität[Bearbeiten | Quelltext bearbeiten]
Die Matrizenmultiplikation ist assoziativ, das heißt, für Matrizen , und gilt:
Bei der Multiplikation mehrerer Matrizen ist es also unerheblich, in welcher Reihenfolge die Teilprodukte gebildet werden, solange die Gesamtreihung nicht verändert wird. Für den Eintrag an der Stelle des resultierenden Matrizenprodukts gilt nämlich:
Die Matrizenmultiplikation ist auch verträglich mit der Multiplikation mit Skalaren , das heißt:
Distributivität[Bearbeiten | Quelltext bearbeiten]
Betrachtet man neben der Matrizenmultiplikation auch noch die komponentenweise Matrizenaddition zweier Matrizen , dann sind auch die Distributivgesetze erfüllt. Das heißt, für alle Matrizen gilt
und für alle Matrizen entsprechend
- .
Die Distributivgesetze folgen direkt aus der Distributivität der Addition mit der Multiplikation im Ring über
für das erste Distributivgesetz und über eine analoge Umformung auch für das zweite Distributivgesetz.
Nichtkommutativität[Bearbeiten | Quelltext bearbeiten]
Das Kommutativgesetz hingegen gilt für die Matrizenmultiplikation nicht, das heißt, für und ist im Allgemeinen
- .
Für die beiden Matrizenprodukte gilt nämlich und , womit sie für schon von den Dimensionen her nicht übereinstimmen können. Aber selbst, wenn und quadratisch sind, müssen die beiden Matrizenprodukte nicht gleich sein, wie das Gegenbeispiel
zeigt. Die Nichtkommutativität der Matrizenmultiplikation gilt demnach sogar, wenn die Multiplikation im Ring kommutativ sein sollte, wie es beispielsweise bei Zahlen der Fall ist. Für spezielle Matrizen kann die Matrizenmultiplikation dennoch kommutativ sein, siehe die nachfolgenden Abschnitte.
Weitere Rechenregeln[Bearbeiten | Quelltext bearbeiten]
Für die Transponierte eines Matrizenprodukts gilt:
- .
Die Reihenfolge bei der Multiplikation wird durch die Transposition also vertauscht. Für die Adjungierte des Produkts komplexer Matrizen gilt entsprechend
- .
Die Spur des Produkts zweier Matrizen und ist hingegen unabhängig von der Reihenfolge:
Mit dem Determinantenproduktsatz gilt auch für die Determinante des Produkts zweier quadratischer Matrizen über einem kommutativen Ring:
Die Determinante des Produkts zweier nicht notwendigerweise quadratischer Matrizen kann mit dem Satz von Binet-Cauchy berechnet werden.
Algebraische Strukturen[Bearbeiten | Quelltext bearbeiten]
Ring der quadratischen Matrizen[Bearbeiten | Quelltext bearbeiten]
Die Menge der quadratischen Matrizen fester Größe bildet zusammen mit der Matrizenaddition und der Matrizenmultiplikation einen nichtkommutativen Ring, den Matrizenring . Das Nullelement dieses Rings ist die Nullmatrix . Ist ein unitärer Ring, dann ist auch der zugehörige Matrizenring unitär mit der Einheitsmatrix als Einselement, wobei für alle Matrizen
gilt. Die Nullmatrix fungiert im Matrizenring in diesem Fall als absorbierendes Element, das heißt, für alle Matrizen gilt dann:
Der Ring der quadratischen Matrizen ist jedoch nicht nullteilerfrei; aus folgt nicht notwendigerweise oder . Ein Beispiel wären zwei quadratische Matrizen mit je genau einem Eintrag ungleich Null an der gleichen Diagonalaußenstelle. Entsprechend darf bei Matrixgleichungen auch nicht gekürzt werden, denn aus folgt nicht notwendigerweise . Die Menge der quadratischen Matrizen über einem Körper bildet mit der Matrizenaddition, der Skalarmultiplikation und der Matrizenmultiplikation eine assoziative Algebra.
Gruppe der regulären Matrizen[Bearbeiten | Quelltext bearbeiten]
Die Menge der regulären Matrizen über einem unitären Ring bildet mit der Matrizenmultiplikation die allgemeine lineare Gruppe . Die zur Matrix inverse Matrix ist dann eindeutig über
definiert. Für die Inverse des Produkts zweier regulärer Matrizen gilt dann:
Durch die Invertierung wird die Reihenfolge bei der Multiplikation demnach ebenfalls vertauscht. Ist regulär, dann gilt auch die Kürzungsregel, das heißt aus oder folgt dann .
Gruppen der orthogonalen und unitären Matrizen[Bearbeiten | Quelltext bearbeiten]
Eine reelle quadratische Matrix heißt orthogonal, wenn
gilt. Die orthogonalen Matrizen bilden mit der Matrizenmultiplikation die orthogonale Gruppe , eine Untergruppe der allgemeinen linearen Gruppe . Entsprechend dazu heißt eine komplexe quadratische Matrix unitär, wenn
gilt. Die unitären Matrizen bilden mit der Matrizenmultiplikation die unitäre Gruppe , eine Untergruppe der allgemeinen linearen Gruppe .
Äquivalenzklassen von Matrizen[Bearbeiten | Quelltext bearbeiten]
Mit Hilfe der Matrizenmultiplikation werden Äquivalenzrelationen zwischen Matrizen über einem Körper definiert. Wichtige Äquivalenzrelationen sind:
- Äquivalenz: Zwei Matrizen und heißen äquivalent, wenn es zwei reguläre Matrizen und gibt, sodass gilt.
- Ähnlichkeit: Zwei quadratische Matrizen und heißen ähnlich, wenn es eine reguläre Matrix gibt, sodass gilt.
- Kongruenz: Zwei quadratische Matrizen und heißen kongruent, wenn es eine reguläre Matrix gibt, sodass gilt.
Matrizen, die durch solche Multiplikationen mit regulären Matrizen ineinander überführt werden können, bilden demnach Äquivalenzklassen.
Algorithmen[Bearbeiten | Quelltext bearbeiten]
Standardalgorithmus[Bearbeiten | Quelltext bearbeiten]
In Pseudocode kann die Matrizenmultiplikation wie folgt implementiert werden:
function matmult(A,B,l,m,n)
C = zeroes(l,n) // Ergebnismatrix C mit Nullen initialisieren
for i = 1 to l // Schleife über die Zeilen von C
for k = 1 to n // Schleife über die Spalten von C
for j = 1 to m // Schleife über die Spalten von A / Zeilen von B
C(i,k) = C(i,k) + A(i,j) * B(j,k) // Bildung der Produktsumme
end
end
end
return C
Die Reihenfolge der drei For-Schleifen kann dabei beliebig vertauscht werden, ohne das Ergebnis der Berechnung zu verändern. Da die drei Schleifen unabhängig voneinander sind, ist die Anzahl der benötigten Operationen von der Ordnung
- .
Die Zeitkomplexität des Algorithmus ist demnach für quadratische Matrizen kubisch, also von der Ordnung
- .
Bei der Matrix-Kettenmultiplikation, also der Multiplikation von drei oder mehr nichtquadratischen Matrizen, kann durch eine geschickte Wahl der Reihenfolge die Gesamtzahl arithmetischer Operationen minimiert werden.

Algorithmen mit besserer Komplexität[Bearbeiten | Quelltext bearbeiten]
Asymptotisch effizienter lassen sich zwei quadratische Matrizen mit dem Strassen-Algorithmus multiplizieren. Hierbei wird die Anzahl der Multiplikationen, die zur Multiplikation zweier -Matrizen benötigt werden, durch geschicktes Zusammenfassen von acht auf sieben reduziert, was auf Kosten zusätzlicher Additionen geschieht. Wendet man dieses Verfahren rekursiv an, ergibt sich eine Komplexitätsordnung von
- .
Allerdings lohnt sich der Strassen-Algorithmus aufgrund der in der Landau-Notation versteckten Konstanten nur für sehr große Matrizen.[3] Der Algorithmus mit der derzeit besten Komplexität ist eine Verbesserung des Coppersmith–Winograd-Algorithmus mit einer Laufzeit der näherungsweisen Ordnung[4]
- .
Für den praktischen Einsatz ist dieser Algorithmus jedoch nicht geeignet. Eine untere Schranke für die Komplexität der Matrizenmultiplikation ist
- ,
da jedes der Elemente der Ausgabematrix erzeugt werden muss. Die Ermittlung optimaler unterer und oberer Komplexitätsschranken für die Matrizenmultiplikation ist Gegenstand aktueller Forschung.
Ist eine der beiden Matrizen konstant, so kann lineare Berechnungscodierung verwendet werden.[5] Ihre asymptotische Komplexität ist
- ,
jedoch sind die versteckten Konstanten relativ klein, so dass bereits für Matrizen mit mehr als 20 bis 30 Zeilen oder Spalten eine Verbesserung gegenüber dem Standardverfahren erreicht werden kann.
Programmierung[Bearbeiten | Quelltext bearbeiten]
Das Matrizenprodukt ist in Programmiersystemen auf unterschiedliche Weise integriert, wobei insbesondere Verwechselungsgefahr mit dem komponentenweisen Hadamard-Produkt besteht. In den numerischen Softwarepaketen MATLAB und GNU Octave wird die Matrizenmultiplikation durch den Sternchen-Operator * realisiert, sodass A * B das Matrizenprodukt ergibt.[6] In anderen Programmierumgebungen, wie Fortran, Mathematica, R oder SciPy, wird jedoch durch A * B das Hadamard-Produkt berechnet. Die Matrixmultiplikation wird dann durch Funktionsaufrufe, wie matmul(A,B) in Fortran oder dot(A,B) in SciPy, oder durch eigene Operatoren für die Matrixmultiplikation, wie . in Mathematica oder %*% in R, umgesetzt.[7]

Verwendung[Bearbeiten | Quelltext bearbeiten]
Faktorisierungen[Bearbeiten | Quelltext bearbeiten]
In gewisser Weise ist die Umkehrung der Matrizenmultiplikation die Faktorisierung einer gegebenen Matrix als Produkt zweier Matrizen und , das heißt die Ermittlung einer Darstellung der Form
- .
Eine solche Faktorisierung ist nicht eindeutig, daher werden an die Matrizen und zusätzliche Anforderungen gestellt, wie Orthogonalität, Symmetrie oder eine bestimmte Besetzungsstruktur. Wichtige Zerlegungen reeller oder komplexer Matrizen dieser Art sind:
- die LR-Zerlegung einer quadratischen Matrix in eine untere und eine obere Dreiecksmatrix
- die Cholesky-Zerlegung, eine spezielle LR-Zerlegung einer symmetrisch positiv definiten Matrix
- die ILU-Zerlegung, eine Art unvollständige LR-Zerlegung speziell für dünnbesetzte Matrizen
- die QR-Zerlegung einer Matrix in eine orthogonale Matrix und eine obere Dreiecksmatrix
- die Schur-Zerlegung einer quadratischen Matrix in drei Matrizen: eine unitäre Matrix, eine obere Dreiecksmatrix und die Inverse der ersten Matrix
- die Singulärwertzerlegung einer Matrix in drei Matrizen: eine unitäre Matrix, eine Diagonalmatrix bestehend aus den Singulärwerten und die Adjungierte einer unitären Matrix
Solche Zerlegungen von Matrizen werden häufig in der numerischen linearen Algebra etwa zur Lösung linearer Gleichungssysteme oder Eigenwertprobleme eingesetzt. So lassen sich beispielsweise die Zeilen- und Spaltenumformungen im gaußschen Eliminationsverfahren als Produkt von Elementarmatrizen angeben.

Lineare Abbildungen[Bearbeiten | Quelltext bearbeiten]
Sind allgemein und zwei endlichdimensionale Vektorräume über dem gleichen Körper, dann kann jede lineare Abbildung nach Wahl je einer Basis in den beiden Vektorräumen über ihre Abbildungsmatrix dargestellt werden. Das Bild eines Vektors unter der Abbildung in den jeweiligen Basen kann dann über das Matrix-Vektor-Produkt
ermittelt werden. In der Geometrie lässt sich beispielsweise auf diese Weise jede Drehung um den Ursprung und jede Spiegelung an einer Ursprungsebene durch ein solches Matrix-Vektor-Produkt ausführen. Ist nun ein weiterer Vektorraum und eine weitere lineare Abbildung, dann gilt für die Abbildungsmatrix der Hintereinanderausführung dieser beiden Abbildungen:
Die Abbildungsmatrix einer Hintereinanderausführung zweier linearer Abbildungen ist also das Matrizenprodukt der beiden zugehörigen Abbildungsmatrizen. Auf diese Weise lässt sich beispielsweise jede Drehspiegelung als Produkt einer Drehmatrix und einer Spiegelungsmatrix darstellen. Alternativ kann eine lineare Abbildung auch durch Vektor-Matrix-Multiplikation eines Zeilenvektors mit der transponierten Abbildungsmatrix durchgeführt werden. Die Hintereinanderausführung von Abbildungen entspricht dann einer Matrizenmultiplikation von rechts statt von links.
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Anwendungen der Matrizenmultiplikation finden sich unter anderem:
- in der Analysis bei der Komposition differenzierbarer Funktionen mehrerer Variablen nach der mehrdimensionalen Kettenregel
- in der Computergrafik bei der Durchführung von Koordinatentransformationen in einer Grafikpipeline
- in der Optik bei der Berechnung von Lichtstrahlen durch optische Bauelemente mittels der Matrizenoptik
- in der Ökonomie bei der Input-Output-Analyse einer Produktion sowie bei der innerbetrieblichen Materialverflechtung[8]
- in der Robotik bei der Beschreibung kinematischer Ketten mittels der Denavit-Hartenberg-Transformation
- in der Elektrotechnik bei der Zweitortheorie elektrischer Netzwerke
- in der Quantenmechanik im Rahmen der Matrizenmechanik, hier auch für „unendlich große“ Matrizen
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Matrizen über Halbringen[Bearbeiten | Quelltext bearbeiten]
Allgemeiner können Matrizen über einem Halbring betrachtet werden, wobei die wichtigsten Eigenschaften der Matrizenmultiplikation, wie Assoziativität und Distributivität, erhalten bleiben. Entsprechend bildet dann den Halbring der quadratischen Matrizen über . Die Nullmatrix ist im Matrizenhalbring wieder das Nullelement und auch absorbierend, wenn das Nullelement im zugrunde liegenden Halbring absorbierend ist. Ist der zugrunde liegende Halbring unitär, dann bildet auch die Einheitsmatrix wieder das Einselement im Matrizenhalbring.
Wichtige Beispiele für Halbringe sind distributive Verbände, wie beispielsweise boolesche Algebren. Fasst man die Elemente eines solchen Verbands als Wahrheitswerte auf, so sind Matrizen über einem Verband zweistellige Relationen. Die Matrizenmultiplikation entspricht in diesem Fall der Komposition von Relationen.
Matrizenkategorien[Bearbeiten | Quelltext bearbeiten]
Algebraische Strukturen wie Ringe und Gruppen, deren Elemente Matrizen sind, sind auf quadratische Matrizen fester Größe beschränkt. Die Matrizenmultiplikation ist dagegen nicht derartig eingeschränkt. Eine Möglichkeit, diese Einschränkung aufzuheben, ist es, stattdessen Kategorien von Matrizen, jeweils über einem festen unitären Ring oder Halbring, zu betrachten. Die Objekte sind natürliche Zahlen, und ein Pfeil ist eine -Matrix. Die Komposition von Pfeilen ist durch die Matrizenmultiplikation gegeben. Sollen Matrizen auch addiert werden können, handelt es sich um eine präadditive Kategorie. Wenn Matrizen aller endlichen Größen vorkommen, erhält man eine abelsche Kategorie. Wenn nur invertierbare Matrizen vorkommen, handelt es sich um ein Gruppoid. In diesem Fall kann es interessant sein, anstelle der natürlichen Zahlen beliebige endliche Mengen als Objekte zuzulassen.
Verwandte Produkte[Bearbeiten | Quelltext bearbeiten]
Neben dem Matrizenprodukt existieren noch eine Reihe weiterer Produkte von Matrizen:
- Das Hadamard-Produkt zweier Matrizen ergibt eine Matrix, deren Einträge einfach durch komponentenweise Multiplikation der Einträge der Ausgangsmatrizen ermittelt werden. Im Vergleich zum Matrizenprodukt ist es jedoch weit weniger bedeutend.
- Das Kronecker-Produkt zweier Matrizen ergibt eine große Matrix, die durch Betrachtung aller möglichen Produkte von Einträgen der beiden Ausgangsmatrizen entsteht.
- Das Frobenius-Skalarprodukt zweier reeller oder komplexer Matrizen ergibt eine Zahl, die sich durch komponentenweise Multiplikation der Einträge der Ausgangsmatrizen und nachfolgende Summation all dieser Produkte berechnet. Im komplexen Fall wird dabei immer ein Eintrag komplex konjugiert.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Tilo Arens, Frank Hettlich, Christian Karpfinger, Ulrich Kockelkorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 2. Auflage. Spektrum Akademischer Verlag, 2011, ISBN 3-8274-2347-3.
- Michael Artin: Algebra. Springer, 1998, ISBN 3-7643-5938-2.
- Gene Golub, Charles van Loan: Matrix Computations. JHU Press, 2012, ISBN 1-4214-0794-9.
- Charles Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – eine Einführung. Oldenbourg, 2010, ISBN 3-486-59002-2.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Matrix Multiplication. In: MathWorld (englisch).
- djao: Matrix operations. In: PlanetMath. (englisch)
- Matrixmultiplikation Online Rechner
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ John J. O’Connor, Edmund F. Robertson: Jacques Philippe Marie Binet. In: MacTutor History of Mathematics archive (englisch).
- ↑ Horst Stöcker: Taschenbuch mathematischer Formeln und moderner Verfahren. Verlag Harri Deutsch, Frankfurt am Main 2007, ISBN 978-3-8171-1811-3, S. 371.
- ↑ Paolo D’Alberto, Alexandru Nicolau: Using recursion to boost ATLAS’s performance. In: High-Performance Computing (= Lecture Notes in Computer Science). Volume 4759. Springer, 2010, S. 142–151, doi:10.1007/978-3-540-77704-5_12.
- ↑ Virginia Vassilevska Williams: Multiplying matrices faster than coppersmith-winograd. In: STOC ’12 Proceedings of the 44th symposium on Theory of Computing. ACM, 2012, S. 887–898, doi:10.1145/2213977.2214056.
- ↑ Ralf R. Müller, Bernhard Gäde, Ali Bereyhi: Linear computation coding. 2021, arxiv:2102.00398 (PDF [abgerufen am 16. Dezember 2021]).
- ↑ Christoph W. Überhuber, Stefan Katzenbeisser, Dirk Praetorius: MATLAB 7: Eine Einführung. Springer, 2007, S. 81.
- ↑ NumPy for Matlab Users. SciPy.org, 22. Februar 2014, abgerufen am 3. Januar 2015.
- ↑ Christoph Mayer,David Francas,Carsten Weber: Lineare Algebra für Wirtschaftswissenschaftler. 3. Auflage. GBV Fachverlage, Wiesbaden 2007, ISBN 978-3-8349-9529-2, S. 75 f.































































































































