Erweiterte reelle Zahl
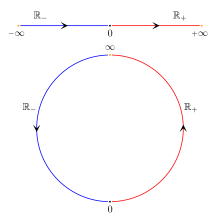
Als erweiterte reelle Zahlen bezeichnet man in der Mathematik eine Menge, die aus dem Körper der reellen Zahlen durch Hinzufügen neuer Symbole für unendliche Elemente (auch: uneigentliche Punkte) entsteht. Man unterscheidet genauer zwischen den affin erweiterten reellen Zahlen, bei denen es zwei vorzeichenbehaftete uneigentliche Punkte gibt, und den projektiv erweiterten reellen Zahlen mit nur einem vorzeichenlosen uneigentlichen Punkt. Ohne den Zusatz affin bzw. projektiv wird der Begriff erweiterte reelle Zahlen in der Literatur üblicherweise gleichbedeutend mit affin erweiterte reelle Zahlen verwendet, in diesem Artikel wird dieser jedoch als gemeinsamer Oberbegriff für beide Erweiterungen genutzt.
Beispielsweise machen die affin erweiterten reellen Zahlen es möglich, die unendlichen Elemente als den Grenzwert von bestimmt divergenten Folgen anzusehen und somit solche Folgen analog zu konvergenten Folgen zu behandeln. Die Definition der Erweiterungen ist dementsprechend zunächst topologisch motiviert. Die Arithmetik der reellen Zahlen lässt sich dagegen auf die erweiterten reellen Zahlen nicht vollständig fortsetzen.
Definition[Bearbeiten | Quelltext bearbeiten]
Die reellen Zahlen bilden mit ihrer üblichen Topologie einen lokalkompakten Raum. Durch geeignetes Hinzufügen uneigentlicher Punkte entsteht hieraus ein kompakter Raum.
- Bei der affinen Erweiterung ergänzt man um zwei Elemente und als vorzeichenbehaftete Unendlichkeiten zu . Mit werden zunächst einfach zwei beliebige Nicht-Elemente der reellen Zahlen bezeichnet.
- Im Fall der projektiven Erweiterung betrachtet man die Einpunktkompaktifizierung (auch die Bezeichnung ist zu finden) mit einem einzigen durch das Symbol bezeichneten uneigentlichen Punkt.
Topologie[Bearbeiten | Quelltext bearbeiten]
Jede in offene Menge sei auch in bzw. offen. Zusätzlich wird eine Umgebungsbasis für die uneigentlichen Punkte angegeben.
Affiner Fall[Bearbeiten | Quelltext bearbeiten]
Für jedes soll
eine offene Umgebung von und
eine offene Umgebung von sein. Hierdurch wird beispielsweise die durch gegebene Folge zu einer gegen konvergenten Folge: Für jedes sind fast alle Folgenglieder in enthalten, nämlich all jene mit .
Die Abbildung , die durch
- für , ,
gegeben ist, ist ein Homöomorphismus. Topologisch ist also gleichwertig mit einem abgeschlossenen Intervall, das mit bezeichnet wird.
Die affin erweiterten reellen Zahlen bilden eine streng total geordnete Menge, indem die Ordnung der reellen Zahlen durch , für alle sowie fortgesetzt wird. Die üblichen Schreibweisen für offene, und für halb-offene und für geschlossene Intervalle sind somit auch sinnvoll, wenn und/oder ist. Die Topologie von ist zugleich die von dieser Ordnung definierte Ordnungstopologie.
Die Homöomorphie mit zeigt, dass metrisierbar ist. Allerdings lässt sich die Standardmetrik auf nicht zu einer Metrik auf fortsetzen: dazu müsste offen sein, also eine „Kreisfläche“ mit Mittelpunkt und Radius <1 enthalten, woraus aber
folgen würde.
Projektiver Fall[Bearbeiten | Quelltext bearbeiten]
Für jede positive reelle Zahl soll das Komplement von offene Umgebung von sein. Allgemeiner folgt so, wie für die Einpunktkompaktifizierung üblich, dass für jede kompakte Teilmenge das Komplement eine offene Umgebung von ist. Hierdurch wird beispielsweise auch die durch gegebene Folge zu einer gegen konvergenten Folge: Für jedes sind fast alle Folgenglieder im Komplement von enthalten, d. h. es gilt . Allgemein wird aus jeder dem Betrage nach bestimmt divergenten reellen Folge eine in gegen konvergente.
Mit dieser Topologie wird homöomorph zur Kreislinie
Ein Homöomorphismus ist beispielsweise gegeben durch
- für und .
Ebenso wenig wie die Kreislinie lässt sich daher in mit der Topologie verträglicher Weise total ordnen. Üblicherweise belässt man es dabei, dass mit endlichen Zahlen unvergleichbar ist.
Wie im affinen Fall ist auch die projektive Erweiterung metrisierbar, jedoch nicht durch Fortsetzen der reellen Standardmetrik.
Man kann sich auch als aus durch Zusammenkleben der Punkte und entstanden denken.
Zudem entspricht der reellen projektiven Geraden , dies motiviert auch die Bezeichnung.
Gemeinsame Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Sowohl die affine als auch die projektive Erweiterung bilden einen kompakten Raum, in dem die reellen Zahlen eine dichte Teilmenge sind. Hieraus ergibt sich, dass jede Zahlenfolge dann eine konvergente Teilfolge (und sei es gegen einen uneigentlichen Punkt) enthält. Nur bestimmt bzw. betragsmäßig bestimmt divergente reelle Folgen werden in der affin bzw. projektiven Erweiterung zu konvergenten Folgen. Eine Folge wie die durch gegebene ist auch in den erweiterten reellen Zahlen divergent. In der Stone-Čech-Kompaktifizierung der reellen Zahlen dagegen konvergieren alle beschränkten Folgen.
Vereinfachte Schreibweisen[Bearbeiten | Quelltext bearbeiten]
Die Einführung der (affin) erweiterten reellen Zahlen erlaubt es zunächst, die Schreibweisen und analog zu mit endlichem zu behandeln, ohne dies als eigene Notation oder Sprechweise gesondert einzuführen. Auch ohnedies lediglich symbolische Schreibweisen wie für bestimmt divergente Folgen gliedern sich nahtlos in den Fall konvergenter Folgen ein.
Arithmetik[Bearbeiten | Quelltext bearbeiten]
Es stellt sich die Frage, wie die mathematischen Grundrechenarten an die neuen unendlichen Stellen angepasst werden sollen. Im Sinne des Permanenzprinzips sollen hierbei alte Rechenregeln fortbestehen, aber durchgängig ist dies nicht machbar, da die erweiterten reellen Zahlen keinen vollständig geordneten Körper bilden können – ein solcher müsste wieder isomorph (und homöomorph) zu sein. Mindestens für einige Argumente bleiben die Operationen also undefiniert.
Für bzw. möchte man für möglichst viele einen wiederum in liegenden Wert für die Ausdrücke
derart definieren, dass die üblichen Rechengesetze (insb. Assoziativgesetz und Kommutativgesetz von Addition und Multiplikation sowie das Distributivgesetz) auch für diese Erweiterung gültig bleiben. Genauer lautet eine sinnvolle Forderung: Stimmen zwei Ausdrücke in endlich vielen Variablen im Endlichen stets überein, sofern beide Seiten (also auch alle benutzten Teilausdrücke) definiert sind, und ist auch nicht aus trivialen Gründen stets eine Seite undefiniert, so soll diese Gleichheit der beiden Ausdrücke auch in der Erweiterung gelten, also wenn auch unendliche Werte für die Variablen zugelassen sind und alle Teilausdrücke definiert sind. Eine solche Gleichung ist beispielsweise . Im Endlichen gilt dies für , d. h. sobald und definiert sind (das Produkt ist hier immer definiert). Wenn für den Fall in der Erweiterung definiert wird, muss entweder gelten oder das Produkt undefiniert sein.
Zusätzlich zu den Grundrechenarten interessiert noch die Potenzrechnung, d. h. man möchte dem Ausdruck für möglichst viele einen Wert so zuweisen, dass die Potenzgesetze , , immer dann gelten, wenn alle auftretenden Teilausdrücke definiert sind.
Rechenregeln aus Stetigkeit[Bearbeiten | Quelltext bearbeiten]
Die genannten (algebraisch formulierten) Bedingungen sind auf jeden Fall dann erfüllt, wenn die Operationen stetig fortgesetzt werden. Es gibt jedoch beispielsweise keine stetige Abbildung bzw. , die auf mit der Addition übereinstimmt. Daher ist die stetige Fortsetzung grundsätzlich nur partiell möglich. Durch möglichst weitreichende stetige Fortsetzung ergeben sich folgende Rechenregeln, bei denen für auf diesem Wege nicht zu definierende Ausdrücke der Wert „?“ notiert wird:
Grundrechenarten[Bearbeiten | Quelltext bearbeiten]
| in | in |
|---|---|
| Vergleiche | |
|
|
| Negation | |
|
|
|
| Addition und Subtraktion | |
|
|
|
|
|
| Multiplikation | |
|
|
|
|
|
| Kehrwerte | |
|
|
|
|
|
|
| Division | |
|
|
|
|
Potenzen[Bearbeiten | Quelltext bearbeiten]

Im Folgenden wird nur im affinen Fall die stetige Fortsetzung des Potenzierens angegeben. Hierbei ist zu beachten, dass bereits im Endlichen nur (reell) definiert ist, wenn (und beliebig) oder und oder und .
| Ausdruck | Wert | Bedingung |
|---|---|---|
| ? | oder | |
| oder | ||
| ? | ||
| und ist keine ungerade ganze Zahl | ||
| ? | ist eine negative ungerade ganze Zahl | |
| ? | ||
| ? | ||
| ganzzahlig | ||
| und ganzzahlig |
Der Wert von mit negativem und endlichem nicht-ganzen bleibt undefiniert, da diese Stellen nicht zum Abschluss des Definitionsbereiches der endlichen Potenzfunktion gehören. Zu den stetigen Fortsetzungen mit nichtpositiver Basis ist zu beachten, dass diese Stellen zwar zum Abschluss des Definitionsbereiches gehören, aber keine inneren Punkte des Abschlusses sind. Es gibt daher gänzlich außerhalb des Definitionsbereiches liegende Folgen, die gegen diese Stellen konvergieren.
Funktionswerte[Bearbeiten | Quelltext bearbeiten]
Einige Standardfunktionen lassen sich stetig ins Unendliche zu Abbildungen fortsetzen, so etwa
- und (in ist jedoch nicht definiert).
In der Maßtheorie wird eine Funktion mit einer nichtleeren Menge numerisch genannt. Numerische Funktionen können als Supremum oder Infimum einer Folge reeller Funktionen auftreten. Auch in der Optimierung werden teilweise aus praktischen Gründen die Funktionswerte zugelassen. Funktionen, die diese Werte annehmen heißen erweiterte Funktionen.
Undefinierte Ausdrücke[Bearbeiten | Quelltext bearbeiten]
Mit der Methode der stetigen Fortsetzung lässt sich in für die Grundrechnungsarten-Ausdrücke
bzw. in für
kein Wert angeben. Prinzipiell wäre es denkbar, eine geeignete – notwendig unstetige – Festsetzung zu finden. Das ist für die genannten Ausdrücke jedoch nicht möglich, ohne das Permanenzprinzip zu verletzen, d. h. ohne Widerspruch zu den üblichen Rechenregeln. Dies zeigt im Einzelnen die folgende Aufstellung:
- :
- Wegen für alle folgt durch das Permanenzprinzip, dass gelten sollte, wenn der Ausdruck definiert ist. Dies führt jedoch unter Berücksichtigung der Rechenregel auf den Widerspruch .
- in :
- Analog, da .
- :
- Wegen für alle soll gelten. Andererseits gilt , soweit die linke Seite definiert ist. Demnach ergibt sich der Widerspruch
- :
- Wegen und ergibt sich
- :
- Auch hier folgt .
- in :
- Aus folgt, dass gelten soll, folglich . Wegen folgt .
Den aufgelisteten Ausdrücken einen Wert zuzuweisen, ist also auf „vernünftige“ Weise nicht möglich. Abgesehen von mit werden die so in nicht definierten Ausdrücke auch als unbestimmte Ausdrücke bezeichnet, für die es allerdings in bestimmten Einzelfällen gleichwohl möglich ist, mittels der Regel von de L’Hospital gültige Zahlenwerte zu berechnen.
Abweichend von obiger Liste wird in einigen Gebieten der Mathematik, namentlich der Maßtheorie, gewöhnlich vereinbart, da auf diese Weise zahlreiche Aussagen konziser[1] zu fassen sind. In dem Fall ist darauf zu achten, dass niemals der Kehrwert von unendlich benutzt wird, bzw. es ist auf die Festsetzung zu verzichten. Andernfalls müssten die Ausnahmen der gewöhnlichen Rechenregeln (nämlich, dass nicht immer gilt) regelmäßig durch Fallunterscheidungen bedacht werden, und dies machte den Vorteil der Abkürzung wieder wett.
Algebraische Fortsetzung des Potenzierens[Bearbeiten | Quelltext bearbeiten]
Anders als bei den vier Grundrechenarten ist es auch unabhängig von Stetigkeitsbetrachtungen möglich, konsistent (aber unstetig)
zu definieren.[2] Dass zumindest kein anderer Wert für diese Ausdrücke definiert werden kann, ergibt sich direkt aus dem Permanenzprinzip, da im Endlichen gilt. Diese Festsetzungen sind konsistent in dem Sinne, dass die Potenzgesetze , und gelten, wann immer alle Teilausdrücke definiert sind.
Im Zusammenhang mit Grenzwertuntersuchungen jedoch werden die Ausdrücke , und sogar mit zu den unbestimmten Ausdrücken gezählt, da in dem Zusammenhang Stetigkeit ausschlaggebend ist. In bestimmten Einzelfällen allerdings ist es auch hier möglich, mittels der Regel von de L’Hospital für die o. g. Ausdrücke gültige Zahlenwerte zu berechnen.
Das Lösen von Gleichungen[Bearbeiten | Quelltext bearbeiten]
Beim Lösen von Gleichungen ist Vorsicht geboten, wenn man mit Unendlichkeiten arbeitet, da zusätzliche Lösungen existieren können. Besonders offensichtlich wird dies bei der Gleichung , die für endliche stets genau eine Lösung hat. Dagegen hat gar keine und unendlich viele. Einige weitere Beispiele, die sich aus den obigen Rechenregeln ergeben, zeigt die folgende Tabelle:
| Gleichung | Lösungen in | Zusätzlich in | Zusätzlich in |
|---|---|---|---|
Beim Umformen von Gleichungen kann nicht mehr allgemein auf die Kürzungseigenschaft der Addition (aus folgt ) zurückgegriffen werden, sondern nur unter der Voraussetzung, dass endlich ist. Die Kürzungseigenschaft der Multiplikation (aus folgt ), die auch im Endlichen nur unter der Voraussetzung gilt, ist ebenfalls für unendliches ungültig. Die letzte Gleichung aus obiger Tabelle, , lässt sich nicht äquivalent umformen zu , denn diese hat im Gegensatz zu ersterer keine unendliche Lösung (für ist die rechte Seite nicht definiert).
Komplexe Zahlen[Bearbeiten | Quelltext bearbeiten]
Wenn man statt von den reellen von den komplexen Zahlen ausgeht, betrachtet man hauptsächlich die zu einer Sphäre homöomorphe Einpunktkompaktifizierung (Riemannsche Zahlenkugel). Die Rechenregeln für die Grundrechenarten stimmen hierbei im Wesentlichen mit denen für die Einpunktkompaktifizierung von überein. Es gibt auch hier alternative Ansätze, bei denen zu einer abgeschlossenen Kreisscheibe oder zur projektiven Ebene kompaktifiziert wird.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ konzis (Eintrag „konzis“ im Wiktionary)
- ↑ Wolfram Alpha liefert zwar Indeterminate als Ergebnis von (Eingabe: 1^Infinity), andererseits 1 für (Eingabe: prod_{n=1}^Infinity 1).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Davic W. Cantrell: Affinely Extended Real Numbers. In: MathWorld. Wolfram Research Inc., abgerufen am 27. Juli 2010 (englisch).
- Davic W. Cantrell: Projectively Extended Real Numbers. In: MathWorld. Wolfram Research Inc., abgerufen am 27. Juli 2010 (englisch).












![{\displaystyle \left]a,+\infty \right]:=\{x\in \mathbb {R} \mid x>a\}\cup \{+\infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25ad808955c3c6c8ce4b4f3ff27c1f23902b3b2a)


![{\displaystyle ]a,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c91921578261a19380a689f7a8ee3f33904f7fe)

![{\displaystyle f\colon {\overline {\mathbb {R} }}\to [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3533afcc105f3b08ad7cd9b2b411a3e056b17f5)




![{\displaystyle [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7a5a5ba47896e8fdd43cf7f311db27350f0f8ff)



![{\displaystyle ]a,b[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b51ec208e9582e11a4f340a42d4f17fb4748fcb)

![{\displaystyle ]a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/784ada3a213049f80d0909d4b95b4b8a7f871e83)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)




![{\displaystyle [-r,r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dbcf3f99b353b618465500fe9576e0850885ffd)


































































































































































