Fensterfunktion
Eine Fensterfunktion legt in der digitalen Signalverarbeitung fest, mit welcher Gewichtung die bei der Abtastung eines Signals gewonnenen Abtastwerte innerhalb eines Ausschnittes (Fenster) in nachfolgende Berechnungen eingehen.
Fensterfunktionen werden u. a. bei der Frequenzanalyse (z. B. mittels diskreter Fouriertransformation), beim Filterdesign und beim Beamforming eingesetzt.
Anwendungen[Bearbeiten | Quelltext bearbeiten]
Frequenzanalyse[Bearbeiten | Quelltext bearbeiten]
Ein andauerndes Signal wird in der Regel in Blöcken verarbeitet. Da Blocklängen in der Praxis endlich sind, kommt es zum sogenannten Leck-Effekt (englisch leakage effect), wenn die Blocklänge nicht gerade ein natürlichzahliges Vielfaches der Periode des Signals ist. Das errechnete Frequenzspektrum wird zu breit, es ist bildlich gesprochen „verschmiert“. Dieser Effekt resultiert aus den Eigenschaften der Fourier-Transformation.
Durch die Verwendung einer geeigneten Fensterfunktion lässt sich der Effekt vermindern, aber nicht ganz vermeiden. Das Signal wird hierbei meistens am Fensterbeginn „eingeblendet“ und am Fensterende „ausgeblendet“, was zu einer künstlichen Periodisierung des Signals innerhalb der Zeitfensterlänge führt.
Die Fensterfunktion beeinflusst neben der spektralen Verbreiterung außerdem die Frequenzselektivität und den maximal möglichen spektralen Fehler. Es gibt verschiedene Fensterfunktionen unterschiedlicher Komplexität. Die Auswahl einer passenden Fensterfunktion ist daher stets ein Kompromiss, der den speziellen Anforderungen des jeweiligen Anwendungsfalls Rechnung trägt.
Filterdesign[Bearbeiten | Quelltext bearbeiten]
Eine häufig angewandte Methode für das Design von digitalen Filtern mit endlicher Impulsantwort (FIR-Filter) ist die Fenstermethode (engl. window method).
Dabei wird der gewünschte Frequenzgang des Filters definiert und mit der inversen Fouriertransformation die ideale Impulsantwort ermittelt. Das Resultat der inversen Fouriertransformation ist in der Regel unendlich lang. Um eine endlich lange Impulsantwort mit der gewünschten Filterlänge N zu erhalten, wird durch eine Fensterfunktion ein Ausschnitt der unendlichen Impulsantwort ausgewählt. Der tatsächliche Frequenzgang des Filters entspricht somit der Multiplikation des gewünschten Frequenzgangs mit der Fouriertransformierten der Fensterfunktion.
Im Filterdesign führen breite (selektive) Fensterfunktionen zu steilen Übergängen zwischen Durchlass- und Sperrbereich, aber zu geringer Sperrdämpfung. Schmale (nicht selektive) Fensterfunktionen führen zu flachen Übergängen zwischen Durchlass- und Sperrbereich, dafür aber zu großer Sperrdämpfung.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Im Folgenden sind gebräuchliche Fensterfunktionen dargestellt. In den Grafiken sind in der linken Darstellung die diskreten Fensterfunktion mit -Werten dargestellt, außerhalb des dargestellten Bereiches weist jede Fensterfunktion den in den Grafiken nicht explizit dargestellten Wert 0 auf. In der rechten Darstellung ist das der Fensterfunktion zugeordnete Frequenzspektrum mit 128 Frequenzkomponenten abgebildet und wie es durch die Diskrete Fourier-Transformation (DFT) gewonnen wird. Das Signal wird im Frequenzbereich mit diesem Spektrum der Fensterfunktion gefaltet, wobei die Bewertung von idealen Fensterfunktionen meist durch ein schmales Spektrum um die Mittenfrequenz und starke Dämpfungen außerhalb gekennzeichnet ist.
Dabei ist eine ganzzahlige Fensterbreite. Der aktuelle Index des Eingangssignals ist . Wenn nicht anders vermerkt, geht in folgenden Darstellungen , das Maximum befindet sich bei . Daneben existiert auch eine gleichwertige und in der Phase verschobene und symmetrische Darstellung um 0, auch als englisch zero phase bezeichnet. In diesem Fall geht der Index von
das Maximum befindet sich bei dieser Darstellungsform bei .
Rechteck-Fenster[Bearbeiten | Quelltext bearbeiten]

Die Rechteck-Fensterfunktion, auch bezeichnet als Dirichlet-Fenster (nach Peter Gustav Lejeune Dirichlet), ist im gesamten Fensterbereich 1 und außerhalb 0. Die Funktion ist gegeben als:
Die einfache Verarbeitung des Eingangssignals in Blöcken entspricht der Anwendung dieser Fensterfunktion. Das Betragsspektrum entspricht dem Betragsverlauf der si-Funktion. Nur im Sonderfall, wenn die Fensterbreite exakt ein ganzzahliges Vielfaches der Periodendauer der harmonischen Signalschwingung umfasst, tritt bei zeitdiskreten Signalen zufolge der Fensterung mit dem Rechteck-Fenster kein Leck-Effekt auf.
Von-Hann-Fenster [Bearbeiten | Quelltext bearbeiten]

Das Von-Hann-Fenster basiert auf einer Überlagerung von drei spektral gegeneinander verschobenen si-Funktionen um gegenüber dem Rechteck-Fenster mit nur einer si-Funktion im Spektrum eine stärkere Unterdrückung der Nebenkeulen zu erreichen. Der Nachteil ist eine Reduktion in der Frequenzauflösung.[1] Das Von-Hann-Fenster mit der Haversine-Funktion wird auch als Raised-Cosinus-Fenster bezeichnet, mit folgender Funktion:
mit
Dies ist auch in nebenstehender Abbildung dargestellt.
Daneben wird in der Literatur auch die symmetrische Darstellung mit der Havercosine-Funktion um und ohne Phasenversatz verwendet:
und in diesem Fall mit dem Index im Bereich
Die Bezeichnung Hann-Fenster stammt aus der Publikation „Particular Pairs of Windows“[2] von R. B. Blackman und John W. Tukey, die dieses nach Julius von Hann benannt haben. Aus diesem Artikel stammt auch die weit verbreitete Bezeichnung Hanning-Fenster, wobei dort jedoch lediglich die Anwendung des Hann-Fensters als „hanning“ (abgeleitet von „to hann“) bezeichnet wird.
Hamming-Fenster[Bearbeiten | Quelltext bearbeiten]

Die Funktion ist gegeben als
dabei ist die Fensterbreite und der aktuelle Index des Eingangssignals.
Diese Fensterfunktion ist benannt nach Richard Hamming und stellt eine Abwandlung des Von-Hann-Fensters dar. Allgemein lassen sich das Von-Hann- und das Hamming-Fenster mit den beiden Koeffizienten und ausdrücken als:
Die beiden Koeffizienten sind bei dem Von-Hann-Fenster 0,5. Das Maximum der Fensterfunktion ist gleich . Normiert man das Fenster so, dass , dann bleibt noch ein Freiheitsgrad übrig. Bei dem Hamming-Fenster werden die Koeffizienten so gewählt, dass die Nullstellen der beiden benachbarten und größten Nebenkeulen maximal unterdrückt werden. Dies entspricht einer unterschiedlichen Gewichtung der einzelnen si-Funktionen im Spektrum der Fensterfunktion.[3] Aus dieser Bedingung ergibt sich für
Durch die Rundung auf zwei Nachkommastellen für praktische Implementierungen ergibt sich bei dem Hamming-Fenster eine Dämpfung der beiden ersten Nebenkeulen von ca. −42,76 dB.[3]
Blackman-Fenster (3-Term)[Bearbeiten | Quelltext bearbeiten]
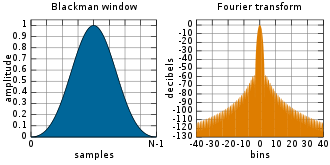
Blackman-Fenster sind definiert als:
mit
und
Üblicherweise wird beim klassischen Blackman-Fenster gewählt.
Blackman-Harris-Fenster[Bearbeiten | Quelltext bearbeiten]
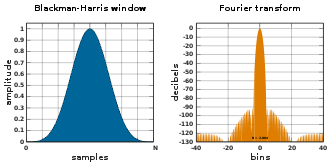
Funktion:
mit
Frederic J. Harris veröffentlichte diese Funktion 1978 als Abwandlung der Blackman-Fensterfunktion.[4]
Blackman-Nuttall-Fenster[Bearbeiten | Quelltext bearbeiten]

Funktion:
mit
Das Blackman-Nuttall-Fenster ist bis auf die vier fast identischen Koeffizienten identisch mit dem Blackman-Harris-Fenster, was den Einfluss der notwendigen Genauigkeit bei der Implementierung der Koeffizienten bei dieser Klasse von Fensterfunktionen verdeutlicht.
Flat-Top-Fenster[Bearbeiten | Quelltext bearbeiten]

Das Flat-Top-Fenster ist eine teilweise negativ bewertende Fensterfunktion, welche unter anderem in Spektrumanalysatoren für die Messung und Bewertung des Betrags von einzelnen Amplituden eingesetzt wird. Das Flat-Top-Fenster weist einen vergleichsweise kleinen Amplitudenfehler auf, nachteilig ist die schlechte Frequenzauflösung.[5]
Als ein Beispiel wird im Spektrumanalysator SR785 von Stanford Research Systems (SRS) folgende Flat-Top-Fensterfunktion eingesetzt, wie auch in nebenstehender Abbildung dargestellt:[6]
mit
Bartlett-Fenster[Bearbeiten | Quelltext bearbeiten]

Diese Fensterfunktion ist nach Albert Charles Bartlett benannt:

Eine eng verwandte Variation der Bartlett-Fensterfunktion basiert auf der Dreiecksfunktion und weist als Unterschied an den Anfangs- bzw. Endwerten keine Nullwerte auf. Sie ist definiert als
Das Dreieckfunktion-Fenster kann als eine Faltung zweier Rechteckfenster aufgefasst werden, die Hauptkeule ist doppelt so breit wie bei dem Rechteckfenster und die nächste Nebenkeule weist eine Dämpfung um −26 dB auf.[7]
Bartlett-Hann-Fenster[Bearbeiten | Quelltext bearbeiten]
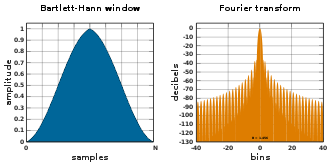
Dies ist eine Kombination der Dreiecksfunktion des Bartlett-Funktion mit der Hann-Fensterfunktion:
mit
Kosinus-Fenster[Bearbeiten | Quelltext bearbeiten]

Die Kosinus-Fensterfunktion ist auch als Sinus-Fensterfunktion bekannt. Sie ist definiert als:
Tukey-Fenster[Bearbeiten | Quelltext bearbeiten]

Die Tukey-Fensterfunktion, benannt nach John W. Tukey, kann als eine auf Abtastwerte abgeflachte Kosinus-Fensterfunktion, welche mit einem Rechteckfenster der Breite gefaltet wird, aufgefasst werden. Für geht die Tukey-Fensterfunktion in das Rechteckfenster über. Für entspricht sie dem Hann-Fenster.[8][4]
Lanczos-Fenster[Bearbeiten | Quelltext bearbeiten]

Das Lanczos-Fenster basiert auf der normierten si-Funktion, ähnlich wie der Lanczos-Filter:
Kaiser-Fenster[Bearbeiten | Quelltext bearbeiten]


Das Fenster ist definiert durch die Funktion:[9]
Dabei ist die modifizierte Besselfunktion nullter Ordnung. Die Fensterbreite beträgt und ist ein reeller Faktor, welcher die Form des Fensters bestimmt. Je größer , desto schmaler wird das Fenster und entspricht einem Rechteckfenster.
Die Fouriertransformierte des Fensters ist definiert durch die Funktion
für die normierte Frequenz .
Mit der Funktion lässt sich die Breite des Hauptmaximums
und die relative Dämpfung des Nebenmaximums
berechnen. Daraus ergibt sich: Wenn größer wird, nimmt die Breite des Hauptmaximums zu und die relative Amplitude des Nebenmaximums ab.
Gauß-Fenster[Bearbeiten | Quelltext bearbeiten]

Das Gauß-Fenster basiert auf der Gaußschen Glockenkurve, welche sich bis nach unendlich ausdehnt und daher zeitlich begrenzt ausgeführt werden muss. Dies bedeutet eine Kombination mit dem Rechteck-Fenster.
Das Fenster ist gegeben als:
mit
Ultraspherical-Fenster[Bearbeiten | Quelltext bearbeiten]

Das Ultraspherical-Fenster wurde 1984 von Roy Streit[10] eingeführt und wird im Antennenarray-Design,[11] nicht-rekursiven Filterdesign,[10] und in der Spektrumanalyse verwendet.[12]
Wie andere einstellbare Fenster verfügt das Ultraspherical-Fenster über Parameter, mit denen die Fourier-Transformations-Hauptkeulenbreite und die relative Nebenkeulenamplitude gesteuert werden können. Ungewöhnlich für andere Fenster ist ein zusätzlicher Parameter, mit dem die Rate eingestellt werden kann, mit der die Amplitude der Nebenkeulen abnimmt (oder zunimmt).[12][13][14]
Das Fenster kann im Zeitbereich wie folgt ausgedrückt werden:[12]
Dabei ist das Gegenbauer-Polynom vom Grad N und die Kontrolle und die Nebenkeulenmuster.[12]
Bestimmte spezifische Werte von ergeben andere bekannte Fenster: und geben die Dolph-Chebyshev und Saramäki an Fenster jeweils.[10][15]
Weitere[Bearbeiten | Quelltext bearbeiten]
Vergleich[Bearbeiten | Quelltext bearbeiten]

Bewertungskriterien für Fensterfunktionen[Bearbeiten | Quelltext bearbeiten]
Alle gängigen Bewertungskriterien beziehen sich auf die Übertragungsfunktion (Fouriertransformation der Fensterfunktion) im Frequenzbereich. Zum Vergleich und zur Auswahl der richtigen Fensterfunktion werden die folgenden Bewertungskriterien verwendet:
Breite des Hauptmaximums (Hauptzipfels)[Bearbeiten | Quelltext bearbeiten]
Eine Verbreiterung des Hauptmaximums führt zu einem schnelleren Abfall der Nebenmaxima (Nebenzipfel), erhöht die Dynamik der Fensterfunktion und verringert den Leck-Effekt. Allerdings wird dabei die Frequenzselektivität verringert. Fensterfunktionen mit breitem Hauptmaximum werden deshalb auch als nichtselektive, dynamische Fenster bezeichnet, und solche mit schmalem Hauptmaximum als selektive, nichtdynamische Fenster.
Die Breite des Hauptmaximums wird meistens als 3-dB-Grenzfrequenz angegeben. Dies ist die Frequenz, bei der die Amplitude des Hauptmaximums um 3 dB abgefallen ist. Selten wird auch die gesamte Breite des Maximums bis zu den Nullstellen angegeben.
Relative Amplitude des Nebenmaximums[Bearbeiten | Quelltext bearbeiten]
Starke Nebenmaxima einer Fensterfunktion erhöhen den Leck-Effekt bei der Frequenzanalyse und deuten auf eine geringe Dynamik der Fensterfunktion hin.
Als Bewertungskriterium wird das Verhältnis zwischen der Amplitude des Hauptmaximums und der Amplitude des höchsten Nebenmaximums verwendet.
Leck-Faktor[Bearbeiten | Quelltext bearbeiten]
Der Leck-Effekt wird durch tiefe Nebenmaxima verringert. Der Leck-Faktor (engl. leakage factor) ist definiert als das Verhältnis der Leistung unter allen Nebenmaxima zur Leistung der gesamten Funktion.
Maximaler Abtastfehler[Bearbeiten | Quelltext bearbeiten]
Der maximale Abtastfehler ist definiert als das Verhältnis der Amplitude des Hauptmaximums zur Amplitude bei der Frequenz /Fensterlänge.

Vergleich nach oben genannten Bewertungskriterien[Bearbeiten | Quelltext bearbeiten]

Verbreiterung des Hauptmaximums führt zu schnellerem Abfall der Nebenmaxima. Exemplarisch ist dies in nebenstehender Abbildung an Rechteck- und Hamming-Fenster gezeigt.
| Fensterbezeichnung | rel. Amplitude des Nebenmaximums |
Breite des Hauptmaximums |
max. Abtastfehler |
|---|---|---|---|
| Rechteck | −13 dB | 3,92 dB | |
| Dreieck (Bartlett) | −25 dB | 1,82 dB | |
| von Hann | −31 dB | 1,42 dB | |
| Hamming | −41 dB | 1,78 dB | |
| Kaiser-Bessel () | −46 dB | 1,46 dB | |
| Kaiser-Bessel () | −82 dB | 0,89 dB | |
| Blackman | −57 dB | 1,10 dB |
Literatur[Bearbeiten | Quelltext bearbeiten]
- Karl-Dirk Kammeyer, Kristian Kroschel: Digitale Signalverarbeitung. 9. Auflage. Teubner, 2018, ISBN 3-8348-1644-2.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Julius O. Smith III: Generalized Hamming Window Family. Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, abgerufen am 31. August 2014.
- ↑ R. B. Blackman, J. W. Tukey: Particular pairs of windows. In: The measurement of power spectra, from the point of view of communications engineering. Dover, New York 1959, S. 95–101, hier S. 98–99.
- ↑ a b Julius O. Smith III: Hamming Window. Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, abgerufen am 30. August 2014.
- ↑ a b c F. J. Harris: On the use of windows for harmonic analysis with the discrete Fourier transform. In: Proceedings of the IEEE. Vol. 66, 1978, S. 51–83, doi:10.1109/PROC.1978.10837.
- ↑ Steven W. Smith: The Scientist and Engineer's Guide to Digital Signal Processing. Hrsg.: California Technical Publishing. San Diego, California, USA 2011 (dspguide.com [abgerufen am 14. Februar 2013]).
- ↑ G. Heinzel, A. Rüdiger, R. Schilling: Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows. Max Planck Institute (MPI) für Gravitationsphysik / Laser Interferometry & Gravitational Wave Astronomy, 2002, 395068.0 (mpg.de [abgerufen am 10. Februar 2013]).
- ↑ Julius O. Smith III: Properties. (Memento vom 6. Juli 2008 im Internet Archive) In: Spectral Audio Signal Processing. März 2007 (Draft/Entwurf).
- ↑ J.W. Tukey: An introduction to the calculations of numerical spectrum analysis. In: Spectral Analysis of Time Series. 1967, S. 25–46.
- ↑ J. Kaiser, R. W. Schafer: On the use of the I0-sinh window for spectrum analysis. In: IEEE Transactions on Acoustics, Speech and Signal Processing. Band 28, Nr. 1, Februar 1980, S. 105–107, doi:10.1109/TASSP.1980.1163349.
- ↑ a b c Peter Kabal: Time Windows for Linear Prediction of Speech. Version 2a Auflage. Dept. Elec. & Comp. Eng., McGill University, November 2009 (mcgill.ca [PDF; abgerufen am 23. Februar 2021] Technical Report).
- ↑ Roy L. Streit: A two-parameter family of weights for nonrecursive digital filters and antennas. In: IEEE Transactions on Acoustics, Speech, and Signal Processing. Band 32, Nr. 1, Februar 1984, S. 108–118, doi:10.1109/TASSP.1984.1164275.
- ↑ a b c d A. G. Deczky: Unispherical windows. In: ISCAS 2001. The 2001 IEEE International Symposium on Circuits and Systems (Cat. No. 01CH37196). Band 2, 2001, S. 85–88, doi:10.1109/ISCAS.2001.921012.
- ↑ Stuart W. A. Bergen, Andreas Antoniou: Design of Ultraspherical Window Functions with Prescribed Spectral Characteristics. In: EURASIP Journal on Advances in Signal Processing. Band 2004, Nr. 13, Dezember 2004, S. 1–13, doi:10.1155/S1110865704403114.
- ↑ Stuart W. A. Bergen: Design of the Ultraspherical Window Function and Its Applications. Dissertation 2005, University of Viktoria. 2005 (uvic.ca [PDF; abgerufen am 24. Februar 2021]).
- ↑ Siehe hier zur Veranschaulichung von Ultraspherical-Fenster mit unterschiedlicher Parametrisierung.








![{\displaystyle w(n)={\frac {1}{2}}\left[1-\cos \left({\frac {2\pi n}{M-1}}\right)\right]=\operatorname {hvs} \left({\frac {2\pi n}{M-1}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0ce27c6d8d18a9b1c6bc2d6a734b450acf8ceea)

![{\displaystyle w(n)={\frac {1}{2}}\left[1+\cos \left({\frac {2\pi n}{M-1}}\right)\right]=\operatorname {hvc} \left({\frac {2\pi n}{M-1}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efe4df346a4c497a96a3d74ddc0d01192a0b869e)

























![{\displaystyle w(n)={\begin{cases}{\frac {1}{2}}\left[1+\cos \left(\pi \left({\frac {2n}{\alpha (M-1)}}-1\right)\right)\right]=\operatorname {hvc} \left(\pi \left({\frac {2n}{\alpha (M-1)}}-1\right)\right),&{\text{wenn }}0\leq n\leq {\frac {\alpha (M-1)}{2}},\\1,&{\text{wenn }}{\frac {\alpha (M-1)}{2}}\leq n\leq (M-1)(1-{\frac {\alpha }{2}}),\\{\frac {1}{2}}\left[1+\cos \left(\pi \left({\frac {2n}{\alpha (M-1)}}-{\frac {2}{\alpha }}+1\right)\right)\right]=\operatorname {hvc} \left(\pi \left({\frac {2n}{\alpha (M-1)}}-{\frac {2}{\alpha }}+1\right)\right),&{\text{wenn }}(M-1)(1-{\frac {\alpha }{2}})\leq n\leq (M-1).\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260031252ad49bcd3605f5de5c85d0415a37060d)

![{\displaystyle w(n)={\frac {I_{0}\left(\alpha \left[1-\left({\frac {2n}{M}}\right)^{2}\right]^{\frac {1}{2}}\right)}{I_{0}\left(\alpha \right)}},\quad n=-{\frac {M}{2}},\dotsc ,{\frac {M}{2}}-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6960c88e5eab960a4b5a395ae4eb7484af8dc5da)






![{\displaystyle A_{\mathrm {SL} }=20\cdot \log _{10}\left[{\frac {\sinh \alpha }{0{,}217234\alpha }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7dd4a09658269036a350a182efda74e75e78619)


![{\displaystyle w[n]={\frac {1}{N+1}}\left[C_{N}^{\mu }(x_{0})+\sum _{k=1}^{\frac {N}{2}}C_{N}^{\mu }\left(x_{0}\cos {\frac {k\pi }{N+1}}\right)\cos {\frac {2n\pi k}{N+1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5e8dc43d2c5edbe601e3abf542a177689f4276)















