Gleitender Mittelwert
Der gleitende Durchschnitt (auch gleitender Mittelwert) ist eine Methode zur Glättung von Zeit- bzw. Datenreihen. Die Glättung erfolgt durch das Entfernen höherer Frequenzanteile. Im Ergebnis wird eine neue Datenpunktmenge erstellt, die aus den Mittelwerten gleich großer Untermengen der ursprünglichen Datenpunktmenge besteht. In der Signaltheorie wird der gleitende Durchschnitt als Tiefpassfilter mit endlicher Impulsantwort (FIR-Tiefpass) beschrieben. In der gleichgewichteten Form stellt der gleitende Durchschnitt das einfachste FIR-Tiefpassfilter dar.
Anwendung findet der gleitende Durchschnitt beispielsweise bei der Analyse von Zeitreihen. Die gleichgewichtete Variante entspricht der Faltung mit einer Rechteckfunktion und führt zu einer Reihe von Problemen, denen beispielsweise mit speziellen Gewichtungen entgegengewirkt werden kann.
Prinzipielles Vorgehen[Bearbeiten | Quelltext bearbeiten]
Die Menge der gleitenden Durchschnitte wird iterativ („gleitend“) über einen Ausschnitt, das „Fenster“, eines gegebenen Signals berechnet. Das verwendete Fenster wird überlappend verschoben, d. h., wiederholt wird der letzte Wert aus dem betrachteten Ausschnitt gestrichen, der erste Wert nach dem Ausschnitt hinzugenommen und ein neuer Mittelwert berechnet. Für die Berechnung des Mittelwerts können die im Fenster vorkommenden Werte anschließend beliebig gewichtet werden.
Die Ergebnismenge der Mittelwerte ist für sich genommen unabhängig. Häufig wird sie jedoch in den Zusammenhang mit einer Position der Eingabemenge gebracht, die „hot spot“ genannt wird. Der hot spot kann im Bereich des Fensters liegen, muss es aber nicht. Bei Zeitreihen wird häufig der letzte Zeitpunkt als hot spot verwendet; in anderen Anwendungsfällen sind zentrierte Abbildungen üblich.
Einfacher gleitender Durchschnitt[Bearbeiten | Quelltext bearbeiten]
Berechnung und Zentrierung der Berechnung[Bearbeiten | Quelltext bearbeiten]

Der einfache gleitende Durchschnitt (englisch simple moving average (SMA)) -ter Ordnung einer diskreten Zeitreihe ist die Folge der arithmetischen Mittelwerte von aufeinanderfolgenden Datenpunkten. Da es sich um eine Zeitreihe handelt, liegt der hot spot auf dem letzten Zeitpunkt. Die nachfolgenden Ausführungen beziehen sich auf diesen Sonderfall.
In Analogie zu Filtern mit endlicher Impulsantwort wird auch Ordnung genannt.
Solch ein gleitender Durchschnitt hat eine Verzögerung (Gruppenlaufzeit) von , d. h. die gemittelten Werte „hinken“ um Zeiteinheiten hinterher.
Diese Verzögerung kann korrigiert werden, indem man den gleitenden Durchschnitt um verschiebt. Dies ist der sogenannte zentrierte Durchschnitt. Dann sind jedoch keine Werte mehr für die ersten und letzten Zeiteinheiten vorhanden. Ohne den Einsatz eines dynamischen Fensters kann diese Lücke nur geschlossen oder zumindest verkleinert werden, indem man eine geringere Ordnung, andere Gewichtungen oder einen Schätzer verwendet.
Der zentrierte einfache gleitende Durchschnitt der Ordnung 3 ist also durch
gegeben.
Ein Beispiel für die Verwendung von derartigen gleitenden Durchschnitten sind die 38- bzw. 200-Tage-Durchschnittswerte von Börsenkursen, die den gleitenden Durchschnitt der vergangenen Börsentage eines Wertpapierkurses beschreiben.
Ein Gleitender-Mittelwert-Filter ist ein Tiefpass-Filter, jedoch werden einzelne Frequenzbereiche stärker oder schwächer gefiltert, und es kommt zu Signalverschiebungen (englisch Lags).

Gleitender Durchschnitt mit dynamischem Fenster[Bearbeiten | Quelltext bearbeiten]
Der gleitende Durchschnitt -ter Ordnung einer diskreten Menge mit Elementen hat Wertepaare weniger als die Gesamtmenge. Da sehr stark oszillierende Graphen eine entsprechend hohe Ordnung zur ausreichenden Glättung der Ergebnismenge benötigen, kann dieser Effekt einen spürbaren Einfluss auf die Darstellung haben. Die resultierende Trendlinie liegt dann bei nicht zentriertem einfachen gleitenden Durchschnitt verstärkt versetzt und gibt somit eine zunehmend schlechtere Abstraktion der Originaldaten wieder.
Bei einer diskreten Menge kann der Versetzungseffekt durch die Verwendung eines dynamischen Mittelwertfensters vermieden werden. Bei diesem Verfahren wird jeder Mittelwert aus den Parametern bis berechnet. Die Fensterränder und leiten sich aus der jeweiligen relativen Position ab, mit:
ist dabei die (absolute) Position von in . Das mit Hilfe von und definierte dynamische Fenster zur Bildung der Mittelwerte deckt die volle Breite des ursprünglichen Graphen ab und abstrahiert die Originaldaten von Rundungsfehlern abgesehen versetzungsfrei. Geometrisch wird die Position des Elements in der Gesamtmenge auf die Position des Elements in der Auswahlmenge abgebildet. Randelemente landen im entsprechenden Rand, das zentrale Element der Gesamtmenge liegt auch im Auswahlintervall mittig. Je mittiger das Element umso geringer der Versatz.
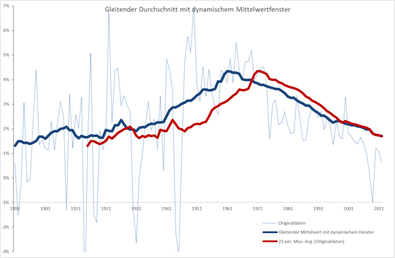
Beispiel
Das Wachstum der volkswirtschaftlichen Produktivität zwischen 1891 und 2012 schwankt sehr stark. Der Graph gebildet aus dem gleitenden Mittelwert der Ordnung glättet diese Kurve gut (rote Linie).
Berechnungsbeispiel für den ersten möglichen Wert von 1915
Die geglättete Kurve ist eine zwar aussagekräftige, aber deutlich versetzte Trendlinie. Zudem gehen dabei gut 20 % der Wertepaare verloren. Mit Hilfe eines dynamischen Fensters lassen sich die Werte über die gesamte Breite von berechnen. Das Ergebnis ist eine besonders im Inneren des Untersuchungszeitraums kaum versetzte Trendlinie (blaue Linie).
Berechnungsbeispiel für 1891, 1915 und 2012
Die Menge hat 122 Elemente: , 1891 ist der Zeitindex des ersten Elements und .
Damit folgen und und es wird das Intervall bis betrachtet (die anderen Werte analog).
Online-Berechnung[Bearbeiten | Quelltext bearbeiten]
Durch die Überlappung bei der Berechnung des gleitenden Mittels für zwei aufeinanderfolgende Punkte wird die Summe für Punkte doppelt berechnet. Um diesen redundanten Aufwand zu reduzieren, existiert ein Online-Algorithmus, der mit nur zwei Additionen und Multiplikationen pro Mittelwert auskommt:
Gewichteter gleitender Durchschnitt[Bearbeiten | Quelltext bearbeiten]
Der gewichtete gleitende Durchschnitt der Ordnung einer Zeitreihe ist – analog zum Filter mit endlicher Impulsantwort – definiert als:
Dabei stellt die Gewichtung der jeweiligen Datenpunkte dar (äquivalent zur Impulsantwort des Filters). Wenn , ist das Filter nicht kausal, sondern berücksichtigt zukünftige Werte bei der Durchschnittsbildung. Die Summe über alle Gewichte muss 1 ergeben, da sonst noch eine Verstärkung () oder Dämpfung () hinzukommt.
Ein Beispiel ist das zentrierte Binomialfilter dritter Ordnung mit , , und :
Zentrierter gleitender Durchschnitt mit spektralen Eigenschaften[Bearbeiten | Quelltext bearbeiten]

Bildet man den zentrierten gleitenden Durchschnitt -ter Ordnung einer schwach stationären Zeitreihe mit Spektraldichte , dann hat die gefilterte Spektraldichte
mit der Übertragungsfunktion
- ,
wobei den Fejér-Kern bezeichnet. An der grafischen Darstellung für mit der Übertragungsfunktion kann man die Tiefpass-Eigenschaft erkennen: Frequenzen nahe 0 werden nicht gedämpft. Andererseits zeigt dieses einfache Filter das übliche Antwortverhalten bei der Faltung mit einem Rechtecksignal. Bei einer Filterbreite von 3 werden die Frequenzen bis zum Punkt zunehmend bis zur vollständigen Unterdrückung gedämpft. Frequenzen, die über diesen Punkt hinaus vorhanden sind, werden nicht etwa auch unterdrückt, sondern treten mit invertierter Phase auf.
Das kleinste Binomialfilter mit ungerader Breite und mit den Gewichten , , ist ein Tiefpass-Filter mit für alle Frequenzen. Es dämpft die Frequenzen bis zunehmend und mit konstanter Phasenverschiebung.[1]

Linear gewichteter gleitender Durchschnitt[Bearbeiten | Quelltext bearbeiten]
Ein linear gewichteter gleitender Durchschnitt (engl.: linear weighted moving average (LWMA, meist: WMA)) ordnet den Datenpunkten linear aufsteigende Gewichte zu, d. h. je weiter die Werte in der Vergangenheit liegen, desto geringer ist ihr Einfluss:
Exponentiell geglätteter Durchschnitt[Bearbeiten | Quelltext bearbeiten]
Der exponentiell geglättete Durchschnitt ordnet den Datenpunkten einer Zeitreihe exponentiell abnehmende Gewichte zu. Somit werden auch hier jüngere Datenpunkte stärker gewichtet als weiter zurückliegende, jedoch noch stärker als beim gewichteten gleitenden Durchschnitt.
Da der exponentielle Durchschnitt nicht nur Werte aus der Zeitreihe, sondern auch vorangegangene Mittelwerte miteinbezieht, stellt er ein Filter mit unendlicher Impulsantwort dar. Ein entscheidender Vorteil ist seine wesentlich kürzere Verzögerung bei gleicher Glättung.
Exponentiell gewichteter geglätteter Durchschnitt[Bearbeiten | Quelltext bearbeiten]
Der exponentiell gewichtete geglättete Durchschnitt (EMWA) ist eine Verallgemeinerung des exponentiell geglätteten Durchschnitts, wobei Gewichte eingeführt werden.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- John G. Proakis, Dimitris G. Manolakis: Digital Signal Processing. 4. Auflage. Prentice Hall, 2007, ISBN 978-0-13-187374-2.
Weblinks[Bearbeiten | Quelltext bearbeiten]
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Jens-Peter Kreiß, Georg Neuhaus: Einführung in die Zeitreihenanalyse. Springer, 2006, ISBN 3-540-25628-8.






























































