Gruppenlaufzeit

Unter der Gruppenlaufzeit $\tau _{\mathrm {gr} }$ (englisch group delay) eines schmalbandigen Signals durch ein LZI-System (z. B. durch ein elektronisches Filter oder einen Übertragungskanal) versteht man die Verzögerung der Umhüllenden dieses Signals.

Veranschaulichung und Bedeutung

Gruppenlaufzeit τ_gr beim Durchlaufen eines Filters

Die rechte Abbildung zeigt eine Wellengruppe vor bzw. nach dem Durchlauf durch ein LZI-System (im Folgenden kurz „System“) wie z. B. ein elektronisches Filter oder eine Übertragungsstrecke. Die sogenannte Einhüllende ist als blau gestrichelte Linie eingezeichnet, die Trägerfrequenz in violett und die Gruppenlaufzeit zwischen Eingangs- und Ausgangssignal mit $\tau _{\mathrm {gr} }$ bezeichnet. Die Gruppenlaufzeit korreliert mit dem zeitlichen Versatz der Einhüllenden.

Die Durchlaufzeit einer Wellengruppe durch ein System hängt von den Eigenschaften des Systems und von der Trägerfrequenz der Wellengruppe ab. Die Gruppenlaufzeit besitzt oft eine nicht lineare Abhängigkeit von der Frequenz. Ist die Gruppenlaufzeit jedoch konstant, dann ist die Durchlaufzeit verschiedener Wellengruppen zu unterschiedlichen Frequenzen gleich. D. h. beim Passieren des Systems erfahren alle Wellengruppen die gleiche Verzögerung, weshalb die relative Lage der Gruppen zueinander erhalten bleibt. Aus diesem Grund „zerfließt“ ein Breitbandsignal beim Passieren eines solchen Systems nicht. In Anlehnung an die optische Physik tritt quasi keine Dispersion auf.

Besitzt ein System einen linearen Phasengang, dann weist es eine konstante Gruppenlaufzeit auf.

Eine konstante Gruppenlaufzeit ist z. B. bei Übertragungsstrecken erwünscht, damit der Phasenverlauf eines zu übertragenden Nutzsignales bei der Übertragung möglichst erhalten bleibt. Die Übertragungsfunktion eines Koaxialkabels besitzt beispielsweise in guter Näherung einen linearen Phasengang und damit eine konstante Gruppenlaufzeit.

Definition

Betrag und Phasengang eines Bandpasssystems

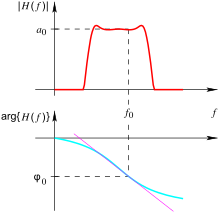
Dem System soll eine Übertragungsfunktion $H(s)|_{s=j\omega }=H(j\omega )$ mit Betragsfrequenzgang $|H(j\omega )|$ und Phasengang $\varphi (\omega )$ zugrunde liegen, so dass gilt:

$H(j\omega )=|H(j\omega )|\cdot \exp(j\varphi (\omega ))$

Bzw.:

$\varphi (\omega ):=\arg\{H(j\omega )\}$

Die Gruppenlaufzeit ergibt sich aus dem Phasengang durch:

$\tau _{\mathrm {gr} }(\omega )=-{\frac {\mathrm {d} \varphi (\omega )}{\mathrm {d} \omega }}$

Bei gegebener Übertragungsfunktion im Laplacebildbereich kann die Gruppenlaufzeit auch direkt (ohne den Umweg über die Phasendarstellung) berechnet werden:

$\tau _{\mathrm {gr} }(\omega )=\Re \left.\left\{-{\frac {dH(s)/ds}{H(s)}}\right\}\right|_{s=j\omega }$

Mathematische Beschreibung

Zur Herleitung der Gruppenlaufzeit studiert man die Antwort eines Systems auf die Anregung mit einem Signal in der Form einer Wellengruppe. Das anregende Signal soll ebenso wie die Antwort des Systems reell, also nicht komplex sein. Die Wellengruppe kann man als Produkt einer reellen Einhüllenden mit einer reellen harmonischen Festfrequenz (Trägerfrequenz) (be-)schreiben:

$u_{1}(t)=u_{e}(t)\cos(\omega _{0}t)$

Das zugehörige Amplitudendichtespektrum lautet

$U_{1}(\omega )={\frac {1}{2}}(U_{e}(\omega -\omega _{0})+U_{e}(\omega +\omega _{0}))$

Der Betragsfrequenzgang der Einhüllenden $|U_{e}(\omega )|$ soll dabei auf einen hinreichend kleinen Frequenzbereich $|\omega |\leq \omega _{1}$ beschränkt sein und außerhalb dieses Bereiches hinreichend schnell verschwinden. Hinreichend klein und schnell bedeutet in diesem Zusammenhang, dass der Betragsfrequenzgang der Übertragungsfunktion $H(i\omega )$ bzw. der Phasenverlauf $\varphi (\omega )$ in den Bereichen $\omega =\omega _{0}\pm \omega _{1}$ und $\omega =-\omega _{0}\pm \omega _{1}$ hinreichend gut durch lineare Funktionen angenähert werden kann.

Für Systeme mit reeller Impulsantwort $h(t)$ ist der Betragsfrequenzgang eine gerade Funktion in $\omega$. In den Bereichen um $\omega =\pm \omega _{0}$ gilt daher näherungsweise:

$|H(j\omega )|={\text{const}}$

Für Systeme mit reeller Impulsantwort $h(t)$ ist die Phase eine ungerade Funktion in $\omega$. In den Bereichen um $\omega =\pm \omega _{0}$ gilt daher näherungsweise:

$\varphi (\omega )=\left\{{\begin{array}{lc}a+b(\omega -\omega _{0})&\mathrm {f{\ddot {u}}r} \quad \omega >0\\-a+b(\omega +\omega _{0})&\mathrm {f{\ddot {u}}r} \quad \omega <0\,\end{array}}\right.$

Die Konstanten $a$ und $b$ erhält man durch Taylorentwicklung des Phasenganges. Konkret gilt $b=\left.{\frac {d\varphi }{d\omega }}\right|_{\omega =\pm \omega _{0}}$.

Durch Anwenden der Übertragungsfunktion im Frequenzbereich auf die Wellengruppe und durch Fourier-Rücktransformation unter den gemachten Voraussetzungen erhält man am Ausgang des Systems die Antwort:

$u_{2}(t)={\text{const}}\cdot u_{e}(t+b)\cos(\omega _{0}t+a)$

Man erkennt am Argument der Einhüllenden, dass $b$ mit der Laufzeit der Gruppe im Zusammenhang steht. Mit der Definition der Gruppenlaufzeit

$\tau _{\mathrm {gr} }(\omega )=-{\frac {d\varphi (\omega )}{d\omega }}$

identifiziert man $b=-\tau _{\mathrm {gr} }(\pm \omega _{0})$. Damit ist die Einhüllende der Gruppe genau um eine Gruppenlaufzeit nach Passieren des Systems verzögert.

Die Gruppenlaufzeit ist von der Phasenlaufzeit zu unterscheiden. In diesem Beispiel beträgt die Phasenlaufzeit:

$\tau _{\mathrm {ph} }(\pm \omega _{0})=-\left.{\frac {\varphi (\omega )}{\omega }}\right|_{\omega =\pm \omega _{0}}=-{\frac {a}{\omega _{0}}}$

Beispiele

Tiefpass erster Ordnung

Es soll die Gruppenlaufzeit eines Tiefpasses (lineares kontinuierliches System erster Ordnung) angegeben werden. Dieses System kann beispielsweise als ein RC-Glied implementiert werden. Aus dem Frequenzgang

$H(j\omega )={\frac {1}{j{\frac {\omega }{\omega _{3\mathrm {dB} }}}+1}}$

ergibt sich der Phasengang zu:

$\varphi (\omega )=-\arctan \left({\frac {\omega }{\omega _{3\mathrm {dB} }}}\right)$

Dabei ist $\omega _{3\mathrm {dB} }$ eine filterabhängige Konstante. Die Gruppenlaufzeit für diesen Tiefpassfilter ergibt sich zu:

$\tau _{\mathrm {gr} }(\omega )=-{\frac {d}{d\omega }}\left[-\arctan \left({\frac {\omega }{\omega _{3\mathrm {dB} }}}\right)\right]={\frac {1}{\omega _{3\mathrm {dB} }}}{\frac {1}{1+({\frac {\omega }{\omega _{3\mathrm {dB} }}})^{2}}}$

Akustik

Eine möglichst frequenzunabhängige Gruppenlaufzeit ist auch in der Elektroakustik, insbesondere für eine naturgetreue Tonwiedergabe, von Wichtigkeit. Viele Komponenten einer Audiowiedergabekette, wie beispielsweise die Lautsprecher-Frequenzweichen (Crossover), verändern die Gruppenlaufzeit des Signals. Aber auch die Architektur von Hörräumen hat hier erheblichen Einfluss. Akustische Resonatoren können die Gruppenlaufzeit ebenso beeinflussen wie Komponenten von Lautsprecheranlagen. Hierbei ist es wichtig, die Wahrnehmungsschwelle für die Hörbarkeit von Gruppenlaufzeitänderungen als Funktion der Frequenz zu kennen, speziell, wenn die Audiokette für die Hi-Fi-Wiedergabe vorgesehen ist. Tabellen sind bei Blauert und Laws zu finden:

Frequenz	Hörbarkeitsschwelle
500 Hz	3,2 ms
1 kHz	2 ms
2 kHz	1 ms
4 kHz	1,5 ms
8 kHz	2 ms

Literatur

• Athanasios Papoulis: The Fourier Integral and Its Applications. McGraw-Hill, New York [u. a.] 1962, ISBN 0-07-048447-3 (Auch ohne ISBN erschienen).
• Karl-Dirk Kammeyer: Nachrichtenübertragung. 3. Auflage. Teubner Verlag, Leipzig Wiesbaden 2004, ISBN 3-519-26142-1.
• Norbert Fliege: Systemtheorie. Teubner Verlag, Stuttgart 1982, ISBN 3-519-06140-6.

Weblinks

• Grafiken zur Gruppenlaufzeitmessung bei Lautsprechern

Einzelnachweise

Wellengeschwindigkeiten

Phasengeschwindigkeit	Gruppengeschwindigkeit	Signalgeschwindigkeit
Phasenlaufzeit	Gruppenlaufzeit	Signallaufzeit