Rot-Schwarz-Baum
| Rot-Schwarz-Baum | ||
|---|---|---|
| Komplexität bei Elementen | ||
| Platz | ||
| Operation | im Mittel, amortisiert |
Worst Case |
| Suchen | ||
| Querschritt | ||
| Min, Max | ||
| Einfügen | † | |
| Löschen | † | |
† ohne Navigation (nur Rebalancierung) | ||
| Platz- und Zeit-Komplexitäten | ||
Ein Rot-Schwarz-Baum, auch RS-Baum oder RB-Baum, (englisch red–black tree oder RB tree) ist eine Datenstruktur vom Typ binärer Suchbaum, die „sehr schnellen“ Zugriff auf die in ihr gespeicherten Schlüssel garantiert. Rot-Schwarz-Bäume wurden zuerst 1972 von Rudolf Bayer beschrieben,[1] welcher sie symmetric binary B-trees nannte. Der heutige Name geht auf Leonidas J. Guibas und Robert Sedgewick zurück, die 1978 die rot-schwarze Farbkonvention einführten.[2] Die schnellen Zugriffszeiten auf die einzelnen im Rot-Schwarz-Baum gespeicherten Elemente (meist Paare vom Typ (Schlüssel,Wert)) werden durch zwei Forderungen erreicht, die die Balance des Baums in einer Weise festlegen, dass die Höhe eines Baums mit Elementen nie größer als sein kann.[Anm. 1] Somit können die wichtigsten Operationen in Suchbäumen – Suchen, Einfügen und Löschen – garantiert in (s. Landau-Symbole) ausgeführt werden.
Definition[Bearbeiten | Quelltext bearbeiten]
Zusätzlich zu den Eigenschaften des binären Suchbaums hat jeder Knoten des Rot-Schwarz-Baums ein weiteres Attribut, genannt »Farbe«, das zwei Werte annehmen kann, genannt »rot« (RED) und »schwarz« (BLACK). Diese Einfärbung hat die folgenden zwei Forderungen zu erfüllen:[3]
|
Ein Kindknoten eines roten Knotens ist schwarz. |
|
Jeder Pfad von einem gegebenen Knoten zu einem seiner Nachfahren mit Ausgangsgrad ≤1, d. h. zu Blättern oder Halbblättern, im Folgenden kurz Pfadenden genannt,[4] enthält die gleiche Anzahl schwarzer Knoten. |

der Baumhöhe 4 und der Schwarzhöhe 2
Eine unmittelbare Folge aus den Forderungen ist, dass ein Halbblatt (bspw. der Knoten im Beispielbaum) schwarz und sein (einzelnes) Kind (der Knoten ) rot sein muss, denn beide sind Pfadenden, und der Pfad zum Pfadende links ist um genau den Knoten kürzer.
Aus beiden Forderungen zusammen folgt ähnlich unmittelbar, dass ein schwarzer Knoten, der nicht die Wurzel ist, ein Geschwister hat.
Schwarzhöhe, Baumhöhe[Bearbeiten | Quelltext bearbeiten]
Die auf allen Pfaden von Pfadende zu Wurzel gleiche Anzahl schwarzer Knoten wird die »Schwarzhöhe« (englisch black height)[5][6] genannt: des Baums, aber auch seiner Wurzel. Nach dieser Definition ist ein Knoten der Schwarzhöhe 0 ein rotes Blatt (dann ist seine Baumhöhe 1) wie bspw. die Knoten im Beispielbaum – oder ein unechter (und leerer) Knoten mit der Baumhöhe 0. In diesem Artikel sind schwarze Knoten echt (und Schlüssel tragend) und haben sowohl Schwarzhöhe wie Baumhöhe ≥ 1. Die roten Knoten aber auch die schwarzen Knoten haben Schwarzhöhe 1. Die schwarzen Knoten haben Baumhöhe 2, die Knoten Baumhöhe 1, und ist der einzige Knoten mit Ausgangsgrad 1, das einzige Halbblatt.
Durch die zwei Forderungen[7] wird die wichtigste Eigenschaft von Rot-Schwarz-Bäumen sichergestellt:
Ist die Schwarzhöhe des Baums, dann gibt es wegen der Forderung S#= auf einem Pfad von der Wurzel zu einem Pfadende genau schwarze Knoten, aber wegen der Forderung !RR höchstens einen roten Knoten mehr als schwarze, also insgesamt maximal Knoten. Damit gilt für die Zahl aller Knoten im Baum , so dass der Rot-Schwarz-Baum immer gut genug balanciert ist – auf jeden Fall so gut, dass das Verhältnis zwischen der Baumhöhe für die gilt, und dem Logarithmus der Knotenzahl beschränkt bleibt. Diese logarithmische Beschränkung, die im Abschnitt Höhenbeweis formal bewiesen wird, ist aber gleichzeitig das informationstheoretische Optimum, d. h. es gibt keinen Binärbaum mit kleinerer maximaler Pfadlänge
Bei den herausgehobenen Operationen Suchen, Einfügen und Löschen ist der auf einer Ebene des Baums anfallende Aufwand konstant. Also ist die Laufzeit höchstens proportional zur Anzahl der Knoten in einem Pfad, die wieder durch die Höhe limitiert ist, welche ihrerseits durch den Logarithmus der Knotenzahl limitiert ist.
NIL-Knoten[Bearbeiten | Quelltext bearbeiten]
Dieser Artikel nimmt die im Artikel Binärer Suchbaum in dessen Abb. 1A aufgezeigte und bei vielen Baumstrukturen übliche Sichtweise ein, bei der die Knoten die Schlüssel tragen (knotenorientierte Speicherung), unabhängig davon, ob sie interne Knoten oder (interne) Blätter sind.

(Baum- und Schwarzhöhe sind 4 und 2 – wie oben)
Sehr verbreitet in der Literatur über Rot-Schwarz-Bäume ist die nebenstehende und im Artikel Binärer Suchbaum in dessen Abb. 1B gezeigte Sichtweise, bei der – ebenfalls knotenorientiert – die die Schlüssel tragenden Knoten als intern angesehen werden, dem Baum aber zusätzliche Knoten, so genannte »NIL-Knoten«, als externe Blätter angeheftet sind, die an den Pfadenden für die (randlosen, „offenen“) Intervalle (englisch auch missing nodes[8]) zwischen den Schlüsseln stehen. Die Darstellung mit NIL -Knoten bringt das einseitige Pfadende links (links am Knoten ) ähnlich deutlich heraus wie die paarigen Pfadenden an den Knoten Völlig unabhängig von der grafischen Darstellung lassen sich die NIL-Knoten sowohl als unterschiedslose Nullzeiger wie als unterschiedslose Zeiger zu ein und demselben Wächterknoten implementieren.
Diese Option beim Zeigerwert wird zur Unterscheidung vom Nullzeiger im Text als NIL-Zeiger oder NIL und im Beispielcode als NIL kenntlich gemacht.
Werden die NIL-Knoten jedoch als individuelle Knoten aufgefasst, dann kommt für sie eine Forderung hinzu, so dass folgende drei Forderungen aufzustellen sind:[9]:273
- NIL-Knoten sind schwarz.
- Kinder eines roten Knotens sind schwarz.
- Die Anzahlen schwarzer Knoten in einem Pfad von einem gegebenen Knoten zu jedem seiner NIL-Knoten sind gleich.
Diese Auffassung hat für das Verständnis der Sachverhalte vernachlässigbaren Nutzen und hat bei „naiver“ Implementierung eher einen ungünstigen Einfluss.[Anm. 2]
Datenstruktur[Bearbeiten | Quelltext bearbeiten]
Der nachfolgende Beispielcode, der in der Programmiersprache C formuliert ist, nimmt Bezug auf eine Deklaration des Baumknotens der folgenden Art:
struct RBnode // Knotenfeld
{
struct RBnode* child[2]; // Zeiger zu ≤2 Kindknoten dieses Knotens
// oder NIL: kein Kindknoten
byte color; // RED oder BLACK
... // Benutzer-Daten (z. B. Schlüssel, Wert)
} ;
#define LEFT 0
#define RIGHT 1
#define left child[LEFT] // -> linker Kindknoten
#define right child[RIGHT] // -> rechter Kindknoten
#define RED 0
#define BLACK 1
Befindet sich NIL an einer Stelle im Baum, an der syntaktisch ein Zeiger zu einem Knoten erwartet wird, so soll dies verabredungsgemäß das Fehlen eines Knotens (einen Null- oder auch Wächterknoten) an dieser Stelle des Baums bedeuten (der Knoten gilt als unecht). M. a. W.: der von einem NIL-Knoten gewurzelte Teilbaum ist leer und hat Schwarz- und Baumhöhe 0.
Sein Zeigerwert X == NIL ist weniger wichtig als der Ort, wo dieser Wert in der Datenstruktur steht. Dieser Ort gibt die graphentheoretischen Beziehungen zu den anderen Elementen des Baums an:
- Ohne selbst einen Knoten zu repräsentieren, kann er in Kindesbeziehung, und damit auch in Geschwister- und Onkelbeziehung zu anderen Knoten stehen – niemals aber ein Elter sein.
Seine Baumhöhe und Schwarzhöhe gelten beide als 0, und Farbe ist ihm auch nicht zugeordnet. Er hat einen Elter (wenn er die Wurzel ist, den Baum als logischen Elter), aber niemals einen Zeiger zum Elter.
Funktionell entspricht er exakt dem NIL-Knoten, ohne dass ihm allerdings irgendeine Individualität zukäme.
Werden der Datenstruktur Rot-Schwarz-Baum Operationen zum Zugriff und zur Verwaltung beigegeben, so werden diese nur dann als zugehörig angesehen, wenn sie die Rot-Schwarz-Forderungen aufrechterhalten, indem sie insbesondere den Baum nach einer modifizierenden Operation überprüfen und wenn nötig reparieren. So erweitert wird die Datenstruktur zu einem Abstrakten Datentyp (ADT). Bei Suchbäumen gibt es im Englischen dafür auch die Charakterisierung als self-balancing tree.
[Bearbeiten | Quelltext bearbeiten]
Die Navigationsoperationen, das sind die verschiedenen Suchoperationen, das Traversieren, Aufsuchen erstes oder letztes Element und ähnliche, lassen den Baum unverändert (nur lesender Zugriff) und funktionieren im Prinzip auf jedem binären Suchbaum. Die dortigen Algorithmen und Angaben zur Komplexität gelten genauso für Rot-Schwarz-Bäume – mit der Präzisierung, dass die Höhe des Rot-Schwarz-Baums sich immer logarithmisch zur Anzahl der Knoten verhält.
Das Suchen eines Elements (oder einer Lücke) anhand seines Schlüssels ist die wichtigste unter den Navigationsoperationen. (Die (Höhen-)Balancierung des Rot-Schwarz-Baums versucht, auf diese Operation hin zu optimieren.) Sie unterstützt eine Art direkten Zugriff (im Gegensatz zum sequentiellen Zugriff der Traversierung) und wird in der Regel als vorausgehende Operation bei den Modifikationsoperationen (Einfügen oder Löschen) zum Auffinden der betreffenden Stelle im Baum eingesetzt.
Das Suchen setzt eine totale Quasiordnung auf der Menge der Schlüssel voraus, die am flexibelsten durch eine Vergleichsfunktion realisiert wird. Wenn Duplikate im Baum erlaubt sein sollen, dann empfiehlt sich eine leicht abgewandelte Suchfunktion.
Zeichenerklärung zu den Diagrammen[Bearbeiten | Quelltext bearbeiten]
Die komplizierteren Einzelfälle der Einfüge- und Löschoperation werden weiter unten in Diagrammen skizziert. Diese Diagramme stellen die für die Rebalancierung relevanten Beziehungen und Farben von Knoten heraus.
Ein Diagramm hat drei Spalten, wobei die linke Spalte die Überprüfung auf der untersten Stufe (ersten Iteration) eines Falles und die rechte die auf einer höheren Ebene desselben Falles beschreibt. Die mittlere Spalte unterteilt die Transformation in mindestens zwei Abschnitte:
- Der erste (und oberste, mit »Bedingung« beschriftete) Abschnitt zeigt die Ausgangskonstellation,
- eine eventuelle »Rotation« folgt im nächsten Schritt,
- danach eine »Umfärbung«, falls erforderlich.
- Wenn der Baum dann noch nicht rebalanciert ist, zeigt der letzte (mit »Neuzuweisung« beschriftete) Abschnitt die Konstellation nach der erneuten Zuweisung des Problemknotens und der durch ihn bestimmten anderen Knoten. Diese Konstellation wird zur Weiterbehandlung an den in der Spalte →Test eingetragenen Fall übergeben.
Die erste Iterationsstufe spielt sich auf der tiefstmöglichen Ebene des Baums ab. Dies gilt für Einfügungen wie auch erstaunlicherweise für Löschungen. Da Schwarzhöhen und Baumhöhen auf sie bezogen werden können, soll diese Iterationsstufe auch einen Namen als Variable haben, und zwar den Buchstaben mit dem ersten Wert mit der Folge, dass in den komplizierteren Fällen der Problemknoten in der ersten Iterationsstufe die Schwarzhöhe und in den höheren hat.
Obwohl die Konstellation der untersten Stufe in denen der höheren im Prinzip enthalten ist, werden die sie betreffenden Diagramme um der größeren Deutlichkeit willen gebracht, und zwar ohne leere Teilbäume.
Beim Löschen wird in der untersten Stufe das Pfadende, das einen schwarzen Knoten verloren hat (und das dem Problemknoten entspricht, der hier leer ist), durch einen blauen Pfeil nach links ![]() markiert.
markiert.
- Der alte Problemknoten ( im Abschnitt »Bedingung« eines Diagramms) hat eine blaue Kontur; und wenn die Operation nicht beendet ist, dann auch der neue (im Abschnitt »Neuzuweisung«).
- Das Symbol
 stellt einen (echten) schwarzen und
stellt einen (echten) schwarzen und  einen (echten) roten Knoten dar.
einen (echten) roten Knoten dar. - Das Symbol
 stellt einen !RR-konform bei seinem Elter angebundenen Teilbaum dar. Er hat (außer in den Abschnitten »Neuzuweisung«) die Schwarzhöhe . Die Schwarzhöhe ist in der ersten Iterationsstufe 0; dann besteht der Teilbaum entweder
stellt einen !RR-konform bei seinem Elter angebundenen Teilbaum dar. Er hat (außer in den Abschnitten »Neuzuweisung«) die Schwarzhöhe . Die Schwarzhöhe ist in der ersten Iterationsstufe 0; dann besteht der Teilbaum entweder
- aus einem roten Blatt oder
- er ist leer, also ein NIL-Knoten, wann der „Knoten“ auch als unecht gilt.
- Das Dreieck
 (ohne die kleine schwarze Kreisfläche an der Spitze) symbolisiert einen !RR-konform bei seinem Elter angebundenen Teilbaum, dessen Schwarzhöhe ist. Seine Schwarzhöhe ist also um 1 niedriger als die der
(ohne die kleine schwarze Kreisfläche an der Spitze) symbolisiert einen !RR-konform bei seinem Elter angebundenen Teilbaum, dessen Schwarzhöhe ist. Seine Schwarzhöhe ist also um 1 niedriger als die der  -Teilbäume. In der ersten Iterationsstufe wäre die Schwarzhöhe negativ, was so zu interpretieren ist, dass schon sein Elter leer ist.
-Teilbäume. In der ersten Iterationsstufe wäre die Schwarzhöhe negativ, was so zu interpretieren ist, dass schon sein Elter leer ist. - Zweimal
 in einem Diagramm oder auf einer Zeile der Zusammenschau bedeutet zweimal dieselbe Knotenfarbe, schwarz oder rot.
in einem Diagramm oder auf einer Zeile der Zusammenschau bedeutet zweimal dieselbe Knotenfarbe, schwarz oder rot.
Operation Einfügen[Bearbeiten | Quelltext bearbeiten]
Die ersten Aktionen beim Einfügen eines neuen Knotens in einen Rot-Schwarz-Baum unterscheiden sich nicht von denen eines allgemeinen binären Suchbaums: Der Zeiger zum neuen Knoten ersetzt einen NIL-Zeiger, der an einem Pfadende steht und als Indikator für das Fehlen entweder der Wurzel, falls der Baum leer ist, oder – bei einem Schlüssel tragenden Knoten – für die Abwesenheit des linken oder des rechten Kindes steht.
Im unten stehenden Beispielcode wird angenommen, dass diese Richtung, die das letzte Ungleich-Ergebnis einer Suche nach dem Schlüssel von reflektiert, im Funktionsparameter dir ∈ {LEFT,RIGHT} übergeben wird.[Anm. 3]
Ferner wird angenommen, dass diese Suchfunktion den Stapel struct RBnode* Parents[] der Vorfahren von gebildet hat.[10] Der ebenfalls übergebene Zeiger struct RBnode** pParent zeigt in diesem Stapel auf den Zeiger des direkten Elters des einzufügenden Knotens. Wenn der Baum leer ist, ist pParent < &Parents[0] (und dir irrelevant).
Andernfalls ist Parents[0] gleich dem Zeiger auf den Wurzelknoten, pParent ≥ &Parents[0], und dir die Kindesrichtung des neuen Knotens.
Der Knoten wird zunächst rot gefärbt, damit die Schwarzhöhe des Baumes erhalten bleibt.[11]
Die darauf folgenden Aktionen überprüfen, ob die Rot-Schwarz-Balance im Baum eingehalten ist und stellen sie wenn erforderlich wieder her. Diese Reparatur wird als »Rebalancierung« (englisch rebalancing) bezeichnet.
Der neue Knoten (wie englisch node) ist der gerade betrachtete Problemknoten. Sein Elter ist (wie englisch parent). Der Großelter sei (wie englisch grandparent) und der Onkel (das Geschwister des Elters) (wie englisch uncle) genannt.
Der Kopf der Funktion RBinsert1 zum Einfügen eines Knotens nach einer vorher erfolgten und nicht erfolgreichen Suchoperation könnte wie folgt aussehen:[Anm. 4]
void RBinsert1(
RBtree* T, // -> Rot-Schwarz-Baum
struct RBnode* Parents[], // Liste der -> Vorfahren
struct RBnode** pParent, // ->-> Nachbarknoten (wird zum Elterknoten von N)
struct RBnode* N, // -> einzufügender Knoten
byte dir) // (Kindes-)Richtung der Einfügung ∈ {LEFT, RIGHT}
{
struct RBnode* P; // -> Elterknoten von N
struct RBnode* G; // -> Elterknoten von P
struct RBnode* U; // -> Onkel von N
assert(N != NIL); // N muss Zeiger zu einem echten Knoten sein.
N->left = NIL; // Dieses Programm ist hierfür zuständig.
N->right = NIL;
N->color = RED;
if (pParent >= &Parents[0]) { // N ist nicht die neue Wurzel
P = *pParent; // -> Nachbarknoten (wird zum Elterknoten von N)
assert(P->child[dir] == NIL); // darf kein echter Knoten sein
P->child[dir] = N; // neuer Knoten als dir-Kind von P
goto Start_E; // Sprung in die Schleife
} // end_if
// pParent < &Parents[0]
T->root = N; // N ist die neue Wurzel des Baums T.
return; // Einfügung fertiggestellt
do { // Beginn der (do while)-Schleife:
// pParent >= &Parents[0]
// ===> Es gibt den Elter P von N.
// (<=> Bedingung_E1 trifft NICHT zu.)
N = G; // neuer Problemknoten (kann die Wurzel sein)
P = *pParent; // -> Elterknoten von N
Start_E:
Rebalancierung nach dem Einfügen: Die Schleife zur Überprüfung und Reparatur des Baums steigt vom roten Blatt zur Wurzel auf. Ihre Invariante ist:
- Die Forderung !RR (»Nicht Rot-Rot«) gilt für alle Paare (Knoten←Elter) im Baum mit höchstens einer Ausnahme – beim Paar (←). Dies wird als »Rot-Verletzung« (englisch red violation) angesehen, welche als Problemknoten definiert.
Gilt !RR auch dort, entweder weil der Elter nicht existiert (Fall E1) oder schwarz ist (Fall E2), dann ist der Baum in Rot-Schwarz-Form. - Zu Beginn jedes Iterationsschritts ist der Problemknoten rot.
- Die Forderung S#= (»Schwarz-Zahl Gleich«) gilt für den ganzen Baum.
Einfügen: Zusammenschau der Fälle[Bearbeiten | Quelltext bearbeiten]
Die Zusammenschau bringt die Diagramme in einer auf die Farbkonstellation zugespitzten Form.
| »Bedingung« | Fall → |
»Rota- tion« |
»Neuzu- weisung« |
»Ergebnis« | → Test |
|||||||
| x | x | |||||||||||
| — | E1 | — | ✓ | |||||||||
| E2 | ✓ | |||||||||||
| E3 | := | ? | ? | ? | ? | E1 | 1 | |||||
| i | E4 | ↶ | := | o | E5 | 0 | ||||||
| o | E5 | ↷ | ✓ | |||||||||
| — | E6 | ✓ | ||||||||||
| Einfügen: Zusammenschau der Fälle[12] | ||||||||||||
Die möglichen Konstellationen lassen sich in sechs Fälle aufteilen, zu denen es Transformationen (enthaltend Rotation und/oder Umfärbung) gibt, die entweder auf der betrachteten Ebene oder über weitere Iterationsschritte auf höheren Ebenen zur Rebalancierung des Baumes führen.
In der nebenstehenden Tabelle wird ein Fall durch eine Zeile repräsentiert, die
- die »Bedingung«, das ist die Konstellation, die den Fall definiert und die dem Abschnitt »Bedingung« des zum Fall gehörigen Diagramms – falls vorhanden – entspricht,
- die Fallnummer,
- die Konstellation nach Umfärbung und/oder Rotation und ggf. Zuweisung in der Spaltengruppe »Ergebnis«
enthält. Eine Konstellation besteht aus maximal 4 Gegebenheiten, und zwar aus den Farben der 3 Knoten und Manche Fälle benötigen darüber hinaus eine vierte Angabe x zur Kindesrichtung von und zwar steht »o« (wie englisch outer) für eine Rechts-Rechts- oder Links-Links-Kindesrichtung von zu zu und »i« (wie englisch inner) für Rechts-Links oder Links-Rechts. Eine Zelle ist leer gelassen, wenn es auf die Angabe nicht ankommt. So gilt bspw. der Beispielcode im Fall E3 für beide Kindesrichtungen von und das, obwohl das zugehörige Diagramm nur eine Kindesrichtung zeigt.
Die Konstellationen in der Gruppe »Bedingung« genügen der Schleifeninvariante, und ihre logische Summe schöpft diese zu 100 % aus.
Die Transformation, deren Fallnummer in der Spalte Fall→ verlinkt ist, transformiert die Eingabe-Konstellation (als Teilbaum dargestellt im mit »Bedingung« beschrifteten Abschnitt des zum Fall gehörigen Diagramms) in die mit »Rotation« und/oder »Umfärbung« beschrifteten Abschnitte. Steht ein Häkchen »✓« in der Spalte →Test, dann reflektiert die Gruppe »Ergebnis« diesen Stand, mit dem alle Rot-Schwarz-Forderungen erfüllt sind und mit dem die Einfügeoperation abgeschlossen ist. Andernfalls steht dort die Fallnummer derjenigen Bedingung, auf die die transformierte und neu zugewiesene Konstellation zu testen ist, wobei die entsprechende Zuweisung, angegeben in der Spalte »Neuzuweisung« für den Problemknoten auch die Knoten sowie die Angabe x zur Kindesrichtung von neu zuordnet. Die Spaltengruppe »Ergebnis« und der mit »Neuzuweisung« beschriftete Abschnitt des Diagramms zeigt die Konstellation nach der Zuweisung; Fragezeichen stehen in den Zellen, auf deren Angabe es in den nachfolgenden Tests ankommt.
In der Spalte →Test kommt der Eintrag »E1« nur bei der Transformation_E3 vor. Er bedeutet einen neuen Iterationsschritt, der mit dem Test auf die while-Bedingung_E1 in der do while-Schleife beginnt, und zwar zwei Baumebenen (eine Schwarzebene ) näher an der Wurzel. Danach sind auch die Schwarzhöhen aller relevanten Teilbäume ≥ 1.
Da die Anzahl der Baumebenen mit der Höhe übereinstimmt, können maximal Iterationen vorkommen. Nun ist der Aufwand für eine Iteration beschränkt (d. h. in ) und damit der für die gesamte Einfügeoperation in (mit oder ohne Suchen). Die reine Rebalancierung ist gemäß Abschnitt Durchschnittliche und amortisierte Laufzeit im Mittel und amortisiert in
Bei einem Eintrag in der Spalte »Rotation« ist eine Rotation an der Transformation beteiligt. Man entnimmt der Tabelle sofort, dass bei einer Einfügeoperation maximal zwei Rotationen vorkommen, und zwar bei Fall E5 nach Fall E4. Denn nach einer Rotation kommt kein neuer Iterationsschritt – die Rotationen befinden sich endrekursiv am Ende der letzten ausgeführten Iteration.
Die Kindesrichtung von entscheidet insbesondere über die nachfolgenden Rotationsrichtungen. Bei Fall E4 bestimmt sie aber auch die Auswahl des Falles: Hat dieselbe Kindesrichtung wie dann ist die Angabe x (s. Zusammenschau) auf »o« für »außen«, sonst auf »i« für »innen« zu setzen.[13]
Im folgenden Beispielcode zur Operation Einfügen hält die Variable dir die Kindesrichtung des Knotens Die Diagramme zeigen immer als linkes Kind.
Jeder Fall wird unter seiner Fallnummer erläutert und einschließlich Test (auf die ihn charakterisierende »Bedingung«) und Transformation durch ein Stück C-Code genau beschrieben.[14]
Einfügen Fall E2[Bearbeiten | Quelltext bearbeiten]
Der Elter des (roten) Problemknotens ist schwarz.
Nach Eintritt dieser Bedingung gibt es kein Paar (Knoten←Elter) (mehr), das die Forderung !RR verletzt. Ferner ist nach Voraussetzung (Schleifeninvariante) die Anzahl der schwarzen Knoten auf allen Pfaden dieselbe. Damit ist der Baum ohne weitere Aktion in Rot-Schwarz-Form.
if (P->color == BLACK) // Bedingung_E2
// Transformation_E2:
return; // Einfügung fertiggestellt
// In den verbleibenden Fällen ist der Elter P rot.
if (pParent <= &Parents[0]) // Bedingung_E6
goto Fall_E6; // Der Elter P ist die Wurzel.
Im Folgenden ist der Elter nicht die Wurzel, so dass der Großelter existiert. Da rot ist, muss schwarz sein (so bei den folgenden Fällen E3, E4 und E5).
Einfügen Fall E3[Bearbeiten | Quelltext bearbeiten]
Sowohl der Onkel als auch der Elter des Problemknotens ist rot.
Die Umfärbung von und in schwarz und von in rot stellt die Forderung !RR im Teilbaum mit Wurzel wieder her (und zwar bei beiden Kindesrichtungen von ). Auf keinem Pfad ändert sich die Anzahl der schwarzen Knoten. Durch diese Transformation_E3 wird die »Rot-Verletzung« um zwei Baum-Ebenen (eine Schwarz-Ebene) nach oben verschoben mit als neuem Problemknoten.[Anm. 5]
G = *(--pParent); // Der Großelter G von N existiert.
dir = (P == G->right); // Kindesrichtung von P
U = G->child[1−dir]; // Onkel
if (U == NIL || U->color == BLACK)
goto Test_E4; // Der Onkel U ist schwarz.
// Bedingung_E3: N+P+U rot
// Transformation_E3:
// Umfärbung:
P->color = BLACK;
U->color = BLACK;
G->color = RED;
// Iteration zwei Ebenen (1 Schwarzebene) höher
} while (--pParent >= &Parents[0]);
// Ende der (do while)-Schleife
Einfügen Fall E1[Bearbeiten | Quelltext bearbeiten]
Der Problemknoten (hier: ) ist die Wurzel. Nach der obigen Transformation_E3 ist !RR (»Nicht Rot-Rot«) überall erfüllt, und der Baum in Rot-Schwarz-Form.
Allerdings könnte man eine rote Wurzel ohne Verletzung der Rot-Schwarz-Forderungen immer auf schwarz umfärben[7] – was z. B. den Test auf Bedingung_E6 und den Fall E6 überflüssig machen würde.
// Bedingung_E1: pParent < &Parents[0]
// ===> G ist die alte und neue Wurzel des Baums T.
return; // Einfügung fertiggestellt
Einfügen Fall E4[Bearbeiten | Quelltext bearbeiten]
Der Problemknoten hat keinen oder einen schwarzen Onkel und hat eine Kindesrichtung entgegengesetzt zu der seines roten Elters d. h., ist innerer Enkel.
Eine Rotation um [Anm. 6] vertauscht die Rollen von und und zwar eine Linksrotation, wenn linkes Kind (d. h. dir == LEFT) ist, sonst eine Rechtsrotation.
(Im Folgenden wird eine solche Rotation als dir-Rotation bezeichnet.)
Dadurch werden die Pfade des Teilbaums so verändert, dass sie durch einen Knoten mehr und die des Teilbaums durch einen weniger führen. Da jedoch in beiden Fällen rote Knoten den Unterschied ausmachen, ändert sich an der Anzahl der schwarzen Knoten nichts, womit die Forderung S#= und die Schleifeninvariante erfüllt bleibt.
Die Ergebniskonstellation entspricht der Eingangskonstellation des Falles E5 mit als dem neuen Problemknoten.
Test_E4:
if (N != P->child[dir]) {
// Bedingung_E4: N ist innerer Enkel
// && N+P rot && U schwarz
// Transformation_E4:
// dir-Rotation um P:
P->child[1−dir] = N->child[dir]; // NIL oder neuer Zeiger zu Teilbaum 3
N->child[dir] = P;
G->child[dir] = N;
// Zuweisung nach der Transformation:
N = P; // neuer Problemknoten (rot) und äußerer Enkel
P = G->child[dir]; // neuer Elter von N (rot)
}
Einfügen Fall E5[Bearbeiten | Quelltext bearbeiten]
Der Problemknoten hat keinen oder einen schwarzen Onkel. Seine Kindesrichtung ist dieselbe wie die von d. h., ist äußerer Enkel.
Eine (nicht-dir)-Rotation[Anm. 7] um [Anm. 6] macht zum Elter sowohl von als auch von Da rot war, muss wegen Forderung !RR schwarz sein. Invertiert man nun die Farben von und so ist in dem dadurch entstehenden Baum die Forderung !RR wieder erfüllt. Die Forderung S#= bleibt ebenfalls erfüllt, da alle Pfade, die durch einen dieser drei Knoten laufen, vorher durch liefen und nun alle durch laufen, der inzwischen – wie vor der Transformation – der einzige schwarze der drei Knoten ist.
// Bedingung_E5: N ist äußerer Enkel && N+P rot && U schwarz
// Transformation_E5:
// (nicht-dir)-Rotation um G:
G->child[dir] = P->child[1−dir]; // NIL oder neuer Zeiger zu Teilbaum 3
P->child[1−dir] = G;
if (--pParent >= &Parents[0]) {
// Ersetze G bei seinem Elter durch P:
U = *pParent;
U->child[G == U->right] = P;
}
else // G war die Wurzel
T->root = P; // P ist die neue Wurzel
// Umfärbung:
P->color = BLACK;
G->color = RED;
return; // Einfügung fertiggestellt
Einfügen Fall E6[Bearbeiten | Quelltext bearbeiten]
Der rote Elter des Problemknotens ist gleichzeitig die Wurzel des Baums.
Eine Umfärbung von in schwarz stellt die Forderung !RR im ganzen Baum wieder her. Auf jedem Pfad erhöht sich die Anzahl der schwarzen Knoten um 1.
Fall_E6:
// Der Elter P von N ist die Wurzel des Baums.
// Transformation_E6:
// Umfärbung:
P->color = BLACK;
// Da P rot war,
// erhöht sich die Schwarzhöhe des Baumes um 1.
return; // Einfügung fertiggestellt
} // Ende RBinsert1
Operation Löschen[Bearbeiten | Quelltext bearbeiten]
Das Löschen eines Knotens, sein Name sei , aus einem Rot-Schwarz-Baum erfolgt wie bei einem binären Suchbaum.
Hat der Knoten ein oder kein Kind, dann kann die folgende Überlegung übersprungen werden.
- Hat aber zwei (echte) Kinder, dann nimmt man, ohne letztlich die Sortierreihenfolge zu stören, als effektiv zu löschenden Knoten seinen hinsichtlich Sortierreihenfolge rechten (resp. linken) Nachbarknoten, welcher kein linkes (resp. kein rechtes) Kind haben kann.[15] Ein solcher Nachbarknoten ist ein Blatt oder Halbblatt, das tiefster linker Nachkomme des rechten Kindes (resp. tiefster rechter Nachkomme des linken Kindes) von ist.[Anm. 8]
Geht man so vor, dann kann man sich darauf beschränken, dass das initiale maximal ein Kind hat.
Mit (wie englisch parent) sei der Elter von und mit dir (wie englisch direction) die Kindesrichtung von (rechtes oder linkes Kind von ) bezeichnet.
Einfache Fälle[Bearbeiten | Quelltext bearbeiten]
Den Fall, dass die kinderlose Wurzel ist, erledigt man sofort, indem man diese durch einen NIL-Knoten ersetzt.
Hat genau ein Kind, so ist dieses zwangsläufig rot.
Man färbt es schwarz und macht es an der Kindesrichtung dir zum Kind von Damit ist aus dem Baum entfernt, und die Forderung !RR (»Nicht Rot-Rot«) bleibt erfüllt. Ferner verlaufen nun alle Pfade, die durch den gelöschten schwarzen Knoten verliefen, durch sein nunmehr schwarzes Kind, so dass auch die Forderung S#= (»Schwarz-Zahl Gleich«) erfüllt bleibt.
Hat kein Kind und ist rot, so wird es bei seinem (schwarzen) Elter einfach durch einen NIL-Knoten ersetzt. Und da alle Pfade, die durch den roten Knoten verliefen, nach seiner Entfernung aus dem Baum durch einen roten Knoten weniger verlaufen, ändert sich an der Anzahl der schwarzen Knoten nichts, womit die Forderung S#= erfüllt bleibt.
Das Löschen eines schwarzen Blattes[Bearbeiten | Quelltext bearbeiten]
Komplizierter sind die Fälle, wo nicht die Wurzel ist, kein Kind hat und schwarz, also ein schwarzes Blatt ist.
Als solches hat ein (echtes) Geschwister, das (nicht-dir)-Kind[Anm. 7] von welches mit (wie englisch sibling) bezeichnet sei.
Dessen (möglicherweise leeres) dir-Kind (wie englisch close) ist der »nahe« Neffe von mit derselben Kindesrichtung; das andere (ebenfalls möglicherweise leere) Kind (wie englisch distant) der »ferne« Neffe.
Nach der Ersetzung von bei durch NIL sei diese Stelle im Baum weiterhin durch bezeichnet. Die durch führenden Pfade enthalten einen schwarzen Knoten weniger als vorher, also einen weniger als die ebenfalls durch führenden Pfade durch das Geschwister . Somit ergibt sich bei eine Verletzung der Forderung S#=, eine so genannte »Schwarz-Verletzung« (englisch black violation). Der Knoten wird deshalb als Problemknoten aufgefasst.
Im nachfolgenden Beispielcode ist angenommen, dass eine vorausgehende Suchfunktion, die den zu löschenden Knoten lokalisiert hat, den Stapel struct RBnode* Parents[] von dessen Vorfahren gebildet[10] und dessen Zeiger an die Löschfunktion übergeben hat.
Ist die Wurzel, dann zeigt der ebenfalls übergebene Zeiger struct RBnode** pParent vor diesen Stapel (pParent < &Parents[0]).
Andernfalls zeigt er in diesem Stapel auf den Zeiger zum direkten Elter des zu löschenden Knotens, und es ist pParent ≥ &Parents[0] sowie Parents[0] gleich dem Zeiger auf den Wurzelknoten.
Eine andere, häufig verwendete Art, den Aufstieg im Baum zu unterstützen, ist die Implementierung eines Elterzeigers pro Knoten.
Der Kopf einer Funktion RBdelete2 zum Löschen eines schwarzen Knotens ohne Kind, der nicht die Wurzel ist, könnte dann wie folgt aussehen:[Anm. 9]
void RBdelete2(
RBtree* T, // -> Rot-Schwarz-Baum
struct RBnode* Parents[], // Liste der -> Vorfahren
struct RBnode** pParent, // ->-> Elterknoten von N
struct RBnode* N) // -> zu löschender Knoten, hier: schwarz
{
byte dir; // Richtung ∈ {LEFT, RIGHT}
struct RBnode* P; // -> Elterknoten von N
struct RBnode* S; // -> Geschwisterknoten von N
struct RBnode* C; // -> naher Neffe
struct RBnode* D; // -> ferner Neffe
// Für RBdelete2 muss erfüllt sein:
assert(N != NIL);
assert(pParent >= Parents[0]); // N ist nicht die Wurzel.
P = *pParent; // Elter von N
dir = (N == P->right); // Kindesrichtung von N:
// Wenn nicht right, dann left:
assert(N != P->right ? N == P->left : true);
assert(N->color == BLACK);
assert(N->left == NIL);
assert(N->right == NIL);
// Ersetze N bei seinem Elter P durch NIL:
P->child[dir] = NIL;
goto Start_L; // Sprung in die Schleife
Rebalancierung nach dem Löschen: Die Schleife zur Überprüfung und Reparatur des Baums steigt vom Problemknoten d. i. zunächst das neue Pfadende N = NIL, zur Wurzel auf. Ihre Invariante ist:
- Die Anzahl der schwarzen Knoten in den Pfaden durch ist um eins kleiner als vorher, wogegen sie in den anderen Pfaden ungeändert ist. (Dies kann durch Abzählen der schwarzen Kreisflächen in der mit »Bedingung« beschrifteten Ausgangskonstellation eines Diagramms nachvollzogen werden.) Das bedeutet, dass, wenn es andere Pfade gibt, beim Elter von eine »Schwarz-Verletzung« vorliegt.
- hat die Schwarzhöhe und ist in der ersten Iterationsstufe leer (sein Zeigerwert NIL). Dieses Pfadende wird in den Diagrammen der ersten Iterationsstufe durch einen blauen Pfeil nach links
 symbolisiert.
symbolisiert.
In den höheren Iterationsstufen ist ein echter schwarzer Knoten und wird in den Diagrammen mit der blauen Kontur des Problemknotens gebracht.[Anm. 10] - Die Forderung !RR (»Nicht Rot-Rot«) ist überall erfüllt.
Die Zusammenschau bringt die Diagramme in einer auf die Farbkonstellation zugespitzten Form.
| »Bedingung« | Fall → |
»Rota- tion« |
»Neuzu- weisung« |
»Ergebnis« | → Test |
|||||||
| — | L1 | — | ✓ | |||||||||
| L2 | := | ? | ? | ? | ? | L1 | 1 | |||||
| L3 | ↶ | := | L6 | 0 | ||||||||
| L5 | 0 | |||||||||||
| L4 | 0 | |||||||||||
| L4 | ✓ | |||||||||||
| L5 | ↷ | := | L6 | 0 | ||||||||
| L6 | ↶ | ✓ | ||||||||||
| Löschen: Zusammenschau der Fälle[16][17] | ||||||||||||
Löschen: Zusammenschau der Fälle[Bearbeiten | Quelltext bearbeiten]
Die möglichen Farbkonstellationen lassen sich in sechs Fälle gruppieren, zu denen es Transformationen (enthaltend Rotation und/oder Umfärbung) gibt, die entweder auf der betrachteten Ebene oder über weitere Iterationsschritte auf höheren Ebenen zu einer Rebalancierung des Baumes führen.
In der nebenstehenden Tabelle wird ein Fall durch eine Zeile repräsentiert, die
- die »Bedingung«, das ist die Konstellation, die den Fall definiert,
- die Fallnummer,
- die Konstellation nach Transformation und ggf. Zuweisung in der Spaltengruppe »Ergebnis«
enthält. Eine Konstellation (4 Spalten) besteht aus den Farben der 4 Knoten
Eine Zelle ist leer gelassen, wenn es auf die Angabe nicht ankommt. Zweimal ![]() auf einer Zeile bedeutet zweimal dieselbe Knotenfarbe, schwarz oder rot.
auf einer Zeile bedeutet zweimal dieselbe Knotenfarbe, schwarz oder rot.
Die Konstellationen in der Gruppe »Bedingung« genügen der Schleifeninvariante, und ihre logische Summe schöpft diese zu 100 % aus. Sie sind im mit »Bedingung« beschrifteten, dem obersten Abschnitt des zum Fall gehörenden Diagramms nochmals als Teilbaum skizziert.
Die Transformation, deren Fallnummer in der Spalte Fall→ verlinkt ist, transformiert die Eingabe in Konstellationen, die in den mit »Rotation« und/oder »Umfärbung« beschrifteten Abschnitten des Diagramms des Falles dargestellt sind. Steht ein Häkchen »✓« in der Spalte →Test, dann reflektiert die Gruppe »Ergebnis« den Endstand, und die Löschoperation ist durch die Transformation abgeschlossen. Andernfalls steht dort die Fallnummer derjenigen Bedingung, auf die die transformierte und neu zugewiesene Konstellation zu testen ist, wobei die entsprechende Zuweisung, angegeben in der Spalte »Neuzuweisung« für den Problemknoten auch die Knoten eindeutig bestimmt. Die Spaltengruppe »Ergebnis« und der mit »Neuzuweisung« beschriftete Abschnitt des Diagramms zeigt die Konstellation nach der Zuweisung; Fragezeichen stehen bei den Knoten, auf deren Farbe es in den nachfolgenden Tests ankommt.
Der Eintrag »L1« kommt nur bei der Transformation_L2 vor und bedeutet einen neuen Iterationsschritt auf der um 1 höheren Ebene im Baum (gleichzeitig eine Schwarzebene ), beginnend mit dem Test auf die Bedingung_L1. Danach sind die Schwarzhöhen aller Teilbäume ≥ 1. Die Anzahl der Ebenen stimmt mit der Höhe überein, so dass höchstens Iterationen vorkommen können. Nun ist der Aufwand für eine Iteration beschränkt (d. h. in ) und damit der für die gesamte Löschoperation in Gemäß Abschnitt Durchschnittliche und amortisierte Laufzeit ist der Rebalancierungsaufwand im Mittel sogar konstant.
Bei einem Eintrag in der Spalte Rotation ist eine Rotation an der Transformation beteiligt. Und die Tabelle zeigt, dass bei einer Löschung maximal drei Rotationen (von Fall L3 über L5 zu L6) erforderlich sind. Denn nach einer Rotation kommt kein neuer Iterationsschritt – die Rotationen befinden sich endrekursiv am Ende der letzten Iteration.
Die Kindesrichtung des Problemknotens bestimmt sowohl die nachfolgenden Rotationsrichtungen wie die Kindesrichtungen der Neffen und Im Beispielcode wird dies mithilfe der Variablen dir gelöst.[13]
Die Diagramme bei den Fällen zeigen jedoch immer links von .
// Beginn der (do while)-Schleife:
do {
// pParent >= &Parents[0]
// ===> Bedingung_L1 trifft NICHT zu
N = P; // neuer Problemknoten (kann die Wurzel sein)
P = *pParent;
dir = (N == P->right); // Kindesrichtung von N
Start_L:
S = P->child[1−dir]; // Geschwister von N
if (S->color == RED)
goto Fall_L3; // Bedingung_L3: S rot ===> P+C+D schwarz
// S ist schwarz:
D = S->child[1−dir]; // ferner Neffe
if (D != NIL && D->color == RED)
goto Fall_L6; // der ferne Neffe D ist rot
C = S->child[ dir]; // naher Neffe
if (C != NIL && C->color == RED)
goto Fall_L5; // der nahe Neffe C ist rot
// Beide Neffen sind == NIL (erste Iteration) oder schwarz (später).
if (P->color == RED)
goto Fall_L4; // P rot && C+S+D schwarz <==> Bedingung_L4
Jeder Fall wird unter seiner Fallnummer erläutert und einschließlich Test (auf die ihn charakterisierende Bedingung) und Transformation durch ein Stück C-Code genau beschrieben.[14][Anm. 5]
Löschen Fall L2[Bearbeiten | Quelltext bearbeiten]
Der Elter des Problemknotens und das Geschwister sind schwarz, ebenso die Kinder und von falls sie existieren.
Die Umfärbung des Knotens von schwarz in rot vermindert in allen Pfaden, die durch führen, die Zahl der schwarzen Knoten um 1 auf . Das betrifft genau die Pfade, die durch aber nicht durch führen, welch letztere Pfade vorher schon genau schwarze Knoten enthalten haben. Damit sind es schwarze Knoten in den Pfaden, die durch führen, und in denen, die nicht durch führen – wenn es denn solche noch gibt. Somit wird die erste Bedingung der Schleifeninvariante mit nunmehr als Problemknoten erfüllt.
// Bedingung_L2: P+C+S+D schwarz
// Transformation_L2:
// Umfärbung:
S->color = RED;
// Fortsetzung der Überprüfung des Baums
// eine Ebene höher durch Testen auf die
// Bedingung_L1:
} while (--pParent >= &Parents[0]);
// Ende der (do while)-Schleife.
Löschen Fall L1[Bearbeiten | Quelltext bearbeiten]
Der Problemknoten (hier: ) ist die Wurzel.
In diesem Fall ist man fertig, da überhaupt alle Pfade durch führen (und somit alle Pfade einen schwarzen Knoten weniger enthalten als vorher). Die Schwarzhöhe des Baumes verringert sich dabei um 1.
// Bedingung_L1: pParent < &Parents[0]
// ===> P ist die alte und neue Wurzel des Baums T.
return; // Löschung fertiggestellt
Löschen Fall L3[Bearbeiten | Quelltext bearbeiten]
Das Geschwister des Problemknotens ist rot.
Eine Rotation um [Anm. 11] macht zum Großelter von und zwar eine Linksrotation, wenn linkes Kind (d. h. dir == LEFT) ist, sonst eine Rechtsrotation.
(Im Folgenden wird eine solche Rotation als dir-Rotation bezeichnet.)
Danach invertiert man die Farben von und Alle Pfade haben weiterhin dieselbe Anzahl an schwarzen Knoten, aber hat nun ein schwarzes Geschwister, und einen roten Elter, weswegen man nun zu Fall L4, L5 oder L6 weitergehen kann – mit als altem und neuem Problemknoten.[Anm. 5]
Fall_L3:
// Bedingung_L3: S rot && P+C+D schwarz
// Transformation_L3:
C = S->child[dir]; // aufbewahren
// dir-Rotation um P:
P->child[1−dir] = C; // neuer Elter von C
S->child[dir] = P;
if (--pParent >= &Parents[0]) {
// Ersetze P bei seinem Elter durch S:
D = *pParent;
D->child[P == D->right] = S;
}
else // P war die Wurzel
T->root = S; // S ist die neue Wurzel
// Umfärbung:
S->color = BLACK;
P->color = RED;
// Zuweisung nach der Transformation:
S = C; // neues Geschwister von N (schwarz)
D = S->child[1−dir]; // ferner Neffe
if (D != NIL && D->color == RED)
goto Fall_L6; // der ferne Neffe D ist rot
C = S->child[ dir]; // naher Neffe
if (C != NIL && C->color == RED)
goto Fall_L5; // der nahe Neffe C ist rot
// Beide Neffen sind == NIL (erste Iteration)
// oder schwarz (später).
// Also P rot && C+S+D schwarz <==> Bedingung_L4.
// Das ist Fall_L4:
Löschen Fall L4[Bearbeiten | Quelltext bearbeiten]
Der Elter von ist rot, aber sowohl das Geschwister des Problemknotens als auch dessen Kinder und sind schwarz, falls sie existieren.
Eine Invertierung der Farben von und lässt die Anzahl der schwarzen Knoten auf den Pfaden, die durch laufen, unverändert, fügt aber auf allen Pfaden durch einen schwarzen Knoten hinzu und gleicht damit den fehlenden schwarzen Knoten auf diesen Pfaden aus.
Fall_L4:
// Bedingung_L4: P rot && C+S+D schwarz
// Transformation_L4:
// Umfärbung:
S->color = RED;
P->color = BLACK;
return; // Löschung fertiggestellt
Löschen Fall L5[Bearbeiten | Quelltext bearbeiten]
Das Geschwister von ist schwarz, der nahe Neffe rot, während der ferne Neffe falls er existiert, schwarz ist. Der im Diagramm rot-schwarz dargestellte Knoten behält seine Farbe, rot oder schwarz.
Eine (nicht-dir)-Rotation um [Anm. 6] macht zum Elter von und zugleich zum Geschwister von Danach invertiert man die Farben von und
Dadurch werden die Pfade des Teilbaums so verändert, dass sie durch einen roten Knoten weniger und die Pfade durch den Knoten durch einen mehr führen. Die Zahl der schwarzen Knoten auf diesen Pfaden bleibt jedoch gleich.
Ferner hat nun ein schwarzes Geschwister, dessen fernes Kind, rot ist, womit man zum Fall L6 weitergehen kann. Weder noch noch die Schwarzhöhe werden durch diese Transformation beeinflusst.
Fall_L5:
// Bedingung_L5: S+D schwarz && C rot
// Transformation_L5:
// (nicht-dir)-Rotation um S:
S->child[dir] = C->child[1−dir]; // NIL oder neuer Zeiger zu Teilbaum 3
C->child[1−dir] = S;
// dadurch wird S zum fernen Neffen von N
P->child[1−dir] = C;
// Umfärbung:
C->color = BLACK;
S->color = RED;
// Zuweisung nach der Transformation:
D = S; // neuer ferner Neffe
S = C; // neues Geschwister von N
// Weiter zu Fall_L6:
Löschen Fall L6[Bearbeiten | Quelltext bearbeiten]
Die Farbe des Elters ist beliebig. Das Geschwister von ist schwarz, und der ferne Neffe von ist rot.
Eine dir-Rotation um [Anm. 6] macht zum Großelter von
Nun reicht es, die Farbe von zu geben und sowie schwarz zu färben. hat immer noch dieselbe Farbe, wodurch die Forderung !RR erfüllt bleibt. Aber hat nun einen zusätzlichen schwarzen Vorfahren: Falls vor der Transformation noch nicht schwarz war, so ist er nach der Transformation schwarz, und falls schon schwarz war, so hat nun als schwarzen Großelter, weswegen die Pfade, die durch führen, nun einen zusätzlichen schwarzen Knoten passieren.
Bei den Pfaden, die sich ändern und die nicht durch führen, gibt es zwei Möglichkeiten:
- Der Pfad führt durch die beliebig eingefärbte Wurzel des Teilbaums , die das neue Geschwister von ist. Dann muss der Pfad sowohl vor als auch nach der Transformation durch und führen. Da die beiden Knoten aber nur ihre Farben vertauscht haben, ändert sich an der Anzahl der schwarzen Knoten auf dem Pfad nichts.
- Der Pfad führt durch den neuen Onkel von welcher das (nicht-
dir)-Kind des Geschwisters ist. In diesem Fall führte der Pfad vorher durch und . Nach der Transformation führt er aber nur noch durch der von Rot auf Schwarz (die vorige Farbe von ) umgefärbt wurde, und den Knoten welcher die Farbe von angenommen hat. Somit ändert sich die Anzahl der schwarzen Knoten eines solchen Pfades nicht.
Da die Anzahl der schwarzen Knoten in den Pfaden, die durch führen, sich um 1 erhöht, und in denen, die nicht durch führen, sich nicht ändert, ist die Forderung S#= wiederhergestellt.
Fall_L6:
// Bedingung_L6: S schwarz && D rot
// Transformation_L6:
// dir-Rotation um P:
P->child[1−dir] = S->child[dir]; // NIL oder neuer Zeiger zu Teilbaum 3
S->child[dir] = P;
if (--pParent >= &Parents[0]) // P war nicht die Wurzel
{
// Ersetze P bei seinem Elter durch S:
N = *pParent;
N->child[P == N->right] = S;
}
else
T->root = S; // S ist die neue Wurzel
// Umfärbung:
S->color = P->color;
P->color = BLACK;
D->color = BLACK;
return; // Löschung fertiggestellt
} // Ende RBdelete2
Operationen mit ganzen Rot-Schwarz-Bäumen[Bearbeiten | Quelltext bearbeiten]
Die folgenden zwei Operationen haben ganze Rot-Schwarz-Bäume als Ein- und Ausgabeoperanden. Sie gehören nicht zum Standardsatz und fehlen in manchen Implementierungen. Es soll aber hier gezeigt werden, dass auch sie mit logarithmischem Aufwand durchgeführt werden können.
Verketten (Join)[Bearbeiten | Quelltext bearbeiten]

Die Operation JOIN(TL,k,TR) verkettet (konkateniert) (englisch: join oder concat) zwei Rot-Schwarz-Bäume über einen Einzelschlüssel mit logarithmischem Aufwand.[18] Für die Sortierfolge müssen natürlich alle Schlüssel des ersten Baums TL dem Einzelschlüssel k und dieser allen Schlüsseln des zweiten TR vorangehen.[19]
Die In-Order-Traversierung des verketteten Baums entspricht der Nacheinanderausführung der Traversierung des ersten Baums, gefolgt von der des einzelnen Knotens, gefolgt von der des zweiten Baums.
Skizze des Algorithmus:
Ohne Beschränkung der Allgemeinheit sei der erste Baum nicht niedriger als der zweite, und der zweite habe eine schwarze Wurzel (Knoten in der Abbildung) der Schwarzhöhe . Ferner sei dem zweiten Baum sein erstes Element bereits entnommen. Es spielt nachher die Rolle eines „Bindeglieds“.
Man steigt an der rechten Flanke des ersten Baums bis zu einem schwarzen Knoten der Schwarzhöhe hinunter, sein Name sei .
Der Knoten wird rot gefärbt und zum rechten Kind des Elters von gemacht.
Ist schwarz, dann ist der verkettete Baum in Rot-Schwarz-Form und die Verkettung abgeschlossen.
Ist jedoch rot, dann ist sein linkes Kind schwarz.
Nun lässt sich eine Reparaturschleife anschließen, die zur Wurzel aufsteigend dieselbe Schleifeninvariante hat wie die Operation Einfügen,
und ist der Problemknoten der ersten Iterationsstufe.
Massenoperationen[Bearbeiten | Quelltext bearbeiten]
Aufbauend auf der JOIN-Operation können weitere Massen- und Mengenoperationen gebildet werden,[20] die allesamt logarithmische Laufzeit haben, so z. B. die komplementäre Operation des Aufspaltens (englisch: split) eines Baums an einem Pfad.
Die Massenlöschung von allen Schlüsseln in einem zusammenhängenden Bereich (Intervall) kann durch zweimaliges Spalten und einmaliges Verketten geschehen oder, wenn das kleinste oder größte Element mit dabei ist, durch einmaliges Spalten. In ähnlicher Weise lässt sich ein Intervall mit logarithmischem Aufwand als Rot-Schwarz-Baum aus einem Rot-Schwarz-Baum herauspräparieren.
Eine Masseneinfügung kann durch einmaliges Spalten und zweimaliges Verketten durchgeführt werden, sofern die Menge als Rot-Schwarz-Baum vorbereitet ist und ihre Schlüssel in einem Intervall liegen, das im Zielbaum nicht vorkommt.
Mengenoperationen[Bearbeiten | Quelltext bearbeiten]
Im selben Aufsatz wurde gezeigt, dass auch die Mengenoperationen Durchschnitt, Vereinigung und Differenz von digital repräsentierten (endlichen) Mengen sehr effizient (in logarithmischer Zeit) und in „natürlicher“ Parallelität implementiert werden können (s. Binärer Suchbaum#Effiziente Massen- und Mengenoperationen aufbauend auf der JOIN-Operation). Blelloch et. al. zeigen, dass sich diese Algorithmen sich so auf die 4 balancierten Suchbäume (AVL-, Rot-Schwarz-, Splay- und BB[α]) übertragen lassen, dass sich alles Spezifische im JOIN-Algorithmus abspielt.
Höhenbeweis[Bearbeiten | Quelltext bearbeiten]
Wie schon in der Einleitung ausgeführt, ist die besondere Eigenschaft von Rot-Schwarz-Bäumen, dass sie in logarithmischer Zeit – genauer in mit als der Anzahl der Schlüssel – ein Element im Baum suchen, löschen oder einfügen können. Diese Operationen sind auf allen binären Suchbäumen von der Höhe des Baumes abhängig. Je niedriger die Höhe des Baumes ist, desto schneller laufen die Operationen. Kann man nun beweisen, dass ein binärer Suchbaum mit Elementen nie eine gewisse Höhe (im Falle des Rot-Schwarz-Baumes ) überschreitet, so hat man bewiesen, dass die oben genannten Operationen im schlechtesten Fall logarithmische Kosten haben.
Rot-Schwarz-Bäume mit kleinster Knotenzahl zu gegebener Höhe

jeweils mit minimaler Knotenzahl 1,2,4,6 resp. 10.
Zu gibt es einen Rot-Schwarz-Baum der Höhe mit
(mit Gauß-Klammern ) wenn gerade wenn ungerade
Knoten, und keinen mit weniger.[Anm. 12][Anm. 13]
Beweis
Damit ein Rot-Schwarz-Baum einer bestimmten Höhe eine minimale Knotenzahl besitzt, muss er genau einen längsten Pfad enthalten, und dieser eine größtmögliche Anzahl roter Knoten, um eine möglichst große Baumhöhe mit möglichst kleiner Schwarzhöhe zu erreichen. Seine Einfärbung hat also unten beim Blatt mit Rot zu beginnen, und sich in der Folge nach oben bis zur Wurzel mit Schwarz und Rot streng abwechselnd fortzusetzen. Außerhalb dieses die Baumhöhe definierenden Pfades hat er nur schwarze Knoten.[21] Denn angenommen, es gäbe dort einen roten Knoten, dann beeinträchtigt das Entfernen desselben die Rot-Schwarz-Eigenschaften nicht, sofern einer von seinen zwei (schwarzen) Kindknoten an seine Stelle nachrückt und der andere gleichzeitig einschließlich seines Teilbaums entfernt wird. Alle Teilbäume außerhalb des längsten Pfades sind somit vollständige Binärbäume mit ausschließlich schwarzen Knoten.
Es gibt genau einen Rot-Schwarz-Baum der Höhe mit einem roten Blatt, welches gleichzeitig die Wurzel ist. Also ist in Übereinstimmung mit
Bei einem Minimalbaum (RBh in der Abbildung) der Höhe sind die zwei Kindbäume der Wurzel von unterschiedlicher Höhe: der höhere enthält den die Höhe definierenden längsten Pfad und ist ein Minimalbaum der Höhe mit Knoten und der Schwarzhöhe ; der niedrigere ist ein vollständiger Binärbaum mit Höhe = Schwarzhöhe hat also Knoten. Damit ist rekursiv
| (großer Kindbaum) | (Wurzel) | (kleiner Kindbaum) | ||||||
| woraus man | ||||||||
ausrechnet. ■
Der Graph der Funktion ist konvex nach unten und stückweise linear mit den Ecken an den Punkten mit Ferner ist A027383(h–1) für mit der Folge A027383 in OEIS.
- Umformung
Wegen (eine Folge von ) haben wir für ungerades die Ungleichung
so dass sich für alle (geraden wie ungeraden)
ergibt. Da die kleinste Knotenzahl für alle Rot-Schwarz-Bäume der Höhe ist, gilt
so dass sich im Intervall
| (vollständiger Binärbaum) | (minimaler RB-Baum) |
- Folgerung
Somit folgt die Behauptung, dass ein Rot-Schwarz-Baum eine maximale Höhe von hat und damit die Operationen suchen, einfügen und löschen in logarithmischer Zeit erledigen kann. Drückt man dieses Ergebnis in der O-Notation aus, so ergibt sich für die Kosten der oben genannten Operationen, dass sie alle in liegen mit als der Zahl der Schlüssel.[Anm. 15]
Durchschnittliche und amortisierte Laufzeit[Bearbeiten | Quelltext bearbeiten]
Der Rot-Schwarz-Baum bietet amortisiert konstante Rebalancierungskosten[23] und damit auch im Mittel konstante.
Anwendungen von (binären) Suchbäumen, die neben Sequenzen von Einfügungen und Löschungen auch Suchoperationen enthalten, sind asymptotisch durch die logarithmische Laufzeit der letzteren dominiert. Interessant ist der amortisiert konstante Modifikations-Aufwand jedoch, wenn der Suchbaum persistent gehalten werden soll, d. h. alle Versionen zugänglich bleiben sollen (s. a. Persistent data structure).[8][24]
Anzahlen von Rot-Schwarz-Bäumen[Bearbeiten | Quelltext bearbeiten]
Die Folge A001131 in OEIS gibt in Abhängigkeit von der Knotenzahl die Gesamtzahl der Rot-Schwarz-Bäume, Folge A001137 in OEIS derer mit schwarzer Wurzel und Folge A001138 in OEIS derer mit roter Wurzel.

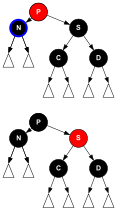
Die nebenstehende Abbildung zeigt den balancierten Binärbaum mit 3 Schlüsseln in 3 verschiedenen regelkonformen Rot-Schwarz-Einfärbungen. Beim Suchen und Traversieren ist wegen der identischen Verzweigungen der 3 Bäume alles Verhalten einschließlich Laufzeit gleich. Unterschiede gibt es aber bei Modifikationen, bspw. bei Einfügungen: Bei der linken Einfärbung sind alle Einfügungen vom Typ Transformation_E3 gefolgt von Transformation_E1, bei den rechten 2 Einfärbungen sind alle vom Typ Transformation_E2.
Zwar wird in einem reinen Einfügeszenario von den 3 möglichen Bäumen mit 3 Knoten (Schlüsseln) nur der eine Baum mit schwarzer Wurzel und 2 roten Kindern (der linke in der Abbildung) gebildet. Bezieht man jedoch Löschungen mit ein, dann kommen die zwei anderen Rot-Schwarz-Bäume (rechts in der Abbildung) hinzu,

und zwar der mit roter Wurzel über
und der mit schwarzer Wurzel über
- 6 Einfügungen und 3 Löschungen
und dies mit den oben beschriebenen Algorithmen für Einfügung und Löschung – jeweils bei geeignet gewählter Schlüsselfolge, die durch den Knoten mit blauer Kontur angegeben ist.
Verwandtschaft mit 2-3-4-Bäumen[Bearbeiten | Quelltext bearbeiten]




Die 4 kleinen Grafiken links und rechts zeigen, wie kleine Bausteine eines Rot-Schwarz-Baums (linke Hälften der Grafiken) mit einem (dicken) Knoten eines 2-3-4-Baums (rechte Hälften der Grafiken) zur Entsprechung gebracht werden können. Man erzeugt aus einem Rot-Schwarz-Baum einen 2-3-4-Baum, indem man rote Kinder entsprechend ihrer Kindesrichtung links oder rechts als Datenelemente in den schwarzen Elterknoten hereinholt.[25][26]

Umgekehrt kann man einen 2-3-4-Baum ganz einfach in einen Rot-Schwarz-Baum überführen: Aus einem Knoten mit 2 Datenelementen und 3 Kindzeigern (wie der Knoten [NIL,1,6] in der Abbildung) wird ein schwarzer Knoten (Datenelement) mit 1 Kindzeiger und einem roten Kindknoten (Datenelement), der noch 2 Kindzeiger enthält; aus einem Knoten mit 3 Datenelementen und 4 Kindzeigern (wie die Knoten [8,13,17] und [22,25,27] in der Abbildung) wird ein schwarzer Knoten (Datenelement) mit 2 roten Kindknoten (jeweils 1 Datenelement und 2 Kindzeiger).
Darüber hinaus gibt es Entsprechungen bei den Modifikationsoperationen (Einfügen, Löschen) zwischen Farbwechsel und Rotationen auf Seite der Rot-Schwarz-Bäume und den Aktionen Spalten (englisch split) und Verschmelzen (englisch fuse) bei den 2-3-4-Bäumen.
Im Gegensatz zu 2-3-4-Bäumen muss man bei Rot-Schwarz-Bäumen nicht den »Füllzustand« (Speicherausnutzung, englisch fill factor) der Knoten beobachten und verwalten, weshalb letztere als sehr effiziente Art der Implementierung der 2-3-4-Bäume gelten.[27]
Vergleich mit AVL-Baum[Bearbeiten | Quelltext bearbeiten]
Die Menge der AVL-Bäume ist eine echte Teilmenge in der Menge der Rot-Schwarz-Bäume. Denn jeder Binärbaum, der das AVL-Kriterium erfüllt, lässt sich in einer das Rot-Schwarz-Kriterium erfüllenden Weise einfärben.[28][29]

Es gibt aber Rot-Schwarz-Bäume, die das AVL-Kriterium nicht erfüllen. Die nebenstehende Abbildung zeigt zum Beispiel einen Rot-Schwarz-Baum mit 6 Knoten und der externen Pfadlängensumme 21, während 20 die größte externe Pfadlängensumme bei AVL-Bäumen (und zugleich die kleinstmögliche für alle Binärbäume) dieser Knotenzahl ist. Konsequenterweise ist auch die Worst-Case-Höhe des AVL-Baums kleiner als die des Rot-Schwarz-Baums, und zwar asymptotisch um den Faktor (2 log2 Φ)−1 ≈ 0,720. Allgemein werden AVL-Bäume als besser balanciert und ihr Suchverhalten als günstiger angesehen.
Die Laufzeiten für alle angeführten Operationen unterscheiden sich im Mittel und im Worst Case asymptotisch nur um einen konstanten Faktor, gehören also derselben Komplexitätsklasse an. Der Rot-Schwarz-Baum bietet allerdings amortisiert konstante Einfüge- und Löschkosten (jeweils nur Rebalancierung – ohne Navigation). Beim AVL-Baum sind nur die Einfügekosten amortisiert, die Löschkosten immerhin im Mittel konstant.
Realistische Anwendungssituationen mit Performancedaten und -vergleichen – auch mit weiteren Suchalgorithmen und Spielarten der Datenstrukturen – finden sich bei Ben Pfaff. Seine Ergebnisse zeigen in 79 Messungen unter anderem die sehr große Ähnlichkeit von AVL-Bäumen (AVL) und Rot-Schwarz-Bäumen (RB) mit Laufzeitverhältnissen AVL⁄RB zwischen 0,677 und 1,077 bei einem Median von ≈0,947 und einem geometrischen Mittelwert von ≈0,910.
Der Speicherplatzbedarf ist praktisch identisch: 1 Bit für das Rot-Schwarz-Attribut gegenüber 2 Bits[Anm. 16] für den AVL-Balance-Faktor. Während die Balance-Faktoren eines AVL-Baums direkt von seiner (graphentheoretischen) Gestalt abhängen, sind bei Rot-Schwarz-Bäumen derselben Gestalt – außer bei den Minimalbäumen gerader Höhe – unterschiedliche Einfärbungen möglich (s. Abschnitt Anzahlen von Rot-Schwarz-Bäumen). Dabei wirken sich die Unterschiede der Einfärbungen nur auf die Modifikations- und nicht auf die Navigationsoperationen aus. Des Weiteren kann jede mögliche Gestalt eines AVL-Baums durch gezielte Einfügungen auch hergestellt werden. Bezogen auf die Baumform gilt dies auch für Rot-Schwarz-Bäume; es gibt aber Baumformen, bei denen durchaus regelkonforme Einfärbungen in einem reinen Einfügeszenario nicht bewirkt werden können.
Eine Folge dieser etwas größeren Freiheitsgrade ist, dass im Rot-Schwarz-Baum die für die Einfügung oder Löschung erforderlichen Farbänderungen und Rotationen schon während des Suchvorgangs – also beim Abstieg – vorgenommen werden können.[30] Diese »Top-Down-Strategie«[31] ist bspw. für nebenläufige und persistente Programmierung interessant.[Anm. 17][32]
So bleibt beim Einfügen der frisch eingefügte Knoten rot. Das bedeutet, dass eine zugehörige Suchfunktion im Abstieg den Baum entlang dem betroffenen Pfad (in logarithmischer Zeit) so vorbereiten kann, dass das endgültige Einfügen unmittelbar bei einem schwarzen Elter in Form eines roten Knotens geschehen oder eben (nach gfl. Inspektion des Elters) auch unterbleiben kann. Genauso kann beim Löschen eine (andere) Suchfunktion den Baum im Abstieg so vorbereiten, dass der zu löschende Knoten rot ist. In beiden Fällen bleibt der Baum sowohl beim Durchführen wie beim Unterlassen der Modifikation ein gültiger Rot-Schwarz-Baum, einer Modifikation, die beim Einfügen nur aus dem Setzen eines einzigen Zeigers besteht und beim Löschen nur geringfügig komplizierter ist. Demgegenüber gibt es beim AVL-Baum Baumformen, bei denen die Entscheidung betreffend den Vollzug der Modifikation nicht mit derart geringer Implikation offen gehalten werden kann.
Verwendung von Rot-Schwarz-Bäumen[Bearbeiten | Quelltext bearbeiten]
Im Java Development Kit sind die Klassen TreeSet[33] und TreeMap[34] als Rot-Schwarz-Bäume implementiert. Sie stellen geordnete Mengen bzw. geordnete Dictionarys zur Verfügung.
Weitere Bäume[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Boston 2004, ftp.gnu.org (PDF gzip; 1662 kB; abgerufen am 13. Januar 2019).
- Ben Pfaff: Performance Analysis of BSTs in System Software. Stanford University, 2004, stanford.edu (PDF; 316 kB).
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7, S. 273–301.
- Robert Sedgewick: Algorithmen in C++. Addison-Wesley, 1992, ISBN 3-89319-462-2, S. 260–270 (englisch).
- Robert Sedgewick, Kevin Wayne: Algorithms Fourth Edition. Pearson Education, 2011, ISBN 978-0-321-57351-3, S. 432–447.
- Andrew Binstock, Jon Rex: Practical Algorithms for Programmers. Addison-Wesley Professional, 1995, ISBN 0-201-63208-X.
- Kurt Mehlhorn: Datenstrukturen und effiziente Algorithmen. Teubner Stuttgart 1988, ISBN 3-519-12255-3.
- Kurt Mehlhorn, Peter Sanders: Algorithms and Data Structures. The Basic Toolbox. Springer, Berlin / Heidelberg 2008, ISBN 978-3-540-77977-3, doi:10.1007/978-3-540-77978-0.
- Roger Whitney (San Diego State University): CS 660: Red–Black tree notes
- Mathworld: Red–Black Tree
Weblinks[Bearbeiten | Quelltext bearbeiten]
Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Diese Abschätzung ist scharf (s. Abschnitt Höhenbeweis)
und für wegen
- .
- ↑ Werden nämlich die NIL-Knoten als minimale Rot-Schwarz-Knoten implementiert, so brauchen sie Speicher für zwei Kindzeiger, ggf. einen Elterzeiger, das Feld für die Farbe und ein Erkennungsfeld für die Eigenschaft »NIL-Knoten«. Bei Schlüssel tragenden Knoten braucht man NIL-Knoten, womit sich der Rot-Schwarz-Overhead mehr als verdoppelt. Die Verknüpfungen der NIL-Knoten mit den Schlüssel tragenden Knoten (bspw. bei den Rotationen) sind überdies zu pflegen, so dass sich auch die Laufzeit verlängert. Das bedeutet im Ergebnis einen erheblichen Aufwand für das Aufzeichnen und Pflegen von Informationen, die für die nachfolgenden Algorithmen nicht gebraucht werden oder sich unmittelbar aus den anderen Informationen herleiten lassen.
- ↑ Dabei ist
dir == LEFTSchlüssel von < Schlüssel von .
S. a. Binärer Suchbaum#Suchen, wenn Duplikate zulässig. - ↑ Die Kurzschreibweise mit dem Pfeil
->ist erklärt im Artikel Verbund (Datentyp). - ↑ a b c Man beachte die in der Programmiersprache C festgelegte Art der Auswertung der
Disjunktion: (X == NIL)|| (X->color == BLACK)bzw. der Konjunktion: (X != NIL)&& (X->color == RED)die im Fall
X == NILdie zweite BedingungX->color == BLACKresp.X->color == REDnicht auswertet, sondern sofort zumelse-Zweig verzweigt. Im Beispielcode sind die entsprechenden Zeilen gelb hinterlegt.
Zusätzliche Bemerkung:
Die Schwarzhöhe 0 kommt nur in der ersten Iteration der Reparaturschleife vor. Bei den höheren Iterationsstufen ist die Schwarzhöhe aller besuchten KnotenXpositiv, somit auchX != NIL– und dieser Teil der Abfrage kann weggelassen werden.
Weiß man andererseits, dass die Schwarzhöhe eines Knotens 0 ist, dann weiß man auch, dass er, wenn er existiert, nur rot sein kann.
Damit lässt sich also die genannte Konjunktion/Disjunktion nach Herausziehen der ersten Iteration auf folgende Weise vereinfachen:erste Iteration: if (X != NIL)(welches X->color == REDdort immer impliziert)höhere Iteration: if (X->color == RED)(da dort immer X != NIL) - ↑ a b c d In der ersten Iterationsstufe ist der Teilbaum leer. Wenn die Knoten mit Elterzeiger implementiert werden, dann ist nach der Rotation der Elterzeiger dieses Teilbaums bei allen Iterationsstufen außer der ersten anzupassen.
- ↑ a b Wegen der Gleichsetzungen
LEFT ≡ 0undRIGHT ≡ 1spiegelt die logische Negation- nicht-
dir ≡ !dir ≡ 1−dir
LEFTRIGHT. Dabei istdir = (N == P->right)die Kindesrichtung von .
Im Kontext der Farben spricht man bei Zuweisungen à laRED :≡ !BLACKundBLACK :≡ !REDvon »Invertierung«. - nicht-
- ↑ Im Fall, dass die RB-Software die Benutzerdaten nicht kennt und trotzdem generisch sein muss, sind an Stelle der Benutzerdaten die RB-Daten zu vertauschen, so dass der (wirklich zu löschende) Knoten (mit dem Schlüssel und den Benutzerdaten von ) maximal ein RB-Kind hat. Bei dieser Vorgehensweise bleiben auch bspw. Zeiger auf gültige Knoten gültig.
- ↑ Um der Kürze der Aufschreibung willen wird im Beispielcode einige Male
gotoverwendet. Es ist leicht, dies durch Verdoppelung des Codes zu vermeiden. - ↑ Zu Beginn jedes Iterationsschritts hat das Geschwister die Schwarzhöhe .
- ↑ Wenn die Knoten mit Elterzeiger implementiert werden, dann ist der Elterzeiger des Knotens in allen Iterationen anzupassen, da die Schwarzhöhe von auch in der ersten Iteration ≥ 1 ist.
- ↑ Diese Minimalbäume spielen bei den Rot-Schwarz-Bäumen eine ähnliche Rolle wie die Fibonacci-Bäume bei den AVL-Bäumen.
- ↑ Die Wurzel eines minimalen Rot-Schwarz-Baums ungerader Höhe kann natürlich auch schwarz sein.
- ↑ Diese RB-Bäume gestatten darüber hinaus nur eine einzige Einfärbung, sind aber nicht die einzigen RB-Bäume mit dieser Eigenschaft.
Zur Höhe gibt es Formen von Minimalbäumen, da die Position des längsten Pfades der Position eines externen Blattes des vollständigen Binärbaums der Höhe entspricht und durch diese Position die Lage aller anderen Knoten bestimmt ist. (Die Abbildung zeigt die äußerste linke Position.) - ↑ Als eine Datenstruktur, die im homogenen Arbeitsspeicher (Hauptspeicher) untergebracht ist, ist der Rot-Schwarz-Baum durch dessen Größe beschränkt, also auch die Höhe des Baums und die Längen der Pfade von Blatt zu Wurzel.
Der Programmierer wird seinen Anwendern gegenüber eher die Knotenzahl einschränken als die Baumhöhe, die für den Anwender eher zufälliger Natur ist und ihn normalerweise nicht interessiert.
Die folgende Tabelle gibt zu jeder Knotenzahl eine Höhenangabe zurück, die von einem Rot-Schwarz-Baum mit Elementen nicht überschritten wird. Gängig sind Hauptspeicher mit 32 Bit und 64 Bit breiten virtuellen 8-Bit-Byte-Adressen. Da in einem 32-Bit-Adressraum maximal Bytes untergebracht werden können und ein Knoten mindestens 2 Kind-Zeiger à je 4 Bytes benötigt, kann bei Benutzerdaten (Schlüssel + Wert) von Bytes pro Knoten ein Baum mit maximal Knoten untergebracht werden; bei sind das Wie die Tabelle zeigt, kann im 32-Bit-Adressraum die Höhe durch einen Rot-Schwarz-Baum unmöglich überschritten werden.
Für einen Adressraum mit 8 Byte breiten Adressen und Byte Benutzerdaten hat man so dass bleibt und beim Einsatz von Bytes für den Elter-Stapel dieser nicht überlaufen kann.Umfang von Rot-Schwarz-Bäumen Anzahl Knoten Baumhöhe Nutzlänge 32-Bit-Adressen ⋮ ⋮ ⋮ 33554429 47 120 50331645 48 77 67108861 49 56 100663293 50 34 134217725 51 24 201326589 52 13 268435453 53 8 402653181 54 2 536870909 55 0 64-Bit-Adressen ⋮ ⋮ ⋮ 72057594037927933 109 240 108086391056891901 110 154 144115188075855869 111 112 216172782113783805 112 69 288230376151711741 113 48 432345564227567613 114 26 576460752303423485 115 16 864691128455135229 116 5 1152921504606846973 117 0 Mit den Bezeichnungen im Text ist eine Maßgabe, die so knapp wie möglich unterhalb der Knotenzahl des nächstgrößeren Minimalbaums bleibt. Ist der Speicherbedarf für alle Knoten gleich, können die Benutzerdaten pro Knoten maximal
im 32-Bit-Adressraum (4 Bytes/Adresse) im 64-Bit-Adressraum (8 Bytes/Adresse)
Bytes umfassen.
Fazit
Ist der Stapelspeicher
struct RBnode* Parents[]für die Elter-Zeiger bei einem 32-Bit-Adressraum auf wenigstens Einträge mit insgesamt Bytes ausgelegt, so kann er unmöglich überlaufen.
Dasselbe gilt bei einem 64-Bit-Adressraum für und einem Elter-Stapel der Größe Bytes.
Bevor nämlich in beiden Fällen der Elter-Stapel überläuft, ist der Adressraum schon geplatzt.
Ben Pfaff hat#define RB_MAX_HEIGHT 128. - ↑ oder auch nur 1 Bit (s. AVL-Implementierung)
- ↑ Die Sperren, die bei einem der Veränderung unterworfenen Baum der Erhaltung seiner Konsistenz dienen, können bei der Top-Down-Strategie von der Wurzel beginnend zu den Blättern fortschreitend gesetzt werden. Halten sich alle den Baum bearbeitenden Prozesse an solche (und ggf. weitere) Protokolle, kann ein Deadlock vermieden werden.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Rudolf Bayer: Symmetric Binary B-Trees. Data Structure and Maintenance Algorithms. In: Acta Informatica. 1. Jahrgang, 1972, S. 290–306, doi:10.1007/BF00289509 (englisch).
- ↑ Leo J. Guibas, Robert Sedgewick: A Dichromatic Framework for Balanced Trees. In: Proceedings of the 19th Annual Symposium on Foundations of Computer Science. IEEE Computer Society, 1978, S. 8–21 (englisch).
- ↑ Der Text folgt Ben Pfaff: An Introduction to Binary Search Trees and Balanced Trees. Zu anderen Varianten der Forderungen s. die Anmerkung NIL-Knoten.
- ↑ bei Ben Pfaff non-branching node
- ↑ Bei Ben Pfaff ist die Schwarzhöhe eines Knotens die einheitliche Anzahl schwarzer Knoten auf allen Pfaden zu den Pfadenden im von ihm gewurzelten Teilbaum.
- ↑ Mehlhorn 2008 S. 155 färbt die Kanten rot/schwarz und zählt als Schwarztiefe (englisch black depth) eines Knotens die Zahl der schwarzen Kanten von ihm zur Wurzel.
- ↑ a b Einige Autoren fordern noch, dass die Wurzel des Baums schwarz zu färben sei. Nicht jedoch z. B. Mehlhorn 2008 und Sedgewick. Tatsächlich ist diese Forderung ohne merkliche Bedeutung für das Laufzeitverhalten und stört die Rekursivität der Algorithmen etwas. Nun verletzt die Umfärbung einer roten Wurzel in schwarz keine der anderen Forderungen. In den Algorithmen für Einfügung und Löschung kann man jedoch mit einer Fallunterscheidung weniger auskommen, wenn man bei einem roten Knoten immer einen Elterknoten voraussetzen kann.
- ↑ a b J. R. Driscoll, N. Sarnak, D. D. Sleator, R. E. Tarjan: Making Data Structures Persistent. In: Journal of Computer and System Sciences. Band 38, No. 1, 1989 (cs.cmu.edu)
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7.
- ↑ a b Die Implementierung kommt auf diese Weise (wie auch Ben Pfaff – zumindest konzeptionell) ohne einen bei den Knoten gespeicherten Elterzeiger aus.
Zur Größe eines solchen Stapels s. Stapelgröße.
Werden allerdings mehrere Zugriffspfade zum selben Suchbaum benötigt, dann kann die Implementierung mit Elterzeiger bessere Laufzeiten ergeben als die Wiederholung von Suchvorgängen. - ↑ Ben Pfaff bringt außer der Variante des Textes auch eine Variante mit einem ersten eingefügten Knoten schwarzer Farbe.
- ↑ Diese Aufteilung findet sich u. a. bei Ben Pfaff.
- ↑ a b Eine andere Möglichkeit ist, den Schleifenrumpf der
do while-Schleife in zwei Versionen hinzuschreiben, in einer für die Kindesrichtung links und in einer für rechts (so bspw. Ben Pfaff). - ↑ a b Für die Vorteile der iterativen Programmierung hinsichtlich Platz und Zeit gegenüber einer rekursiven Programmierung s. a. Binärer Suchbaum#Iterative Programmierung. Darüber hinaus erzwingt erstere eine genauere Beachtung der Knoteneigenschaften.
- ↑ Diese Vorgehensweise wurde zum ersten Mal von T. Hibbard in 1962 vorgeschlagen, zitiert nach Robert Sedgewick, Kevin Wayne: Algorithms Fourth Edition. Pearson Education, 2011, ISBN 978-0-321-57351-3, S. 410 (englisch, abgerufen am 25. März 2018)
- ↑ Die Aufteilung entspricht Roger Whitney.
- ↑ Auf eine andere Aufteilung (der Bedingungen) der Fälle, aber im Ergebnis ebenfalls auf die Gesamtzahl 6, kommt University of Science and Technology of China (zitiert nach stackoverflow.com).
- ↑ Robert Endre Tarjan: 4. Search Trees 5. Linking and Cutting Trees. In: SIAM (= Data structures and network algorithms). 1983, ISBN 978-0-89871-187-5, S. 45–70, doi:10.1137/1.9781611970265.ch5.
- ↑ Donald E. Knuth: The Art of Computer Programming, Band 3, Sorting and Searching, 2. Auflage, Addison-Wesley, 1998, S. 474
- ↑ Guy Edward Blelloch, Daniel Ferizovic, Yihan Sun: Just Join for Parallel Ordered Sets. Hrsg.: ACM (= Symposium on Parallel Algorithms and Architectures, Proc. of 28th ACM Symp. Parallel Algorithms and Architectures (SPAA 2016)). 2016, ISBN 978-1-4503-4210-0, S. 253–264, doi:10.1145/2935764.2935768, arxiv:1602.02120.
- ↑ Sedgewick 2011 S. 444 Proof sketch
- ↑ Gleichheit am oberen Rand gilt für minimale RB-Bäume RB2k gerader Baumhöhe mit Knoten und nur für diese. Damit ist die Ungleichung geringfügig genauer als das weitverbreitete z. B. in Cormen S. 264.
- ↑ Mehlhorn und Sanders widmen dem Thema in Mehlhorn 2008 das Kapitel 7.4 Amortized Analysis of Update Operations mit dem Theorem 7.3, S. 158:
- „Consider an (a,b)-tree with b ≥ 2a that is initially empty. For any sequence of n insert or remove operations, the total number of split or fuse operations is O(n).“
- „Für eine beliebige Folge von Einfüge- und Löschoperationen in einen anfänglich leeren Rot-Schwarz-Baum ist die Anzahl der Farbwechsel und Rotationen in .“
- ↑ Lightweight Java implementation of Persistent Red-Black Trees
- ↑ Mehlhorn 1988 S. 193
- ↑ Wenn man die zwei Wahlmöglichkeiten bei 3 Kindern auf eine (bspw. auf die erste, die obere) einschränkt, kommt man zu den LLRB (Abkürzung für englisch left-leaning red–black) Bäumen, die im Wesentlichen dieselben informationstheoretischen Eigenschaften haben, bei deren Implementierung aber laut Sedgewick weniger Fälle zu unterscheiden sind (s. Robert Sedgewick. Left-leaning Red–Black Trees und PDF).
- ↑ Mehlhorn 1988 S. 187
- ↑ Paul E. Black: Red-black tree. In: Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology, 13. April 2015, abgerufen am 2. Juli 2016 (englisch).
- ↑ s. „One should be able to color any AVL tree, without restructuring or rotation, to transform it into a Red-Black tree.“ Junghyun Chae in AVL Trees vs. Red-Black Trees? abgerufen am 14. Oktober 2015 und Beweis in AVL-Baum#VergleichRB.
- ↑ Red Black Trees. In: eternallyconfuzzled.com. Archiviert vom am 27. September 2007; abgerufen am 14. Oktober 2015 (englisch). (Eternally Confuzzled)
- ↑ Mehlhorn 1988 S. 197–198.
- ↑ s. a. Comparison of Binary Search Trees abgerufen am 14. Oktober 2015; oder Paul Callahan in AVL Trees vs. Red-Black Trees? abgerufen am 14. Oktober 2015
- ↑ Java Class TreeSet auf docs.oracle.com
- ↑ Java Class TreeMap auf docs.oracle.com


















































































































![{\displaystyle {\bigl [}<2\log _{2}(n+1)\;{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0c1043c587524d2a645896481b77387cb1ca96e)



































