Über das Gleichgewicht ebener Flächen

Archimedes hebt die Erde aus den Angeln, Illustration aus Alexandrini Collectionis von Friedrich Otto Hultsch, Berlin, 1878

Über das Gleichgewicht ebener Flächen (griech. Περὶ ἐπιπέδων ἱσορροπιῶν, perí epipédōn isorropiôn) ist ein Werk von Archimedes in zwei Bänden. Buch I enthält einen Beweis des Hebelgesetzes und gipfelt in Propositionen über den Schwerpunkt des Dreiecks und des Trapezes. Buch II enthält zehn Propositionen und untersucht die Schwerpunkte von Parabelsegmenten.

Laut Pappos veranlassten die Untersuchungen der Hebelwirkung Archimedes zu dem Ausspruch: „Gebt mir einen festen Punkt und ich hebe die Welt aus den Angeln“ (griech. δός μοί ποῦ στῶ καὶ κινῶ τὴν γῆν, dṓs moi poû stṓ kaí kinô tḗn gên), obwohl andere antike Zeugnisse hinsichtlich der Herkunft des Spruchs nicht eindeutig sind.

Überblick

Der Hebel und dessen Wirkungsweise waren bereits vor Archimedes bekannt. Das frühere Werk Fragen der Mechanik, das einst Aristoteles zugeschrieben wurde, aber höchstwahrscheinlich von einem seiner Nachfolger verfasst wurde, enthält einen losen Beweis für das Hebelgesetz, ohne den Begriff des Schwerpunkts zu verwenden. Ein kurzes Werk mit dem Titel The Book of the Balance, das Euklid zugeschrieben wird, enthält ebenfalls einen mathematischen Beweis des Gesetzes, ebenfalls ohne Bezug auf den Schwerpunkt.

Im Gegensatz dazu ist bei Archimedes der Begriff des Schwerpunkts entscheidend. In Über das Gleichgewicht ebener Flächen I mit sieben Axiomen und fünfzehn Propositionen wird der Schwerpunkt sowohl für kommensurable als auch inkommensurable Größen verwendet, um das Hebelgesetz zu begründen, auch wenn einige behaupten, dass dies nicht zufriedenstellend ist. Archimedes bestimmt dann den Schwerpunkt des Parallelogramms und des Dreiecks und beendet das erste Buch mit einem Beweis über den Schwerpunkt des Trapezes.

Das Buch Über das Gleichgewicht ebener Flächen II enthält zehn Propositionen über den Schwerpunkt von Parabelsegmenten und untersucht diese Segmente, indem er sie durch Rechtecke mit gleicher Fläche ersetzt. Ermöglicht wird dieser Ansatz durch Ergebnisse aus seinem Werk Quadratur der Parabel.

Inhalte

Buch I

Die erste Hälfte von Buch I befasst sich mit den Eigenschaften der Waage und dem Hebelgesetz, während die zweite Hälfte den Schwerpunkt von ebenen Grundfiguren behandelt. Die Herleitung des Hebelgesetzes stützt sich insbesondere auf das erste Axiom, das besagt, dass „gleiche Gewichte in gleichen Abständen im Gleichgewicht sind“. In den Propositionen 4 und 5 erweitert Archimedes dieses Axiom, indem er beweist, dass der Schwerpunkt eines jeden Systems, das aus einer geraden Anzahl gleicher, gleichmäßig verteilter Gewichte besteht, in der Mitte zwischen den beiden mittleren Gewichten liegt. Mit Hilfe dieser Theoreme beweist Archimedes dann das Hebelgesetz in Proposition 6 (für kommensurable Fälle) und Proposition 7 (für inkommensurable Fälle).

Theorem

Gewichte und Hebel in einem Verhältnis von 4:3.

In moderner Ausdrucksweise: Bei zwei ungleichen, aber verhältnismäßigen Gewichten und einem Hebelarm, der in zwei ungleiche, aber verhältnismäßige Abschnitte unterteilt ist (siehe nebenstehende Skizze), befindet sich das System im Gleichgewicht, wenn die Größen $A$ und $B$ an den Punkten $E$ bzw. $D$ angesetzt werden und die Gewichte umgekehrt proportional zu den Längen sind:

$A:B={\overline {CD}}:{\overline {EC}}\,$

Nach heutiger Lehre entspricht dieses Gleichgewicht sich aufhebenden Drehmomenten um den Drehpunkt.

Beweis

Nehmen wir an, dass Linien (Hebel) und Gewichte so konstruiert sind, dass sie ein gemeinsames Maß (oder eine Einheit) $n$ und ein Verhältnis von $4:3$ haben. Nun verdoppeln wir die Länge von ${\overline {ED}}$, indem wir den längeren Arm auf der linken Seite und den kürzeren Arm auf der rechten Seite duplizieren.

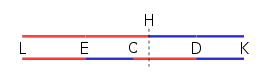
Zur Veranschaulichung ordnen wir die Längen so an, dass ${\overline {CD}}$ an ${\overline {LE}}$ angrenzt (die beiden roten Zeilen zusammen), und stellen sie dem Original gegenüber:

Es ist klar, dass beide Linien doppelt so lang sind wie die ursprüngliche Linie ${\overline {ED}}$, dass ${\overline {LH}}$ seinen Mittelpunkt bei $E$ hat, und dass ${\overline {HK}}$ seinen Mittelpunkt bei $D$ hat. Außerdem ist zu beachten, dass ${\overline {EH}}$ (das gleich ${\overline {CD}}$ ist) das gemeinsame Maß (bzw. die Einheit) $n$ genau so oft enthält wie ${\overline {EC}}$ und im weiteren Sinne auch ${\overline {CH}}$. Es bleibt also zu beweisen, dass $A$, das bei $E$ angelegt wird, und $B$, das bei $D$ angelegt wird, ihren Schwerpunkt bei $C$ haben werden.

Da also das Verhältnis ${\overline {LH}}:{\overline {HK}}$ die ursprünglichen Abstände ${\overline {CD}}$ und ${\overline {EC}}$ verdoppelt hat, teilen wir die Größen $A$ und $B$ in ähnlicher Weise in ein Verhältnis von $8:6$ (eine Transformation, die ihr ursprüngliches Verhältnis von $4:3$ beibehält) und richten sie so aus, dass die Einheiten $A$ (rot) auf $E$ zentriert sind, während die Einheiten $B$ (blau) auf $D$ zentriert sind.

Da nun eine gerade Anzahl gleicher Gewichte, die gleichmäßig verteilt sind, ihren Schwerpunkt zwischen den beiden mittleren Gewichten haben, liegt $A$ in der Tat bei $E$ und $B$ bei $D$, wie es die Proposition verlangt. Außerdem besteht das Gesamtsystem aus einer geraden Anzahl gleicher Gewichte, die gleichmäßig verteilt sind, und daher muss nach demselben Gesetz $C$ der Schwerpunkt des gesamten Systems sein. Das System neigt sich also nicht, sondern befindet sich im Gleichgewicht.

Buch II

Titelblatt von Heibergs Ausgabe des Buch II

Das Hauptziel des zweiten Buches ist die Bestimmung des Schwerpunkts eines beliebigen Teils eines Parabelsegments, wie in Proposition 8 gezeigt.

Das Buch beginnt mit einem einfacheren Beweis des Hebelgesetzes in Proposition 1, wobei Archimedes Ergebnisse aus der Quadratur der Parabel Bezug nimmt Archimedes beweist die nächsten sieben Propositionen, indem er das Konzept des Schwerpunkts und die Eigenschaften der Parabel mit den Ergebnissen aus Über das Gleichgewicht ebener Flächen I kombiniert. Insbesondere folgert er, dass zwei flächengleiche Parabeln ihren Schwerpunkt in gleichem Abstand von einem Punkt haben, und ersetzt später ihre Flächen durch Rechtecke mit gleicher Fläche.

Die letzten beiden Propositionen 9 und 10 sind schwer verständlich und befassen sich mit der Bestimmung des Schwerpunkts einer Figur, die durch einen Kegelstumpf von einem beliebigen Parabelsegment abgeschnitten ist.

Späterer Einfluss

Archimedes' mechanische Werke, darunter Über das Gleichgewicht ebener Flächen, waren in der Antike bekannt, wurden aber wenig gelesen. Sowohl Heron als auch Pappos beziehen sich in ihren Werken zur Mechanik auf Archimedes, vor allem in ihren Diskussionen über den Schwerpunkt und die Hebelwirkung. Einige römische Autoren, wie Vitruv, kannten ebenfalls Archimedes' Werk.

Im Mittelalter waren einige arabische Autoren mit Archimedes' Arbeiten über Gleichgewicht und Schwerpunkt vertraut und erweiterten sie; im lateinischen Westen blieben diese Ideen jedoch weitgehend unbekannt. Erst in der späten Renaissance verbreiteten sich die in Über das Gleichgewicht der ebenen Flächen dargestellten Ergebnisse. Insbesondere Archimedes' mathematischer Ansatz zur Physik wurde zum Vorbild für spätere Wissenschaftler wie Guidobaldo del Monte, Bernardino Baldi, Simon Stevin und Galileo Galilei.

Das Konzept des Schwerpunkts erreichte in der ersten Hälfte des 17. Jahrhunderts einen hohen Grad an Verfeinerung, insbesondere in den Werken von Evangelista Torricelli und Christiaan Huygens, und spielte eine entscheidende Rolle bei der Entwicklung der klassischen Mechanik.

Kritik

Eine Reihe von Forschern hat auf Ungereimtheiten im ersten Buch von „Über das Gleichgewicht ebener Flächen“ hingewiesen. John Lennart Berggrenstellt die Echtheit von fast der Hälfte des ersten Buches in Frage und verweist beispielsweise auf die Redundanz der Propositionen 1–3 und 11–12. Er folgt jedoch Eduard Jan Dijksterhuis in der Zurückweisung der Kritik von Ernst Mach an Proposition 6, die in der Tat beweist, dass „wenn ein System von Gewichten, die an einem Waagebalken aufgehängt sind, im Gleichgewicht ist, wenn es in einem bestimmten Punkt aufliegt, dann bewahrt jede Umverteilung dieser Gewichte, die ihren gemeinsamen Schwerpunkt bewahrt, auch das Gleichgewicht“.

Außerdem erscheint die Proposition 7 des ersten Buches in seiner jetzigen Form unvollständig, so dass Archimedes im ersten Buch das Hebelgesetz streng genommen nur für kommensurable Größen demonstriert. Buch II von Über das Gleichgewicht ebener Flächen ist von diesen Unzulänglichkeiten nicht betroffen, da der Hebel mit Ausnahme des ersten Satzes überhaupt nicht behandelt wird. In den überlieferten Werken des Archimedes gibt es keine Definition des Schwerpunkts, was es nach Ansicht einiger Wissenschaftler schwierig macht, die logische Struktur einiger seiner Argumente in Über das Gleichgewicht ebener Flächen nachzuvollziehen (oder zu rechtfertigen).