Hessesche Normalform
Die hessesche Normalform, Hesse-Normalform oder hessesche Normalenform ist in der Mathematik eine spezielle Form einer Geradengleichung oder Ebenengleichung. Die hessesche Normalform dient häufig dazu, den Abstand eines Punktes zu einer Geraden (im ) oder einer Ebene (im ) zu berechnen. Sie ist nach dem deutschen Mathematiker Otto Hesse benannt.
Hessesche Normalform einer Geradengleichung[Bearbeiten | Quelltext bearbeiten]
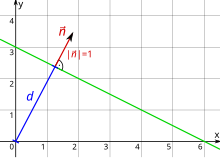
Vektorform[Bearbeiten | Quelltext bearbeiten]
In der hesseschen Normalform wird eine Gerade in der euklidischen Ebene durch einen normierten Normalenvektor (Normaleneinheitsvektor) der Geraden, sowie ihren Abstand vom Koordinatenursprung beschrieben. Eine Gerade besteht dann aus denjenigen Punkten in der Ebene, deren Ortsvektoren die Gleichung
erfüllen. Hierbei bezeichnet das Skalarprodukt.
Der Normalenvektor ist ein Vektor, der orthogonal zu der Geraden ist, d. h. einen rechten Winkel mit ihr bildet.
Als Normaleneinheitsvektor muss er die Länge besitzen und er muss vom Koordinatenursprung in Richtung der Geraden zeigen, es muss also gelten.
In der hesseschen Normalform werden demnach die Punkte der Geraden implizit dadurch definiert, dass das Skalarprodukt aus dem Ortsvektor eines Geradenpunkts und dem Normalenvektor der Geraden gleich dem Abstand der Geraden vom Ursprung ist. Ein Punkt, dessen Ortsvektor die Gleichung nicht erfüllt, liegt für auf derjenigen Seite der Geraden, in die der Normalenvektor zeigt, und ansonsten auf der anderen Seite. Der Koordinatenursprung befindet sich immer auf der negativen Seite der Geraden, sofern sie keine Ursprungsgerade ist.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Ist ein Normaleneinheitsvektor einer Geraden und der Abstand der Geraden vom Ursprung, so erhält man die Normalform
- .
Jede Wahl von , die diese Gleichung erfüllt, beispielsweise oder , entspricht dann einem Geradenpunkt.
Berechnung[Bearbeiten | Quelltext bearbeiten]
Aus der Normalenform einer Geradengleichung mit Stützvektor und Normalenvektor lässt sich ein normierter und vorzeichenbehafteter Normalenvektor der Geraden durch
bestimmen. Der Abstand der Geraden vom Ursprung kann dann durch
ermittelt werden. Dieser Abstand entspricht gerade der Länge der Orthogonalprojektion des Vektors auf die Ursprungsgerade mit Richtungsvektor .
Aus den weiteren Formen von Geradengleichungen, der Koordinatenform, der Achsenabschnittsform, der Parameterform und der Zweipunkteform, wird zunächst die zugehörige Normalenform der Geraden ermittelt (siehe Berechnung der Normalenform) und daraus dann die hessesche Normalform.
Abstandsberechnung[Bearbeiten | Quelltext bearbeiten]
Mit Hilfe der hesseschen Normalform kann der Abstand eines beliebigen Punkts in der Ebene von einer Geraden einfach dadurch berechnet werden, dass der Ortsvektor des Punkts in die Geradengleichung eingesetzt wird:
- .
Dieser Abstand ist vorzeichenbehaftet: Für liegt der Punkt auf derjenigen Seite der Geraden, in die der Normalenvektor zeigt, ansonsten auf der anderen Seite.
Alternativ kann man den absoluten Betrag verwenden:
oder sogar den (nicht normierten) Normalenvektor benutzen:
Koordinatenform[Bearbeiten | Quelltext bearbeiten]
Die allgemeine Koordinatenform einer Geradengleichung ist
- .
Dividiert man diese Gleichung durch , erhält man die Hessesche Normalform der Koordinatengleichung:
- .
Eigenschaften:
Der Abstand eines Punktes von der Geraden ist
- , speziell: .
- ist ein Einheitsnormalenvektor der Geraden.
Ist die Geradengleichung in expliziter Form , so ist . Die zur y-Achse parallele Gerade mit der Gleichung hat die Hessesche Normalform .
Hessesche Normalform einer Ebenengleichung[Bearbeiten | Quelltext bearbeiten]

Darstellung[Bearbeiten | Quelltext bearbeiten]
Analog wird eine Ebene im dreidimensionalen Raum in der hesseschen Normalform durch einen normierten (möglicherweise mit einem Vorzeichen versehenen) Normalenvektor der Ebene sowie ihren Abstand vom Koordinatenursprung beschrieben. Eine Ebene besteht dann aus denjenigen Punkten im Raum, deren Ortsvektoren die Gleichung
erfüllen. Der Normalenvektor ist hier ein Vektor, der senkrecht auf der Ebene steht. Der Normalenvektor muss wiederum die Länge besitzen und vom Koordinatenursprung in Richtung der Ebene zeigen, es muss also gelten.
In der hesseschen Normalform werden demnach die Punkte der Ebene implizit dadurch definiert, dass das Skalarprodukt aus dem Ortsvektor eines Ebenenpunkts und dem Normalenvektor der Ebene gleich dem Abstand der Ebene vom Ursprung ist. Wiederum liegt ein Punkt, dessen Ortsvektor die Gleichung erfüllt, auf der Ebene. Gilt , dann liegt der Punkt auf derjenigen Seite der Ebene, in die der Normalenvektor zeigt, ansonsten auf der anderen Seite. Der Koordinatenursprung befindet sich immer auf der negativen Seite der Ebene, sofern sie keine Ursprungsebene ist.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Ist beispielsweise ein normierter Normalenvektor einer gegebenen Ebene und der Abstand der Ebene vom Ursprung , so erhält man als Ebenengleichung
- .
Jede Wahl von , die diese Gleichung erfüllt, beispielsweise oder , entspricht dann einem Ebenenpunkt.
Berechnung[Bearbeiten | Quelltext bearbeiten]
Aus der Normalenform einer Ebenengleichung mit Stützvektor und Normalenvektor lässt sich ein normierter und vorzeichenbehafteter Normalenvektor der Ebene wie im zweidimensionalen Fall durch
bestimmen. Der Abstand der Ebene vom Ursprung kann dann durch
ermittelt werden. Dieser Abstand entspricht wiederum der Länge der Orthogonalprojektion des Vektors auf die Ursprungsgerade mit Richtungsvektor .
Aus den weiteren Formen von Ebenengleichungen, der Koordinatenform, der Achsenabschnittsform, der Parameterform und der Dreipunkteform, wird zunächst die zugehörige Normalenform der Ebene ermittelt (siehe Berechnung der Normalenform) und daraus dann die hessesche Normalform.
Abstand[Bearbeiten | Quelltext bearbeiten]
Mit Hilfe der hesseschen Normalform kann der Abstand eines beliebigen Punkts im Raum von einer Ebene wiederum dadurch berechnet werden, dass der Ortsvektor des Punkts in die Ebenengleichung eingesetzt wird:
- .
Dieser Abstand ist wieder vorzeichenbehaftet: Für liegt der Punkt auf derjenigen Seite der Ebene, in die der Normalenvektor zeigt, ansonsten auf der anderen Seite.
Alternative Formulierung mit einem Stützvektor[Bearbeiten | Quelltext bearbeiten]
Obwohl häufig die Abstandsberechnung mithilfe der hesseschen Normalform mithilfe eines Abstandes zum Koordinatenursprung gelehrt wird, wird gelegentlich auf eine ähnliche hessesche Normalenform mit Stützvektor zurückgegriffen.[1]
Die hessesche Normalenform einer Ebene lautet dann
- ,
wobei ein Stützvektor der Ebene ist.
Abstandsformel[Bearbeiten | Quelltext bearbeiten]
Daraus ergibt sich dann die Abstandsformel für einen Punkt Q mit dem Ortsvektor von der Ebene mit dem Stützvektor und dem Normaleneinheitsvektor
- .
Verallgemeinerung für Hyperebenen[Bearbeiten | Quelltext bearbeiten]
Allgemein wird durch die hessesche Normalform eine Hyperebene im -dimensionalen euklidischen Raum beschrieben. Im -dimensionalen euklidischen Raum besteht eine Hyperebene entsprechend aus denjenigen Punkten, deren Ortsvektoren die Gleichung
erfüllen. Es wird dabei lediglich mit -komponentigen statt mit zwei- oder dreikomponentigen Vektoren gerechnet. Eine Hyperebene teilt den -dimensionalen Raum in zwei Teile, die Halbräume genannt werden. Ein Punkt, dessen Ortsvektor die Gleichung erfüllt, liegt genau auf der Hyperebene. Gilt , dann liegt der Punkt in demjenigen Halbraum, in den der Normalenvektor zeigt, ansonsten in dem anderen.
Geschichte[Bearbeiten | Quelltext bearbeiten]

Otto Hesse führte 1865 in seinem Buch Analytische Geometrie neben der allgemeinen Form einer Geradengleichung die Normalform
ein. Dabei sind die Winkel der Normalen durch den Nullpunkt gegenüber den Koordinatenachsen und der Abstand der Geraden vom Nullpunkt. Da ist, schreibt man heute
Analog ist die Normalform einer Ebene erklärt.
Hesse zeigt die wichtige geometrische Eigenschaft der Normalform: Man kann mit ihr auf einfache Weise den Abstand eines Punktes von einer Geraden oder einer Ebene bestimmen.
Diese vorteilhafte Art, eine Gerade oder Ebene zu beschreiben, wurde später von Autoren übernommen und als Hessesche Normalform bezeichnet[2].
In Hesses Buch ist auch die übliche Umrechnung der allgemeinen Form in die Normalform durch Multiplikation mit dem Faktor enthalten.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- O. Hesse: Vorlesungen aus der Analytischen Geometrie der graden Linie, des Punktes und des Kreises in der Ebene. E.B. Teubner, 1865.
- Alfred Clebsch, Dr. Ferdinand Lindemann: Vorlesungen über Geometrie , Springer-Verlag, 1891/2013, ISBN 3663157709, 9783663157700, S. 11.
- Lothar Papula: Mathematische Formelsammlung: Für Ingenieure und Naturwissenschaftler. Springer, 2009, ISBN 978-3-8348-9598-1.
- Harald Scheid, Wolfgang Schwarz: Elemente der Linearen Algebra und der Analysis. Springer, 2009, ISBN 978-3-8274-2255-2.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Anton Bigalke, Norbert Köhler (Hrsg.): Mathematik. Gymnasiale Oberstufe Berlin Grundkurs ma-3. Cornelsen Verlag, Berlin 2011, ISBN 978-3-06-040003-4, S. 137.
- ↑ M. Koecher, A. Krieg: Ebene Geometrie, Springer-Verlag, 2007, ISBN 354049328X, 9783540493280, S. 114.

























































