Potenz (Geometrie)

Der Begriff Potenz bezeichnet in der Geometrie ein spezielles, von Jakob Steiner 1826 eingeführtes Maß dafür, wie weit außerhalb oder innerhalb eines Kreises sich ein Punkt befindet[1]. Die Potenz eines Punktes bezüglich eines Kreises mit Mittelpunkt und Radius ist die reelle Zahl
Falls außerhalb des Kreises liegt, ist und gleich dem Quadrat der tangentialen Distanz von zum Kreis (siehe Bild). Dies folgt aus dem Satz des Pythagoras.
Falls auf dem Kreis liegt, ist .
Falls innerhalb des Kreises liegt, ist .
Steiner benutzte die Potenz eines Kreises, um zahlreiche Aussagen über Kreise und Kugeln zu beweisen. Z.B.:
- Bestimmung eines Kreises, der vier vorgegebene Kreise unter dem gleichen Winkel schneidet[2].
- Lösung des Apollonischen Problems
- Konstruktion der Malfatti-Kreise[3]: Bestimme zu einem Dreieck drei Kreise, die sich gegenseitig berühren und jeweils zwei Seiten berühren.
- Sphärische Version des Malfatti Problems[4]: Bestimme zu einem sphärischen Dreieck drei Kreise, die sich gegenseitig berühren und jeweils zwei Seiten des Dreiecks berühren.
- Auf einer Quadrik[5]: Bestimme zu drei ebenen Kurven auf einer Quadrik drei weitere ebene Kurven, die sich gegenseitig berühren und jeweils zwei der gegebenen Kurven berühren.
Als wesentliches Hilfsmittel verwendet Steiner Ähnlichkeitspunkte und die gemeinschaftliche Potenz zweier Kreise.
Der Begriff Potenz bezüglich eines Kreises lässt sich auf den Raum als Potenz einer Kugel übertragen.
Geometrische Bedeutung
[Bearbeiten | Quelltext bearbeiten]Außer den im ersten Bild mit Hilfe des Satzes von Pythagoras erkennbaren geometrischen Bedeutungen der Potenz, gibt es weitere Eigenschaften:
Orthogonalkreis
[Bearbeiten | Quelltext bearbeiten]
Zu einem Punkt außerhalb des Kreises gibt es zwei Berührpunkte auf dem Kreis (siehe Bild), die gleich weit von entfernt sind. Der Kreis mit als Mittelpunkt durch geht also auch durch und schneidet den Kreis senkrecht. Dies liefert eine weitere geometrische Bedeutung der Potenz:
- Der Kreis mit Mittelpunkt und Radius schneidet den Kreis senkrecht.

Falls der Radius des Kreises um ungleich ist, erhält man den Schnittwinkel der beiden Kreise mit Hilfe des Kosinussatzes (siehe Bild):
( und sind Normalen zu den Kreistangenten.)
Liegt in dem blauen Kreis, ist und damit immer ungleich .
Falls der Winkel vorgegeben wird, erhält man den Radius aus der quadratischen Gleichung
- .

Sekantensatz, Sehnensatz
[Bearbeiten | Quelltext bearbeiten]Im Sekantensatz und Sehnensatz spielt die Potenz eines Punktes die Rolle einer Invarianten:
- Sekantensatz: Liegt der Punkt außerhalb des Kreises und sind und die Schnittpunkte einer beliebigen Geraden durch mit dem Kreis, so ist , also unabhängig von der Gerade . Diese Aussage ist auch dann noch richtig, wenn und zusammenfallen (Sekanten-Tangenten-Satz).
- Sehnensatz: Sind und die Schnittpunkte einer beliebigen Geraden durch mit dem Kreis, so ist .
Potenzgerade
[Bearbeiten | Quelltext bearbeiten]Betrachtet man zu zwei vorgegebenen Kreisen (Mittelpunkte und Radien ), einen Punkt , so hat dieser die Potenz bezgl. des ersten Kreises und die Potenz bezgl. des zweiten Kreises. Bestimmt man die Gesamtheit aller Punkte, die bezgl. beider Kreise dieselbe Potenz besitzen, es ist also , so erhält man eine Gerade, die Potenzgerade der beiden Kreise.
Sekantensatz, Sehnensatz: einheitlicher Beweis
[Bearbeiten | Quelltext bearbeiten]Bei den Sätzen Sekantensatz, Sekanten-Tangenten-Satz und Sehnensatz spielt die Potenz eines Punktes als Invariante eine wesentliche Rolle. Diese Sätze lassen sich mit Hilfe von ähnlichen Dreiecken und dem Kreiswinkelsatz koordinatenfrei beweisen.

Der folgende einfache Beweis verwendet Vektorrechnung:
Es sei ein Punkt, ein Kreis mit dem Ursprung als Mittelpunkt und ein beliebiger Einheitsvektor. Die Parameter möglicher Schnittpunkte der Gerade (durch ) und dem Kreis können durch Einsetzen der Parameterdarstellung von in die Kreisgleichung bestimmt werden:
Aus dem Satz von Vieta ergibt sich:
- (unabhängig von !)
ist die Potenz von bezüglich des Kreises .
Wegen ergibt sich für die Punkte :
- , falls außerhalb des Kreises ist,
- , falls in dem Kreis liegt ( haben verschiedene Vorzeichen !).
Falls ist, ist eine Tangente und das Quadrat der tangentialen Distanz des Punktes zu dem Kreis .
Ähnlichkeitspunkte, gemeinschaftliche Potenz zweier Kreise
[Bearbeiten | Quelltext bearbeiten]Ähnlichkeitspunkte
[Bearbeiten | Quelltext bearbeiten]Ein wesentliches Werkzeug Steiners bei seinen Untersuchungen sind die Ähnlichkeitspunkte zweier Kreise[6].
Es seien
- zwei Kreise.
Eine zentrische Streckung (Ähnlichkeitsabbildung) , die auf abbildet, muss den Radius auf strecken (stauchen) und hat ihr Zentrum auf der Gerade (). Liegt das Zentrum zwischen ist der Streckfaktor . Im anderen Fall ist . In jedem Fall ist:
- .
setzt man ein und löst nach auf erhält man:
- .

Den Punkt
nennt man äußeren Ähnlichkeitspunkt und
inneren Ähnlichkeitspunkt.
(Um Nachzuweisen, dass die Streckung an mit dem Faktor den Kreis auf den Kreis abbildet, darf man annehmen, dass der Ursprung ist. Analog für die Streckung an .)
Im Fall ist .
Im Fall ist der Fernpunkt der Gerade und der Mittelpunkt von .
Im Fall berühren sich die Kreise in innerlich (beide Kreise auf einer Seite der gemeinsamen Tangente).
Im Fall berühren sich die Kreise in äußerlich (beide Kreise auf verschiedenen Seiten der gemeinsamen Tangente).
Ferner gilt:
- Liegen die zwei Kreise getrennt (die Kreisflächen haben keine Punkte gemeinsam), so gehen von den vier gemeinsamen Tangenten die äußeren durch und die inneren durch .
- Liegt ein Kreis in dem anderen, so liegen innerhalb beider Kreise.
- Die Punktepaare liegen harmonisch: Sie haben das Doppelverhältnis .
Der Satz von Monge zeigt, dass die äußeren Ähnlichkeitspunkte von drei getrennt liegenden Kreisen auf einer Gerade liegen.
Gemeinschaftliche Potenz zweier Kreise
[Bearbeiten | Quelltext bearbeiten]
Sind zwei Kreise, ihr äußerlicher Ähnlichkeitspunkt und eine Gerade durch , die die beiden Kreise in Punkten schneiden, so folgt aus der Eigenschaft von
und aus dem Sekantensatz (siehe oben)
Aus den drei Gleichungen folgt:
Also gilt:
- (unabhängig von !).
Das analoge Resultat erhält man für eine Sekante durch den inneren Ähnlichkeitspunkt .
Die Invarianten nennt Steiner gemeinschaftliche Potenz der beiden Kreise bezüglich ihrer Ähnlichkeitspunkte[7].
Jedes der Punktepaare und nennt man antihomolog. Die Paare und heißen homolog; sie sind Urbild-Bildpaare bezüglich der Ähnlichkeitsabbildung (Homologie).[8][9]
Anwendung: Bestimmung der Berührkreise zweier Kreise
[Bearbeiten | Quelltext bearbeiten]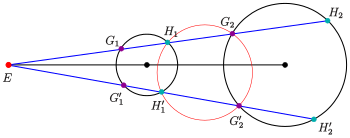

Legt man durch eine zweite Sekante (siehe Bild) gilt:
Mit dem Sekantensatz erkennt man:
- Die Punkte liegen auf einem Kreis.
Analog ergibt sich:
- Die Punkte liegen auf einem Kreis.
Da sich die Potenzgeraden dreier Kreise in einem Punkt schneiden (siehe: Artikel Potenzgerade) gilt:
- Die Sekanten schneiden sich auf der Potenzgerade der gegebenen Kreise.
Lässt man nun die untere blaue Sekante (siehe Bild) gegen die obere laufen, geht der rote Kreis in einen Kreis über, der die beiden gegebenen Kreise berührt. Der Mittelpunkt des Berührkreises ist der Schnittpunkt der Geraden . Die Sekanten gehen in die Tangenten in den Berührpunkten über. Die Tangenten schneiden sich auf der Potenzgerade (im Bild gelb).
Entsprechende Überlegungen führen zu dem zweiten Berührkreis durch die Punkte (siehe Bild).
Durch Variation der Sekante erhält man alle Berührkreise zu den gegebenen Kreisen.
- Lage der Mittelpunkte

Ist der Mittelpunkt und der Radius des Berührkreises durch so gilt:
Die Mittelpunkte liegen also auf einer Hyperbel mit den
- Brennpunkten ,
- dem Abstand der Scheitel ,
- dem Mittelpunkt von als Mittelpunkt ,
- der linearen Exzentrizität und
- .
Überlegungen für die Mittelpunkte der Kreise, die die gegebenen Kreise umhüllen, liefern ein analoges Resultat:
Ist der Mittelpunkt und der Radius des Berührkreises durch so gilt:
Die Mittelpunkte liegen auf derselben Hyperbel wie vorher. Allerdings auf dem rechten Ast.
Siehe hierzu auch den Artikel apollonisches Problem: Lösungsmethoden.
Potenz bezüglich einer Kugel
[Bearbeiten | Quelltext bearbeiten]
Das Konzept der Potenz eines Punktes bezüglich eines Kreises lässt sich auf Kugeln im Raum übertragen.[10] Auch die Sekanten/Sehnen-Sätze haben im Raum ihre Gültigkeit. Der Beweis für den Kreisfall kann wörtlich auf den Kugelfall übertragen werden. Analog zur Potenzgerade zweier Kreise gibt es im Raum eine Potenzebene zu zwei Kugeln. Zu drei Kugeln gibt es eine dem Radikal dreier Kreise entsprechende Potenzgerade.
Literatur
[Bearbeiten | Quelltext bearbeiten]- ↑ Jakob Steiner: Einige geometrische Betrachtungen, 1826, S. 164
- ↑ Steiner, S. 163
- ↑ Steiner, S. 178
- ↑ Steiner, S. 182
- ↑ Steiner, S. 182
- ↑ Steiner: S. 170f.
- ↑ Steiner: S. 175
- ↑ Michel Chasles, C. H. Schnuse: Die Grundlehren der neuern Geometrie, erster Theil, Verlag Leibrock, Braunschweig, 1856, S. 312
- ↑ William J. M'Clelland: A Treatise on the Geometry of the Circle and Some Extensions to Conic Sections by the Method of Reciprocation, 1891, Verlag: Creative Media Partners, LLC, ISBN 978-0-344-90374-8, S. 121,220
- ↑ K.P. Grothemeyer: Analytische Geometrie, Sammlung Göschen 65/65A, Berlin 1962, S. 54
- W. Brennecke: Berührungsaufgabe für Kreis und Kugel, Verlag T. C. F. Enslin, Berlin, 1853
- Heinrich Cranz: Das apollonische Berührungsproblem, Verlag Vangerow, Bremerhaven, 1890
- Jakob Steiner: Einige geometrische Betrachtungen. In: Journal für die reine und angewandte Mathematik, Band 1, 1826, S. 161–184
- Jacob Steiner, C.F. Geiser, H. Schröter: Jacob Steiner’s Vorlesungen über synthetische Geometrie. Erster Theil: Die Theorie der Kegelschnitte in elementarer Darstellung. Teubner, 1867, S. 1–3 (books.google.com).
- Jakob Steiner: Einige geometrische Betrachtungen. In: Rudolf Sturm (Hrsg.): Ostwalds Klassiker der exakten Wissenschaften. Engelmann, Leipzig 1826, S. 15 (archive.org [abgerufen am 4. November 2024]).
- Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 28–34
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Florian Modler: Exkurs: Potenz eines Kreises auf matheplanet.de
- Eric W. Weisstein: Circle Power. In: MathWorld (englisch).
- Jacob Steiner and the Power of a Point at Convergence



































































































