Besselsche Differentialgleichung

Die Besselsche Differentialgleichung ist eine lineare gewöhnliche Differentialgleichung zweiter Ordnung. Benannt wurde sie nach dem Mathematiker Friedrich Wilhelm Bessel. Ihre Lösungen heißen Bessel-Funktionen oder Zylinderfunktionen.

Besselsche Differentialgleichung

Der Bessel-Operator ist ein Differentialoperator zweiter Ordnung, der durch

$B_n := x^2 \frac{d^2}{dx^2} + x \frac{d}{dx} + (x^2 - n^2)\, ,$

definiert ist, wobei n eine reelle oder komplexe Zahl ist.

Die Besselsche Differentialgleichung ist entsprechend eine gewöhnliche lineare Differentialgleichung zweiter Ordnung, die durch

B_nf = 0

beziehungsweise nach Ausschreiben des Bessel-Operators durch

$x^2 \frac{d^2 f}{dx^2} + x \frac{d f}{dx} + (x^2 - n^2)f = 0$

definiert ist. Die Lösungen heißen Bessel-Funktionen n-ter Ordnung.

Bessel-Funktionen

Allgemein

Die Bessel-Funktionen erster Gattung für J₀, J₁ und J₂

Die Bessel-Funktionen zweiter Gattung Y₀, Y₁ und Y₂

Die Lösungen der Besselschen Differentialgleichung heißen Bessel-Funktionen. Sie spielen eine wichtige Rolle in der Physik, da die Besselsche Differentialgleichung den radialen Anteil der Laplace-Gleichung bei zylindrischer Symmetrie darstellt. Auf die Bessel-Funktionen trifft man unter anderem bei der Untersuchung von Eigenschwingungen einer kreisförmigen Membran oder Orgelpfeife, der Ausbreitung von Wasserwellen in runden Behältern, der Wärmeleitung in Stäben, der Analyse des Frequenzspektrums von frequenzmodulierten Signalen, der Feldverteilung im Querschnitt von Rundhohlleitern, den stationären Zuständen von Kastenpotentialen und der Intensität von Lichtbeugung an kreisförmigen Löchern. Man zählt die Bessel-Funktionen wegen ihrer vielfältigen Anwendungen in der mathematischen Physik zu den speziellen Funktionen.

Als Differentialgleichung zweiter Ordnung, muss die Besselsche Differentialgleichung zwei linear unabhängige Lösungen besitzen. Es gibt jedoch verschiedene Varianten der Besselfunktionen.

Bessel-Funktionen erster Gattung J_n

Die Bessel-Funktionen erster Gattung J_n sind definiert als

$J_n(x) = \sum_{r=0}^\infty \frac{(-1)^r (\frac{x}{2})^{2r+n}}{\Gamma(n+r+1)r!} \,$ ,

wobei Γ(x) die Gammafunktion ist. Im Ursprung (x = 0) sind diese Funktionen für ganzzahlige n endlich.

Für nicht-ganzzahlige n sind J_n und J _{− n} linear unabhängige Lösungen. Für ganzzahlige n gilt jedoch die Beziehung

$J_{-n}(x)=(-1)^n J_n(x)\,$.

In diesem Fall kann die zweite unabhängige Lösung mithilfe der Bessel-Funktion zweiter Gattung gefunden werden, die weiter unten diskutiert wird.

Integraldarstellungen

Für ganzzahlige n kann man die Bessel-Funktion erster Gattung auch als Integral darstellen

$\begin{align} J_n (x) &= \frac{1}{\pi} \int_0^\pi \cos (n \tau - x \sin \tau) \,\mathrm{d}\tau\\ J_n (x) &= \frac{1}{2 \pi} \int_{-\pi}^\pi e^{-\mathrm{i}\,(n \tau - x \sin \tau)} \,\mathrm{d}\tau. \end{align}$

Hypergeometrische Funktion

Die Bessel-Funktion erster Gattung kann durch die hypergeometrische Funktion ausgedrückt werden:

$J_n(x)=\frac{(x/2)^n}{\Gamma(n+1)} \;_0F_1 (n+1; -x^2/4).$

Dieser Ausdruck hängt mit der Entwicklung der Bessel-Funktion in Abhängigkeit zur Bessel-Clifford-Funktion zusammen.

Bessel-Funktionen zweiter Gattung Y_n

Auch die Bessel-Funktionen zweiter Gattung Y_n(x) (auch Weber-Funktionen oder Neumann-Funktionen genannt) lösen die Besselsche Differentialgleichung. . Für nicht-ganzzahlige n kann man die Y_n(x) definieren durch

$Y_n(x) = \frac{J_n(x) \cos(n\pi) - J_{-n}(x)}{\sin(n\pi)}.$

Für ganzzahlige n muss man den Grenzübergang bilden

$Y_n(x) = \lim_{\alpha\to n} Y_\alpha(x).$

Nach Ausführung des Grenzüberganges mit der Regel von L’Hospital findet man, dass diese Funktionen eine logarithmische Singularität im Ursprung haben:

$\begin{align} Y_n(x) =\,& \frac2{\pi}\left(\gamma+\log\frac{x}2\right)J_n(x) - \frac1{\pi}\sum_{k=0}^{n-1}\frac{(n-k-1)!}{k!}\left(\frac{x}2\right)^{2k-n}\\ &{}- \frac1{\pi}\sum_{k=0}^{\infty}(-1)^k\frac{H_k+H_{k+n}}{k!(n+k)!}\left(\frac{x}2\right)^{2k+n} \end{align}$

Hierbei ist γ die Eulersche Konstante und H_n die harmonische Reihe.

Für alle n ist neben der Bessel-Funktion erster Gattung J_n die Bessel-Funktion zweiter Gattung Y_n eine zweite, linear unabhängige Lösung.

Für ganzzahlige n gilt wie für die Bessel-Funktionen erster Gattung die folgende Beziehung

$Y_{-n}(x) = (-1)^n Y_n(x).\,$

Bessel-Funktionen dritter Gattung H_n⁽¹⁾, H_n⁽²⁾

Die Bessel-Funktionen dritter Gattung $H_n^{(1)}$, $H_n^{(2)}$ (auch bekannt als Hankel-Funktionen) sind Linearkombinationen der Bessel-Funktionen erster und zweiter Gattung

$\begin{align} H_\alpha^{(1)}(x) &= J_\alpha(x) + i Y_\alpha(x)\,,\\ H_\alpha^{(2)}(x) &= J_\alpha(x) - i Y_\alpha(x)\,, \end{align}$

wobei i die imaginäre Einheit bezeichnet. Auch diese beiden Funktionen sind linear unabhängige Lösungen der Besselschen Differentialgleichung.

Weitere Eigenschaften

• Für die Bessel-Funktionen J_n, Y_n, $H_n^{(1)}$ und $H_n^{(2)}$ gelten die Rekursionsbeziehungen:

$\frac{n}{x} \Omega_n = \frac{1}{2}(\Omega_{n-1} + \Omega_{n+1}) \,$,

$\Omega'_n = \frac{1}{2}(\Omega_{n-1} - \Omega_{n+1}) \,$.

• Für alle $x \in \R$ gilt $\sum_{n=-\infty}^\infty J_n(x)^2 = 1$.

• Für alle $n \in \N$ gilt $\left(-\frac{1}{x}\frac{{\rm d}}{{\rm d}x}\right)^n J_0(x) = \frac{J_n(x)}{x^n}$.

Asymptotisches Verhalten

Wir nehmen für die folgende Ausdrücke an, dass n reell und nicht-negativ ist. Für kleine Argumente $0 < x \ll \sqrt{n+1}$ gelten die asymptotischen Darstellungen

$\begin{align} J_n(x) &\approx \frac{1}{\Gamma(n+1)}\left(\frac{x}{2}\right)^n \\ Y_n(x) &\approx \begin{cases} \frac{2}{\pi} \left( \ln \left(\frac{x}{2}\right) + \gamma \right) & \text{wenn } n=0 \\ \\ -\frac{\Gamma(n)}{\pi} \left( \frac{2}{x} \right)^n & \text{wenn } n > 0. \end{cases} \end{align}$

Für große Argumente $x\gg|\alpha^2 - 1/4|$ findet man

$\begin{align} J_n(x) &\approx \sqrt{\frac{2}{\pi x}} \cos \left( x-\frac{n\pi}{2} - \frac{\pi}{4} \right) \\ Y_n(x) &\approx \sqrt{\frac{2}{\pi x}} \sin \left( x-\frac{n\pi}{2} - \frac{\pi}{4} \right). \end{align}$

Diese Formeln sind für n = 1 / 2 exakt. Vergleiche hierfür mit den sphärischen Besselfunktionen weiter unten.

Modifizierte Bessel-Funktionen

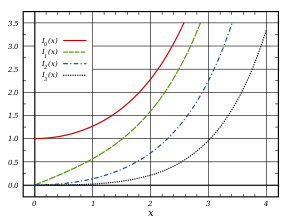
Die modifizierte Bessel-Funktionen erster Gattung für I₀, I₁, I₂ und I₃

Die modifizierte Bessel-Funktionen zweiter Gattung für K₀, K₁, K₂ und K₃

Die Differentialgleichung

$x^2 y'' + x y' - (x^2 + n^2) y = 0 \,$

wird durch Bessel-Funktionen mit rein imaginären Argument gelöst. Man definiert für ihre Lösung normalerweise die modifizierten Bessel-Funktionen

$\begin{align} I_n(x) &= i^{-n} J_n(ix)=\sum_{r=0}^\infty \frac{(\frac{x}{2})^{2r+n}}{\Gamma(r+n+1)r!} \\ K_n(x) &= \frac{\pi}{2} \frac{I_{-n} (x) - I_n (x)}{\sin (n \pi)} = \frac{\pi}{2} i^{n+1} H_n^{(1)}(ix) = \frac{\pi}{2} (-i)^{n+1} H_n^{(2)}(-ix). \end{align}$

Die Funktion K_n(x) ist auch als MacDonald-Funktion bekannt. Anders als die "normalen" Besselfunktionen weisen die modifizierten Besselfunktionen kein oszillatorisches sondern ein exponentielles Verhalten auf.

Airysche Integrale

Für die Funktionen K_{1 / 3} und K_{2 / 3} kann man eine Integraldarstellung angeben

$\begin{align} K_{1/3}(x) &= \sqrt{3} \int_0^\infty \cos\left(\frac{3}{2}x\left(u + \frac{u^3}{3}\right)\right) \mathrm{d}u \\ K_{2/3}(x) &= \sqrt{3} \int_0^\infty u \sin\left(\frac{3}{2}x\left(u + \frac{u^3}{3}\right)\right) \mathrm{d}u. \end{align}$

Hypergeometrische Funktion

Auch die modifizierte Bessel-Funktion erster Gattung kann durch die hypergeometrische Funktion ausgedrückt werden:

$I_n(x)=\frac{(x/2)^n}{\Gamma(n+1)} \;_0F_1 (n+1; x^2/4).$

Asymptotisches Verhalten

Wir nehmen wieder an, dass n reell und nicht-negativ ist. Für kleine Argumente $0 < x \ll \sqrt{n+1}$ findet man

$\begin{align} I_n(x) &\approx \frac{1}{\Gamma(n+1)}\left(\frac{x}{2}\right)^n \\ K_n(x) &\approx \begin{cases} -\left( \ln \left(\frac{x}{2}\right) + \gamma \right) & \text{wenn } n=0 \\ \\ \frac{\Gamma(n)}{2} \left( \frac{2}{x} \right)^n & \text{wenn } n > 0. \end{cases} \end{align}$

Für große Argumente $x\gg|\alpha^2 - 1/4|$ erhält man

$\begin{align} I_n(x) &\approx \frac{1}{\sqrt{2\pi x}} e^x \left(1+\mathcal{O}\left(\frac{1}{x}\right)\right) \\ K_n(x) &\approx \sqrt{\frac{\pi}{2 x}} e^{-x} \left(1+\mathcal{O}\left(\frac{1}{x}\right)\right). \end{align}$

Sphärische Besselfunktionen

Die Helmholtz-Gleichung in Kugelkoordinaten führt nach Separation der Variablen auf die Radialgleichung

$x^2 \frac{d^2 f_l(x)}{dx^2} + 2x \frac{df_l(x)}{dx} + [x^2 - l(l+1)]f_l(x) = 0.$

Nach der Substitution

$u_l(x)=\frac{1}{\sqrt{x}} f_l(x)$

erhält man die Besselsche Differentialgleichung (n = l + 1 / 2)

$x^2 \frac{d^2 u_l(x)}{dx^2} + x \frac{du_l(x)}{dx} + \left[x^2 - \left(l+\frac{1}{2}\right)^2\right]u_l(x) = 0.$

Für die Lösung f_l(x) der Radialgleichung werden üblicherweise die sphärischen Bessel-Funktionen j_l(x), die sphärischen Neumann-Funktionen y_l(x) und die sphärischen Hankel-Funktionen $h_l^{(1,2)}(x)$ definiert:

$\begin{align} j_l(x)&=\sqrt{\frac{\pi}{2x}} J_{l+1/2}(x) \\ y_l(x)&=\sqrt{\frac{\pi}{2x}} Y_{l+1/2}(x) \\ h_l^{(1,2)}(x)&=\sqrt{\frac{\pi}{2x}} H_{l+1/2}^{(1,2)} = j_l(x)\pm i y_l(x)\\ \end{align}$.

Sowohl j_l(x) und y_l(x) als auch $h_l^{(1,2)}(x)$ sind linear unabhängige Lösungen.

Es gelten die alternativen Darstellungen

$\begin{align}j_l(x) &= (-x)^l \left(\frac{1}{x}\frac\mathrm{d}{\mathrm{d}x}\right)^l \ \frac{\sin x}{x}\\ y_l(x) &= -(-x)^l \left(\frac{1}{x}\frac\mathrm{d}{\mathrm{d}x}\right)^l \ \frac{\cos x}{x} \\ h_l^{(1,2)} (x) &= \mp i (-x)^l \left(\frac{1}{x} \frac\mathrm{d}{\mathrm{d}x}\right)^l \frac{e^{\pm i x}}{x}\\ \end{align}$

Die sphärischen Bessel- und Hankelfunktionen werden beispielsweise für die Behandlung des kugelsymmetrischen Potentialtopfs in der Quantenmechanik benötigt.

Weitere Eigenschaften

• Für die sphärischen Bessel-Funktionen j_n, y_n, $h_n^{(1)}$ und $h_n^{(2)}$ gelten die Rekursionsbeziehungen:

$\begin{align} \frac{2l+1}{x} \omega_l(x) &= \omega_{l-1}(x) + \omega_{l+1}(x) \\ \omega'_l(x) &= \frac{1}{2l+1}\left(l\omega_{l-1}(x)-(l+1)\omega_{l+1}(x)\right) \\ \frac{\mathrm{d}}{\mathrm{d}x}(x \omega_l(x)) &= x\omega_{l-1}(x) - l \omega_l(x). \end{align}$.

• Für die Wronski-Determinante gilt

$W(j_l, y_n) = \frac{1}{i} W(j_l,h_l^{(1)}) = - W(y_l, h_l^{(1)}) = \frac{1}{x^2}$

Hankel-Transformation

→ Hauptartikel: Hankel-Transformation

Die Hankel-Transformation ist eine Integraltransformation, die eng mit der Fourier-Transformation verwandt ist. Der Integralkern der Hankel-Transformation ist die Bessel-Funktion erster Gattung J_n, das heißt der Integraloperator lautet

$H_n(f)(s) = \int_0^\infty J_n(t s) t f(t) \mathrm{d} t\,.$

Eine besondere Eigenschaft der Hankel-Transformation ist, dass mit ihr der Bessel-Operator in einen algebraischen Ausdruck (eine Multiplikation) überführt werden kann.

Literatur

• Milton Abramowitz, Irene Stegun: Handbook of Mathematical Functions. Dover, New York 1972, S. 355.
• Paul Schafheitlin Die Theorie der Besselschen Funktionen. B. G. Teubner, Leipzig 1908.
• J. H. Graf, E. Gubler: Einleitung in die Theorie der Bessel'schen Funktionen. Erster Band Zweiter Band. K. J. Wyss, Bern 1900
• John David Jackson: Classical Electrodynamics. John Wiley, New York NY 1962 (3. edition. ebenda 1999, ISBN 0-471-30932-X; deutsch: 4. überarbeitete Auflage. de Gruyter, Berlin u. a. 2006, ISBN 3-11-018970-4).
• Carl Neumann: Theorie der Besselschen Funktionen, ein Analogon zur Theorie der Kugelfunktionen. B. G. Teubner, Leipzig 1867.
• Wolfgang Nolting: Grundkurs Theoretische Physik 5/2. Quantenmechanik - Methoden und Anwendungen, 6. Auflage, Springer-Lehrbuch, 2006, ISBN 978-3-540-26035-6

Weblinks

• Eric W. Weisstein: Bessel Differential Equation. In: MathWorld. (englisch)
• Besselfunktionen ν-ter Ordnung mit reellem Argument – Javascript