Fehlerfunktion

Als Fehlerfunktion oder Gaußsche Fehlerfunktion bezeichnet man in der Theorie der speziellen Funktionen die durch das Integral
definierte Funktion.[1] Damit ist die Fehlerfunktion eine Stammfunktion von , und zwar die einzige ungerade (gerade Funktionen mit Stammfunktion besitzen genau eine ungerade solche).
Für ein reelles Argument ist eine reellwertige Funktion; zur Verallgemeinerung auf komplexe Argumente siehe unten.
Die Fehlerfunktion ist eine Sigmoidfunktion, findet Anwendung in der Statistik und in der Theorie der partiellen Differentialgleichungen und hängt eng mit dem Fehlerintegral zusammen.
Bezeichnungen[Bearbeiten | Quelltext bearbeiten]
Die Bezeichnung kommt von error function.
Komplementäre Fehlerfunktion[Bearbeiten | Quelltext bearbeiten]
Die komplementäre (bzw. konjugierte) Fehlerfunktion ist gegeben durch:
Verallgemeinerte Fehlerfunktion[Bearbeiten | Quelltext bearbeiten]
Die verallgemeinerte Fehlerfunktion wird durch das Integral
definiert.
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Es gilt:
Die Fehlerfunktion ist ungerade:
Das uneigentliche Integral von bis ist
Außerdem gilt:
Verwendung[Bearbeiten | Quelltext bearbeiten]
Verwandtschaft mit der Normalverteilung[Bearbeiten | Quelltext bearbeiten]
Die Fehlerfunktion hat eine gewisse Ähnlichkeit mit der Verteilungsfunktion der Normalverteilung. Sie hat jedoch eine Zielmenge von , während eine Verteilungsfunktion zwingend Werte aus dem Bereich annehmen muss.
Es gilt für die Standardnormalverteilung
bzw. für die Verteilungsfunktion einer beliebigen Normalverteilung mit Standardabweichung und Erwartungswert
Falls die Abweichungen der einzelnen Ergebnisse einer Messreihe vom gemeinsamen Mittelwert durch eine Normalverteilung mit Standardabweichung und Erwartungswert 0 beschrieben werden können, dann ist die Wahrscheinlichkeit, mit der der Messfehler einer einzelnen Messung zwischen und liegt (für positives ).
Die Fehlerfunktion kann verwendet werden, um mit Hilfe der Inversionsmethode normalverteilte Pseudozufallszahlen zu generieren.[2]
Wärmeleitungsgleichung[Bearbeiten | Quelltext bearbeiten]
Die Fehlerfunktion und die komplementäre Fehlerfunktion kommen beispielsweise in Lösungen der Wärmeleitungsgleichung vor, wenn Randwertbedingungen durch die Heaviside-Funktion vorgegeben sind.
Numerische Berechnung[Bearbeiten | Quelltext bearbeiten]
Die Fehlerfunktion ist wie die Verteilungsfunktion der Normalverteilung nicht durch eine geschlossene Funktion darstellbar und muss numerisch bestimmt werden.
Für kleine reelle Werte erfolgt die Berechnung mit der Reihenentwicklung
für große reelle Werte mit der Kettenbruchentwicklung
Für den kompletten Wertebereich gibt es folgende Approximation mit einem maximalen Fehler von :[3]
mit
und
Eine für alle reellen Werte von schnell konvergierende Entwicklung[4] erhält man unter Verwendung des Theorems von Heinrich H. Bürmann:[5][6]
Durch geeignete Wahl von und ergibt sich daraus eine Näherung, deren größter relativer Fehler bei kleiner als ist:
Wertetabelle[Bearbeiten | Quelltext bearbeiten]
| 0,00 | 0,0000000 | 1,0000000 | 1,30 | 0,9340079 | 0,0659921 | |
| 0,05 | 0,0563720 | 0,9436280 | 1,40 | 0,9522851 | 0,0477149 | |
| 0,10 | 0,1124629 | 0,8875371 | 1,50 | 0,9661051 | 0,0338949 | |
| 0,15 | 0,1679960 | 0,8320040 | 1,60 | 0,9763484 | 0,0236516 | |
| 0,20 | 0,2227026 | 0,7772974 | 1,70 | 0,9837905 | 0,0162095 | |
| 0,25 | 0,2763264 | 0,7236736 | 1,80 | 0,9890905 | 0,0109095 | |
| 0,30 | 0,3286268 | 0,6713732 | 1,90 | 0,9927904 | 0,0072096 | |
| 0,35 | 0,3793821 | 0,6206179 | 2,00 | 0,9953223 | 0,0046777 | |
| 0,40 | 0,4283924 | 0,5716076 | 2,10 | 0,9970205 | 0,0029795 | |
| 0,45 | 0,4754817 | 0,5245183 | 2,20 | 0,9981372 | 0,0018628 | |
| 0,50 | 0,5204999 | 0,4795001 | 2,30 | 0,9988568 | 0,0011432 | |
| 0,55 | 0,5633234 | 0,4366766 | 2,40 | 0,9993115 | 0,0006885 | |
| 0,60 | 0,6038561 | 0,3961439 | 2,50 | 0,9995930 | 0,0004070 | |
| 0,65 | 0,6420293 | 0,3579707 | 2,60 | 0,9997640 | 0,0002360 | |
| 0,70 | 0,6778012 | 0,3221988 | 2,70 | 0,9998657 | 0,0001343 | |
| 0,75 | 0,7111556 | 0,2888444 | 2,80 | 0,9999250 | 0,0000750 | |
| 0,80 | 0,7421010 | 0,2578990 | 2,90 | 0,9999589 | 0,0000411 | |
| 0,85 | 0,7706681 | 0,2293319 | 3,00 | 0,9999779 | 0,0000221 | |
| 0,90 | 0,7969082 | 0,2030918 | 3,10 | 0,9999884 | 0,0000116 | |
| 0,95 | 0,8208908 | 0,1791092 | 3,20 | 0,9999940 | 0,0000060 | |
| 1,00 | 0,8427008 | 0,1572992 | 3,30 | 0,9999969 | 0,0000031 | |
| 1,10 | 0,8802051 | 0,1197949 | 3,40 | 0,9999985 | 0,0000015 | |
| 1,20 | 0,9103140 | 0,0896860 | 3,50 | 0,9999993 | 0,0000007 |
Komplexe Fehlerfunktion[Bearbeiten | Quelltext bearbeiten]
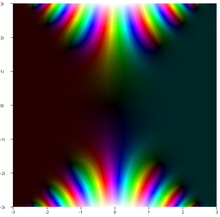
Die Definitionsgleichung der Fehlerfunktion kann auf komplexe Argumente ausgeweitet werden:
In diesem Fall ist eine komplexwertige Funktion. Unter komplexer Konjugation gilt
- .
Imaginäre Fehlerfunktion[Bearbeiten | Quelltext bearbeiten]
Die imaginäre Fehlerfunktion ist gegeben durch
mit der Reihenentwicklung
- .
Zur Berechnung können und weitere verwandte Funktionen auch durch die Faddeeva-Funktion ausgedrückt werden. Die Faddeeva-Funktion ist eine skalierte komplexe komplementäre Fehlerfunktion und auch als relativistische Plasma-Dispersions-Funktion bekannt. Sie ist mit den Dawson-Integralen und dem Voigt-Profil verwandt. Eine numerische Implementierung von Steven G. Johnson steht als C-Bibliothek libcerf zur Verfügung.[7]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Milton Abramowitz, Irene A. Stegun (Hrsg.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York 1972, Chapter 7.
- William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery: Numerical Recipes in C. 2. Auflage. Cambridge 1992, S. 220 ff. (PDF; 76 kB)
- Bronstein, I.N. und Semendjajew, K.A., Taschenbuch der Mathematik, 6. Auflage, Verlag Harri Deutsch, Frankfurt am Main 2005, S. 782
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Bronstein, Semendjajew, Taschenbuch der Mathematik, 6. Auflage, S. 782
- ↑ Für eine konkrete Implementierung siehe z. B. Peter John Acklam: An algorithm for computing the inverse normal cumulative distribution function. ( vom 5. Mai 2007 im Internet Archive)
- ↑ Numerical Recipes in Fortran 77: The Art of Scientific Computing. Cambridge University Press, 1992, ISBN 0-521-43064-X, S. 214.
- ↑ H. M. Schöpf, P. H. Supancic: On Bürmann’s Theorem and Its Application to Problems of Linear and Nonlinear Heat Transfer and Diffusion. In: The Mathematica Journal, 2014. doi:10.3888/tmj.16-11.
- ↑ Moritz Cantor: Bürmann, Heinrich. In: Allgemeine Deutsche Biographie (ADB). Band 47, Duncker & Humblot, Leipzig 1903, S. 392–394.
- ↑ E. W. Weisstein: Bürmann’s Theorem. mathworld
- ↑ Steven G. Johnson, Joachim Wuttke: libcerf.














![{\displaystyle \operatorname {erf} (x)^{2}={\frac {4}{\pi }}\int _{0}^{1}{\frac {1-\exp[-x^{2}(y^{2}+1)]}{y^{2}+1}}\mathrm {d} y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12945ca7903dbb5803328b1c5139cabfc79d9ed4)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
































