Verteilungsfunktion
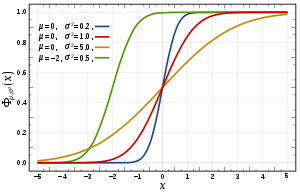
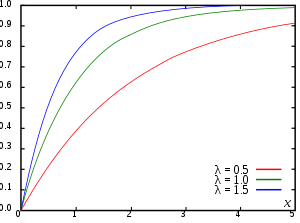
Die Verteilungsfunktion ist eine spezielle reelle Funktion in der Stochastik und ein zentrales Konzept bei der Untersuchung von Wahrscheinlichkeitsverteilungen auf den reellen Zahlen. Jeder Wahrscheinlichkeitsverteilung und jeder reellwertigen Zufallsvariable kann eine Verteilungsfunktion zugeordnet werden. Anschaulich entspricht dabei der Wert der Verteilungsfunktion an der Stelle der Wahrscheinlichkeit, dass die zugehörige Zufallsvariable einen Wert kleiner oder gleich annimmt. Ist beispielsweise die Verteilung der Schuhgrößen in Europa gegeben, so entspricht der Wert der entsprechenden Verteilungsfunktion bei 45 der Wahrscheinlichkeit, dass ein beliebiger Europäer die Schuhgröße 45 oder kleiner besitzt.
Ihre Bedeutung erhält die Verteilungsfunktion durch den Korrespondenzsatz, der besagt, dass jeder Verteilungsfunktion eine Wahrscheinlichkeitsverteilung auf den reellen Zahlen zugeordnet werden kann und umgekehrt. Die Zuordnung ist bijektiv. Dies ermöglicht es, anstelle der Untersuchung von Wahrscheinlichkeitsverteilungen als Mengenfunktionen auf einem komplexen Mengensystem mit Methoden der Maßtheorie die entsprechenden Verteilungsfunktionen zu untersuchen. Diese sind reelle Funktionen und somit über die Methoden der reellen Analysis leichter zugänglich.
Als alternative Bezeichnungen finden sich unter anderem kumulierte Verteilungsfunktion bzw. kumulative Verteilungsfunktion, da sie die Wahrscheinlichkeiten, kleiner als zu sein, anhäuft (siehe auch kumulierte Häufigkeit). Weiterhin wird sie zur besseren Abgrenzung von ihrem höherdimensionalen Pendant, der multivariaten Verteilungsfunktion, auch als univariate Verteilungsfunktion bezeichnet.[1] In Abgrenzung zum allgemeineren maßtheoretischen Konzept einer Verteilungsfunktion finden sich die Bezeichnungen als wahrscheinlichkeitstheoretische Verteilungsfunktion oder als Verteilungsfunktion im engeren Sinn.[2]
Die Entsprechung der Verteilungsfunktion in der deskriptiven Statistik ist die empirische Verteilungs- oder Summenhäufigkeitsfunktion.
Definition[Bearbeiten | Quelltext bearbeiten]
Definition mittels Wahrscheinlichkeitsmaß[Bearbeiten | Quelltext bearbeiten]
Gegeben sei ein Wahrscheinlichkeitsmaß auf dem Ereignisraum der reellen Zahlen, d. h., jede reelle Zahl kann als mögliches Ergebnis aufgefasst werden. Dann heißt die Funktion
definiert durch:
die Verteilungsfunktion von . Mit anderen Worten: Die Funktion gibt an der Stelle an, mit welcher Wahrscheinlichkeit ein Ergebnis aus der Menge (alle reellen Zahlen kleiner oder gleich ) eintritt.
Definition mittels Zufallsvariable[Bearbeiten | Quelltext bearbeiten]
Ist eine reelle Zufallsvariable, so nennt man die Funktion
die Verteilungsfunktion von . Dabei bezeichnet die Wahrscheinlichkeit, dass einen Wert kleiner oder gleich annimmt.
Somit ist die Verteilungsfunktion einer Zufallsvariablen genau die Verteilungsfunktion ihrer Verteilung.
Beispiele[Bearbeiten | Quelltext bearbeiten]
Wahrscheinlichkeitsmaße mit Dichten[Bearbeiten | Quelltext bearbeiten]
Besitzt das Wahrscheinlichkeitsmaß eine Wahrscheinlichkeitsdichte , so gilt
- .
Somit hat in diesem Fall die Verteilungsfunktion die Darstellung
- .
Beispielsweise hat die Exponentialverteilung die Dichte
- .
Ist also die Zufallsvariable exponentialverteilt, also , so ist
- .
Dieses Vorgehen ist jedoch nicht allgemein gangbar. Erstens besitzen nicht alle Wahrscheinlichkeitsmaße auf den reellen Zahlen eine Dichtefunktion (beispielsweise diskrete Verteilungen, aufgefasst als Verteilungen in ); zweitens muss selbst bei der Existenz einer Dichtefunktion nicht notwendigerweise eine Stammfunktion mit geschlossener Darstellung existieren (so beispielsweise bei der Normalverteilung).
Diskrete Wahrscheinlichkeitsmaße[Bearbeiten | Quelltext bearbeiten]
Betrachtet man zu einem Parameter eine Bernoulli-verteilte Zufallsvariable , so ist
und für die Verteilungsfunktion folgt dann
Ist allgemeiner eine Zufallsvariable mit Werten in den nichtnegativen ganzen Zahlen , dann gilt
- .
Dabei bezeichnet die Abrundungsfunktion, das heißt ist größte ganze Zahl, die kleiner oder gleich ist.
Eigenschaften und Zusammenhang zur Verteilung[Bearbeiten | Quelltext bearbeiten]
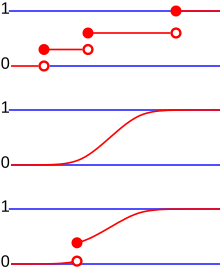
Jede Verteilungsfunktion hat folgende Eigenschaften:
- ist monoton steigend.
- ist rechtsseitig stetig.
- und .
Darüber hinaus ist jede Funktion , die die Eigenschaften 1, 2 und 3 erfüllt, eine Verteilungsfunktion. Folglich ist eine Charakterisierung der Verteilungsfunktion mit Hilfe der drei Eigenschaften möglich. So gibt es zu jeder Verteilungsfunktion genau solch ein Wahrscheinlichkeitsmaß , dass für alle gilt:
Umgekehrt gibt es zu jedem Wahrscheinlichkeitsmaß eine Verteilungsfunktion derart, dass für alle gilt:
Daraus folgt die Korrespondenz von und . Dieser Sachverhalt wird in der Literatur auch Korrespondenzsatz genannt.[3]
Jede Verteilungsfunktion besitzt höchstens abzählbar viele Sprungstellen.
Da jede Verteilungsfunktion rechtsstetig ist, existiert auch der rechtsseitige Grenzwert und es gilt für alle :
Deswegen ist genau dann stetig, wenn für alle gilt.
Rechnen mit Verteilungsfunktionen[Bearbeiten | Quelltext bearbeiten]
Ist eine Verteilungsfunktion gegeben, so kann man wie folgt die Wahrscheinlichkeiten bestimmen:
- sowie bzw.
- sowie .
Daraus folgt dann auch
- und
für .
Im Allgemeinen kann hier die Art der Ungleichheitszeichen ( oder ) beziehungsweise die Art der Intervallgrenzen (offen, abgeschlossen, links/rechts halboffen) nicht vernachlässigt werden. Dies führt bei diskreten Wahrscheinlichkeitsverteilungen zu Fehlern, da sich dort auch auf einzelnen Punkten eine Wahrscheinlichkeit befinden kann, die dann fälschlicherweise dazugezählt oder nicht berücksichtigt wird.
Bei stetigen Wahrscheinlichkeitsverteilungen, also insbesondere auch bei solchen, die über eine Wahrscheinlichkeitsdichtefunktion definiert werden (Absolutstetige Wahrscheinlichkeitsverteilungen), führt eine Abänderung der Ungleichheitszeichen oder Intervallgrenzen nicht zu Fehlern.
- Beispiel
Beim Würfeln errechnet sich die Wahrscheinlichkeit, eine Zahl zwischen 2 (exklusive) und einschließlich 5 zu würfeln, zu
- .
Konvergenz[Bearbeiten | Quelltext bearbeiten]
Definition[Bearbeiten | Quelltext bearbeiten]
Eine Folge von Verteilungsfunktionen heißt schwach konvergent gegen die Verteilungsfunktion , wenn
- gilt für alle , an denen stetig ist.[4]
Für Verteilungsfunktionen von Zufallsvariablen finden sich auch die Bezeichnungen konvergent in Verteilung oder stochastisch konvergent.[5]
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Über die schwache Konvergenz der Verteilungsfunktionen lässt sich mit dem Satz von Helly-Bray eine Brücke zur schwachen Konvergenz von Maßen schlagen. Denn eine Folge von Wahrscheinlichkeitsmaßen ist genau dann schwach konvergent, wenn die Folge ihrer Verteilungsfunktionen schwach konvergiert. Analog ist eine Folge von Zufallsvariablen genau denn Konvergent in Verteilung, wenn die Folge ihrer Verteilungsfunktionen schwach konvergiert.
Einige Autoren nutzen diese Äquivalenz zur Definition der Konvergenz in Verteilung, da sie leichter zugänglich ist als die schwache Konvergenz der Wahrscheinlichkeitsmaße. Teilweise findet sich die Aussage des Satzes von Helly-Bray auch im Portmanteau-Theorem.
Für Verteilungsfunktionen im Sinne der Maßtheorie ist die oben angegebene Definition nicht korrekt, sondern entspricht der vagen Konvergenz von Verteilungsfunktionen (im Sinne der Maßtheorie). Diese fällt aber für Wahrscheinlichkeitsmaßen mit der schwachen Konvergenz von Verteilungsfunktionen zusammen. Die schwache Konvergenz von Verteilungsfunktionen wird von dem Lévy-Abstand metrisiert.
Klassifikation von Wahrscheinlichkeitsverteilungen über Verteilungsfunktionen[Bearbeiten | Quelltext bearbeiten]
Wahrscheinlichkeitsverteilungen, deren Verteilungsfunktion stetig ist, werden stetige Wahrscheinlichkeitsverteilungen genannt. Sie lassen sich noch weiter unterteilen in
- Absolutstetige Wahrscheinlichkeitsverteilungen, für die eine Wahrscheinlichkeitsdichtefunktion existiert. Typische Beispiele hierfür wäre die Normalverteilung oder die Exponentialverteilung.
- Stetigsinguläre Wahrscheinlichkeitsverteilungen, die keine Wahrscheinlichkeitsdichtefunktion besitzen. Beispiel hierfür wäre die Cantor-Verteilung.
Für absolutstetige Wahrscheinlichkeitsverteilungen entspricht die Ableitung der Verteilungsfunktion der Wahrscheinlichkeitsdichtefunktion. Zwar sind auch stetigsinguläre Wahrscheinlichkeitsverteilungen fast überall differenzierbar, ihre Ableitung ist aber fast überall gleich null.
Verteilungsfunktionen von diskreten Wahrscheinlichkeitsverteilungen zeichnen sich durch ihre Sprünge zwischen den Bereichen mit konstanten Funktionswerten aus. Bei ihnen handelt es sich um Sprungfunktionen.
Alternative Definition[Bearbeiten | Quelltext bearbeiten]
Linksseitig stetige Verteilungsfunktionen[Bearbeiten | Quelltext bearbeiten]
Im Einflussbereich der Tradition Kolmogorows, namentlich der mathematischen Literatur des ehem. „Ostblocks“, findet sich parallel zur heute vorherrschenden „Kleiner-gleich“-Konvention der Verteilungsfunktion bis in die jüngere Vergangenheit eine weitere, die statt des Kleiner-gleich-Zeichens das Echt-kleiner-Zeichen verwendet,[6][7] also
Bei stetigen Wahrscheinlichkeitsverteilungen stimmen beide Definitionen überein, bei diskreten Verteilungen dagegen unterscheiden sie sich darin, dass die Verteilungsfunktion im Fall der „Echt-kleiner“-Konvention an den Sprungstellen nicht rechtsseitig, sondern linksseitig stetig ist.
Beispiel[Bearbeiten | Quelltext bearbeiten]
Es ergibt sich beispielsweise für die Binomialverteilung bei der heute üblichen „Kleiner-gleich“-Konvention eine Verteilungsfunktion der Form
- ,
bei der „Echt-kleiner“-Konvention dagegen die Schreibweise
- .
Speziell für gilt im zweiten Fall also[8]
- .
Verwandte Konzepte[Bearbeiten | Quelltext bearbeiten]
Empirische Verteilungsfunktion[Bearbeiten | Quelltext bearbeiten]
Die empirische Verteilungsfunktion einer Stichprobe spielt eine wichtige Rolle in der Statistik. Formal entspricht sie der Verteilungsfunktion einer diskreten Gleichverteilung auf den Punkten . Ihre Bedeutung hat sie daher, dass nach dem Satz von Gliwenko-Cantelli die empirische Verteilungsfunktion einer unabhängigen Stichprobe von Zufallszahlen gegen die Verteilungsfunktion der Wahrscheinlichkeitsverteilung konvergiert, mittels der die Zufallszahlen erzeugt wurden.
Gemeinsame Verteilungsfunktion und Rand-Verteilungsfunktionen[Bearbeiten | Quelltext bearbeiten]
Die Gemeinsame Verteilungsfunktion verallgemeinert das Konzept einer Verteilungsfunktion von der Verteilung einer Zufallsvariablen auf die Gemeinsame Verteilung von Zufallsvariablen. Ebenso lässt sich das Konzept von der Randverteilung zur Rand-Verteilungsfunktion übertragen. Diese Verteilungsfunktionen haben gemeinsam, dass ihr Definitionsbereich der ist für
Verallgemeinerte Inverse Verteilungsfunktion[Bearbeiten | Quelltext bearbeiten]
Die Verallgemeinerte inverse Verteilungsfunktion bildet unter Umständen eine Umkehrfunktion zur Verteilungsfunktion und ist wichtig zur Bestimmung von Quantilen.
Verteilungsfunktion im Sinne der Maßtheorie[Bearbeiten | Quelltext bearbeiten]
Verteilungsfunktionen können nicht nur für Wahrscheinlichkeitsmaße definiert werden, sondern für beliebige endliche Maße auf den reellen Zahlen. In diesen Verteilungsfunktionen (im Sinne der Maßtheorie) spiegeln sich dann wichtige Eigenschaften der Maße wider. Sie bilden eine Verallgemeinerung der hier besprochenen Verteilungsfunktionen.
Überlebensfunktion[Bearbeiten | Quelltext bearbeiten]
Die Überlebensfunktion gibt im Gegensatz zu einer Verteilungsfunktion an, wie groß die Wahrscheinlichkeit ist, einen gewissen Wert zu Überschreiten. Sie tritt beispielsweise bei der Modellierung von Lebensdauern auf und gibt dort an, wie groß die Wahrscheinlichkeit ist, einen gewissen Zeitpunkt zu „überleben“.
Multivariate und mehrdimensionale Verteilungsfunktion[Bearbeiten | Quelltext bearbeiten]
Die Multivariate Verteilungsfunktion ist die Verteilungsfunktion, die multivariaten Wahrscheinlichkeitsverteilungen zugeordnet wird. Als mehrdimensionale Verteilungsfunktion wird hingegen meist das höherdimensionale Pendant der Verteilungsfunktion im Sinne der Maßtheorie bezeichnet.
Mischverteilung[Bearbeiten | Quelltext bearbeiten]
Eine Mischverteilung beschreibt Mischungen von Zufallsgrößen, die unterschiedlichen Verteilungen folgen.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Klaus D. Schmidt: Maß und Wahrscheinlichkeit. 2., durchgesehene Auflage. Springer-Verlag, Heidelberg / Dordrecht / London / New York 2011, ISBN 978-3-642-21025-9, doi:10.1007/978-3-642-21026-6.
- Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin / Heidelberg 2013, ISBN 978-3-642-36017-6, doi:10.1007/978-3-642-36018-3.
- Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin / Heidelberg 2014, ISBN 978-3-642-45386-1, doi:10.1007/978-3-642-45387-8.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Schmidt: Maß- und Wahrscheinlichkeit. 2011, S. 246.
- ↑ Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. 2014, S. 62.
- ↑ N. Schmitz: Vorlesungen über Wahrscheinlichkeitstheorie. Teubner, 1996.
- ↑ Schmidt: Maß- und Wahrscheinlichkeit. 2011, S. 396.
- ↑ Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. 2014, S. 287.
- ↑ Alexandr Alexejewitsch Borowkow: Rachunek prawdopodobieństwa. Państwowe Wydawnictwo Naukowe, Warszawa 1977, S. 36 ff.
- ↑ Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. VEB Deutscher Verlag der Wissenschaften, Elfte Auflage, Berlin 1989, Definition 2.2.1, S. 51.
- ↑ W. Gellert, H. Küstner, M. Hellwich, H. Kästner (Hrsg.): Kleine Enzyklopädie Mathematik. VEB Verlag Enzyklopädie Leipzig 1970, OCLC 174754758, S. 659–660.



![{\displaystyle F_{P}\colon \mathbb {R} \to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d2e428d6aaa54fa25289ec92f0fe95e8057387e)
![{\displaystyle F_{P}(x)=P((-\infty ,x])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef8e83eb5201467cbb2dcd0afe44971d70ca95a)
![{\displaystyle (-\infty ,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad2402c0ff48631309599dc5d8be7607fb994d8d)



![{\displaystyle P((a,b])=\int _{a}^{b}f_{P}(x)\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddd9cfff49a23ceb40a6bb483b3f06bd5aa24b84)












![{\displaystyle F\colon \mathbb {R} \rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4c45b6faf38bb3fb300ab4678d3675afd172f56)



![{\displaystyle P_{F}\colon {\mathcal {B}}(\mathbb {R} )\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f028a26b4d83d4e753de7e2f078ae55d55904097)

![{\displaystyle P_{F}\left(]-\infty ,x]\right)=F(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a1576e643e0cf9c3848df80fae46fac65f09378)
![{\displaystyle P\colon {\mathcal {B}}(\mathbb {R} )\to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/914424c5a0da8466438e221a5d22de2aab4ef610)
![{\displaystyle F_{P}\colon \mathbb {R} \rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8c0dd4c1038f93abe968e70d19b188b7f29332c)
![{\displaystyle P\left(]-\infty ,x]\right)=F_{P}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0405857991ccd542fbd42ff0857e57154b7a084b)






![{\displaystyle P((-\infty ;a])=F(a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c87fb872c6a3251f82fd21f908111708d1489a8)


![{\displaystyle P((a;b])=F(b)-F(a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcc1d1c84afe5749824309e68d2c1aa581dcf21d)













