Oktaedergruppe


In der Mathematik ist die Oktaedergruppe je nach Konvention
- die Symmetriegruppe eines regulären Oktaeders, also die Menge der (Kongruenz-)Abbildungen, die ein regelmäßiges Oktaeder wieder auf sich selbst, d. h. Ecken auf Ecken, Kanten auf Kanten usw., abbilden, oder
- die Drehgruppe eines Oktaeders, eine Untergruppe der Symmetriegruppe, bei der Spiegelungen und Drehspiegelungen nicht zugelassen sind.
Die volle Symmetriegruppe ist das direkte Produkt der Drehgruppe mit der zweielementigen Gruppe, die von der Punktspiegelung am Mittelpunkt erzeugt wird. Im zweiten Fall wird sie zur Unterscheidung auch vollständige, binäre oder erweiterte Oktaedergruppe genannt (nach Felix Klein).
Gemeinsam sind beiden Gruppen die folgenden Abbildungen als Elemente:
- je eine 90°-, 180°- und 270°-Drehung um die drei 4-zähligen Drehachsen (durch gegenüberliegende Ecken),
- je eine 120°- und 240°-Drehung um die vier 3-zähligen Drehachsen (durch gegenüberliegende Flächenmittelpunkte),
- je eine 180°-Drehung um die sechs 2-zähligen Drehachsen (durch gegenüberliegende Kantenmittelpunkte) und
- die Identität.
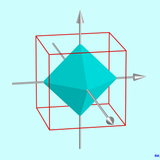
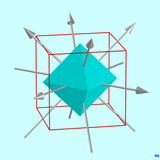
Daraus ergeben sich Elemente der Drehgruppe, kombiniert mit der Punktspiegelung ergeben sich Elemente der Symmetriegruppe. In den drei Grafiken sind alle 13 Drehachsen (Achsen der Rotationssymmetrie) dargestellt. Der zum Oktaeder duale Würfel ist als Drahtgittermodell mit eingezeichnet.
Die Gruppen für Oktaeder und Würfel sind isomorph, da duale Körper den gleichen Symmetrietyp besitzen. Daher kann man die Oktaedergruppe genauso gut auch Würfelgruppe nennen. Die Drehgruppen beider Körper sind isomorph zur symmetrischen Gruppe , nämlich zur Gruppe der Permutationen der 4 dreizähligen Drehachsen. Beim Würfel sind das die Raumdiagonalen und beim Oktaeder die Verbindungslinien gegenüberliegender Flächenmittelpunkte.
In der Kristallographie bezeichnet man die Drehgruppe des Oktaeders mit dem Schoenflies-Symbol und die volle Symmetriegruppe mit .
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- Felix Klein: Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade. Teubner, Leipzig 1884, S. 24 ff. (VIII, 260, online).
- Arthur Schoenflies: Krystallsysteme und Krystallstructur. Teubner, Leipzig 1891 (XII, 638 S., Online-Ressourcen).
- John S. Lomont: Applications of finite groups. Reprint Auflage. Dover Publications, New York 1993, ISBN 0-486-67376-6, S. 81 (XI, 346 S., Reprint der Auflage: Academic Press, New York 1959).
- Harold Scott MacDonald Coxeter: Regular polytopes. 3. ed., unabridged and corr. repr. of the 2. ed., New York, Macmillan, 1963. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 46–47 (XIII, 321 S., eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 25. Januar 2020] Die Vorschau enthält keine Seitennummerierung.).
- Frank Albert Cotton: Chemical applications of group theory. 3. ed. Wiley, New York, NY 1990, ISBN 0-471-51094-7, S. 47–49 (XIV, 461 S.).
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Octahedral Group, Mathworld
- Uni Freiburg, Spezial: Oktaeder. Abgerufen am 7. März 2020.