Polyomino

Ein Polyomino (Kunstwort, abgeleitet von Domino) ist eine Fläche, die aus $n$ zusammenhängenden Quadraten besteht. Für kleine $n$ sind auch die Bezeichnungen Triomino ($n=3$), Tetromino ($n=4$), Pentomino ($n=5$) und Hexomino ($n=6$) üblich.

Definition

Ein Polyomino oder $n$-Mino ist eine Figur $P$, die aus $n \geq 1$ kongruenten Quadraten besteht, für die gilt

1. je zwei Quadrate haben entweder keinen Punkt oder eine Ecke oder eine Kante gemeinsam,
2. zu je zwei verschiedenen Quadraten $Q_1$ und $Q^*$ aus $P$ gibt es eine Folge $Q_1 Q_2 \ldots Q_{k-1} Q^*$ von benachbarten Quadraten aus $P$.

Dabei heißen zwei Quadrate benachbart, wenn die Menge ihrer gemeinsamen Punkte eine Seite ist. Folgende Beispiele stellen demnach keine Polyominos dar.

1. gilt nicht

1. gilt nicht

2. gilt nicht

2. gilt nicht

Für besondere Anwendungen wird zusätzlich gefordert:

• $P$ bildet eine einfach zusammenhängende Punktmenge.

Polyomino mit Loch

Darstellung über Zusammenhangsgraphen

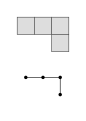
Jedem Polyomino $P$ lässt sich ein Zusammenhangsgraph zuordnen, indem man jedes Quadrat aus $P$ als Knoten und das Benachbartsein zweier Quadrate durch eine Kante wiedergibt. Nachfolgend wird dies anhand der 5 Tetrominos dargestellt.

Konstruktion

die 5 Tetrominos

die 35 Hexominos

Bestimmung der Anzahlen

Es gibt verschiedene Ansätze, die Anzahl der Polyominos zu bestimmen. Am Häufigsten wird nur bis auf Kongruenz unterschieden. In praktischen Sachverhalten sind jedoch häufig nur orientierungserhaltende Bewegungen für das Zur-Deckung-Bringen zugelassen, also nur Drehungen und Verschiebungen und keine Achsenspiegelungen. Auch bei dem Spiel Tetris ist dies der Fall. Kongruente Polyominos, die eine unterschiedliche Orientierung besitzen, werden dabei als verschieden angesehen

nicht-orientierungserhaltende Bewegung

nicht-orientierungserhaltende Bewegung

$A(n)$ bezeichnet die Anzahl Polyominos, die sich bis auf Kongruenz aus $n$ Quadraten bilden lassen. $A'(n)$ ist die Anzahl unter Beachtung der Orientierung, d. h. zueinander spiegelbildliche (wie oben illustriert) werden als verschieden betrachtet. $A''(n)$ bezeichnet die Anzahl unter Beachtung der Orientierung und aller möglichen Lagen, dabei werden sogar zwei zueinander gedrehte, aber sonst gleiche Polyominos als verschieden angesehen. Vor allem $A(n)$ ist von Interesse.

$n$	$A(n)$	$A'(n)$	$A''(n)$
1	1	1	1
2	1	1	2
3	2	2	6
4	5	7	19
5	12	18	63
6	35	60	216
7	108	196	760
8	369	704	2725
9	1285	2500	9910
10	4655	9189	36446
11	17073	33896	135268
12	63600	126759	505861
13	238591	476270	1903890
14	901971	1802312	7204874
15	3426576	6849777	27394666

Werden ausschließlich einfach zusammenhängende Polyominos gezählt, so ergeben sich von $n=7$ an abweichende Zahlen.

rekursive Fortsetzung

Algorithmus

Man kann leicht ein rekursives Verfahren beschreiben, das es gestattet, aus der Kenntnis aller $n-1$-Minos $(n \geq 2)$ alle $n$-Minos zu gewinnen. Es lässt sich zunächst zeigen, dass es zu einem $n$-Mino $P_2$ $(n \geq 2)$ ein $n-1$-Mino $P_1$ und ein Quadrat $Q$ gibt, so dass $P_2 = P_1 \cup Q$ ist. Dadurch kann von der Kenntnis der Klassen der $n-1$-Minos ausgegangen werden. Durch Anfügen eines Quadrates entsteht je ein Repräsentant der Klassen der $n$-Minos. Auf diese Weise kann auch die Anzahl $A(n)$ der Klassen bestimmt werden. Wir verfahren wie folgt.

Wir nummerieren die Klassen der $n-1$-Minos durch und beginnen mit einem Repräsentanten $P$ der ersten Klasse, und betrachten systematisch alle Lagen eines Quadrates $Q$, die überhaupt zu einem $n$-Mino $P \cup Q$ führen können. Diese Lagen werden mit oder markiert, je nachdem, ob das entsprechende $n$-Mino zu den bisherigen kongruent ist, oder nicht. Nach gleicher Weise wird bei den nächsten Klassen der $n-1$-Minos verfahren. Natürlich kann dabei ein $n$-Mino entstehen, welches zu einem aus vorangegangenen Schritten kongruent ist. Solche werden mit einem Lagekästchen bezeichnet $(i=1,2,\ldots)$.

Nach endlich vielen Schritten bricht das Verfahren ab und es liefert einen Repräsentanten für jede Klasse der $n$-Minos.

Beispiel

Der rekursive Algorithmus soll bei der Ermittlung der Pentominos aus Tetrominos eingesetzt werden.

Computergestützt

Auf der Grundlage dieses Verfahrens lassen sich die $A(n)$ mit Computern bestimmen. Dabei lassen sich Polyominos durch Matrizen mit 0 und 1 wie in folgendem Beispiel beschreiben.

wird zu $\begin{pmatrix} 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \end{pmatrix}$

Verwendung

Packungen

Welche notwendigen und hinreichenden Bedingungen bestehen für die positiv ganzzahligen Seitenlängen eines Rechteckes, damit dieses mit bestimmten Sorten von Polyominos gepackt werden kann.

Spieleindustrie

Im Deutschen sind das Spiel Domino und im Russischen das Pentomino (Begriff stammt vom amerikanischen Mathematiker Solomon W. Golomb) weit verbreitet. Tetrominos kommen unter anderen in dem vom russischen Programmierer Alexei Paschitnow 1985 entwickelten Computerspiel Tetris zum Einsatz, wobei komplexere Versionen dieses Spiels auch auf andere Polyominos – ggf. Polywürfel – zurückgreifen. Neuere Brettspiele sind das 2000 erschienene Blokus sowie das 2003 in Schweden und 2005 in Deutschland erschienene Ubongo, wo jeweils die verschieden großen $n$-Minos für $n=1..5$ als Spielmaterial verwendet werden. 2001 erschien das Spiel Rumis, welches dreidimensionale Steine verwendet.

Pädagogik

Die Bausteine finden in der Grundschule Verwendung und dienen der Verbesserung der räumlichen Vorstellung. Ziel ist es zu einer vorgegebenen Menge von Bausteinen Figuren zu finden oder für vorgegebene Figuren eine Zerlegung in die entsprechenden Bausteine. Es ist nicht möglich, aus allen 5 möglichen Tetronimos ein 5*4 Rechteck zu erstellen. Es ist auch nicht möglich ohne Mehrfachverwendung eines Winkelstücks ein 4*4 Quadrat aus Tetrominos zu erstellen. Die Figuren werden auch LTZ-Parkette genannt.

Literatur

• Solomon W. Golomb: Polyominoes. Puzzles, Patterns, Problems, and Packings. 2. erweiterte Auflage. Princeton University Press, Princeton 1994, ISBN 0-691-08573-0

Weblinks

• Polyominos bei Wolfram Mathworld
• Gerard's Universal Polyomino Solver
• Puzzlespiel mit Polyominos 3D
• Spiel zur Füllung mit Polyominos 2D
• Ebene Figuren – Vielecke (Anwendung für Kinder)