Lineares zeitinvariantes System
Als ein lineares zeitinvariantes System, auch als LZI-System und LTI-System (englisch linear time-invariant system) wird ein dynamisches Übertragungssystem bezeichnet, wenn sein Ein-/Ausgangsverhalten linear ist und wenn sich die Charakteristik des Systemverhaltens nicht mit der Zeit ändert (Zeitinvarianz).
Die Theorie dieser Systeme hat eine enorme Anzahl von Anwendungen in der realen Welt: Das System kann beispielsweise ein technisches System (aus der Mechanik, Elektrik, Thermodynamik, Nachrichtentechnik, Regelungstechnik und viele mehr), ein biologischer Vorgang oder ein Bestandteil der Volkswirtschaft sein.
Das LZI-System ist ein abstraktes mathematisches Modell von realen Systemen, das interessierende Aspekte der realen Welt für einen bestimmten Zweck ausreichend genau beschreibt. Systeme, die nicht die erforderlichen Eigenschaften wie Linearität und Zeitinvarianz aufweisen, lassen sich häufig auf LZI-Systeme reduzieren: Beispielsweise werden nichtlineare dynamische Systeme häufig in einem gewissen Arbeitspunkt untersucht und dazu im interessierenden Bereich linearisiert.
LZI-Systeme sind in der Regel in der Literatur außerdem kausal und punktkonzentriert. Das führt zu einer weiteren Vereinfachung der Methoden, die für Analyse und Entwurf dynamischer Systeme Verwendung finden.
| Formelzeichen | |
|---|---|
| Vektor der Eingangssignale | |
| Vektor der Zustandssignale | |
| Vektor der Ausgangssignale | |
| Zusammenhang zwischen Eingangs- und Ausgangssignalen, Systemabbildung | |
| Kontinuierliche Zeit | |
| Faktor, Gewicht | |
| Laufindex | |
|
|
Impulsantwort
Gewichtsmatrix |
| Dirac-Impuls | |
|
|
Anfangszeit
Anfangszustand |
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Linearität[Bearbeiten | Quelltext bearbeiten]

Ein System heißt dann linear, wenn ein mit gewichtetes Eingangssignal zu einem entsprechend gewichteten Ausgangssignal führt.
Dann gilt auch, dass sich aus einer Summe von gewichteten Eingangssignalen das Ausgangssignal als entsprechende Summe der ergibt. Das wird als Superpositionsprinzip, oder auch als Überlagerungsprinzip bezeichnet.
Für den mathematischen Zusammenhang zwischen Eingang und Ausgang gilt bei linearen Systemen:
Anschaulich entspricht das folgendem Versuch: Am Eingang des Systems wird ein Signal angelegt und die Reaktion beobachtet. Danach wird davon unabhängig die Reaktion auf ein zweites Signal untersucht. Beim Anlegen eines Eingangssignals, das die Summe aus den beiden zuvor begutachteten Signalen bildet, lässt sich feststellen, dass die Reaktion am Ausgang der Addition der beiden einzelnen Antworten entspricht, wenn das System linear ist.
Wenn ein System linear ist, dann ist auch der Zusammenhang von Ein- und Ausgang mit den internen Zustandsgrößen linear, also der Zusammenhang zwischen und , sowie der Zusammenhang zwischen und .
Zeitinvarianz[Bearbeiten | Quelltext bearbeiten]
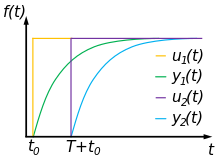
Ein System heißt dann zeitinvariant, wenn für jede beliebige Zeitverschiebung um t0 gilt:
Das bedeutet, dass sich die Charakteristik des Systemverhaltens nicht mit der Zeit ändert. Das Ausgangssignal behält bei einer beliebigen Zeitverschiebung des Eingangssignals den Zeitbezug zum Eingangssignal bei und reagiert darauf identisch. Dieses Prinzip wird auch als Verschiebungsprinzip bezeichnet.
Das Gleiche gilt auch für den Zusammenhang von Ein- und Ausgang mit den internen Zustandsgrößen .
Kausalität und Sprungfähigkeit[Bearbeiten | Quelltext bearbeiten]
Systeme aus dem Anwendungsspektrum der LZI-Systeme sind realisierbar und daher kausal. D.h. im Signalausgang spielen zukünftige Signaleingänge keine Rolle. Der Signaleingang wird als Ursache für den Signalausgang (Wirkung) angesehen. Das entspricht auch dem Kausalprinzip: „Es gibt keine Wirkung ohne Ursache“.

Mathematisch gesehen ist ein System kausal, wenn die Impulsantwort für vergangene Zeiten gleich Null ist:
Den Grenzfall bildet das Thema „Gleichzeitigkeit“: Beispiel: In der Mechanik kommt es bei der Ausübung einer Kraft gleichzeitig zu Kraftreaktionen (Actio und Reactio). Wenn man nur die Signale der gemessenen Kräfte hat, dann ist es eine Sache der Interpretation, welche Kraft die Ursache darstellt und welche die Wirkung.
Verwandt sind die so genannten „sprungfähigen Systeme“, bei denen die Wirkung tatsächlich gleichzeitig mit der Ursache entsteht. Die meisten realen Systeme sind nicht sprungfähig, da sie eine Trägheit aufweisen. Z.B. auch ein elektrisches Signal an einem Sensor kann nicht plötzlich ohne jeden Zeitverzug ansteigen, da ja immer kleine Signalverzögerungen wirken, z. B. durch Kapazitäten in Leitungen oder Bauteilen.
Sprungfähige Systeme können z. B. nur mit Vorsicht mit Differentialgleichungen behandelt werden, da die internen Zustände auf einen plötzlichen Eingang mit unendlicher Steigung reagieren. Aber Sprungfähigkeit bzw. Gleichzeitigkeit ist bei LZI-Systemen durchaus erlaubt.
Kausalität gilt auch für Systeme ohne Eingangsgröße . Die Ursache für den Zeitablauf der Ausgangsgröße ist dann der Startwert der internen Zustandsgrößen . Das ist die so genannte Eigenbewegung des Systems.
Frequenzantwort[Bearbeiten | Quelltext bearbeiten]
Die Antwort eines LZI-Systems auf ein sinusförmiges Eingangssignal ist ebenfalls sinusförmig und hat die gleiche Frequenz. Ein LZI-System kann keine neuen Frequenzen erzeugen (z. B. Oberwellen). Es kann nur die Amplitude des Eingangs-Sinus verändern und eine Zeitverschiebung hinzufügen (Phasengang). Diese Signal-Veränderungen sind oft abhängig von der Frequenz und werden in einem Bode-Diagramm visualisiert.
Nichtlineare Systeme führen dagegen zu einer Signalverzerrung und zu weiteren Frequenzen im Ausgangssignal (Klirrfaktor).
Punktkonzentriert[Bearbeiten | Quelltext bearbeiten]
LZI-Systeme sind Punktkonzentriert, das bedeutet räumliche Ausdehnungen der Energiespeicher in den Systemen spielen keine Rolle. Wenn räumliche Aspekte nicht vernachlässigbar sind, dann benötigt man aufwändigere Mathematik wie z. B. partielle Differentialgleichungen. Als Beispiel sei die Temperaturspeicherung einer Heizwalze gegeben. Bei lokaler Erhitzung breitet sich die Wärme langsam über die Breite der Walze aus: Die Zeitfunktion der Erwärmung hat auch eine ortsabhängige Komponente und hängt auch vom Wärmehaushalt an entfernteren Stellen ab. Bei punktkonzentrierten Systemen werden derartige Aspekte vereinfacht betrachtet.
Punktkonzentrierte Systeme bilden also kein „Kontinuum“, sondern haben eine endliche Anzahl interner Freiheitsgrade bzw. Energiespeicher.
Kommutativität bei Signalflussplan-Umformungen[Bearbeiten | Quelltext bearbeiten]
LZI-Systeme sind im Signalflussplan besonders leicht handhabbar: Beispielsweise können sie vertauscht werden und nach relativ einfachen Regeln innerhalb vom Plan verschoben werden. Durch die Kommutativität lässt sich ein Signalflussplan vereinfachen oder übersichtlicher organisieren. Auch Berechnungen anhand des Signalflussplans fallen leichter.
LZI-Systeme in verschiedenen Darstellungen[Bearbeiten | Quelltext bearbeiten]
Zustandsraumdarstellung im Zeitbereich (kontinuierlich)[Bearbeiten | Quelltext bearbeiten]
| Formelzeichen | |
|---|---|
| Systemmatrix | |
| Eingangsmatrix | |
| Ausgangsmatrix | |
| Durchgangsmatrix | |
| für zeitdiskretes System | |
| Kontinuierliche Zeit | |
| Diskrete Zeit | |
|
|
Kontinuierliche Anfangszeit
Anfangszustand |
| Zeitkonstante eines Systems 1. Ordnung | |
| Abtastzeit des diskreten Systems | |
|
|
Diskrete Anfangszeit
Anfangszustand |
Die gebräuchlichste Systemdarstellung für zeitkontinuierliche stetige Systeme (sog. Differentialsysteme) im Zeitbereich beruht auf inhomogenen linearen Differentialgleichungen mit konstanten Koeffizienten und hat in Zustandsraumdarstellung die Form
Diese Formeln gelten sowohl für Mehrgrößensysteme als auch für Eingrößensysteme. Im Grenzfall ist das System eindimensional (erster Ordnung). Dann sind die Vektoren und Matrizen nur skalare Größen.
Die Matrix wird für sprungfähige Systeme benötigt, d. h., wenn der System-Ausgang ohne Zeitverzug auf einen Systemeingang reagieren kann.
Die allgemeine Lösung dieses Differentialgleichungssystems erhält man direkt über die Lösung des homogenen DGL-Systems und anschließende Variation der Konstanten oder indirekt mit Hilfe der Laplace-Transformation. Sie liefert Zustands- und Ausgangsvektor als Vektorfunktionen zur Zeit in Abhängigkeit vom Vektor der Eingangssignale und vom Vektor des Anfangszustands zur Zeit :
Für den konkreten Fall muss das Integral gelöst und bei mehrdimensionaler Zustandsgröße die als Matrixexponential geschriebene Übergangsmatrix ermittelt werden. Letzteres ist beispielsweise mit Hilfe des Cayley-Hamilton-Theorems, durch Diagonalisierung der Zustandsmatrix oder mithilfe der Laplace-Transformation möglich.[1]
Beispiel: Für ein System 1. Ordnung mit der Zeitkonstante und dem Verstärkungsfaktor sind die Systemparameter gegeben durch , , und . Für eine Sprungantwort zum Zeitpunkt mit der Amplitude und dem Anfangszustand erhält man nach Ausführung der Integration das Ergebnis für den Zeitverlauf des Zustandes für :
Zustandsraumdarstellung im Zeitbereich (diskret)[Bearbeiten | Quelltext bearbeiten]
Die entsprechende Systemdarstellung für zeitdiskrete Mehr- und Eingrößensysteme beruht auf linearen Differenzengleichungen mit konstanten Koeffizienten und hat die Form:[2]
Die Lösung des Differenzengleichungssystems erhält man als Summe der Lösung des homogenen Systems und einer partikulären Lösung, die man mit der Ansatzmethode ermittelt, oder indirekt mit Hilfe der z-Transformation oder einer anderen diskreten Operatorenrechnung. Sie liefert Zustands- und Ausgangsvektor als Vektorfunktionen zum diskreten Zeitpunkt in Abhängigkeit vom Vektor der Eingangssignale und vom Vektor des Anfangszustands zur Zeit :[2]
Für den konkreten Fall müssen die Matrixpotenz der Übergangsmatrix ermittelt und Summe explizit berechnet werden.
Abtastsysteme[Bearbeiten | Quelltext bearbeiten]
Zeitdiskrete Systeme sind in der Regel eigentlich kontinuierlich, aber die Werte von sind nur zu bestimmten Zeitpunkten bekannt. Gleichwertige Schreibweisen sind z. B. für x:
Digitale Mess- oder Steuerungs-Systeme „tasten“ kontinuierliche Mess-Signale in regelmäßigen Zeitabständen ab. Digitalrechner berechnen nicht messbare Größen zu den Abtastzeitpunkten aus den Werten, die bei der vorhergehenden Abtastung gemessen wurden. Man nennt zeitdiskrete Systeme in der Regelungstechnik daher auch Abtastsysteme.[2]
Wenn die Eingangsgröße durch einen Digitalregler erzeugt wurde (Stellsignal), dann wird sie in der Regel in der physikalischen realen Welt zu einem treppenförmigen kontinuierlichen Signal . Der Digitalregler ändert den Wert dieses Signals an den Abtastzeitpunkten - und in den Zwischenpunkten ist das Signal konstant. Dieses Verhalten von Signalausgängen wird auch Sample-and-Hold genannt.
Die Lösung des kontinuierlichen Systems wird mit dem Gedanken des „Sample-and-Hold“ anwendbar auf diskrete Systeme: Jeder Zeitbereich zwischen zwei Abtastungen kann als Sprungantwort aufgefasst werden: Der Anfang dieses Zeitbereichs entspricht der Anfangsbedingung zum Zeitpunkt , das Ende des Zeitbereichs liefert die berechneten Größen zum Zeitpunkt .
Die Lösung der Differenzengleichung für die Abtastzeitpunkte in Abhängigkeit vom Eingangsvektor und den Bedingungen zum Zeitpunkt ist dann:[2]
Diese Lösung, abgeleitet aus der kontinuierlichen Differentialgleichung ist also von der Form:
wobei sich die Parameter des diskreten Systems aus den Parametern des kontinuierlichen Systems berechnen lassen:
Beispiel: Für ein System 1.Ordnung mit der Zeitkonstante und Verstärkungsfaktor sind die Systemparameter des kontinuierlichen Systems gegeben durch und . Die Parameter des diskreten Systems lassen sich dann z. B. durch folgende Formeln berechnen:
Die exakte Berechnung bildet das kontinuierliche Systemverhalten sehr genau ab.Berechnung der Parameter eines diskreten Systems 1. Ordnung Exakte Berechnung (aus Vergleich der Lösungsformeln) Lineare Näherung (nach Linearisierung der e-Funktion) Lineare Näherung (durch Anwendung des Differenzenquotienten) Bilineare Näherung (Tustin-Formel, Trapezregel)
- Die erste lineare Näherung ergibt sich aus einer Reihenentwicklung der e-Funktion (siehe auch Matrixexponential) und ist am einfachsten.
- Die zweite lineare Näherung wird durch Anwendung des Differenzenquotienten auf die DGL hergeleitet.[3]
- Die bilineare Näherung liefert etwas bessere Ergebnisse, als die lineare Näherung, insbesondere, wenn die Abtastzeit in der Größenordnung von ist.[4]
Impulsantwort (kontinuierlich)[Bearbeiten | Quelltext bearbeiten]
Unter einem Dirac-Impuls (Einheitsimpuls) versteht man einen einmaligen „unendlich kurzen“ und „unendlich hohen“ Impuls zum Zeitpunkt , wobei die Fläche unter dem Impuls (das Integral, die „Energie“ des Stoßes) genau ist. Der Dirac-Impuls ist daher keine „normale“ Funktion, sondern eine Distribution.
Die Reaktion eines kontinuierlichen Eingrößensystems auf einen solchen idealen Impuls am Eingang nennt man Impulsantwort, Gewichtsfunktion oder Stoßantwort .
Ein Dirac-Impuls hat die sogenannte „Ausblendeigenschaft“: Bei der Multiplikation von mit einer Dirac-Impuls-Funktion werden alle Werte von außerhalb des Impulses ausgeblendet, also gleich Null. Deshalb ist der Wert der Ergebnisfunktion gleich dem Wert von zum Zeitpunkt des Impulses. Ein beliebig verlaufendes Eingangssignal kann aufgrund dieser Ausblendeigenschaft als Faltungsintegral oder mit dem Symbol für die Faltungsoperation geschrieben werden:
Am Systemausgang kann wegen der Gültigkeit des Superpositionssatzes und der Zeitinvarianz der Systemoperator unter das Integral „geschoben“ werden:
Das Ausgangssignal kann demnach bei Kenntnis der Impulsantwort eines (zeitkontinuierlichen) LZI-Systems als Faltungsintegral mit dem Eingangssignal dargestellt werden:
Deshalb lässt sich ein zeitkontinuierliches Eingrößen-LZI-System durch seine Impulsantwort charakterisieren. Diese repräsentiert damit zusammen mit dem (kommutativen) Faltungsoperator den Systemoperator . Insbesondere ist deren Laplace-Transformierte identisch mit der Übertragungsfunktion des Systems.
Beim Mehrgrößensystem werden die Impulsantworten aller Kombinationen der Eingänge und Ausgänge zur Gewichtsmatrix kombiniert. Aus der allgemeinen Lösung der Zustandsgleichungen kann man diese (unter Beachtung des verschwindenden Anfangszustandes, der Ausblendeigenschaft des Dirac-Impulses und der Sprungfunktion ) sofort ablesen:
Für das oben genannte Beispiel eines PT1-Gliedes erhält man daraus
Neben der Impulsantwort hat ebenfalls die Sprungantwort für die Beschreibung des Systemverhaltens Bedeutung.
Impulsantwort (diskret)[Bearbeiten | Quelltext bearbeiten]
Der diskrete Einheitsimpuls ist ein „einmaliger Impuls“ der Höhe 1 zum Zeitpunkt 0. Die Reaktion eines diskreten Eingrößensystems auf diesen Impuls am Eingang nennt man (diskrete) Impulsantwort, Gewichtsfunktion oder Stoßantwort .
Eine beliebig verlaufende Eingangsfolge kann als Faltungssumme oder mit dem Symbol für die diskrete Faltung geschrieben werden:
Am Systemausgang kann wegen der Gültigkeit des Superpositionssatzes und der Zeitinvarianz der Systemoperator unter das Summenzeichen „geschoben“ werden:
Das Ausgangssignal kann deshalb bei Kenntnis der Impulsantwort eines zeitdiskreten LZI-Systems als Faltungssumme mit dem Eingangssignal dargestellt werden:
Deshalb lässt sich ein zeitdiskretes Eingrößen-LZI-System durch seine Impulsantwort charakterisieren.
Beim Mehrgrößensystem werden die Impulsantworten aller Kombinationen der Eingänge und Ausgänge zur Gewichtsmatrix kombiniert. Aus der allgemeinen Lösung der Zustandsgleichungen kann man diese (unter Beachtung des verschwindenden Anfangszustandes und der Ausblendeigenschaft des Einheitsimpulses) sofort ablesen:
Übertragungsfunktion (kontinuierlich)[Bearbeiten | Quelltext bearbeiten]
| Formelzeichen | |
|---|---|
| Übertragungsfunktion, Übertragungsmatrix | |
| Zählerpolynom | |
| Nennerpolynom | |
| Laplace-Variable, komplexe Frequenz | |
| Variable der z-Transformation | |
| für zeitdiskretes System | |
Erregt man ein einfaches zeitkontinuierliches kausales LZI-Systeme mit nur je einer Ein- und Ausgangsgröße mit der harmonischen Exponentiellen mit der komplexen Frequenz , dann errechnet sich (wie oben gezeigt) das Ausgangssignal durch „Faltung“ mit der Impulsantwort zu
Am Ausgang erhält man also – typisch für ein LZI-System – die in Bezug auf die komplexe Frequenz gleiche harmonische Exponentielle wie am Eingang, nur mit einer zeitunabhängigen Konstante multipliziert. Weil die Impulsantwort aufgrund der Kausalität für verschwindet, ist diese Konstante identisch mit dem Laplace-Integral der Impulsantwort
und man bezeichnet sie als Laplace-Übertragungsfunktion.
Ihre Bezeichnung und ihre Wichtigkeit werden deutlich, wenn man die Gleichung der Laplace-Transformation unterzieht, denn dann erhält man die Ein-/Ausgangsbeziehung des Systems aufgrund der Regeln der Laplace-Transformation als (einfache) Multiplikation im Laplace-„Bildbereich“ oder „Frequenzbereich“:
Die Übertragungsfunktion ist der Ein-/Ausgangs-Operator eines einfachen LZI-Systems im Bildbereich und besitzt die Form einer gebrochen-rationalen Funktion in :
Sie kann als Pol-Nullstellen-Diagramm grafisch dargestellt werden und bietet sich zur Stabilitätsanalyse an. Geht man von der komplexen Frequenz zur imaginären Frequenz über, dann erhält man den Frequenzgang des Systems, der sich zur graphischen Darstellung als Ortskurve oder Bodediagramm eignet.
Bei einem Mehrgrößensystem werden die Übertragungsfunktionen aller Kombinationen der Eingänge und Ausgänge zur Übertragungsmatrix kombiniert. Sie ist die Laplace-Transformierte der Gewichtsmatrix .
Ist ein LZI-System in Zustandsform gegeben, dann kann dessen DGL-System in den Bildbereich transformiert werden und führt bei Annahme eines verschwindenden Anfangszustandes auf rein algebraischem Weg zur Lösung im Bildbereich:
Daraus kann man die Übertragungsmatrix ablesen:
Hieraus erkennt man durch Vergleich mit der Lösung im Zeitbereich eine wichtige Beziehung, die zur Ermittlung des Matrixexponentials genutzt werden kann[1]:
Für das oben genannte Beispiel eines PT1-Gliedes erhält man die bekannte Übertragungsfunktion
Übertragungsfunktionen erlauben auch eine einfache Verschaltung von Systemen und eine grafische Übersicht dieser Verschaltung im Signalflussplan: LZI-Systeme kann man im Signalflussplan in der Reihenfolge vertauschen (kommutativ). Zwei aufeinanderfolgende Systeme kann man im Signalflussplan zusammenfassen, indem man die beiden Übertragungsfunktionen miteinander multipliziert.
Übertragungsfunktion (diskret)[Bearbeiten | Quelltext bearbeiten]
Ausgehend von der Faltung mit der Impulsantwort erfolgt für zeitdiskrete LZI-Eingrößen-Systeme eine entsprechende Definition der Übertragungsfunktion durch eine „diskrete Transformation“ der Zeitsignale in einen Bildbereich.
Haben die Signale des diskreten Systems einen nichtquantifizierten Symbolvorrat (meist den der reellen Zahlen), dann bevorzugt man die z-Transformation
und definiert die z-Übertragungsfunktion als z-Transformierte der (diskreten) Impulsantwort (mit der komplexen z-Ebene als Bildbereich), welche die Form einer gebrochen-rationalen Funktion in besitzt:
Bei einem Mehrgrößensystem werden die Übertragungsfunktionen aller Kombinationen der Eingänge und Ausgänge zur Übertragungsmatrix kombiniert. Sie ist die z-Transformierte der Gewichtsmatrix .
Löst man die Differenzengleichungen der Zustandsraumdarstellung mit Hilfe der z-Transformation und nimmt einen verschwindenden Anfangszustand an, dann entsteht als Lösung im Bildbereich
Daraus lässt sich die Übertragungsmatrix ablesen:
Die Äquivalenz zur Übertragungsmatrix von kontinuierlichen Systemen ist unverkennbar. Außerdem zeigt der Vergleich mit der Lösung im Zeitbereich eine wichtige Beziehung der Fundamentalmatrix und ihre Beziehung zu Laurent-Reihen[1][5]:
Haben die Signale eines diskreten LZI-Systems einen quantifizierten und insbesondere endlichen Symbolvorrat (beispielsweise bei endlichen linearen Automaten), dann ist die auf der Analysis beruhende z-Transformation nicht geeignet und es muss eine rein algebraische Operatorenrechnung verwendet werden. In der Literatur findet man dazu die D-Transformation[6] bzw. die Zeta-Transformation[7].
Beispiele[Bearbeiten | Quelltext bearbeiten]
- Elektrotechnik: Filter-Schaltungen oder Verstärker
- Mechanik: Getriebe
- Thermodynamik: Zentralheizung, Motorkühlung
- Wandler zwischen den zuvor genannten Systemarten: Elektromotor (Strom-Kraft), Temperatursensor (Temperatur-Strom)
- Mathematisch (Digitale Simulation): Regler aller Art z. B. PID-Regler
Beispiel aus der Mechanik[Bearbeiten | Quelltext bearbeiten]
Der freie Fall ohne Reibung wird beschrieben durch die Differentialgleichung
mit dem Weg , der Beschleunigung an der Erdoberfläche und der Masse des fallenden Gegenstandes . Übertragen in die Zustandsraumdarstellung und unter herauskürzen von erhält man die Zustandsdifferentialgleichung
wobei als (in der Regel konstanter) äußerer Einfluss betrachtet wird, und damit ein (das einzige) Glied des Eingangsvektors bildet. Interessiert man sich naheliegenderweise für die momentane Position und Geschwindigkeit , lautet die Ausgangsgleichung
mit einer 1-Matrix als Ausgangsmatrix und einer Nullmatrix als Durchgriffsmatrix, da die Ausgänge identisch mit den Zuständen sind. In dieser Betrachtung handelt es sich um ein LZI-System, da alle Matrizen des linearen Differentialgleichungssystems konstant, also zeitinvariant, sind.
Berücksichtigt man aber, dass die Erdbeschleunigung g abhängig ist vom Abstand der Massenschwerpunkte
mit der Erdmasse und dem Erdradius , so ist das System nichtlinear abhängig vom Zustand z, also kein LZI-System.
Wird die Erdbeschleunigung aufgrund einer meist sehr viel kleineren Höhe gegenüber dem Erdradius weiterhin als konstant betrachtet
aber die Reibung zwischen betrachteter Masse und Luft als sehr viel einflussreicher in linearer Abhängigkeit von linear berücksichtigt (siehe auch Fall mit Luftwiderstand#Fall mit Stokes-Reibung), erhält man die Zustandsdifferentialgleichung
mit dem Reibkoeffizienten . Wird als Formkonstante des fallenden Gegenstandes betrachtet, handelt es sich nach wie vor um ein LZI-System.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Heinz Unbehauen: Regelungstechnik 1, Vieweg, Braunschweig/Wiesbaden, ISBN 3-528-93332-1
- Alan V. Oppenheim, Roland W. Schafer, John R. Buck: Zeitdiskrete Signalverarbeitung, Pearson/München, ISBN 3-8273-7077-9
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b c Rolf Unbehauen: Systemtheorie 1. 8. Auflage. Oldenbourg, München / Wien 2002, ISBN 3-486-25999-7.
- ↑ a b c d J. Ackermann: Abtastregelung. 2. Auflage. Springer-Verlag, Berlin / Heidelberg / New York 1983.
- ↑ Differenzengleichung 1.Ordnung. Abgerufen am 5. September 2023.
- ↑ Control Systems. Abgerufen am 5. September 2023.
- ↑ Gerhard Wunsch, Helmut Schreiber: Analoge Systeme – Grundlagen. Verlag Technik, Berlin 1985, DNB 860626318.
- ↑ Gerhard Wunsch: Handbuch der Systemtheorie. R. Oldenbourg, München Wien 1986, ISBN 3-486-20017-8.
- ↑ Gerhard Wunsch, Helmut Schreiber: Digitale Systeme – Grundlagen. Verlag Technik, Berlin 1982, DNB 840950934.







































































































































