Ziegenproblem (Geometrie)
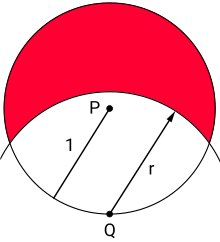
Das Ziegenproblem – auch Die grasende Ziege genannt[1] – ist ein seit dem 18. Jahrhundert bekanntes Problem der Unterhaltungsmathematik. Die erste Veröffentlichung erfolgte 1748 in dem in England einmal jährlich erscheinenden The Ladies Diary: or, the Woman’s Almanack.
Problemstellung
[Bearbeiten | Quelltext bearbeiten]Wie groß muss bei der gezeigten Abbildung sein, damit die rote Fläche die Hälfte der Kreisfläche ist? Konkrete Motivation: Am Punkt sei eine Ziege (oder ein anderes Tier) angebunden. Wie lang muss die Leine sein, damit das Tier auf genau der Hälfte der Kreisfläche grasen kann?
Lösung mit Berechnung der Linsenfläche
[Bearbeiten | Quelltext bearbeiten]Die von der Ziege erreichbare Fläche hat die Form einer asymmetrischen Linse (siehe Berechnungsskizze), die von zwei Kreisbögen begrenzt wird.[2]
Um den Flächeninhalt der durch die zwei Kreisbögen begrenzten Fläche zu bestimmen, kann man diese in zwei Kreissegmente zerlegen, wobei die Trennungslinie in den beiden Schnittpunkten und der Kreisbögen endet. Mit wird der Radius des Kreises, der die Wiese darstellt, und mit derjenige des Kreises, dessen Mittelpunkt auf dem Kreisrand des anderen liegt, und mit wird der Abstand zwischen den zwei Kreismittelpunkten und bezeichnet.
Höhen d1 und d2 der rechtwinkligen Dreiecke MDP bzw. DMQ
[Bearbeiten | Quelltext bearbeiten]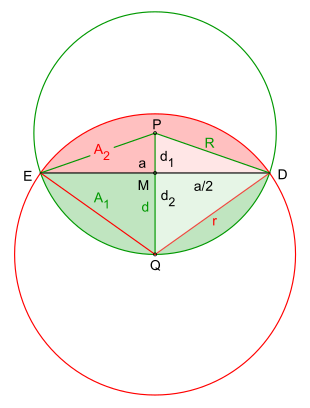
Gegeben: sowie
Nach dem Satz des Pythagoras gilt:
von in eingesetzt ergibt
ausmultipliziert und umgeordnet ergibt
daraus ergibt
wegen wird entsprechend ergänzt
wegen ergibt sich schließlich
Radius r
[Bearbeiten | Quelltext bearbeiten]Mittels zweimaliger Anwendung der Formel für den Flächeninhalt eines Kreissegments mit als Abstand des Kreismittelpunktes bzw. bis zur Kreissehne
und den darin eingesetzten Termen von und von erhält man nach entsprechender Umformulierung die Formel für den Flächeninhalt der asymmetrischen Linse:[3]
Für und halber Kreisfläche vereinfacht sich dies zu
Diese Gleichung kann nur numerisch gelöst werden und ergibt (Folge A133731 in OEIS).
Lösung mit Integration
[Bearbeiten | Quelltext bearbeiten]Aus der Integration über die rechte Hälfte der Linsenfläche mit
ergibt sich die ebenfalls transzendente Gleichung
mit der gleichen Lösung.
Geometrische Näherungslösung
[Bearbeiten | Quelltext bearbeiten]
mit Approximation der halben Wiesenfläche (grün).
die Länge der Leine
Zwei sich schneidende Kreise und deren Schnittpunkt liefern den gesuchten Radius, der die kreisförmige Wiesenfläche nahezu halbiert.
Konstruktion
[Bearbeiten | Quelltext bearbeiten]Es beginnt mit dem Einheitskreis um Punkt und dem Einzeichnen von zwei zueinander senkrecht stehenden Radien; dabei ergeben sich die Schnittpunkte und Es folgt der Kreisbogen um mit Radius Er schneidet den Kreis in und bringt damit den gesuchten Radius als Länge der Strecke Der abschließende Kreisbogen um Punkt mit Radius ab schneidet den Kreis in und liefert nahezu eine Halbierung der Kreisfläche.
Nachrechnung
[Bearbeiten | Quelltext bearbeiten]
Aus der nebenstehenden Berechnungsskizze bzw. aus der obigen Konstruktionsbeschreibung ist zu entnehmen:
- ist der Einheitskreis mit der Gleichung
- ist ein Teil des Kreises mit dem Radius und der Gleichung
- Punkt ist der Schnittpunkt des Kreises mit dem Kreis Die Abstände des Punktes in einem kartesischen Koordinatensystem sind: und
Die Länge der Strecke erhält man durch Subtraktion der beiden Kreisgleichungen:[5]
Die Länge der Strecke erhält man durch Einsetzen des x-Wertes in die Kreisgleichung des Kreises
Somit ist die Länge der Strecke
Für die Hypotenuse des rechtwinkligen Dreiecks gilt nach dem Satz des Pythagoras:
Absoluter Fehler der konstruierten Länge der Leine; darin entspricht Radius dem numerisch gelösten (s. oben):
- [LE]
Für den relativen Fehler des konstruierten Radius gilt:
mit den eingesetzten Werten ergibt sich
Den Radius eingesetzt in die vereinfachte Formel der Linsenfläche für den Einheitskreis (mit ), oben in Lösung mit Berechnung der Linsenfläche beschrieben, ergibt näherungsweise die konstruierte halbe, im Bild grüne, Wiesenfläche
- [FE].
Flächeninhalt der halben Wiese (halber Einheitskreis)
- [FE]
Absoluter Fehler der approximierten halben Wiesenfläche
- [FE]
Relativer Fehler der approximierten halben Wiesenfläche (Formel siehe oben bei )
Verdeutlichung der Approximation
[Bearbeiten | Quelltext bearbeiten]Hätte z. B. die kreisförmige Wiese einen Radius gleich dann wäre die Leine um ca. zu lang und die Ziege könnte – angebunden am Punkt an eine Leine mit der Länge – außer der für sie vorgesehenen Hälfte der Wiesenfläche (rund ), noch zusätzlich abgrasen, das wären etwa weniger als ein DIN-A4-Blatt.
Geschlossene Lösung
[Bearbeiten | Quelltext bearbeiten]Mit Methoden der komplexen Geometrie fand Ingo Ullisch im Jahr 2020 folgende geschlossene Lösung[6][7][8]
Erweiterungen
[Bearbeiten | Quelltext bearbeiten]Die Ziege im Weltall
[Bearbeiten | Quelltext bearbeiten]
Im dreidimensionalen Fall befindet sich Punkt auf der Oberfläche einer Einheitskugel, und die Fragestellung ist, wie groß der Radius der zweiten Kugel sein muss, damit der Schnittkörper genau die Hälfte des Volumens der Einheitskugel hat.
Der vom Tier erreichbare Teil der Einheitskugel hat die Form einer dreidimensionalen Linse mit unterschiedlich gewölbten Seiten, die von den beiden Kugelkalotten begrenzt wird.
Das Volumen einer Linse bei zwei Kugeln mit Radien und Mittelpunktabstand ist:
was sich bei und halbem Kugelvolumen vereinfacht zu
woraus als Lösung folgt
Es kann gezeigt werden, dass sich bei weiter zunehmender Dimensionalität dem Wert annähert.
Die Ziege am Silo
[Bearbeiten | Quelltext bearbeiten]Im zweidimensionalen Fall kann auch die Frage nach der Größe der erreichbaren Fläche außerhalb des roten Kreises gestellt werden. Das entspricht der Situation, dass das Tier an einem Silo festgebunden ist.
In diesem Fall besteht die Fläche aus einem Halbkreis (hellblau) mit Radius und zwei Flächen, die durch den roten Kreis und die Kreisevolvente begrenzt sind (dunkelblau). Aus der Sektorformel von Leibniz folgt der Inhalt einer der dunkelblauen Flächen. Die gesamte erreichbare Fläche (hell- und dunkelblau) beträgt dann
unter der Bedingung, dass (andernfalls überschneiden sich die beiden dunkelblauen Flächen auf der Rückseite des Silos).
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Literatur
[Bearbeiten | Quelltext bearbeiten]- Raymond Clare Archibald: Involutes of a circle and a pasturage problem. In: American Mathematical Monthly, 28, 1921, S. 328–329.
- Marshall Fraser: A tale of two goats. In: Mathematics Magazine, 55, 1982, S. 221–227.
- Jean Jacquelin: Le problème de l’hyperchèvre. In: Quadrature, 49, 2003, ISSN 1142-2785, S. 6–12.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Heinrich Hemme: Die Hölle der Zahlen. 92 mathematische Rätsel mit ausführlichen Lösungen. Vandenhoeck & Ruprecht, Göttingen 2007, ISBN 978-3-525-40841-4, S. 32 und 102 f.
- ↑ a b Eric Weisstein: Goat Problem. WolframMathworld, abgerufen am 17. November 2019.
- ↑ a b c Eric Weisstein: Circle-Circle Intersection. WolframMathworld, abgerufen am 17. November 2019.
- ↑ Eric Weisstein: Circular Segment. WolframMathworld, abgerufen am 17. November 2019.
- ↑ Schnitt und Schnittwinkel zweier Kreise. (PDF) Nichtlineare analytische Geometrie. In: Dimensionen – Mathematik 7. Verlag E. Dorner, Wien, 2016, S. 1, abgerufen am 19. November 2020.
- ↑ Ingo Ullisch: A Closed-Form Solution to the Geometric Goat Problem. In: The Mathematical Intelligencer. 18. Februar 2020, ISSN 0343-6993, doi:10.1007/s00283-020-09966-0 (englisch).
- ↑ Steve Nadis: A After Centuries, a Seemingly Simple Math Problem Gets an Exact Solution. Quanta Magazin, 9. Dezember 2020, abgerufen am 23. Februar 2022.
- ↑ Ingo Ullisch: Correction to: A Closed-Form Solution to the Geometric Goat Problem. Abgerufen am 3. März 2024.






















































![{\displaystyle {\begin{aligned}\;r&={\sqrt {\left(|{\overline {FQ}}|\right)^{2}+\left(|{\overline {FC}}|\right)^{2}}}\\&={\sqrt {\left(1-{\frac {\sqrt {35}}{18}}\right)^{2}+\left({\frac {17}{18}}\right)^{2}}}\Rightarrow \\&={\frac {\sqrt {18-{\sqrt {35}}}}{3}}\Rightarrow \\r&=1{,}158731117161276\ldots [LE]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/740027df190dc22640cd114686b9fedc5d02a808)






























