Diagramm
Ein Diagramm (von altgriechisch διάγραμμα diágramma „geometrische Figur, Umriss“), genannt auch (grafisches) Schaubild,[1][2] ist eine grafische Darstellung von Daten, Sachverhalten oder Informationen. Je nach der Zielsetzung des Diagramms werden höchst unterschiedliche Typen eingesetzt. Die Bandbreite von bildhaften Elementen bis rein abstrakten Gebilden ist dabei sehr groß.
Im Unterschied zum Piktogramm (oder Bildsymbol) wird mit Hilfe eines Diagramms vor allem versucht, einen Zusammenhang zu verdeutlichen, während ein Piktogramm nur für eine gezielte Information steht. Diagramme sind zudem oft codiert, was bedeutet, dass man mit Hilfe seines Vorwissens ein Diagramm analysieren muss, um es verstehen zu können, während ein Piktogramm durch seinen ikonischen (bildlichen) Charakter unmittelbar verständlich ist. Allerdings können Diagramme durchaus Piktogramme enthalten.
Diagramme können in Tabellenkalkulationsprogrammen erstellt werden.
Historische Diagramme[Bearbeiten | Quelltext bearbeiten]
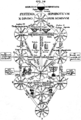
Die Nutzung von Diagrammen ist seit der Antike bekannt. So wurden Graphen zur Darstellung von Verwandtschaftsbeziehungen, religiösen Gedanken oder rechtlichen Beziehungen genutzt. Aber auch Diagramme zur Darstellung von Tonsystemen in musiktheoretischen Handschriften sind schon früh nachgewiesen.[3]
-
Stammbaum Christi als Wurzel Jesse, 1180
-
Guidonische Hand als Tonsystem, 1475
-
Dantes Weg aus dem Fegefeuer, 1515
-
Kabbala, 1652
-
Entwicklungsbaum von Darwin, 1837
Achsendiagramme[Bearbeiten | Quelltext bearbeiten]
Achsendiagramme dienen zur Veranschaulichung von Zusammenhängen zwischen voneinander abhängigen Werten oder Messgrößen in einem Koordinatensystem.
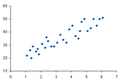
- Punktdiagramm: Zwei normal (senkrecht) aufeinander stehende Koordinatenachsen spannen eine Fläche auf, in die Wertepaare als Punkte (Kreuze, Kreise) eingetragen werden; allgemeiner und in der Statistik auch Streudiagramm.
- Blasendiagramm: Eine Erweiterung des Punktdiagramms: Blasen um jeden Punkt herum (mit verschieden großen Flächen) verbildlichen ein weiteres Merkmal.
- Liniendiagramm: Die Punkte werden miteinander durch Linien (Geraden, Kurven) verbunden; ist die Fläche zwischen Achse und Linie ausgefüllt, spricht man von einem Flächendiagramm.
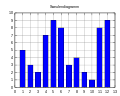
- Säulendiagramm: Der Abstand zwischen der horizontalen Achse und dem Datenpunkt wird mit einer senkrecht auf der Achse stehenden Linie oder rechteckigen Fläche dargestellt.
- Balkendiagramm: Ähnlich dem Säulendiagramm, allerdings mit horizontalen Linien oder Flächen.
-
Punktdiagramm
-
Blasendiagramm
-
Liniendiagramm (bei erkennbarer Gesetzmäßigkeit)
-
Liniendiagramm (bei streuenden Werten)
-
Säulendiagramm
-
Balkendiagramm
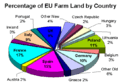
- Kreisdiagramm: Sind die Einzelwerte Teile eines Ganzen, so kann man die Werte in Form von Kreissektoren zeichnen, um darzustellen, welche Anteile die Einzelwerte an dem Ganzen haben.
- Tortendiagramm / Kuchendiagramm: Eine Variante des Kreisdiagramms mit perspektivischer Darstellung eines flachen Kreiszylinders.
- Ringdiagramm: Eine Variante des Kreisdiagramms; mehrere Datenreihen werden in je einem eigenen Ring dargestellt.
- Netzdiagramm: Bei größeren Datenreihen wird für jeden Wert eine Achse gezeichnet, und die Achsen werden gleichmäßig auf 360° um den Nullpunkt verteilt; die Werte werden dann auf den Achsen angetragen und miteinander durch Geraden verbunden, wodurch eine an ein Spinnennetz erinnernde Form entsteht.
- Zeigerdiagramm: Zeigt eine Abhängigkeit nach Betrag und Winkel an und wird meist zur Darstellung von komplexen Zahlen oder von Größen in der Wechselstromtechnik verwendet.
-
Kreisdiagramm
-
Tortendiagramm
-
Ringdiagramm
-
Netzdiagramm
-
Zeigerdiagramm
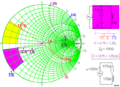
- Smith-Diagramm: Wird zur einfachen grafischen Berechnung von 1/x verwendet. Es entspricht einer Projektion aus dem Liniendiagramm für komplexe, reell positive Werte in eine Kreisform.
- Gantt-Diagramm: Ein Gantt-Diagramm oder Balkenplan ist ein nach dem Unternehmensberater Henry L. Gantt (1861–1919) benanntes Instrument des Projektmanagements, das die zeitliche Abfolge von Aktivitäten grafisch in Form von Balken auf einer Zeitachse darstellt.
- Pareto-Diagramm: Das Pareto-Diagramm zeigt Gruppen nach ihrer Bedeutung geordnet. Siehe auch ABC-Analyse.
-
Smith-Diagramm
-
Gantt-Diagramm
-
Pareto-Diagramm
Darstellung von multivariaten Funktionen f, die von mehreren Variablen abhängen:
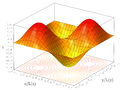
- Orthogonale 3D-Darstellung: Darstellung der Punktetripel (x,y,f(x,y)) durch Parallelprojektion.
- Kurvenschar, Kennlinienfeld: Darstellung durch mehrere Kurven, bei denen eine der Variablen unveränderlich, ein (Parameter) ist.
- Höhenliniendiagramm: Punkte (x,y) mit gleichem Funktionswert f(x,y) werden zu ausgewählten Werten in einem Koordinatensystem wie Höhenlinien in einer Landkarte angegeben.
- Heatmap: Punkten (x,y) in gleichem Funktionswertintervall f(x,y) werden gleiche Farben zugeordnet.
- Dreiecksdiagramm: Jedem Punkt im gleichseitigen Dreieck werden durch Parallelen zu den Seiten drei Werte an den Rändern/Achsen zugeordnet, die zusammen einen konstanten Wert (in der Regel 100 %) ergeben.
-
Orthogonale 3D-Darstellung
-
Kennlinienfeld mit Parameter
-
Höhenlinien in einer Karte
-
Höhenangaben in Regionalfarben (Heatmap)
-
Dreiecksdiagramm der Erstarrungstemperatur einer ternären Metalllegierung
Graphen[Bearbeiten | Quelltext bearbeiten]
In diesem Diagrammtyp geht es um Objekte und deren Beziehungen untereinander. Den mathematischen Unterbau bildet die Graphentheorie.
Zu dieser Kategorie gehören demnach auch Diagramme, die zur Veranschaulichung von Strukturen, beispielsweise Organisationsstrukturen (Organisationsdiagramme, kurz Organigramme), Verwandtschaftsbeziehungen (Stammbaum), Flowcharts, Concept-Maps und Datenstrukturen (Baumdiagramme: Dendrogramm und Entscheidungsbaum) verwendet werden.
Die Sankey-Diagramme zählen zu den gerichteten Graphen. Sie stellen über die Breite der Pfeile zusätzliche Informationen dar.
-
Gerichteter Graph mit Mehrfachkanten
-
Künstlerisch erweiterter Graph
-
Kommutatives Diagramm in der Mathematik
Mengendiagramme[Bearbeiten | Quelltext bearbeiten]
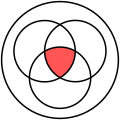
Ein Mengendiagramm auch Venn-Diagramm genannt veranschaulicht vor allem Beziehungen von Mengen zueinander. So können sich diese zum Beispiel beinhalten oder überlappen, was eine Teilmenge oder eine Schnittmenge bedeuten würde. Meistens werden die Mengen als Kreise oder Ellipsen dargestellt.
Figürliche oder kartografische Darstellung[Bearbeiten | Quelltext bearbeiten]
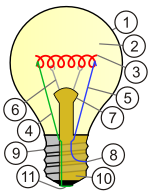

Eine figürliche Darstellung ist meist eine schematische Zeichnung eines realen Objekts mit dem Zweck, einen bestimmten Sachverhalt zu erklären. Es werden aber auch Fotos als Grundlage verwendet, welche allerdings mit zeichnerischen Mitteln und Piktogrammen (wie Pfeilen, Nummerierungen …) versehen werden.
Diese Art der Darstellung wird im gleichen Maße Illustration oder technische Zeichnung genannt. Die Fläche, in der diese Darstellung erfolgt, wird entsprechend auch Zeichenebene genannt. Die Abgrenzung der Bezeichnungen ist in der deutschen Sprache nicht klar. Es lassen sich aber Tendenzen ablesen. Diagramm wird eher für schematische, Illustration eher für künstlerische und technische Zeichnung eher für maßstäbliche Darstellungen verwendet.
Kartografische Diagramme werden z. B. bei der Darstellung von Erdschichten oder Höhenlagen eingesetzt, aber auch als Stadtplan oder Ähnliches.
In den USA muss für jeden Flughafen, der einen Tower hat, ein airport diagram erstellt und über die FAA publiziert werden. Diese Diagramme werden alle 28 Tage aktualisiert. Als Beispiel ist hier das Diagramm des John F. Kennedy International Airport in New York zu sehen (zur Legende siehe Abkürzungen/Luftfahrt).
Spezielle Diagrammtypen[Bearbeiten | Quelltext bearbeiten]
Technik[Bearbeiten | Quelltext bearbeiten]

Abläufe in Produktionsanlagen werden mittels Prozessdiagramm oder Ablaufplan dargestellt. Dieser enthält alle Maschinen und Leitungen in einer schematischen, ikonisierten Darstellung. Spezielle (genormte und nicht genormte) Symbole machen es möglich, den Plan einer Fabrik oder Produktionsanlage zu „lesen“. Beispiele hierfür sind das Reinigungsdiagramm und das Vermahlungsdiagramm einer Mühle.
Weitere typische Diagrammtypen in der Technik sind der Schaltplan in der Elektronik sowie das Verfahrensfließschema und das Rohrleitungs- und Instrumentierungsfließschema im verfahrenstechnischen Anlagenbau. Letztere beiden Fließbilder sind in EN ISO 10628 genormt.
Physik[Bearbeiten | Quelltext bearbeiten]
Im Bereich der Physik gibt es einige spezielle Diagramme:
- Feynman-Diagramm
- Grotrian-Diagramm (Termschema)
- Hertzsprung-Russell-Diagramm (Stellarphysik)
- Minkowski-Diagramm
- Mollier-h-x-Diagramm
Finanzwesen[Bearbeiten | Quelltext bearbeiten]
Besondere Diagramme finden sich auch bei der Chartanalyse an der Börse, wobei die Diagramme hier als Charts bezeichnet werden. Ein Zeit-Kosten-Fortschritts-Diagramm zeigt den aktuellen Stand der Kosten, der geplanten Termine sowie den Projektfortschritt, um so auf eventuelle Abweichungen aufmerksam zu machen.
Informatik[Bearbeiten | Quelltext bearbeiten]

Diagramme können aber auch dazu dienen, Abläufe übersichtlich und logisch darzustellen (Ablaufdiagramme). Dies ist insbesondere in der Informatik wichtig (siehe Unified Modeling Language). Die bekanntesten Darstellungsformen sind hier das Flussdiagramm und das Struktogramm.
Statistik[Bearbeiten | Quelltext bearbeiten]
Im Bereich der Statistik sind folgende Diagramme recht verbreitet:
- Histogramm
- Säulendiagramm (bzw. Stabdiagramm)
- Box-Plot: Kombinierte Auftragung von Mittelwert und Quantilen
- Korrelogramm
- Mosaik-Plot: Darstellung eines Datensatzes mit mehreren kategoriellen Variablen
- Summenhäufigkeitspolygon: Näherung der empirischen Verteilungsfunktion
Diagrammerstellung per Software[Bearbeiten | Quelltext bearbeiten]
Diagramme können heutzutage mit Office-Programmen oder mit Visualisierungsprogrammen erstellt werden. Dabei können auch Formatierungen und ähnliche Veränderungen abhängig von der Leistungsfähigkeit der Programme erzeugt werden. Viele Statistik-Programme bieten ebenso Funktionen zum Erzeugen von Diagrammen aus den vorliegenden Daten.
Manipulation[Bearbeiten | Quelltext bearbeiten]

Durch die Art der grafischen Darstellung kann ein Diagramm versuchen, die Analyse des Betrachters in eine bestimmte Richtung zu lenken, ohne dass dieser es merkt. Ein Diagramm kann auf Fakten beruhen, aber dennoch beim Betrachter einen manipulierten Eindruck entstehen lassen. Dies kann zum Beispiel durch die Wahl der Achsen geschehen: kleine Unterschiede können überbetont werden, indem der Nullpunkt eines Achsendiagramms verschoben wird.
Ein anderes Beispiel ist der Börsenverlauf. Wenn die Aktienkurse an einem Tag rapide und schnell fallen, kann ohne nähere Angabe des Notierungszeitraums der Eindruck eines Börsencrashs entstehen. Verfolgt man den Börsenverlauf über das ganze Jahr hin, bemerkt man, dass das tägliche Auf und Ab der Börsenkurse normal ist. Beim Vergleich zwischen Kursentwicklung und Benchmark sind Manipulationen sehr beliebt, da hier oft ein indexierter Chart eingesetzt wird.
Diagrammatik[Bearbeiten | Quelltext bearbeiten]
Die Diagrammatik ist ein Forschungsfeld, das sich damit beschäftigt, wie Daten und Erkenntnis mit Hilfe von Diagrammen dargestellt, vermittelt und erläutert werden können.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
- Abszisse
- Achsenbeschriftung
- Affinitätsdiagramm
- Bland-Altman-Diagramm
- Eisen-Kohlenstoff-Diagramm
- Funktion (Mathematik)
- Nassi-Shneiderman-Diagramm (Flussdiagramm)
- Ikonische Wende
- Kennlinie
- Koordinatensystem
- Logarithmische Darstellung
- Ordinate
- Prozessvisualisierung (Darstellung von Prozessen und Abläufen)
- Semiotik
- Skalenniveau
- Visualisierung
- Visualisierungsprogramme
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Liste aller Wikipedia-Artikel, deren Titel mit Diagramm beginnt
- Liste aller Wikipedia-Artikel, deren Titel Diagramm enthält
- Bildstatistiken Diagramme. Teachsam.de, abgerufen am 27. November 2015 (Erklärungen und mehr zu verschiedenen Diagrammformen).
- Visualisierungstechniken. Universität Tübingen, abgerufen am 27. November 2015.
- Verfügbare Diagrammtypen. microsoft.com, 2010, archiviert vom (nicht mehr online verfügbar) am 3. Mai 2010; abgerufen am 27. November 2015 (englisch, Erklärungen zu verfügbaren Diagrammtypen unter Office 2007).
- Info Design Patterns. fh-potsdam.de, 30. Juli 2008, archiviert vom (nicht mehr online verfügbar) am 17. Januar 2009; abgerufen am 27. November 2015 (englisch, Interaktive Seite mit Filterfunktion die verschiedene Visualisierungsformen aufzeigt. Mit Beschreibungen, Anwendungsbeispielen und Beispieldarstellungen).
- Wolfgang Walla: Wie man sich durch statistische Grafiken täuschen lässt. (PDF) Statistisches Landesamt Baden-Württemberg, 2008, abgerufen am 14. April 2020 (Erklärungen zu Manipulationen von Diagrammen).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Schaubild. duden.de
- ↑ Claudia Nöllke: Präsentieren. 5., aktualisierte Auflage. Haufe, Freiburg 2010, ISBN 978-3-448-10026-6, S. 61–65: Grafische Schaubilder (Diagramme).
- ↑ Ute von Figura: Diagramme in musiktheoretischen Handschriften – Charakteristika und Entwicklung. Universität Heidelberg. Materiale Textkulturen. materiale-textkulturen.de, 3. Juni 2019; abgerufen am 10. Januar 2020