Rotationsellipsoid
 |
 |
Ein Rotationsellipsoid (englisch spheroid) ist eine Rotationsfläche, die durch die Drehung einer Ellipse um eine ihrer Achsen entsteht. Anders als bei einem dreiachsigen bzw. triaxialen Ellipsoid sind zwei Achsen gleich lang.
Je nachdem, welche der beiden Halbachsen der erzeugenden Ellipse als Drehachse fungiert, werden unterschieden:
- das abgeplattete (oblate) Ellipsoid bei Rotation um die kleine Halbachse (Beispiel: Form einer Schokolinse)
- das verlängerte (prolate) Ellipsoid bei Rotation um die große Halbachse (Beispiel: Form des Rugbyballs).
Vorkommen
[Bearbeiten | Quelltext bearbeiten]
Die meisten größeren Himmelskörper sind angenähert abgeplattete Rotationsellipsoide, die auch Sphäroide genannt werden. Sie entstehen durch die Fliehkraft, die bewirkt, dass ein sich drehender kugelförmiger Körper verformt wird. An den Polen, also den Durchstoßpunkten der Rotationsachse, werden diese Körper abgeplattet, am Äquator entsteht eine Ausbauchung. Besonders deutlich ist die Abplattung bei den großen Gasplaneten Jupiter und Saturn ausgeprägt, weil sie besonders schnell rotieren und nicht verfestigt sind. Aber auch die Erde und die anderen Planeten des Sonnensystems werden durch die bei der Rotation entstehenden Fliehkräfte zu Rotationsellipsoiden verformt. Der in zehn Stunden rotierende Jupiter ist um etwa 1/16 abgeplattet, die Erdabplattung beträgt 1/298,257223563 (WGS 84).
Elliptische Galaxien sind oft keine Rotationsellipsoide, sondern triaxial.
Parameterdarstellung
[Bearbeiten | Quelltext bearbeiten]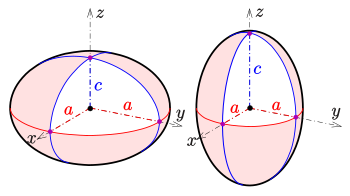
Die folgende Parameterdarstellung beschreibt ein Rotationsellipsoid, das durch Rotation der Halb-Ellipse (in der --Ebene) um die -Achse entsteht (s. Rotationsfläche):
- .
Die Zahlen sind die Halbachsen der rotierenden Halbellipse. Im Fall entsteht ein abgeplattetes Rotationsellipsoid, im Fall ein verlängertes Rotationsellipsoid. Falls ist, ergibt sich eine Kugel mit Radius .
Man beachte: Die Pole (Punkte auf der Rotationsachse) besitzen keine eindeutige Darstellung.
Das entstandene Rotationsellipsoid besitzt die implizite Darstellung:
Volumen
[Bearbeiten | Quelltext bearbeiten]Das Volumen des obigen Rotationsellipsoids beträgt
- .
Dabei ist der Radius des Äquatorkreises und der Abstand der Pole vom Mittelpunkt.
Oberfläche
[Bearbeiten | Quelltext bearbeiten]Die Oberfläche[1] für das abgeplattete Ellipsoid () berechnet man mit
die des verlängerten Ellipsoids () mit
Eine Kugel mit Radius hat das Volumen und die Oberfläche (s. Kugel).
- Herleitung der Formeln
Der Inhalt des Flächenmantels einer durch Rotation der Kurve erzeugten Rotationsfläche ist
- (siehe Rotationsfläche)
Für das obige Rotationsellipsoid ist . Es muss also das Integral
(2-mal ein halbes Ellipsoid) berechnet werden. Für ist und es ergibt sich die Oberfläche einer Kugel. Im Folgenden wird vorausgesetzt.
Die Substitution mit führt zu
und damit zu
- falls , und
- falls .
Unter Beachtung, dass der Bruch unter der Quadratwurzel in beiden Fällen positiv ist, ergeben sich mit Hilfe einer Integrationstabelle (z. B. Bronstein-Semendjajew) die Stammfunktionen für die beiden Integrale und schließlich die oben angegebenen Formeln für die Oberfläche.
Anwendung
[Bearbeiten | Quelltext bearbeiten]In der Geodäsie, Kartografie und den anderen Geowissenschaften werden Rotationsellipsoide als geometrische Annäherung an das physikalische Geoid benutzt. Diese Rotationsellipsoide dienen dann als Referenzfläche, um die Lage bzw. Höhe von Objekten der Erdoberfläche anzugeben. Man spricht dann von einem Referenzellipsoid.
In einem Hohlkörper reflektieren die Begrenzungsflächen des (gestreckten) Rotationsellipsoids die Strahlung von einem Brennpunkt zum anderen. Den Effekt nutzt ein Flüstergewölbe für die Bündelung von Schallwellen.
Derart geformte optische Reflektoren bündeln die Strahlung einer nahezu punktförmigen, sich in einem der Brennpunkte befindlichen Lichtquelle auf den anderen Brennpunkt des Ellipsoids. Dort kann sich die Grenzfläche eines Lichtleitkabels, ein anderes optisches Element oder der Ort eines strahlungsinduzierten Prozesses befinden.
Anwendungsbeispiele
[Bearbeiten | Quelltext bearbeiten]Jupiter und Saturn
[Bearbeiten | Quelltext bearbeiten]Die Planeten Jupiter und Saturn sind wegen den durch die schnelle Rotation wirkenden Zentrifugalkräfte an den Polen deutlich flacher als am Äquator und haben annähernd die Form eines Rotationsellipsoids.
Jupiter
[Bearbeiten | Quelltext bearbeiten]Jupiter hat den Äquatordurchmesser 142984 km und den Poldurchmesser 133708 km. Also gilt für die Halbachsen und . Die Masse des Jupiter beträgt etwa 1,899 · 1027 kg. Daraus ergibt sich mithilfe der oben genannten Formeln für das Volumen, die mittlere Dichte und die Oberfläche:
- Volumen:
- Das ist etwa 1321-mal so viel wie das Volumen der Erde.
- Mittlere Dichte:
- Jupiter hat also insgesamt eine etwas höhere Dichte als Wasser unter Standardbedingungen.
- Oberfläche:
- Das ist etwa 121-mal so viel wie die Oberfläche der Erde.
Saturn
[Bearbeiten | Quelltext bearbeiten]Saturn hat den Äquatordurchmesser 120536 km und den Poldurchmesser 108728 km. Also gilt für die Halbachsen und . Die Masse des Saturn beträgt etwa 5,683 · 1026 kg. Daraus ergibt sich:
- Volumen:
- Das ist etwa 764-mal so viel wie das Volumen der Erde.
- Mittlere Dichte:
- Saturn hat also insgesamt eine etwas geringere Dichte als Wasser unter Standardbedingungen.
- Oberfläche:
- Das ist etwa 84-mal so viel wie die Oberfläche der Erde.
Rugbyball
[Bearbeiten | Quelltext bearbeiten]Ein Rugbyball hat eine Länge von etwa 280 Millimetern und an der Nebenachse einen Durchmesser von etwa 200 Millimetern. Also gilt für die Halbachsen und . Die Masse eines Rugbyballs beträgt etwa 400 Gramm. Daraus ergibt sich:
- Volumen:
- Mittlere Dichte:
Kuppel des Berliner Reichstagsgebäudes
[Bearbeiten | Quelltext bearbeiten]
Die nach der Deutschen Wiedervereinigung neu errichtete Kuppel des Berliner Reichstagsgebäudes hat die Form eines halben Rotationsellipsoiden mit einem Durchmesser von 38 Metern an der Nebenachse und einer Höhe von 23,5 Metern. Also gilt für die Halbachsen und . Daraus ergibt sich das Volumen
Siehe auch
[Bearbeiten | Quelltext bearbeiten]Weblinks
[Bearbeiten | Quelltext bearbeiten]Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Beyer, CRC Handbook of Mathematical Sciences, 5th Edition, S. 198.
- ↑ Georg Glaeser: Geometrie und ihre Anwendungen in Kunst, Natur und Technik, 4. Auflage, Springer Spektrum, Springer-Verlag GmbH Berlin 2022, ISBN 978-3-662-64382-2, Seite 233
- ↑ Guide zum Reichstag Berlin Tourist Information, abgerufen am 3. Oktober 2022













































