Zeitinvarianz
Zeitinvarianz oder Zeitunabhängigkeit bezeichnet die Eigenschaft eines mathematischen Objekts, sich im Zeitablauf nicht zu ändern, obwohl die Modellierung der möglichen Zeitabhängigkeit Bestandteil dieses mathematischen Objektes ist. Typische Verwendungsbereiche des Konzeptes der Zeitinvarianz sind die Theorie stochastischer Prozesse und die Systemtheorie. Ein mathematisches Objekt, das die Eigenschaft der Zeitinvarianz hat, wird als zeitinvariant bezeichnet.
Zeitinvarianz in der Theorie stochastischer Prozesse[Bearbeiten | Quelltext bearbeiten]
Ein stochastischer Prozess , bei dem ein Zeitindex und eine Menge von Zeitpunkten ist, besitzt eine Wahrscheinlichkeitsverteilung (oder kurz Verteilung), die durch die endlichdimensionalen Verteilungen festliegt. Im Allgemeinen ändern sich die endlichdimensionalen Verteilungen im Zeitablauf.
Sind alle endlichdimensionalen Verteilungen zeitinvariant, so liegt ein stochastischer Prozess vor, der im stationär im engeren Sinn ist. Die Zeitinvarianz für die eindimensionalen Verteilungen bedeutet, dass die Zufallsvariablen für alle Zeitpunkte dieselbe Verteilung besitzen, die eindimensionalen Verteilungen sind also zeitinvariant. Die Zeitinvarianz für die zweidimensionalen Verteilungen bedeutet, dass die Verteilung unabhängig von der Lage in der Zeitachse ist, also nur von der Differenz der beiden Zeitpunkten abhängt. Für je zwei verschiedene Zeitpunkte und jede zeitliche Verschiibung mit der Eigenschaft haben die Paare von Zufallsvariablen und dieselbe Verteilung. Analog wird die Zeitinvarianz für alle höherdimensionalen Verteilungen definiert; siehe dazu stationärer stochastischer Prozess.
Ein stochastischer Prozess ist stationär im weiteren Sinn, wenn die Erwartungswertfunktion endlich und konstant ist, und die Kovarianz von zwei Zufallsvariablen und nur von der Zeitdifferenz abhängt. Die Erwartungswertfunktion ordnet jedem Zeitpunkt den Erwartungswert der Zufallsvariablen zu, formal ist dies die Funktion
- .
Die Erwartungswerte der Zufallsvariable eines stochastischen Prozesses variieren im Allgemeinen im Zeitablauf. Falls
- für alle
gilt, sind die Erwartungswerte der Zufallsvariablen zeitinvariant. Dies ist genau dann der Fall, wenn die Erwartungswertfunktion konstant ist. Die Kovarianzfunktion ordnet je zwei Zeitpunkten die Kovarianz der Zufallsvariablen und zu, d. h.
- .
Die Kovarianz zweier Zufallsvariablen eines stochastischen Prozesse variieren mit den beiden Zeitindizes. Falls
für alle Zeitverschiebungen mit der Eigenschaft gilt, ist die Kovarianz zweier Zufallsvariablen eine zeitinvariante Eigenschaft, da sie bei Zeitverschiebungen unverändert bleibt.
Zeitinvarianz in der Systemtheorie[Bearbeiten | Quelltext bearbeiten]
Die Zeitinvarianz ist in der Systemtheorie die Eigenschaft eines Systems, zu jeder Zeit das gleiche Verhalten bei gleicher Eingabe zu zeigen – es ist über die Zeit invariant. Die Parameter seiner mathematischen Beschreibung sind zeitlich unveränderlich, und die Matrizen der Zustandsraumdarstellung sind konstant.
Ein System ist ein Gebilde mehrerer Elemente, die eine Einheit bilden, z. B. eine elektronische Schaltung oder ein Pendel. Die Parameter eines Systems sind dann die Kenngrößen der elektronischen Bauteile oder geometrische Abmessungen.
Gemeinsam mit der Linearität vereinfacht sich die Systembeschreibung damit zu den linearen, zeitinvarianten Systemen.
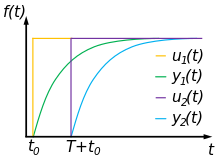
Aus der Systemeigenschaft Zeitinvarianz folgt, dass die zeitliche Verschiebung des Eingangssignals des Systems zu einer gleichartigen Verschiebung des Ausgangssignals führt, ohne dessen zeitlichen Verlauf in anderer Form zu beeinflussen.
Das heißt, das System
liefert auf ein Eingangssignal , das um die Zeit verzögert wurde, ein gleiches, entsprechend verzögertes Ausgangssignal :
Ein System, das die oben beschriebene Eigenschaft nicht besitzt, wird als zeitvariant bezeichnet.
Energieerhaltung[Bearbeiten | Quelltext bearbeiten]
Nach dem Noether-Theorem gehört in der Physik zu jeder kontinuierlichen Symmetrie auch eine Erhaltungsgröße. Zur Zeitinvarianz (Homogenität der Zeit) gehört die Energieerhaltung.
Beispiele für zeitlich invariante Systeme sind abgeschlossene Systeme, z. B. ein ideales Pendel ohne Berücksichtigung der Reibung. Bei diesem ändern sich zwar zusammen mit der Geschwindigkeit des Pendels (also des Systems) seine kinetische Energie und mit dessen Lage im Raum seine potentielle Energie zeitlich, jedoch bleibt deren Summe, die Gesamtenergie, konstant. Es ist egal, zu welchem Zeitpunkt das Pendel betrachtet wird; seine Energie E ist immer gleich:
Beispiele[Bearbeiten | Quelltext bearbeiten]
1. Beispiel Ein elektrischer Widerstand R ist zeitinvariant. Fließt durch ihn ein konstanter Strom I, dann fällt an ihm eine Spannung U von ab. Auch mehrere Minuten später liegt an ihm die gleiche Spannung an.
Bei genauerer Betrachtung ist die Spannung geringfügig höher, weil sich der Widerstand durch den Stromfluss erwärmt hat. Diese Erwärmung ist aber nicht direkt von der Zeit abhängig, sondern von dem Eingangssignal Strom, der Wärmeabgabe und der Ausgangstemperatur. Unter gleichen Ausgangsbedingungen wird er zu jeder Zeit die gleiche Spannung liefern.
2. Beispiel Man stelle sich folgende zwei Systeme vor:
- System A:
- System B:
Da System A eindeutig von t abhängt, ist dieses zeitvariant. Das System B ist nicht direkt von t abhängig und ist deswegen zeitinvariant.













![{\displaystyle \mu (t)=\mathrm {E} [X_{t}],\quad t\in \mathbb {T} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e94caf1f6cb0ded0764106cec2f2b4d0870c1a2b)



![{\displaystyle \gamma (t,t')=\mathrm {Cov} [X_{t},X_{t'}],\quad t,t'\in \mathbb {T} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f4956167ad04664e560bbc499e7126a1ea8c2c5)













