Pentaeder
Als Pentaeder (von griech.: Fünfflächner oder Fünfflach) werden in der Geometrie beschränkte, konvexe Polyeder bezeichnet, die durch fünf Flächen begrenzt sind. Weil ein Pentaeder grundsätzlich nur entweder aus einem Viereck und vier Dreiecken, oder aus drei vierecken und zwei Dreiecken bestehen kann, gibt es zwei Gruppen. Die erste Gruppe bilden die Viereck-Pyramiden. Die andere Gruppe hat verschiedene Unterteilungen. Sind die beiden Dreiecke gleich groß und parallel und die Vierecke Parallelogramme, so zählen diese Körper zu den Prismen. Sind die Dreiecke und die sie verbindenden Vierecke wie bei einem Prisma verteilt, aber die bei einem Prisma parallelen Kanten nicht (oder nicht alle) parallel, so spricht man von einem verzerrten oder gestauchten Prisma (englisch truncated prism).[1][2]
Die gezeigten Beispiele erfüllen (wie jeder beschränkte, konvexe Polyeder) die Eulersche Polyederformel. Beschränkt ist jeder Polyeder, bei dem auch die größte Entfernung zwischen zwei Eckpunkten endlich ist, also sich mit einem Zahlwert beziffern lässt. „Konvex“ bedeutet, dass es keine einander zugewandten Außenseiten gibt.
Sämtliche Pentaeder entsprechen der mathematischen Definition eines Keils, als eines Körpers, bei dem an mindestens einer Kante zwei Flächen im spitzen Winkel, also unter 90°, aneinanderstoßen.
| Gruppe | Name | Bild | Ecken | Kanten | Art der Flächen |
|---|---|---|---|---|---|
| regelmäßige Pentaeder | Quadratische Pyramide mit gleichseitigen Seitendreiecken = regelmäßiges Hemioktaeder |
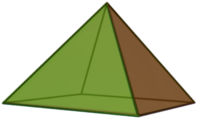
|
5 | 8 | 4 gleichseitige Dreiecke 1 Quadrat |
| regelmäßiges Dreiecksprisma | 
|
6 | 9 | 2 gleichseitige Dreiecke 3 Quadrate | |
| weitere Pyramide mit 4 Symmetrieebenen | gerade quadratische Pyramide | 
|
5 | 8 | 4 kongruente gleichschenklige Dreiecke 1 Quadrat |
| Pyramiden mit 2 Symmetrieebenen | gerade Pyramide mit rhomboider Grundfläche, gerade rhombusbasierte Pyramide |

|
5 | 8 | 4 paarweise kongruente Dreiecke 1 Rhombus |
| gerade Rechteckpyramide | 
|
5 | 8 | 4 paarweise kongruente gleichschenklige Dreiecke 1 Rechteck | |
| Pyramiden ohne Symmetrieebenen | schiefe Rechteckpyramide | 
|
5 | 8 | 4 unterschiedliche Dreiecke 1 Rechteck |
| vierseitige Pyramide mit unregelmäßiger Basis | 
|
5 | 8 | 4 unterschiedliche Dreiecke 1 unregelmäßiges Viereck | |
| weitere Dreiecksprismen | gerades Dreiecksprisma | 
|
6 | 9 | 2 kongruente Dreiecke 3 Rechtecke |
| schiefes Dreiecksprisma | 
|
6 | 9 | 2 kongruente Dreiecke 3 Parallelogramme | |
| sonstige Körper mit zwei parallelen Flächen | Pyramidenstumpf mit dreieckiger Grundfläche | 
|
6 | 9 | 2 ähnliche Dreiecke 3 Trapeze |
| mehr oder weniger unregelmäßige Körper mit der Flächenkomposition eines Dreiecksprismas | verzerrte (gestauchte) Dreiecksprismen (in älterer Literatur auch „abgestumpftes Dreiecksprisma“)[3][4] | 
|
6 | 9 | 2 verschiedene Dreiecke 2 Trapeze 1 Rechteck |

|
6 | 9 | 2 verschiedene Dreiecke 3 Trapeze | ||

|
6 | 9 | 2 verschiedene Dreiecke 3 unregelmäßige Vierecke |
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Pentahedron. In: MathWorld (englisch).
- Pentahedron Zauberwürfel in der Pentaeder-Version.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ google.de Google Buchsuche gestauchtes Prisma → stark verzerrtes (gestauchtes) Prisma in ZNB (1985): Ralf Hoffmann et al. Neue Oxide des Formeltyps A2[T304]: Rb2Li2Si04[1] und Rb2Li2Ge04[2]
- ↑ Google-Buchsuche gestauchtes Prisma → „gestauchtes tetragonales (rhombisches) Prisma“. In: Zeitschrift für Kristallographie. Band 162, 1983, S. 263–27. Akademische Verlagsgesellschaft. A. Kutoglu: Kristallstruktur der Calcium-Vanadium-Bronze CaxV~jVt~2x05
- ↑ Kontext-bezogene Übersetzungen von „truncated“, 2. Eintrag: truncated prism
- ↑ Google Buchsuche „abgestumpftes Prisma“. Carl Dupin: Geometrie und Mechanik der Künste und Handwerke. 1825, S. 136 (Berechnung von Körperinhalten) „… das abgestumpfte Prisma ABCDEF …“.