Satz von Ramsey

Der Satz von Ramsey (nach Frank Plumpton Ramsey) beantwortet die Frage, ob in einem Graphen zwingend gewisse Unterstrukturen auftreten. Genauer werden gefärbte vollständige Graphen auf das Auftreten monochromatischer Teilgraphen hin betrachtet, und es stellt sich heraus, dass solche für hinreichend große Graphen tatsächlich auftreten müssen. Eine praktische Anwendung ist das Spiel Sim.

Erheblich schwieriger als die reine Existenzaussage gestaltet sich die genaue Quantifizierung, was hierbei als „hinreichend groß“ zu betrachten ist, d.h. die genaue Berechnung oder wenigstens Abschätzung der Ramsey-Zahlen.

Aussage des Satzes

Wir betrachten einen vollständigen Graphen mit $n$ Ecken, dessen Kanten mit zwei Farben, etwa rot und blau, gefärbt wurden. Gibt es hierin $r$ Ecken, so dass alle Kanten zwischen diesen rot sind, so sagen wir, der Graph enthalte einen roten $r$-Teilgraphen, entsprechend für blaue Teilgraphen. Mit diesen Bezeichnungen behauptet der Satz von Ramsey:

Seien $r,b$ natürliche Zahlen. Jeder hinreichend große vollständige Graph, dessen Kanten rot oder blau gefärbt wurden, enthält einen roten $r$-Teilgraphen oder einen blauen $b$-Teilgraphen. „Hinreichend groß“ bedeutet hierbei $n\geq N$ für eine von $r$ und $b$ abhängige Zahl $N$. Die kleinstmögliche Zahl, die für $N$ gewählt werden kann, heißt Ramsey-Zahl und wird mit $R(r,b)$ bezeichnet. Umgekehrt ist es also möglich, den vollständigen Graphen mit $R(r,b)-1$ Ecken so zu färben, dass man weder einen roten $r$-Teilgraphen noch einen blauen $b$-Teilgraphen erzeugt.

Der Satz gilt auch in verallgemeinerter Form für mehr als zwei Farben. Entsprechend gibt es auch zu Färbungen mit $c$ Farben gehörige Ramsey-Zahlen $R(n_1,\ldots, n_c)$.

Beispiele

• Allgemein gilt $R(r,b)=R(b,r)$, wie man durch Vertauschen der Farben erkennt.
• $R(k, 1) = 1$: Jeder Teilgraph mit nur einer Ecke ist automatisch monochrom.
• $R(k, 2) = k$: Entweder sind alle Kanten rot oder es gibt eine blaue Kante.

Berechnung von $R(3,3)$

Eine 2-Färbung des K₅ ohne monochromatisches K₃

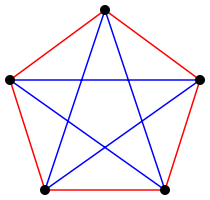
Das nebenstehende Bild zeigt, dass es möglich ist, den $K_5$, also den vollständigen Graphen mit fünf Ecken, so mit zwei Farben rot und blau zu färben, dass weder ein rotes noch ein blaues Dreieck auftritt. Folglich gilt gewiss: $R(3,3)>5$ bzw. $R(3,3)\geq 6$.

Betrachtet man umgekehrt einen auf beliebige Weise rot-blau gefärbten $K_6$ und hierin eine beliebige Ecke $v$, so tritt bei den fünf in $v$ endenden Kanten eine der beiden Farben, oBdA. rot, mindestens dreimal auf (Schubfachprinzip). Ist eine der Kanten zwischen den drei entsprechenden Endpunkten rot, so haben wir ein rotes $K_3$. Andernfalls sind alle Kanten zwischen diesen drei Endpunkten blau, und wir haben ein blaues $K_3$. In jedem rot-blau-gefärbten $K_6$ findet man also ein rotes $K_3$ oder ein blaues $K_3$, d.h., es gilt: $R(3,3)\leq 6$.

Insgesamt erhält man also $R(3,3)=6$.

Die hier gemachten Überlegungen zeigen bereits wesentliche Gedanken für einen Beweis des Satzes sowie eine einfache rekursive Abschätzung für Ramsey-Zahlen, die jedoch für eine exakte Bestimmung der Ramsey-Zahlen nicht ausreicht:

$R(r,b)\leq R(r-1,b)+R(r,b-1).$

Veranschaulichung

Die Ramsey-Zahl $R(r,b)$ beantwortet die Frage, wie viele Personen man z. B. zu einer Party einladen muss, damit sich $r$ Gäste untereinander nicht kennen oder $b$ Gäste sich kennen. „Kennen“ ist in diesem Beispiel eine symmetrische Relation, d. h., wenn Person A Person B kennt, so kennt B auch A.

Betrachten wir beispielsweise $R(3,2) = 3$. Mit $r = 3$ und $b = 2$ folgt $R(3,2) = 3 = N$ (siehe oben).

Haben wir also $N = 3$ Gäste, so können wir nun den vollständigen Graphen $K_{3}$ zeichnen und das Färben beginnen. Man muss jede Kante entweder rot oder blau färben (rot: Gäste kennen sich nicht, blau: Gäste kennen sich) und erreicht folgende mögliche Färbungen:

• Alle Kanten werden rot gefärbt.
• Alle Kanten werden blau gefärbt.
• Zwei Kanten werden blau gefärbt und eine rot.
• Zwei Kanten werden rot gefärbt und eine blau.

Für die drei Gäste bedeutet dies:

• Keiner kennt einen anderen.
• Alle drei kennen sich.
• Eine Person kennt zwei Personen, die einander nicht kennen.
• Zwei Personen kennen sich, aber nicht die dritte Person.

Diese Beschreibung dient lediglich zur Veranschaulichung. Die Analogie zu den Gästen behandelt nicht Probleme, die seltsame „Kennen-sich(-nicht)“-Beziehungen haben (alle kennen sich nicht, zwei kennen sich, aber wer ist der 3.) Ebenso wird nicht berücksichtigt, dass evtl. Person A Person B kennt, aber Person B Person A nicht kennt. Außerdem werden keine transitiven Beziehungen dargestellt.

Literatur

• F. P. Ramsey: On a problem of formal logic. In: Proc. London Math. Soc. series 2, Bd. 30 (1930), S. 264–286

Weblinks

• Ramsey@Home ist ein "BOINC"-Projekt, das durch Verteiltes Rechnen versucht, neue untere Grenzen für Ramsey-Zahlen zu finden.
• Ramsey-Theorie
• Radziszowski’s survey of small Ramsey numbers (eng; PDF-Datei; 109 kB)
• Survey of directed-graph Ramsey numbers (eng)