Eulersche Gleichungen (Kreiseltheorie)

Die Euler’schen Kreiselgleichungen oder uneindeutig Euler’schen Gleichungen sind Bewegungsgleichungen für die Rotation eines starren Körpers. Es sind die Komponenten des für den Starrkörper in seinem Hauptachsensystem aufgeschriebenen Drallsatzes und stellen die wichtigste Grundgleichung der Kreiseltheorie dar.

Wird der Körper einem Drehmoment ausgesetzt, entwickeln sich Kreiselwirkungen, die versuchen die Eigendrehung mit der erzwungenen Drehung in Deckung zu bringen. Die Kreiselwirkungen sind die summierten Drehmomente der Eulerkräfte und Zentrifugalkräfte an allen Massenpunkten des Körpers. Das Moment und die Kreiselwirkungen befinden sich im dynamischen Gleichgewicht, was die Kreiselgleichungen ausdrücken:

${\begin{aligned}M_{1}=&\Theta _{1}{\dot {\omega }}_{1}+(\Theta _{3}-\Theta _{2})\omega _{2}\omega _{3}={\dot {L}}_{1}+\left({\frac {1}{\Theta _{2}}}-{\frac {1}{\Theta _{3}}}\right)L_{2}L_{3}\\M_{2}=&\Theta _{2}{\dot {\omega }}_{2}+(\Theta _{1}-\Theta _{3})\omega _{3}\omega _{1}={\dot {L}}_{2}+\left({\frac {1}{\Theta _{3}}}-{\frac {1}{\Theta _{1}}}\right)L_{3}L_{1}\\M_{3}=&\Theta _{3}{\dot {\omega }}_{3}+(\Theta _{2}-\Theta _{1})\omega _{1}\omega _{2}={\dot {L}}_{3}+\left({\frac {1}{\Theta _{1}}}-{\frac {1}{\Theta _{2}}}\right)L_{1}L_{2}\end{aligned}}$

Darin sind jeweils für $k=1,2,3$

$M_{k}$ die von außen angreifenden Drehmomente,

$\Theta _{k}$ die Hauptträgheitsmomente,

$L_{k}=\Theta _{k}\omega _{k}$ die Drehimpulse,

$\omega _{k}$ die Winkelgeschwindigkeiten und

${\dot {\omega }}_{k}$ die Winkelbeschleunigungen

im Hauptachsensystem. Gelegentlich wird auch die dazu gehörige Vektorgleichung

${\vec {M}}=\mathbf {\Theta } \cdot {\dot {\vec {\omega }}}+{\vec {\omega }}\times \mathbf {\Theta } \cdot {\vec {\omega }}={\frac {\mathrm {d} _{r}}{\mathrm {d} t}}{\vec {L}}+{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\times {\vec {L}}$

mit dem Trägheitstensor $\mathbf {\Theta }$ als Euler’sche Kreiselgleichung angegeben. Hier bildet „·“ die Vektortransformation, „ד das Kreuzprodukt und ${\tfrac {\mathrm {d} _{r}}{\mathrm {d} t}}$ die relative Zeitableitung im Hauptachsensystem.

Die Drehmomente, Hauptträgheitsmomente und Drehimpulse werden mit einem Bezugspunkt berechnet, für den sich der Massenmittelpunkt oder ein unbeschleunigter, in einem Inertialsystem ruhender Stützpunkt eignen, siehe Drallsatz am starren Körper.

Die ersten Summanden auf den rechten Seiten, bestehend aus den Winkelbeschleunigungen und Drehimpulsänderungen, resultieren aus den Kreiselwirkungen der Euler-Kräfte und die anderen, in den Winkelgeschwindigkeiten und Drehimpulsen quadratischen Terme berücksichtigen die Kreiselwirkungen der Zentrifugalkräfte. Wenn die Bewegung bekannt ist, dann können aus diesen Gleichungen die Momente berechnet werden, die im Bezugspunkt eingeleitet werden müssen, damit der Körper die vorgegebene Bewegung ausführt.

Die Kreiselgleichungen wurden von Leonhard Euler 1750 aufgestellt und später zum Drallsatz weiterentwickelt.

Spezialfälle

Euler-Poisson-Gleichungen

→ Hauptartikel: Euler-Poisson-Gleichungen

Die Euler-Poisson-Gleichungen sind die spezifischen Kreiselgleichungen für den schweren Kreisel, bei dem das äußere Moment von der Schwerkraft herrührt. Die klassische Kreiseltheorie ist fast ausschließlich dem schweren Kreisel mit Stützpunkt gewidmet und es wurde viel Aufwand in das Auffinden exakter Lösungen gesteckt. Eine Auflistung einiger dieser Lösungen findet sich im Hauptartikel.

Kugelkreisel

Ein Kugelkreisel ist ein Kreisel mit drei identischen Hauptträgheitsmomenten Θ, sodass sich die Kreiselgleichungen dann auf

${\vec {M}}=\Theta {\dot {\vec {\omega }}}$

reduzieren. Die Winkelbeschleunigung ist beim Kugelkreisel also parallel zum angreifenden Moment. Beim Kugelkreisel sind die Fliehkräfte im Körper immer im mechanischen Gleichgewicht. Ein Vergleich mit den Bewegungsgleichungen bei einer Translationsbewegung zeigt, dass der Kugelkreisel das genaue Analogon des Massenpunkts bei Rotationsbewegungen ist.

Ebene Bewegungen

Bei einer ebenen Bewegung um eine Hauptträgheitsachse, beispielsweise die 3-Achse, entfallen Drehungen und Momente um die 1- und 2-Achsen, und die Gleichungen reduzieren sich auf

$M_{3}=\Theta _{3}{\ddot {\varphi }}\,,$

wobei φ der Drehwinkel um die 3-Achse ist.

Lösungen der Kreiselgleichungen bei ebenen Bewegungen

Im ebenen Fall sind die Kreiselgleichungen oftmals analytisch lösbar, wofür die beiden folgenden Fälle Beispiele sind.

Anstoß einer Billardkugel

Abb. 1: Anstoß einer Billardkugel parallel zur Tischplatte

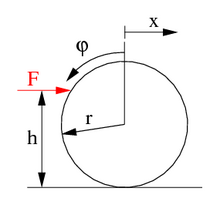
Parallel zur Tischplatte soll eine Billardkugel mit Radius r, Masse m und Massenträgheitsmoment Θ so angestoßen werden, dass sie nicht über den Tisch rutscht, siehe Abb. 1. Es stellt sich die Frage, in welcher Höhe h über der Platte die Kraft F eingeleitet werden muss, damit für das schlupflose Rollen keine Reibkraft am Tisch notwendig ist.

Die exzentrisch an der Kugel angreifende horizontale Kraft entwickelt ein Moment M = -(h-r)F um den Massenmittelpunkt, das die Kugel gemäß der Kreiselgleichung

$M=-(h-r)F=\Theta {\ddot {\varphi }}$

in Drehung versetzt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels φ wirkt. Außerdem beschleunigt die Kraft die Kugel gemäß dem Gesetz „Kraft gleich Masse mal Beschleunigung“:

$F=m{\ddot {x}}\,.$

Die Beschleunigung ${\ddot {x}}$ ist parallel zum Tisch in Richtung der Kraft. Die Bedingung für schlupfloses Rollen

${\ddot {x}}=-r{\ddot {\varphi }}$

schließt das Gleichungssystem für die drei Unbekannten h, φ und x ab. Damit berechnet sich

$-(h-r)F=\Theta {\ddot {\varphi }}=-{\frac {\Theta }{r}}{\ddot {x}}=-{\frac {\Theta }{mr}}F\quad \rightarrow \quad h=r+{\frac {\Theta }{mr}}\,.$

Bei einer massiven homogenen Kugel ist das Massenträgheitsmoment Θ = ²⁄₅mr² und somit

$h={\frac {7}{5}}r={\frac {7}{10}}d\,,$

wobei d = 2r der Durchmesser der Kugel ist.

Ein eine schiefe Ebene hinabrollendes Rad

Abb. 2: Ein eine schiefe Ebene hinab rollendes Rad.

In einer ebenen Bewegung rolle ein Rad mit Radius r, Masse m und Massenträgheitsmoment Θ eine mit dem Winkel α geneigte Ebene unter Einfluss einer Schwerebeschleunigung g hinab, siehe Abb. 2. Weil sich das Rad dabei auch translatorisch bewegt, geht auch seine Masse in die Beschleunigung ein. Die Beschleunigung wächst jedoch, wenn das Massenträgheitsmoment abnimmt.

Aufgrund des schlupflosen Abrollens entsteht am Aufstandspunkt des Rades eine Reibkraft R, die das Rad in Drehung versetzt, denn es entspricht einem Moment M=-r R um den Massenmittelpunkt. Das Moment ist negativ, weil es entgegen der Zählrichtung des Drehwinkels φ arbeitet. Damit lautet die Kreiselgleichung im ebenen Fall:

$-rR=\Theta {\ddot {\varphi }}\,.$

Die auf das Rad hangabwärts wirkende Komponente F der Gewichtskraft mg hat die Größe F=mgsin(α). Ihr entgegen steht die Reibkraft, sodass nach dem zweiten newtonschen Gesetz gilt:

$F-R=m{\ddot {x}}\quad \rightarrow \quad R=mg\sin(\alpha )-m{\ddot {x}}\,,$

worin ${\ddot {x}}$ die hangabwärts zählende Beschleunigung des Rades und sin die Sinusfunktion ist. Die Bedingung für schlupfloses Rollen ${\ddot {x}}=-r{\ddot {\varphi }}$ schließt das Gleichungssystem für die drei Unbekannten R, φ und x ab und es ergibt sich

${\ddot {x}}={\frac {mr^{2}}{\Theta +mr^{2}}}g\sin(\alpha )$

Ein hangabwärts, reibungsfrei rutschender Klotz erfährt die Beschleunigung ${\ddot {x}}=g\sin(\alpha )$, die größer ist als die des Rades, denn beim Rad wird ein Teil der potentiellen Energie in Rotationsenergie umgesetzt, die dann für die Translation fehlt.

Beispiel: Fliehkraftpendel

Ein bemerkenswerter Spezialfall der Euler’schen Kreiselgleichungen ist die "Perle auf rotierendem Kreisring im Schwerefeld", das konische oder Fliehkraftpendel, denn es hat überraschende Eigenschaften. In Worten der Kreiseltheorie handelt es sich um einen schweren Kreisel, der in einem Punkt festgehalten wird und bei dem die Eigendrehung um die Pendelachse durch äußere Momente verhindert und die Präzessionsgeschwindigkeit konstant gehalten wird. Die besonderen Eigenschaften treten bei beliebiger Lage des Massenmittelpunkts und anfänglicher Ausrichtung der Hauptachsen auf. Vereinfachungen ergeben sich mit Massenmittelpunkt auf der 1-Achse und permanent horizontaler 3-Achse des Hauptachsen­systems.

Kinematik

Vom Euler-Kreisel werden die Basiseinheitsvektoren und die Bezeichnungen der Winkel übernommen. Die 1-Achse trägt den Massenmittelpunkt (s := s₁ > 0, s_2,3 = 0). Die Winkelgeschwindigkeiten lauten bei horizontaler 3-Achse (ϑ ≡ 90°):

${\begin{aligned}\mu :=&{\dot {\psi }}=p\sin(\varphi )+q\cos(\varphi ),\;{\dot {\vartheta }}=p\cos(\varphi )-q\sin(\varphi )\equiv 0\\p=&\mu \sin(\varphi ),\;q=\mu \cos(\varphi ),\;r={\dot {\varphi }}\end{aligned}}$

Der Winkel ϑ ist unveränderlich, wenn er anfangs keine Zeitableitung hat und dauerhaft keine Beschleunigung erfährt.

Kinetik

Die Hauptträgheitsmomente seien A, B und C um die 1-, 2- bzw. 3-Achse. Im Hauptachsensystem wirken zusätzlich zum Schweremoment äußere Momente M_1,2 in 1- bzw. 2-Richtung, um Winkelbeschleunigungen von ϑ und ψ zu unterdrücken. Die Kreiselgleichungen in 1- und 2-Richtung dienen nur der Bestimmung dieser Momente, die hier jedoch nicht interessieren. Bemerkenswert ist jedoch, dass diese Drehmomente eine zeitliche Änderung des vertikalen Drehimpulses bedingen, der bei schweren Kreiseln immer konstant ist. Um die 3-Richtung kann das Pendel frei drehen und die dritte der Kreiselgleichungen

${\dot {r}}={\frac {1}{C}}[-mgs\cos(\varphi )-(B-A)pq]$

formuliert mit den Euler-Winkeln liefert dafür die Bewegungsgleichung:

${\ddot {\varphi }}={\frac {1}{C}}[(A-B){\mu }^{2}\sin(\varphi )-mgs]\cos(\varphi )$		(*)

Gleichgewichtslagen

Im Gleichgewicht verschwindet in (*) die Winkelbeschleunigung:

$C{\ddot {\varphi }}=[(A-B){\mu }^{2}\sin(\varphi )-mgs]\cos(\varphi )=0$.

Anders als beim sich selbst überlassenen Lagrange-Kreisel ist eine Präzession mit waagerechter Achse (φ = 0) unmöglich. Mangels Eigendrehung gibt es hier keine Kreiselwirkung, die das Schweremoment ausgleichen könnte. Das Gleichgewicht mit lotrechter 1-Achse (φ = ±90°) ist allen Kreiseln zugänglich – auch dem Kugelkreisel, der nur dort Gleichgewicht findet. Bei A ≠ B ergeben sich die Gleichgewichtslagen aus

$\left[\sin(\varphi )-{\frac {mgs}{(A-B){\mu }^{2}}}\right]\cos(\varphi )=0$

Wenn A - B dasselbe Vorzeichen wie sin(φ) hat, kann der Term in der eckigen Klammer null werden. Dazu muss

$|\sin(\varphi )|\leq 1\quad \leftrightarrow \quad {\mu }^{2}\geq {\frac {mgs}{|A-B|}}=:\mu _{c}^{2}$

erfüllt sein. Der Kreisel muss eine kritische Drehgeschwindigkeit μ_c überschreiten, damit diese Gleichgewichtslage abseits der Senkrechten existiert. Beim abgeplatteten Kreisel weist die 1-Achse im Gleichgewicht nach oben (ist A > B und sin(φ) > 0) und beim gestreckten nach unten (ist A < B und sin(φ) < 0).

Das Hauptträgheitsmoment A gehört zur 1- oder Pendelachse, die den Massenmittelpunkt enthält, und B zur 2-Achse, die zur Pendelachse und zur horizontalen 3-Achse senkrecht ist. Analog zum symmetrischen Kreisel wird das Pendel hier und im folgenden abgeplattet genannt, wenn A > B, und gestreckt, wenn B > A.

Energiebetrachtung

Multiplikation der Bewegungsgleichung (*) mit ${\dot {\varphi }}$ ermöglicht eine Zeitintegration:

$E={\frac {C}{2}}{\dot {\varphi }}^{2}+{\frac {B-A}{2}}{\mu }^{2}\sin ^{2}(\varphi )+mgs\sin(\varphi )$

Die Integrationskonstante E ist die Energie des Pendels im rotierenden System:

• der erste Summand trägt die Rotationsenergie um die 3-Achse bei,
• der zweite Summand ist das Zentrifugalpotential der Präzession und
• der dritte Summand steht für die Lageenergie im Schwerefeld der Erde.

Die Energie und ihre Ableitungen (·)' nach φ ergeben sich mit der Abkürzung $z:={\tfrac {mgs}{(A-B){\mu }^{2}}}$ zu

${\begin{aligned}E=&{\frac {C}{2}}{\dot {\varphi }}^{2}+(B-A)\mu ^{2}{\bigg (}{\frac {\sin ^{2}(\varphi )}{2}}-z\sin(\varphi ){\bigg )}\\E':=&(B-A)\mu ^{2}[\sin(\varphi )-z]\cos(\varphi )\\E'':=&(B-A)\mu ^{2}[1+z\sin(\varphi )-2\sin ^{2}(\varphi )]\end{aligned}}$

Beim gestreckten Kreisel ist B > A und z < 0 und beim abgeplattenten Kreisel ist B < A sowie z > 0. Stabilität liegt in einem Energieminimum vor, wo E' = 0 und E" > 0 ist. Die Energie ist stationär in #Gleichgewichtslagen bei φ = 90°, φ = -90° oder wo sin(φ) = z:^▼

Aufrechtes Pendel φ = 90°

Hier ist E" = (A-B)μ²(1-z). Der obere Totpunkt ist beim gestreckten Kreisel stabil, wenn z > 1, also nie, und beim abgeplatteten, wenn z < 1 oder |μ| > |μ_c|.

Hängendes Pendel φ = -90°

Hier ist E" = (A-B)μ²(1+z). Der untere Totpunkt ist beim gestreckten Kreisel stabil, wenn z < -1, also |μ| < |μ_c|, und beim abgeplatteten, wenn z > -1, also immer. Die Pitchfork-Bifurkation tritt nur beim gestreckten Kreisel auf. Im Gegensatz dazu ist der lotrecht hängende Lagrange-Kreisel immer stabil, siehe dort.

Gleichgewichtslage mit sin(φ) = z

Hier ist E" = (A-B)μ²(z²-1). Diese Position ist beim gestreckten Kreisel stabil, wenn z² < 1, also immer, und beim abgeplatteten, wenn z² > 1, also nie.

^▼ Es genügt nur den Bereich -90° ≤ φ ≤ 90° zu betrachten, da die Bewegung vom Präzessionswinkel ψ unabhängig ist.

Schwingungen

Die Gleichung (*) kann um #Gleichgewichtslagen φ₀, wo z = sin(φ₀) ist, linearisiert werden. Dazu wird φ = φ₀+δ mit konstantem φ₀ und kleiner Abweichung δ angenommen. Die Drehbeschleunigung

$C{\ddot {\varphi }}=C{\ddot {\delta }}=(A-B){\mu }^{2}\sin(\varphi _{0}+\delta )\cos(\varphi _{0}+\delta )-mgs\cos(\varphi _{0}+\delta )$

entwickelt sich mit den Additionstheoremen und sin(δ) ≈ δ, cos(δ) ≈ 1 zur Schwingungsgleichung

${\ddot {\delta }}+{\frac {B-A}{C}}{\mu }^{2}\cos ^{2}(\varphi _{0})\delta =0$

Beim gestreckten Kreisel ist B > A und der Rückstellterm immer positiv, weswegen der gestreckte Kreisel kleine Schwingungen um Gleichgewichtslagen ausführen kann. Beim abgeplattenten Kreisel ist wegen B < A der Rückstellterm negativ. Daher kann der abgeplattete Kreisel keine Schwingungen um Gleichgewichtslagen abseits der Senkrechten ausführen, was im Einklang mit den Ergebnissen aus der #Energiebetrachtung ist.

Siehe auch

• Poinsotsche Konstruktion: grafische Beschreibung der momentenfreien Bewegung.
• Physikalisches Pendel

Literatur

• Herbert Goldstein, Charles P. Poole, Jr, John L. Safko: Klassische Mechanik. 3. Auflage. Wiley-VCH, Weinheim 2006, ISBN 3-527-40589-5. 
• K. Magnus: Kreisel. Theorie und Anwendungen. Springer, Berlin / Heidelberg / New York 1971, ISBN 3-540-05198-8, S. 49. 
• R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 45 (archive.org – „Schwung“ bedeutet Drehimpuls, „Drehstoß“ Drehmoment und „Drehwucht“ Rotationsenergie). 
  oder
  R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. 2. überarb. Auflage. 1: Die Theorie des Kreisels. Springer, Berlin / Göttingen / Heidelberg 1950, DNB 451641299, S. 23. 
• V. I. Arnol’d (В. И. Арнолъд): Mathematische Methoden der klassischen Mechanik. Birkhäuser Verlag, Basel 1988, ISBN 978-3-0348-6670-5, S. 95 f., doi:10.1007/978-3-0348-6669-9 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 14. Februar 2018] russisch: Математическе методы классическоя механики. Moskau 1979. Übersetzt von Prof. Dr. Peter Möbius, TU Dresden). 
  oder
  V. I. Arnol’d: Mathematical Methods of Classical Mechanics. 2. Auflage. Springer, New-York / Berlin / Heidelberg / London / Paris / Tokyo 1989, ISBN 3-540-96890-3, S. 150. 
• Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 3-642-88414-8, S. 4, doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 7. Juni 2019]). 

Weblinks

Commons: Kreisel – Sammlung von Bildern, Videos und Audiodateien

• Interaktive Animationen von Kreisel- und Pendelbewegungen (englisch).