Ising-Modell


Das Ising-Modell ist ein von Ernst Ising auf Anregung seines Doktorvaters Wilhelm Lenz 1924[1] erstmals genauer untersuchtes Gittermodell in der theoretischen Physik. Es beschreibt insbesondere den Ferromagnetismus in Festkörpern (Kristallen). Das Ising-Modell zählt zu den meistuntersuchten Modellen der statistischen Physik. Ising-Modelle können mit Monte-Carlo-Simulationen untersucht werden oder durch die Beschreibung als zellulärer Automat.
Definition[Bearbeiten | Quelltext bearbeiten]
In dem Modell wird angenommen, dass die Spins, welche das magnetische Moment der Atome oder Ionen bestimmen, nur zwei diskrete Zustände annehmen können (Spinwert ). Die Richtung im Raum bleibt aber offen; es handelt sich also um Vektoren (um im klassischen Bild zu bleiben, bzw. quantenmechanisch um Vektoroperatoren).
Der allgemeine Energieausdruck (oder Hamiltonoperator) für eine solche Situation ist durch das Heisenberg-Modell gegeben:
- . [2]
Hierbei bezeichnet
- einen (mehrkomponentigen) Spin des Atoms am Platz des Kristallgitters,
- die Kopplungskonstante (Stärke der Austauschkopplungs-Wechselwirkung) zwischen den Spins an den Plätzen und ,
- der Punkt das Skalarprodukt
- die Stärke des Magnetfeldes.
Beim Ising-Modell dagegen wird die Zahl der Spinkomponenten auf Eins reduziert (d. h. parallel oder antiparallel zu einer ausgezeichneten Achse – hier -Achse): :
- .
Oft wird zusätzlich angenommen, dass nur für benachbarte Spins ungleich Null ist. Ist die Austauschkopplung positiv, so spricht man von einer ferromagnetischen Kopplung; ist sie negativ, so wird sie antiferromagnetisch genannt. Bei Ferromagneten bzw. Antiferromagneten dominiert das jeweilige Vorzeichen; bei den Spingläsern kommen beide Vorzeichen gleich häufig vor.
Durch geeignete Wahl der Wechselwirkungen können u. a. Spingläser (hierbei ist eine Zufallsgröße), verdünnte Magnete mit interessanten kritischen Eigenschaften oder auch räumlich modulierte magnetische Strukturen (hierbei liegen konkurrierende Kopplungen vor, siehe ANNNI-Modell[3]) modelliert werden. Im Allgemeinen beschreibt das Ising-Modell die magnetischen Ordnungen bei tiefen Temperaturen, die bei höheren Temperaturen jedoch durch thermische Fluktuationen aufgebrochen werden, wobei ein Phasenübergang stattfindet. Eine umfassende theoretische Analyse von Phasenübergängen liefert die Theorie der Renormierungsgruppen, für die Kenneth G. Wilson 1982 den Nobelpreis für Physik erhielt.
Bei der eindimensionalen Ising-Kette mit hinreichend kurzreichweitigen Wechselwirkungen beobachtet man jedoch keinen Phasenübergang. Dies hatte schon Ernst Ising in seiner Doktorarbeit mit Bedauern feststellen müssen. Fälschlicherweise vermutete er, dass dies auch für zwei und mehr Dimensionen zutrifft, was zunächst allgemein akzeptiert wurde.
Rudolf Peierls zeigte jedoch 1936,[4] dass in zwei Dimensionen sehr wohl ein Phasenübergang vorlag. 1941 bestimmten Hendrik Anthony Kramers und Gregory Wannier[5] durch ein Dualitätsargument die kritische Temperatur. Die exakte Lösung des zweidimensionalen Ising-Modells mit Wechselwirkungen zwischen nächsten Nachbarn und bei verschwindendem Magnetfeld wurde erstmals 1944 von Lars Onsager berechnet.[6] Weitere Verbesserungen stammten von Bruria Kaufman (teilweise mit Onsager zusammen) und Chen Ning Yang, der 1952 die spontane Magnetisierung exakt berechnete.[7] Eine kombinatorische Behandlung stammt von Mark Kac und John Clive Ward (1952),[8] und der Beweis der Äquivalenz zu einem Fermionenmodell von Elliott Lieb, Theodore David Schultz und Daniel Charles Mattis (1964).[9]
Für das dreidimensionale Ising-Modell mit Wechselwirkungen zwischen benachbarten Spins gibt es keine analytisch-exakte Lösung. Seine Eigenschaften kann man jedoch mit Hilfe der Molekularfeldnäherung (oder Landau-Theorie), Monte-Carlo-Simulationen, Reihenentwicklungen oder anderen numerischen Lösungsverfahren berechnen.
Das Ising-Modell gilt wegen seiner konzeptionellen Einfachheit und seiner vielfältigen Eigenschaften als „Drosophila“ der statistischen Physik. Es hat darüber hinaus Anwendungen in vielen Bereichen der Naturwissenschaften gefunden, bis hin zur Biologie und Hirnforschung. Die nahezu programmatische Aussage von Michael E. Fisher ‚Ising models still thrive‘ (etwa: ‚Ising-Modelle sind noch im Wachsen‘) wird wohl noch für viele Jahre gültig bleiben.
Verallgemeinerungen des Ising-Modells liefern das Blume-Capel-Modell, das Potts-Modell und das Markow-Netzwerk.
Vereinfachte Darstellung[Bearbeiten | Quelltext bearbeiten]
Die wesentlichen Eigenschaften des Ising-Modells lassen sich erläutern anhand des zweidimensionalen Ising-Modells mit Wechselwirkung nur zwischen direkten Nachbarn (links, rechts, oben, unten) in Abwesenheit eines externen Magnetfelds ().
In diesem speziellen Fall kann die Energie eines Zustands beschrieben werden durch:
mit
- der konstanten Anzahl der möglichen Nachbarpaare
- der Anzahl Nachbarpaare mit unterschiedlicher Ausrichtung, die von der Ausrichtung der einzelnen Spins abhängt ().
Die konstante Energie des Grundzustands trägt nicht zum thermodynamischen Verhalten des Systems bei. Entgegengesetzte Nachbarspins liefern einen Energiebeitrag , parallele Spins liefern keinen Beitrag.
Energie, Wärme, Wahrscheinlichkeit[Bearbeiten | Quelltext bearbeiten]

Das Bild zeigt symbolisch einen winzigen „Magneten“ aus 25 „Eisen-Atomen“. Eisenatome verhalten sich wie kleine Magnete. Das Magnetfeld des Gesamtmagneten ist die Summe der Magnetfelder, die von den einzelnen Atomen ausgehen, wobei die Felder entgegengesetzt ausgerichteter Atome einander aufheben.
Fünf der Atome (schwarz) sind hier in eine Richtung ausgerichtet, die restlichen 20 (weiß) in die andere Richtung. Die Nettomagnetisierung ist somit Einheiten. Ein bestimmtes Schwarz-Weiß-Muster bezeichnet man als den Zustand des Magneten.
Die roten Kanten zeigen entgegengesetzt ausgerichtete Nachbarn. Jede rote Kante entspricht einer im Magneten gespeicherten Energiemenge, die genannt wird (dies steht hier nicht für die Energieeinheit Joule, sondern für eine Kenngröße des jeweiligen Materials).
Jede rote Kante vermindert die Wahrscheinlichkeit, den Zustand in der Natur anzutreffen, und zwar umso mehr, je kälter es ist. Man berechnet dies, indem man die Wahrscheinlichkeit für den Zustand „alle Atome gleichgerichtet“ für jede rote Kante einmal mit multipliziert. Dabei ist der Nenner das Produkt aus der Temperatur in Kelvin und der Boltzmann-Konstanten.
Beispiel: An einem warmen Sommertag (27 Grad Celsius, d. h. ca. 300 K) bewirkt in einem Material, dessen -Wert 0,0595 Elektronenvolt beträgt, jede rote Kante eine Wahrscheinlichkeitsminderung um den Faktor 10. Bei Abkühlung auf minus 123 Grad Celsius, d. h. ca. 150 K, ist der Faktor schon 100 und bei minus 173 Grad, d. h. ca. 100 K, sogar 1000.
Das Gesagte betrifft die Wahrscheinlichkeit eines individuellen Zustandes, die meist sehr klein ist. Meist gibt es aber auch eine sehr große Zahl von Zuständen, die eine bestimmte Magnetisierungsstärke des Magneten (Anzahl schwarzer Quadrate minus Anzahl weißer Quadrate) herstellen (man denke an die zahlreichen Möglichkeiten, einen Lottoschein auszufüllen).
Die große Zahl von Zuständen kann die kleine Wahrscheinlichkeit des einzelnen Zustandes ausgleichen. Tatsächlich gibt es in der Regel bei gegebener Temperatur eine bestimmte Magnetisierungsstärke, die alle anderen an Wahrscheinlichkeit deutlich übertrifft. Diese Magnetisierung wird fast ausschließlich angetroffen. Mit zunehmender Temperatur verschiebt sie sich von „voll magnetisiert“ zu „entmagnetisiert“.
Extreme Temperaturen[Bearbeiten | Quelltext bearbeiten]
Um ein Gefühl für die Bedeutung des oben gesagten zu finden, betrachte man zuerst die Grenzfälle sehr geringer und sehr hoher Temperatur. Entgegen der Intuition werden die Berechnungen dabei nicht etwa durch große Zahlen erschwert, sondern so einfach, dass man schon durch „Kopfrechnung“ zu Ergebnissen kommt.
Bei extrem tiefen Temperaturen (Temperatur nähert sich dem absoluten Nullpunkt) wird der Wahrscheinlichkeitsfaktor so klein, dass kein Zustand außer „alle schwarz“ oder „alle weiß“ jemals angetroffen werden kann. Der Magnet nimmt somit seine volle Magnetisierung an.
Bei extrem hohen Temperaturen hingegen wird der Wahrscheinlichkeitsfaktor der Zahl 1 immer ähnlicher, so dass er zu keiner Wahrscheinlichkeitsminderung führt und alle Zustände gleich wahrscheinlich werden. Dann gilt für jede Magnetisierung die reine Anzahl der sie realisierenden Zustände, und die ist für „50 % weiß – 50 % schwarz“ am höchsten. Der Magnet ist effektiv entmagnetisiert.
Moderate Temperatur[Bearbeiten | Quelltext bearbeiten]

Der abgebildete Zustand mit einem abweichenden Atom weist vier rote Kanten auf. Bei einem -Wert von 0,0017 eV ist dieser eine Zustand zehnmal weniger wahrscheinlich als die Vollmagnetisierung (bei 27 Grad Celsius). Allerdings gibt es 25 Möglichkeiten, genau ein Atom abweichen zu lassen, und so ist eine Magnetisierung von 24 Einheiten (25 – 1 entgegengesetzt) 2,5-mal so wahrscheinlich wie die Vollmagnetisierung.
Kritische Temperatur[Bearbeiten | Quelltext bearbeiten]
Der Zusammenbruch des Magnetismus tritt schon bei einer endlichen Temperatur auf, der kritischen Temperatur . Dies zu begründen erfordert umfangreiche mathematische Analysen, die hier nicht ausgeführt werden können.
Nahe der kritischen Temperatur treten „interessante“ Muster (bezüglich der Schwarz-Weiß-Verteilung) auf.
Strukturbildung[Bearbeiten | Quelltext bearbeiten]


Auf dem Weg vom absoluten Nullpunkt zu unendlicher Temperatur gelangt man von perfekter Ordnung zu perfektem Rauschen.
Dazwischen findet man „interessante“ Muster. Bezüglich des Magnetisierungswertes bildet sich ein Kompromiss zwischen geringer Wahrscheinlichkeit und großer Anzahl eines Zustands: Eine beliebig herausgegriffene kompakte Struktur weist zwar weniger rote Kanten auf (und ist daher wahrscheinlicher) als eine beliebig herausgegriffene aufgelockerte Struktur; weil es aber mehr aufgelockerte Strukturen gibt, kann die Eigenschaft „aufgelockert“ insgesamt wahrscheinlicher sein. Man wird also einen Kompromiss vorfinden, der weder ganz kompakt noch ganz zerrissen ist, eben eine „interessante“ Struktur.
Analog kann man argumentieren bezüglich der Streuung schwarzer und weißer Quadrate, wenn Temperatur und Magnetisierung gegeben sind.
Anwendungen und Interpretationen[Bearbeiten | Quelltext bearbeiten]
Die ursprüngliche Interpretation des Isingmodells ist die „magnetische“: Die Spinwerte zeigen nach „oben“ bzw. nach „unten“. Aber auch für andere binäre Probleme bietet sich das Isingmodell an.
Ein prominentes Beispiel ist das „Ising-Gittergas“, das zur Modellierung von Flüssigkeiten benutzt werden kann: Man betrachtet hierbei ein Gitter, dessen Plätze entweder „besetzt“ oder „unbesetzt“ sein können, je nachdem, ob der dem Gitterplatz zugeordnete Isingspin den Wert +1 oder −1 hat.
Mit dem Isingmodell können auch Spingläser beschrieben werden, nämlich mit der Energie , wobei die -Variablen die Ising-Spins bedeuten und die feste, aber zufällige Werte annehmen.
Quantenchromodynamik[Bearbeiten | Quelltext bearbeiten]
Darüber hinaus existiert eine Interpretation dieses Hamiltonoperators als ein stark vereinfachtes Modell der Quantenchromodynamik in der Elementarteilchenphysik: Man kann die -Variablen als Quarks und die als Gluonen interpretieren, wenn man beide Größen fluktuieren lässt. Allerdings muss man in diesem Fall zum Hamiltonoperator noch die als Wilson-Loop-Variablen bezeichneten Gluon-Gluon-Kopplungen der Form hinzufügen.
Man erhält dann eichinvariante Modelle, welche mit unkorrelierten binären Größen und den gekoppelten Eichtransformationen , , genügen; d. h. der Hamiltonoperator bleibt bei diesen Transformationen invariant, so wie die Lagrangefunktion der Quantenchromodynamik gegenüber Transformationen mit den Elementen der Gruppe SU(3) invariant bleibt, die hier durch die -Variablen ersetzt sind.
Mit diesem Modell – einer Art Ising Lattice QCD – wurde die Gittereichtheorie eingeführt. Die relevante Veröffentlichung dazu stammt von Franz Wegner. [10]
Nukleation[Bearbeiten | Quelltext bearbeiten]

Eine weitere Anwendungsmöglichkeit ist die Simulation von Phasenübergängen durch Nukleation. Homogene Nukleation entspricht bei der Modellierung ziemlich exakt dem Ferromagnetismus, für heterogene Nukleation müssen einige kleine Änderungen vorgenommen werden.
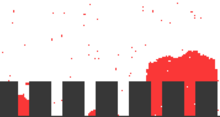
Die erste Summe ist in diesem Fall wieder die Interaktion zwischen Nachbarn, die neu hinzugekommene zweite Summation über steht jedoch für die Interaktion mit einer Begrenzungsfläche.[13] Es zeigt sich, dass im Bereich derartiger Begrenzungsflächen ein Kern kritischer Größe um ein Vielfaches schneller entsteht.
Basierend darauf wurden auch Simulationen zur Nukleation auf poröser Oberfläche durchgeführt. Ihr Ergebnis war, dass eine bestimmte Größe der Poren gegeben sein muss, um schnellstmögliche Nukleation zu gewährleisten (in der Regel ist dies bei unregelmäßigen Poren am ehesten gegeben): Bei großen Poren ist der Anteil an Begrenzungsflächen kleiner, dadurch entsteht länger kein Nukleationskern kritischer Größe in der Pore; wenn die Pore hingegen klein ist, so ist die Initiation eines Phasenübergangs vom oberen Rand weg weniger wahrscheinlich.[14]
Einzelnachweise und Fußnoten[Bearbeiten | Quelltext bearbeiten]
- ↑ E. Ising, Beitrag zur Theorie des Ferromagnetismus, Zeitschrift für Physik, Band 31, 1925, S. 253–258
- ↑ Bezüglich der Mitnahme des Faktors 1/2 gibt es unterschiedliche Konventionen (oft wird er fortgelassen)
- ↑ W.Selke: The ANNNI model. In: Physics Reports 170, 1988, S. 213–264, doi:10.1016/0370-1573(88)90140-8
- ↑ R.Peierls, Ising’s model of ferromagnetism, Proc. Cambridge Phil. Soc., Band 32, 1936, S. 477–481
- ↑ H.A.Kramers, G.Wannier, Statistics of the two dimensional Ferromagnet, 2 Teile, Phys. Rev., Band 60, 1941, S. 252–262, 263–276
- ↑ L.Onsager, Crystal Statistics I, Physical Review, Band 65, 1944, S. 117–149
- ↑ C. N. Yang, The spontaneous magnetization of the two dimensional Ising model, Phys. Rev., Band 85, 1952, S. 808–816
- ↑ M. Kac, J.C. Ward, Physical Review Bd. 88, 1952, S. 1332
- ↑ T.D. Schultz, E. Lieb, D.C. Mattis, Two dimensional Ising model as a soluble model of many fermions, Rev. Mod. Phys., Band 36, Juli 1964, S. 856–871
- ↑ F. Wegner, Duality in Generalized Ising Models and Phase Transitions without Local Order Parameter, J. Math. Phys. 12 (1971) 2259-2272. Reprinted in Claudio Rebbi (ed.), Lattice Gauge Theories and Monte Carlo Simulations, World Scientific, Singapore (1983), S. 60–73. (Abstract)
- ↑ A. J. Page, R. P. Sear: Heterogeneous nucleation in and out of pores. In: Physical review letters. Band 97, Nummer 6, August 2006, S. 065701, doi:10.1103/PhysRevLett.97.065701, PMID 17026175. (Variablennamen und Vorzeichen angepasst um Konsistenz auf der Seite zu gewährleisten)
- ↑ Berechnet mit GitHub
- ↑ Sofern die Begrenzungsfläche Nukleation nicht direkt begünstigt (), ist die einzige Änderung, die man für die derart geänderte Hamiltonfunktion durchführen muss, den Spin aller Atome, die zur Wand gehören, auf 0 zu ändern.
- ↑ D.Frenkel: Physical chemistry: Seeds of phase change. In: Nature. 443, 2006, S. 641, doi:10.1038/443641a.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Barry Cipra: An introduction to the Ising model, American Mathematical Monthly, Band 94, 1987, S. 937–959, pdf
- Barry McCoy, Tai Tsun Wu: The two dimensional Ising model, Harvard University Press 1973
- John Kogut: An introduction to lattice gauge theory and spin systems, Rev. Mod. Phys., Band 51, 1979, S. 659–713
- Richard Feynman: Statistical mechanics, Benjamin 1972
- Kerson Huang: Statistical mechanics, Wiley 1987
- Stephen G. Brush: History of the Lenz-Ising model, Rev. Mod. Phys., Band 39, 1967, S. 883–893


































