Kettenlinie (Mathematik)

Eine Kettenlinie (auch Seilkurve, Katenoide oder Kettenkurve, englisch catenary oder funicular curve) ist eine mathematische Kurve, die den Durchhang einer an ihren Enden aufgehängten Kette unter dem Einfluss der Schwerkraft beschreibt. Es handelt sich um eine elementare mathematische Funktion, den Cosinus hyperbolicus, kurz cosh.
Mathematische Beschreibung[Bearbeiten | Quelltext bearbeiten]
Erste Herleitung: Minimum der potentiellen Energie[Bearbeiten | Quelltext bearbeiten]
Die Berechnung der Kettenlinie ist ein klassisches Problem der Variationsrechnung. Man denkt sich ein Seil von gewisser Masse und Länge, das an seinen Enden aufgehängt ist. Die Seilkurve ist das Ergebnis der kleinstmöglichen potentiellen Energie des Seils. Das versucht man rechnerisch nachzuvollziehen.
Dazu benötigt man den mathematischen Ausdruck für die potentielle Energie. Er ist eine Verfeinerung des bekannten „Gewicht mal Höhe“ . Die Verfeinerung besteht darin, dass die Energie für „alle Teile“ des Seils getrennt ausgewertet und zum Schluss summiert wird. Das ist notwendig, weil die Teile des Seils sich auf unterschiedlichen Höhen befinden. Die gedankliche Zerlegung des Seils in immer kleinere Teile macht aus der Summe ein Integral. Die Höhe aus wird durch die gesuchte Funktion ersetzt, die Masse durch die Masse des Seilstücks über dem Intervall ; nach Pythagoras ist dies:
wobei die Masse je Meter ist. Wenn das Seil an den Stellen , aufgehängt ist, ergibt sich demnach die Energie („Gewicht mal Höhe“) als
Eine ähnliche Überlegung führt auf den Ausdruck für die Länge des Seils:
Die Energie ist zu minimieren, die Länge ist jedoch vorgegeben. Man bringt dies unter einen Hut durch einen Lagrange-Multiplikator , das heißt, man minimiert nun den Ausdruck
Die Variation ergibt die Differentialgleichung (Euler-Lagrange-Gleichung):
Interessanterweise sind in diesem Schritt sowohl die Massengröße als auch die Schwerebeschleunigung herausgefallen. Ein schweres Seil nimmt somit dieselbe Form an wie ein leichtes, und auf dem Mond ergibt sich trotz anderer Fallbeschleunigung dieselbe Form wie auf der Erde.
Die Lösungen der Gleichung sind die Funktionen
Es handelt sich um vergrößerte und verschobene Cosinus-hyperbolicus-Funktionen. ist der Krümmungsradius im Scheitelpunkt (siehe Abbildung) und zugleich der Vergrößerungsfaktor. ist die Verschiebung in -Richtung, die Verschiebung in -Richtung.
Die konkrete Form, die das Seil letztendlich annimmt, errechnet man, indem man , und so anpasst, dass die Kurve durch die Aufhängepunkte geht und die vorgegebene Länge hat.
Zweite Herleitung: Kräfteparallelogramm[Bearbeiten | Quelltext bearbeiten]
Bei einem Gewichtstück, welches über zwei Halteseile S1 und S2 mit den Steigungen t1 und t2 an insgesamt zwei Säulen aufgehängt ist, werden die Kräfte an den Seilen durch ein Kräfteparallelogramm mit der Haltekraft FH als Diagonale beschrieben. Der Vektor der Haltekraft FH bildet zum Vektor der Gewichtskraft FG den betragsgleichen Gegenvektor. Das Parallelogramm wird durch den Haltekraftvektor in zwei zueinander kongruente Dreiecke aufgeteilt. Mit dem Sinussatz können die Beträge der zwei Zugkräfte an den Seilen FS1 und FS2 berechnet werden:
Bei zwei gleich schweren Gewichtstücken, welche jeweils mit einem Halteseil an ihre zugehörige Säule aufgehängt und mit einem anderen gemeinsamen Halteseil SM zueinander verknüpft sind, gilt wegen des Kräftegleichgewichts im mittleren gemeinsamen Seil folgende Gesetzmäßigkeit:
Dabei ist tL die Steigung vom Seil SL, tM ist die Steigung vom Seil SM und tR ist die Steigung vom Seil SR.
Bei einer Kette aus insgesamt m Seilen und m - 1 gleich schweren Gewichtstücken zwischen den Seilen hat die Differenz von der Steigung eines Seils minus die Steigung des vorgängerischen Seils immer denselben Wert:
Durch die Gleichsetzung aller Seillängen und die Annäherung der Seillängen gegen Null entwickelt sich als Grenzwert m gegen Unendlich die Kette zu einer idealen Kettenkurve. Somit ist bei einer idealen Kettenkurve die Steigung der Kurve linear zur Kurvenlänge. Die Steigung ist also direkt proportional zum Bogenmaß angesetzt am relativen Minimum der Kurve. Diejenige Funktion, welche in ihrem Graph diese direkte Proportionalität zwischen Kurvensteigung und Kurvenlänge aufweist, ist der Cosinus Hyperbolicus. Bei folgender Differentialgleichung wird die Kurvenlänge als Integral des pythagoräischen Nachfolgers der Ableitung und die Steigung als Ableitung selbst angegeben:
Länge[Bearbeiten | Quelltext bearbeiten]
Ist die Kettenkurve als Gleichung gegeben und verläuft sie durch die Aufhängepunkte und , dann gilt für die Höhendifferenz der Punkte:
und für die Länge zwischen den Aufhängepunkten der Kettenkurve gilt:
Für die Herleitung wurden die Ableitungsfunktion und Stammfunktion von Sinus hyperbolicus und Kosinus hyperbolicus und die Gleichung verwendet. Aus den zwei hergeleiteten Gleichungen und dem Additionstheoremen und folgt:
Beispiele[Bearbeiten | Quelltext bearbeiten]

Beispiel 1[Bearbeiten | Quelltext bearbeiten]
Als Beispiel sei ein zwischen zwei Pfosten (Abstand ) aufgehängtes Seil der Länge gegeben (siehe Abbildung). Die Pfosten sind gleich hoch und befinden sich bei und , es gilt also .
Um den Krümmungsradius zu berechnen, schreiben wir die Seillänge als Funktion von :
- .
Diese Beziehung legt in Abhängigkeit von und eindeutig fest. Da man keinen geschlossenen Ausdruck für angeben kann, muss der Wert mit einem numerischen Verfahren zur Lösung nichtlinearer Gleichungen approximativ berechnet werden.
Sind jedoch und gegeben, können und wie folgt geschlossen dargestellt werden.
Wird das Quadrat aus der Gleichung (oben) vom Quadrat aus der (unten erwähnten) Gleichung subtrahiert, dann ergibt die mit der Differenz entstehende Gleichung , woraus wegen eliminiert und nach umgestellt werden kann.
Einsetzen dieses in und Umformungen ergeben den gesuchten Ausdruck für den Abstand in geschlossener Form z. B.
oder
- .
Zuletzt liest man aus der Abbildung die Bedingung ab, aus der man erhält. Des Weiteren gelten die Beziehungen
wobei der „Durchhang“ ist.
Die potentielle Energie dieses Systems beträgt
- .
Genauer ist dies die Energiedifferenz gegenüber dem Fall, dass sich das Seil komplett auf der Höhe der Aufhängepunkte () befindet.

Mit Hilfe der Energie kann man die Kraft in den Aufhängepunkten berechnen. Hierzu stellt man sich vor, dass das Seil in einem Aufhängepunkt über eine Umlenkrolle läuft, die die Kraft in horizontale Richtung umlenkt. Um das Seil wie abgebildet um eine sehr kleine Strecke hinauszuziehen, muss man die Energie aufwenden. Diese kann man berechnen und erhält so die Kraft . Zur Berechnung von vergleicht man die Energie des ursprünglichen Seils mit der des um verkürzten Seiles. Das Ergebnis ist überraschend einfach, nämlich
mit . Dieselbe Formel kann man auch auf Teilstücke des Seils anwenden. Da die Teilstücke alle denselben Krümmungsradius haben, aber für kleine Teilstücke (unten im Tal) der Durchhang vernachlässigbar wird, besteht im Tal des Seiles die Seilspannung .
Stellt man die Pfosten nah beisammen, dann dominiert der Durchhang , der dann recht genau die halbe Seillänge ist. Die Kraft ist dann erwartungsgemäß die halbe Gewichtskraft des Seiles, (man beachte, dass zwei Aufhängepunkte sich die Last teilen).
Die Formel zeigt auch, wie die Kraft bei zunehmender Seilspannung die halbe Gewichtskraft um den Faktor übersteigt. Der Faktor ist praktisch 1 für sehr kleine Krümmungsradien , aber ungefähr oder auch für sehr große Krümmungsradien.
Im Alltag beträgt der Faktor etwa 2 bis 4. Im Aufhängepunkt wirkt dann das ganze oder doppelte Gewicht des Seiles.
Beispiel 2[Bearbeiten | Quelltext bearbeiten]
Für = 100 m und einen Mastabstand von 200 m (also Spezialfall ) wird ein 2·117,5 m langes Seil benötigt: . Der Durchhang beträgt 54 m. Für ein Stahlseil mit 100 cm² Querschnitt wiegt eine Seilhälfte 9,2 t. Die entsprechende Gewichtskraft von 9·104 N ist die vertikale Kraft an einer Aufhängung. Die horizontale Kraft an einer Aufhängung beträgt 7,7·104 N.
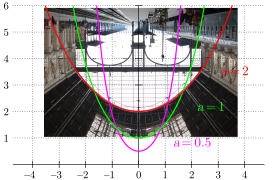
Beträgt etwa 20,2 % der gesamten Breite , so ist der Durchhang Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „http://localhost:6011/de.wikipedia.org/v1/“:): {\displaystyle y(x=w/2)} gleich der Breite (quadratförmige Gesamtabmessungen). Dieser Fall liegt beispielsweise vor beim Gateway Arch (siehe unten im Abschnitt Architektur), der 630 Fuß breit und ebenso hoch ist. Die exakte Formel
mit a = 127,7 Fuß und w/2 = 315 Fuß ist im Inneren des Denkmals ausgestellt. Gleichwohl bildet das Bauwerk aufgrund der variierenden Bogenstärke streng genommen keine Kettenlinie.
Beispiel 3[Bearbeiten | Quelltext bearbeiten]
Zwei Säulen der Höhen g = 1 m und h = 2 m stehen in einem Abstand von d = 3 m voneinander entfernt.
Zwischen ihnen wird eine Kette der Länge k = 4 m aufgehängt.
| Frage 1:
Wie groß ist der Krümmungsradius a von dieser Kettenkurve? Synthese der Formeln: Unter der Annahme, dass sich bei der Eintragung in ein Koordinatensystem die Spitze der Säule g als Anfang der Kette am Punkt (0,g) und Spitze der Säule h als Ende der Kette am Punkt (d,h) befindet, gilt folgendes Gleichungssystem:
Die Höhendifferenz der Kette werden durch die Cosinus-Hyperbolicus-Differenz beschrieben. Die Kettenlänge wird durch die Sinus-Hyperbolicus-Differenz beschrieben. Die Theoreme der Hyperbelfunktionen ermöglichen die Umwandlungen von Summen zu Produkten:
Mit dem Additionstheorem des Cosinus Hyperbolicus entsteht aus der Kombination II² - I² folgende vom Parameter befreite Formel:
Mit dieser Formel kann der Wert von a direkt berechnet werden. Einsatz der Werte: Durch das Einsetzen der genannten Werte für g, h, d, und k entsteht dieser Wert für a: Werte: g = 1 m, h = 2 m, d = 3 m, k = 4 m Ermittlung des Krümmungsradius:
Antwort: Der Krümmungsradius dieser Kettenkurve beträgt 1,182 m. |
| Frage 2:
Wie weit ist der Scheitelpunkt von der Säule g entfernt? Synthese der Formeln: Diese Formeln kommen aus der Bearbeitung der ersten Teilfrage:
Durch die Rechnung I/II und anschließende Auflösung nach entsteht diese Formel:
Einsatz der Werte: Ermittlung der Distanz des Scheitelpunkts zur Säule g:
Antwort: Der Scheitelpunkt ist 1,198 m von der Säule g entfernt. |
| Frage 3:
Wie hoch steht der Scheitelpunkt? Synthese der Formeln: Es gilt die generelle Kettengleichung: Wenn der Wert eingesetzt wird, dann komm diese Gleichung hervor: Diese Gleichung wird nach dem Ordinatenverschiebungswert aufgelöst: Und jene Formel gilt direkt für den gesuchten Scheitelpunkt durch Einsetzen des Wertes : Folgende Formel führt direkt zur Höhe des Scheitelpunktes:
Einsatz der Werte: Die Werte g, a und werden in die Gleichung V eingesetzt:
Antwort: Der Scheitelpunkt steht 0,339 m hoch. |
Beziehungen zu anderen Funktionen[Bearbeiten | Quelltext bearbeiten]
Parabel[Bearbeiten | Quelltext bearbeiten]

Joachim Junge wies 1639 nach, dass die Kettenlinie keine Parabel ist. Gottfried Leibniz, Christiaan Huygens und Johann I Bernoulli fanden 1690/91 heraus, wie die Kettenkurve zu bilden ist.[1] Wenn man die Reihenentwicklung der Kettenlinie betrachtet, erkennt man, dass es sich dabei um eine unendliche Summe von Termen ganzrationaler Funktionen geradzahligen Grades handelt:
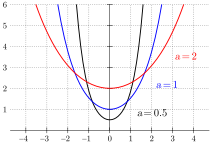
Für hinreichend kleine Beträge von kann man die Reihe nach dem zweiten Glied abbrechen und erhält dann als Näherungskurve im Bereich des Scheitelpunktes eine quadratische Parabel, die indes (außer im Scheitelpunkt selbst) immer „unterhalb“ der eigentlichen Kettenlinie liegt, d. h. zu kleine Werte liefert.
Eine quadratische Parabel stellt sich hingegen ein bei einer gleichmäßig über die Spannweite verteilten Streckenlast, z. B. einer Hängebrücke, sofern das Gewicht der Seile gegenüber dem der Fahrbahn vernachlässigt werden kann. (Wenn diese letztere Bedingung nicht erfüllt ist und also die Tragseile einen wesentlichen Teil des Gesamtgewichts ausmachen, ist die Berechnung der Seilkurve in Form einer geschlossenen Funktion nicht möglich.).
Die Abbildung rechts vergleicht den Kurvenverlauf einer Kettenlinie (rot) mit dem einer Normalparabel (grün).

m(0)=1/2, c(0)=2: Der unbestimmte Ausdruck 0/0 ist in diesem Fall 1/2 bzw. 2.
Katenoid[Bearbeiten | Quelltext bearbeiten]
Die durch Rotation der Kettenlinie um die x-Achse erzeugte Rotationsfläche wird als Katenoid bezeichnet und ist neben der Ebene die einzige Rotationsfläche, die auch eine Minimalfläche ist: Katenoide sind statisch gesehen als ideale Dachformen für Rundtürme anzusehen, da sie sich (theoretisch) selbst tragen.
Hält man zwei Ringe nebeneinander und taucht sie in eine Seifenlösung, um sie mit einer Seifenhaut zu überziehen, so bildet sich ein Katenoid zwischen den Ringen aus.
Traktrix[Bearbeiten | Quelltext bearbeiten]
Die Kettenlinie ist die Evolute zu der Traktrix (Schleppkurve).
Anwendungen in der Architektur[Bearbeiten | Quelltext bearbeiten]
Einer der Kettenlinie analogen Stützlinie folgt der scherkräftefreie Bogen:
- Die Nubische Tonne, ein Tonnengewölbe, ist eine Variante des Nubischen Gewölbes, einer Gewölbebauweise im Lehmbau ohne Schalung und häufig ohne Lehren, die ihren Namen von traditionellen Bauformen in Nubien hat. Um die größtmögliche Stabilität zu erreichen, folgt die Stützlinie in der Regel der Kettenlinie.
- Ein frühes europäisches Beispiel ist die nach Plänen von Christopher Wren nach 1666 erbaute, im Durchmesser 30,80 m messende Kuppel der St Paul’s Cathedral in London.[2] Zwischen eine äußere und innere hölzerne Halbkugel ließ er ein Katenoid legen, das die Schwere der Laterne aufnahm, aber selbst ein geringeres Baugewicht ermöglichte. Die Kurve wurde damals noch empirisch angenähert.
- Auguste de Montferrand transformierte die Kuppel Wrens in der St. Paul’s Cathedral im Bau der Eisenkuppel der Isaakskathedrale in Sankt Petersburg (1838–1841) und nutzte mit Eisen ein neues Medium im Bau. Montferrands Eisenkuppel wurde selbst Vorbild für die Eisenkuppel des Kapitols in Washington (1855–1866).[3]
- Der Querschnitt des Daches des Bahnhofs Budapest Ost (Keleti) (Ungarn) bildet eine Kettenlinie. Erbaut von 1881/84. Konstrukteur: János Feketeházy.
- Antoni Gaudí nutzte häufiger das darauf fußende Konstruktionsprinzip, unter anderem bei der Sagrada Família in Barcelona. Das Modell der ähnlichen Kirche der Colònia Güell wurde ebenfalls empirisch ermittelt, nämlich „kopfüber“ durch hängende Schnüre mit entsprechenden Gewichten (um 1900; Original bei einem Brand verloren)
Fotos[Bearbeiten | Quelltext bearbeiten]
-
Experiment: stehende Kettenlinie
-
Bau eines Brennofens
-
Sheffield Winter Garden
-
Architekturmodell von Gaudí
-
Querschnitt des Daches des Ostbahnhofs in Budapest (Ungarn)
-
Variation des Parameters a, oder verschieden voneinander entfernte Aufhängungspunkte
-
Zeichnung von Christiaan Huygens
-
Die Seile von Freileitungen folgen der Kettenlinie
-
Spinnenfäden folgen ungefähr der Kettenlinie, hier durch Tautropfen betont
-
Drei Ketten umranden eine Kettenlinienfigur (analog zum Arbelos)
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Herleitung und Rechner
- Gesamtdarstellung des Themas Kettenlinie
- Die Kettenlinie Umfangreiche Darstellung mit interaktiver Grafik.





![{\displaystyle [x,x+\mathrm {d} x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2497bba0513a671ec5bbc5074589b01eb03b3374)

















![{\displaystyle |{\vec {F}}_{S1}|=|{\vec {F}}_{G}|\sin[{\tfrac {1}{2}}\pi -\arctan(t_{2})]\csc[\arctan(t_{2})-\arctan(t_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7596d821dd35da4dfddcff2ea30cf7e5852ef27f)
![{\displaystyle |{\vec {F}}_{S2}|=|{\vec {F}}_{G}|\sin[{\tfrac {1}{2}}\pi +\arctan(t_{1})]\csc[\arctan(t_{2})-\arctan(t_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec7b5af03f5693bf09f54ee4582d9f9f105fda9)
![{\displaystyle |{\vec {F}}_{G}|\sin[{\tfrac {1}{2}}\pi +\arctan(t_{L})]\csc[\arctan(t_{M})-\arctan(t_{L})]=|{\vec {F}}_{G}|\sin[{\tfrac {1}{2}}\pi -\arctan(t_{R})]\csc[\arctan(t_{R})-\arctan(t_{M})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7399fa828c4ba900de771da65d1af3a5075b6bbc)
![{\displaystyle \sin[{\tfrac {1}{2}}\pi +\arctan(t_{L})]\sin[\arctan(t_{R})-\arctan(t_{M})]=\sin[{\tfrac {1}{2}}\pi -\arctan(t_{R})]\sin[\arctan(t_{M})-\arctan(t_{L})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7502fd187451dece54e9de3f307e08955639b9b1)



![{\displaystyle \int _{x_{0}}^{x}{\sqrt {{\bigl [}{\frac {\mathrm {d} }{\mathrm {d} x}}y(x)(x=w){\bigr ]}^{2}+1}}\,\mathrm {d} w=a\,{\frac {\mathrm {d} }{\mathrm {d} x}}y(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cb843640d7e9c3cde7b75f2532a83dd6114aa71)
![{\displaystyle y(x)=a\cosh[(x-x_{0})/a]+y_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ceb00038d05460c9bf0c096449c90eb136bee135)










































![{\displaystyle h-g=a\cosh[(d-x_{\text{SP}})/a]-a\cosh(-x_{\text{SP}}/a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e49c51dd51a2b5bb8c450908a1e6e4d0cc8c051)
![{\displaystyle k=a\sinh[(d-x_{\text{SP}})/a]-a\sinh(-x_{\text{SP}}/a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c234a2ad862aa0fa30980c42737dbcad20d7807)









![{\displaystyle y(x)=a\cosh {\bigl [}(x-x_{SP})/a{\bigr ]}+y_{\text{VE}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c50852da14057e61047722c219ab6a998997cb)