Taylor-Formel

Die Taylor-Formel (auch Satz von Taylor) ist ein Resultat aus dem mathematischen Teilgebiet der Analysis. Sie ist benannt nach dem Mathematiker Brook Taylor. Man kann diese Formel verwenden, um Funktionen in der Umgebung eines Punktes durch Polynome, die sogenannten Taylorpolynome, anzunähern. Man spricht auch von der Taylor-Näherung. Die Taylor-Formel ist aufgrund ihrer relativ einfachen Anwendbarkeit und Nützlichkeit ein Hilfsmittel in vielen Ingenieur-, Sozial- und Naturwissenschaften geworden. So kann ein komplizierter analytischer Ausdruck durch ein Taylorpolynom geringen Grades (oftmals gut) angenähert werden, z. B. in der Physik oder bei der Ausgleichung geodätischer Netze: So ist die oft verwendete Kleinwinkelnäherung des Sinus eine nach dem ersten Glied abgebrochene Taylorreihe dieser Funktion.

Eng verwandt mit der Taylor-Formel ist die sogenannte Taylorreihe (Taylor-Entwicklung).

Motivation

Annäherung durch Tangente

Eine Näherung für eine differenzierbare Funktion $f$ an einer Stelle $a$ durch eine Gerade, also durch ein Polynom 1. Grades, ist gegeben durch die Tangente mit der Gleichung

$T_{1}f(x;a)=f(a)+f'(a)(x-a)$.

Sie lässt sich dadurch charakterisieren, dass an der Stelle $x=a$ die Funktionswerte und die Werte der 1. Ableitung (= Steigung) von $f(x)$ und $T_{1}f(x;a)$ übereinstimmen: $f(a)=T_{1}f(a;a),f'(a)=T_{1}'f(a;a)$.

Wenn man den Rest $R_{1}f(x;a):=f(x)-T_{1}f(x;a)$ definiert, so gilt $f(x)=T_{1}f(x;a)+R_{1}f(x;a)$. Die Funktion $T_{1}f(x;a)$ approximiert $f$ in der Nähe der Stelle $x=a$ in dem Sinne, dass für den Rest gilt

$(1)~\lim _{x\to a}{\frac {R_{1}f(x;a)}{x-a}}=\lim _{x\to a}{\frac {f(x)-T_{1}f(x;a)}{x-a}}=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}-f'(a)=0$ (siehe bei der Definition der Ableitung).

Annäherung durch Schmiegparabel

Man kann vermuten, dass man für zweimal differenzierbares $f$ eine noch bessere Näherung erhält, wenn man dazu ein quadratisches Polynom $T_{2}f(x;a)$ verwendet, von dem man verlangt, dass zusätzlich noch $T_{2}''f(a;a)=f''(a)$ gilt. Der Ansatz $T_{2}f(x;a)=a_{0}+a_{1}(x-a)+a_{2}(x-a)^{2}$ führt durch Berechnung der Ableitungen auf $a_{0}=f(a),a_{1}=f'(a)$ und $a_{2}={\frac {1}{2}}f''(a)$, also

$T_{2}f(x;a)=f(a)+f'(a)(x-a)+{\frac {1}{2}}f''(a)(x-a)^{2}$.

Diese Näherungsfunktion bezeichnet man auch als Schmiegparabel.

Man definiert nun dazu den passenden Rest $R_{2}f(x;a):=f(x)-T_{2}f(x;a)$, sodass wieder $f(x)=T_{2}f(x;a)+R_{2}f(x;a)$. Dann erhält man, dass die Schmiegparabel die gegebene Funktion bei $x=a$ in der Tat besser approximiert, da nun (mit der Regel von de l’Hospital):

$\lim _{x\to a}{\frac {R_{2}f(x;a)}{(x-a)^{2}}}=\lim _{x\to a}{\frac {f(x)-f(a)-f'(a)(x-a)}{(x-a)^{2}}}-{\frac {1}{2}}f''(a)=\lim _{x\to a}{\frac {f'(x)-f'(a)}{2(x-a)}}-{\frac {1}{2}}f''(a)=0$

gilt.

Annäherung durch Polynome vom Grad n

Dieses Vorgehen lässt sich nun leicht auf Polynome $n$-ten Grades $T_{n}(x)$ verallgemeinern: Hier soll gelten

$T_{n}f(a;a)=f(a),\ T_{n}'f(a;a)=f'(a),\ \ldots ,\ T_{n}^{(n)}f(a;a)=f^{(n)}(a)$.

Es ergibt sich

$T_{n}f(x;a)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dotsb +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}$.

Mit der Regel von de l’Hospital finden wir außerdem:

$\lim _{x\to a}{\frac {f(x)-T_{n}f(x;a)}{(x-a)^{n}}}=\lim _{x\to a}{\frac {f'(x)-T_{n}'f(x;a)}{n(x-a)^{n-1}}}$.

Daher ergibt sich mit vollständiger Induktion über $n$, dass für $R_{n}f(x;a)=f(x)-T_{n}f(x;a)$ gilt:

$\lim _{x\to a}{\frac {R_{n}f(x;a)}{(x-a)^{n}}}=0$.

Qualitative Taylorformel

Ist $f$ $n$-mal differenzierbar, so folgt sofort aus der obigen Betrachtung, dass

$f(x)=T_{n}f(x;a)+R_{n}f(x;a)=T_{n}f(x;a)+o(|x-a|^{n}),\quad x\rightarrow a,$

wobei $o$ für die Landau-Notation steht. Diese Formel nennt man „qualitative Taylorformel“.

Je näher $x$ bei $a$ liegt, desto besser approximiert also $T_{n}f(x;a)$ (das sog. Taylorpolynom, siehe unten) an der Stelle $x$ die Funktion $f$.

Definitionen und Satz

Im Folgenden wird die Taylor-Formel mit Integralrestglied vorgestellt. Die Taylor-Formel existiert auch in Varianten mit anderem Restglied; diese Formeln folgen jedoch aus der Taylor-Formel mit Integralrestglied. Sie stehen unten im Abschnitt Restgliedformeln.

Sei $I\subset \mathbb {R}$ ein Intervall und $f\colon I\to \mathbb {R}$ eine $(n+1)$-mal stetig differenzierbare Funktion. In den folgenden Formeln stehen $f',f'',\dots ,f^{(k)}$ für die erste, zweite, …, $k$-te Ableitung der Funktion $f$.

Taylorpolynom

Das $n$-te Taylorpolynom an der Entwicklungsstelle $a\in I$ ist definiert durch:

${\begin{aligned}T_{n}f(x;a)=&\sum _{k=0}^{n}{f^{(k)}(a) \over k!}(x-a)^{k}\\=&f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\ldots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\end{aligned}}$

Integralrestglied

Das $n$-te Integralrestglied ist definiert durch:

$R_{n}f(x;a)=\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t$

Satz (Taylorformel mit Integralrestglied)

Für alle $a$ und $x$ aus $I$ gilt:

${\begin{aligned}f(x)=&T_{n}f(x;a)+R_{n}f(x;a)\\=&\sum _{k=0}^{n}{f^{(k)}(a) \over k!}(x-a)^{k}+\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t\end{aligned}}$

Beweis

Der Beweis der Taylor-Formel mit Integralrestglied erfolgt durch vollständige Induktion über $n$.

Der Induktionsanfang $n=0$ entspricht dabei genau dem Fundamentalsatz der Analysis angewendet auf die einmal stetig differenzierbare Funktion $f$:

$f(x)=f(a)+\int \limits _{a}^{x}f'(t)\,\mathrm {d} t=T_{0}f(x;a)+R_{0}f(x;a)$

Der Induktionsschritt $n\rightarrow n+1$ (es ist zu zeigen, dass die Formel stets auch für $n+1$ gilt, falls sie für ein $n$ gilt) erfolgt durch partielle Integration. Für $(n+2)$-mal stetig differenzierbares $f$ ergibt sich:

${\begin{aligned}&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+R_{n+1}f(x;a)\\=&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+\int \limits _{a}^{x}{\frac {(x-t)^{n+1}}{(n+1)!}}f^{(n+2)}(t)\,\mathrm {d} t\\=&{\frac {f^{(n+1)}(a)}{(n+1)!}}(x-a)^{n+1}+\left[{\frac {(x-t)^{n+1}}{(n+1)!}}f^{(n+1)}(t)\right]_{t=a}^{t=x}-\int \limits _{a}^{x}{\frac {-(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t\\=&{\frac {(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}(a)-{\frac {(x-a)^{n+1}}{(n+1)!}}f^{(n+1)}(a)+R_{n}f(x;a)\\=&R_{n}f(x;a)\end{aligned}}$

und somit

$T_{n+1}f(x;a)+R_{n+1}f(x;a)=T_{n}f(x;a)+R_{n}f(x;a)=f(x)$.

Restgliedformeln

Es gibt außer der Integralformel noch andere Darstellungen des Restgliedes.

Schlömilch-Restglied und dessen Herleitung

Nach dem Mittelwertsatz der Integralrechnung ergibt sich für jede natürliche Zahl $p$ mit $1\leq p\leq n+1$, dass es ein $\xi$ zwischen $a$ und $x$ gibt, sodass:

$\int \limits _{a}^{x}{f^{(n+1)}(t){\frac {(x-t)^{n+1-p}}{n!}}\cdot (x-t)^{p-1}\,\mathrm {d} t}={\frac {f^{(n+1)}(\xi )(x-\xi )^{n+1-p}}{n!}}\cdot \underbrace {\int \limits _{a}^{x}{(x-t)^{p-1}\,\mathrm {d} t}} _{={\frac {(x-a)^{p}}{p}}}$

Damit folgt die Schlömilchsche Restgliedform:

$R_{n}f(x;a)=\int \limits _{a}^{x}{\frac {(x-t)^{n}}{n!}}f^{(n+1)}(t)\,\mathrm {d} t={\frac {f^{(n+1)}(\xi )}{p\cdot n!}}(x-\xi )^{n+1-p}(x-a)^{p}$

für ein $\xi$ zwischen $a$ und $x$.

Spezialfälle des Schlömilch-Restglieds

Ein Spezialfall, nämlich der mit $p=1$, ist die Form nach Cauchy:

$R_{n}f(x;a)={\frac {f^{(n+1)}(\xi )}{n!}}(x-\xi )^{n}(x-a)$

für ein $\xi$ zwischen $a$ und $x$.

Im Spezialfall $p=n+1$ erhalten wir das Lagrangesche Restglied:

$R_{n}f(x;a)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}$

für ein $\xi$ zwischen $a$ und $x$. Bei dieser Darstellung braucht die $(n+1)$-te Ableitung von $f$ nicht stetig zu sein.

Peano-Restglied

Mit der Taylorformel mit Lagrange-Restglied erhält man für $n$-mal stetig differenzierbares $f$ außerdem:

$f(x)=T_{n-1}f(x;a)+{\frac {f^{(n)}(\xi )}{n!}}(x-a)^{n}=T_{n}f(x;a)+{\frac {f^{(n)}(\xi )-f^{(n)}(a)}{n!}}(x-a)^{n}$

Darum kann man als Restglied auch

$R_{n}f(x;a)={\frac {f^{(n)}(\xi )-f^{(n)}(a)}{n!}}(x-a)^{n}$

verwenden, wobei $f$ hier nur $n$-mal stetig differenzierbar sein muss. Dieses Restglied nennt man Peano-Restglied.

Weitere Darstellung

Setzt man $\Theta ={\tfrac {\xi -a}{x-a}}$, das heißt $\xi =a+\Theta (x-a)$, so erhält die Lagrangesche Darstellung die Form

$R_{n}f(x;a)={\frac {f^{(n+1)}(a+\Theta (x-a))}{(n+1)!}}(x-a)^{n+1}$,

die Schlömilchsche

$R_{n}f(x;a)={\frac {f^{(n+1)}(a+\Theta (x-a))}{p\cdot n!}}(1-\Theta )^{n+1-p}(x-a)^{n+1}$,

und die Cauchysche

$R_{n}f(x;a)={\frac {f^{(n+1)}(a+\Theta (x-a))}{n!}}(1-\Theta )^{n}(x-a)^{n+1}$

jeweils für ein $\Theta$ zwischen 0 und 1.

Restgliedabschätzung

Liegt das Intervall $(a-r,a+r)$ in $I$ (der Definitionsbereich von $f$), kann man mit dem Restglied von Lagrange (siehe im Abschnitt Restgliedformeln) für alle $x\in (a-r,a+r)$ und ein $\xi$ zwischen $a$ und $x$ (und somit auch $\xi \in (a-r,a+r)$) folgende Abschätzung herleiten:

$|R_{n}f(x;a)|=\left|{\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}\right|\leq \sup _{\xi \in (a-r,a+r)}\left|{\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}\right|$

Gilt $|f^{(n+1)}(x)|\leq M_{n}$ für alle $x\in (a-r,a+r)$, so gilt daher für das Restglied die Abschätzung

$\forall x\in (a-r,a+r):|R_{n}f(x;a)|\leq M_{n}{\frac {|x-a|^{n+1}}{(n+1)!}}\leq M_{n}{\frac {r^{n+1}}{(n+1)!}}$.

Näherungsformeln für Sinus und Kosinus

Eine Anwendung der Taylorformel sind Näherungsformeln, hier vorgestellt am Beispiel Sinus und Kosinus (wobei das Argument im Bogenmaß angegeben wird).

Für $f(x)=\sin(x)$ gilt $f'(x)=\cos(x),\,f''(x)=-\sin(x),\,f'''(x)=-\cos(x),f''''(x)=\sin(x)$, also lautet das 4. Taylorpolynom der Sinusfunktion an der Entwicklungsstelle 0

$T_{4}\sin(x;0)=f(0)+f'(0)x+{\frac {1}{2}}f''(0)x^{2}+{\frac {1}{6}}f'''(0)x^{3}+{\frac {1}{24}}f''''(0)x^{4}=x-{\frac {x^{3}}{6}}.$

Aus $f^{(5)}(x)=\cos(x)$ ergibt sich für das Restglied von Lagrange $R_{4}\sin(x;0)={\frac {f^{(5)}(\xi )}{5!}}x^{5}={\frac {\cos(\xi )}{120}}x^{5}$ mit $\xi$ zwischen 0 und $x$. Wegen $|\cos(\xi )|\leq 1$ folgt die Restgliedabschätzung $|T_{4}\sin(x;0)-\sin(x)|\leq {\frac {|x|^{5}}{120}}$.

Liegt $x$ zwischen $-{\frac {\pi }{4}}$ und ${\frac {\pi }{4}}$, dann liegt die relative Abweichung $\left|{\frac {T_{4}\sin(x;0)-\sin(x)}{\sin(x)}}\right|$ von $T_{3}\sin(x;0)$ zu $\sin(x)$ bei unter 0,5 %.

Tatsächlich genügt für die Annäherung des Sinus auf diese Genauigkeit sogar schon das Taylorpolynom 3. Ordnung, da $f''''(0)=0$ für $f(x)=\sin(x)$, und daher $T_{3}\sin(x;0)=T_{4}\sin(x;0)$. Daraus ergibt sich auch folgende weitere Abschätzung für drittes und viertes Taylorpolynom, die bei sehr großen x genauer ist:

$|T_{4}\sin(x;0)-\sin(x)|\leq {\frac {x^{4}}{24}}$

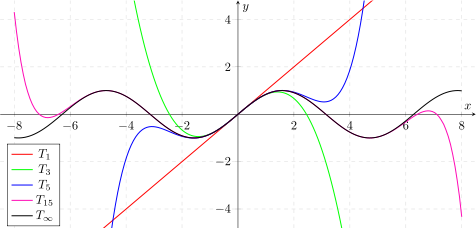
Die folgende Abbildung zeigt die Graphen einiger Taylorpolynome des Sinus um Entwicklungsstelle 0 für $n=1,3,5,15$. Der Graph zu $n=\infty$ gehört zur Taylorreihe, die mit der Sinusfunktion übereinstimmt.

Approximation des Sinus durch Taylorpolynome $T_{1}\sin(x;0)$ bis $T_{81}\sin(x;0)$

Das vierte Taylorpolynom $T_{4}\cos(x;0)$ der Kosinusfunktion an der Entwicklungsstelle 0 hat im Horner-Schema diese Gestalt:

$\cos(x)\approx T_{4}\cos(x;0)=\left({\frac {x^{2}}{12}}-1\right)\cdot {\frac {x^{2}}{2}}+1$

Liegt x zwischen $-{\frac {\pi }{4}}$ und ${\frac {\pi }{4}}$, dann liegt die relative Abweichung $\left|{\frac {T_{4}\cos(x;0)-\cos(x)}{\cos(x)}}\right|$ bei unter 0,05 %.

Auch für Kotangens und Tangens kann man diese Formeln nutzen, denn es ist

$\tan(x)\sim t(x)={\frac {T_{3}\sin(x;0)}{T_{4}\cos(x;0)}}$

mit einer relativen Abweichung von unter 0,5 % für $\left|x\right|<{\frac {\pi }{4}}$, und $\cot(x)\sim 1/t(x)$ mit derselben relativen Abweichung (dabei ist $t$ kein Taylorpolynom des Tangens).

Braucht man eine noch höhere Genauigkeit für seine Näherungsformeln, dann kann man auf höhere Taylorpolynome zurückgreifen, die die Funktionen noch besser approximieren.

Taylor-Formel im Mehrdimensionalen

Siehe auch: „Mehrdimensionale Taylorreihe“ im Artikel Taylorreihe

Sei nun im Folgenden $f\colon \mathbb {R} ^{d}\to \mathbb {R}$ eine $n+1$-mal stetig differenzierbare Funktion und $x=(x_{1},\ldots ,x_{d}),a=(a_{1},\ldots ,a_{d})\in \mathbb {R} ^{d}$. Sei ferner $F\colon \mathbb {R} \to \mathbb {R}$, $F(t)=f(a+th)$, wobei $h=x-a$.

Sei ferner wie in der Multiindex-Notation $D^{\alpha }={\frac {\partial ^{|\alpha |}}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{d}^{\alpha _{d}}}}$. Im folgenden Abschnitt wird die Multiindex-Notation verwendet, damit man sofort sieht, dass der mehrdimensionale Fall für $d=1$ tatsächlich dieselben Formeln ergibt wie der eindimensionale Fall.

Mehrdimensionales Taylorpolynom

Mit der mehrdimensionalen Kettenregel und Induktion erhält man, dass

$F^{(n)}(t)=\sum _{|\alpha |=n}\left({\begin{matrix}n\\\alpha \end{matrix}}\right)(x-a)^{\alpha }D^{\alpha }f(a+th)$,

wobei $\left({\begin{matrix}n\\\alpha \end{matrix}}\right)$ der Multinomialkoeffizient ist, siehe Multinomialtheorem.

Stellt man $F$ im Punkt 1 durch ein Taylorpolynom mit Entwicklungsstelle 0 dar, so erhält man durch diese Formel die Definition des mehrdimensionalen Taylorpolynoms von $f$ an der Entwicklungsstelle $a$:

$T_{n}f(x;a):=T_{n}F(1;0)=\sum _{|\alpha |=0}^{n}{\frac {(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a)$

Hierbei hat man verwendet, dass $\left({\begin{matrix}n\\\alpha \end{matrix}}\right)\cdot {\frac {1}{n!}}={\frac {1}{\alpha !}}$.

Schmiegquadrik

Das zweite Taylorpolynom einer skalarwertigen Funktion in mehr als einer Variable kann bis zur zweiten Ordnung kompakter geschrieben werden als:

$T_{2}f(x;a)=f(a)+\nabla f(a)^{T}(x-a)+{\frac {1}{2}}(x-a)^{T}\operatorname {H} _{f}(a)(x-a)$

Dabei ist $\nabla f(a)$ der Gradient und $\operatorname {H} _{f}(a)$ die Hesse-Matrix von $f$ jeweils an der Stelle $a$.

Das zweite Taylorpolynom nennt man auch Schmiegquadrik.

Mehrdimensionales Integralrestglied

Ebenso definiert man das mehrdimensionale Restglied mithilfe der Multiindex-Notation:

${\begin{aligned}R_{n}f(x;a):=&R_{n}F(1;0)=\int \limits _{0}^{1}{\frac {(1-t)^{n}}{n!}}F^{(n+1)}(t)\,\mathrm {d} t\\=&(n+1)\int \limits _{0}^{1}\sum _{|\alpha |=n+1}{\frac {(1-t)^{n}(x-a)^{\alpha }}{\alpha !}}D^{\alpha }f(a+th)\,\mathrm {d} t\end{aligned}}$

Mehrdimensionale Taylor-Formel

Aus der eindimensionalen Taylor-Formel folgt, dass

$F(1)=T_{n}F(1;0)+R_{n}F(1;0)$

Nach der obigen Definition von $F(t)$ erhält man daher:

$f(x)=T_{n}f(x;a)+R_{n}f(x;a)$

Mehrdimensionale Restgliedformeln

Man kann auch die eindimensionalen Nicht-Integral-Restgliedformeln mithilfe der Formel für $F^{(n)}(t)$ für den mehrdimensionalen Fall verallgemeinern.

Das Schlömilch-Restglied wird so zu

$R_{n}f(x;a)={\frac {(n+1)(1-\theta )^{n+1-p}}{p}}\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}$,

das Lagrange-Restglied zu

$R_{n}f(x;a)=\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}$,

und das Cauchy-Restglied zu

$R_{n}f(x;a)=(n+1)(1-\theta )^{n}\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}$

für jeweils ein $\theta \in [0,1]$.

Qualitative Taylorformel

Nach der mehrdimensionalen Taylorformel ergibt sich mit dem Lagrange-Restglied:

$f(x)-T_{n+1}f(x;a)=(n+1)\left(\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}-\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a)}{\alpha !}}\right)$

Wegen $|x_{i}-a_{i}|\leq \|x-a\|$ erhalten wir ferner:

${\begin{aligned}&(n+1)\left|\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a+\theta h)}{\alpha !}}-\sum _{|\alpha |=n+1}{\frac {(x-a)^{\alpha }D^{\alpha }f(a)}{\alpha !}}\right|\\\leq &(n+1)\|x-a\|^{n+1}\cdot \underbrace {\left|\sum _{|\alpha |=n+1}{\frac {D^{\alpha }f(a+\theta h)-D^{\alpha }f(a)}{\alpha !}}\right|} _{\to 0{\text{, }}x\to a}\end{aligned}}$

Der letzte Teil geht gegen null, da die partiellen Ableitungen vom Grad $n+1$ nach Voraussetzung alle stetig sind und $a+\theta h$ sich zwischen $x$ und $a$ befindet und somit auch nach $a$ konvergiert, falls $x\to a$.

Wir erhalten folgende Abschätzung, welche „(mehrdimensionale) qualitative Taylorformel“ genannt wird:

$f(x)=T_{n+1}f(x;a)+{\mathcal {O}}(\|x-a\|^{n+1})$

für $x\to a$, wobei ${\mathcal {O}}$ für die Landau-Notation steht.

Beispiel

Es soll die Funktion

$f:\{(x_{1},x_{2})\in \mathbb {R} ^{2},\ x_{2}<1\}\to \mathbb {R} ,~(x_{1},x_{2})\mapsto \exp(x_{1}-x_{2})\cdot \log(1-x_{2})$

um den Punkt $a=(a_{1},a_{2})=(1,0)\in \mathbb {R} ^{2}$ entwickelt werden.

Funktion (rot) und Taylorentwicklung (grün)

In diesem Beispiel soll die Funktion bis zum zweiten Grad entwickelt werden, d. h. man will ein Taylorpolynom zweiter Ordnung berechnen, also die sog. Schmiegquadrik. Es gilt also $n=2$. Wegen $|\alpha |\leq n$ müssen, gemäß der Multiindexschreibweise, die Tupel $(0,0)$, $(1,0)$, $(0,1)$, $(2,0)$, $(1,1)$ und $(0,2)$ berücksichtigt werden. Dabei gilt wegen des Satzes von Schwarz, dass

${\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)={\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)$.

Die partiellen Ableitungen der Funktion lauten:

${\frac {\partial f}{\partial x_{1}}}(a)=\left[\exp(x_{1}-x_{2})\cdot \log(1-x_{2})\right]_{x=(1,0)}=0$

${\frac {\partial f}{\partial x_{2}}}(a)=\left[-\exp(x_{1}-x_{2})\cdot \left(\log(1-x_{2})+{\frac {1}{1-x_{2}}}\right)\right]_{x=(1,0)}=-e$

${\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)=\left[\exp(x_{1}-x_{2})\cdot \log(1-x_{2})\right]_{x=(1,0)}=0$

${\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)={\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)=\left[-\exp(x_{1}-x_{2})\cdot \left(\log(1-x_{2})+{\frac {1}{1-x_{2}}}\right)\right]_{x=(1,0)}=-e$

${\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)=\left[\exp(x_{1}-x_{2})\left(\log(1-x_{2})+{\frac {2}{1-x_{2}}}-{\frac {1}{(1-x_{2})^{2}}}\right)\right]_{x=(1,0)}=e$

Es folgt mit der mehrdimensionalen Taylor-Formel:

${\begin{aligned}f(x)\approx &f(a)+{\frac {1}{1!}}{\frac {\partial f}{\partial x_{1}}}(a)~(x_{1}-a_{1})+{\frac {1}{1!}}{\frac {\partial f}{\partial x_{2}}}(a)~(x_{2}-a_{2})\\&+{\frac {1}{2!}}{\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)~(x_{1}-a_{1})^{2}+{\frac {1}{1!1!}}{\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)~(x_{1}-a_{1})(x_{2}-a_{2})\\&+{\frac {1}{2!}}{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)~(x_{2}-a_{2})^{2}\\&=0+0-e(x_{2}-0)+0-e(x_{1}-1)(x_{2}-0)+{\frac {1}{2}}e(x_{2}-0)^{2}\\&=-x_{1}x_{2}e+{\frac {1}{2}}x_{2}^{2}e\end{aligned}}$

Benutzt man die alternative Darstellung mit Hilfe des Gradienten und der Hesse-Matrix, so erhält man:

${\begin{aligned}f(x)&\approx f(a)+\nabla f(a)^{T}(x-a)+{\frac {1}{2}}(x-a)^{T}H_{f}(a)(x-a)\\&=f(a)+{\begin{pmatrix}{\frac {\partial f}{\partial x_{1}}}(a)&{\frac {\partial f}{\partial x_{2}}}(a)\end{pmatrix}}{\begin{pmatrix}x_{1}-a_{1}\\x_{2}-a_{2}\end{pmatrix}}\\&\qquad +{\frac {1}{2}}{\begin{pmatrix}x_{1}-a_{1}&x_{2}-a_{2}\end{pmatrix}}{\begin{pmatrix}{\frac {\partial ^{2}f}{\partial x_{1}^{2}}}(a)&{\frac {\partial ^{2}f}{\partial x_{2}\partial x_{1}}}(a)\\{\frac {\partial ^{2}f}{\partial x_{1}\partial x_{2}}}(a)&{\frac {\partial ^{2}f}{\partial x_{2}^{2}}}(a)\end{pmatrix}}{\begin{pmatrix}x_{1}-a_{1}\\x_{2}-a_{2}\end{pmatrix}}\\&=0+{\begin{pmatrix}0&-e\end{pmatrix}}{\begin{pmatrix}x_{1}-1\\x_{2}\end{pmatrix}}+{\frac {1}{2}}{\begin{pmatrix}x_{1}-1&x_{2}\end{pmatrix}}{\begin{pmatrix}0&-e\\-e&e\end{pmatrix}}{\begin{pmatrix}x_{1}-1\\x_{2}\end{pmatrix}}\\&=-x_{1}x_{2}e+{\frac {1}{2}}x_{2}^{2}e\end{aligned}}$

Literatur

• Otto Forster: Analysis. Band 1: Differential- und Integralrechnung einer Veränderlichen. 8. verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2006, ISBN 3-8348-0088-0 (Vieweg Studium. Grundkurs Mathematik).
• Otto Forster: Analysis. Band 2: Differentialrechnung im Rⁿ. Gewöhnliche Differentialgleichungen. 7. verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2006, ISBN 3-8348-0250-6 (Vieweg Studium. Grundkurs Mathematik).
• Konrad Königsberger: Analysis. Band 2. 3. überarbeitete Auflage. Springer-Verlag, Berlin u. a. 2000, ISBN 3-540-66902-7.
• Bernhard Heck: Rechenverfahren und Auswertemodelle der Landesvermessung, Kapitel 4, 7 und 13 (Mathematische Modelle und Grundlagen). Wichmann-Verlag, Karlsruhe 1987.