Begriffsschrift

Die Begriffsschrift ist ein schmales, nur etwa achtzig Seiten umfassendes Buch des Jenaer Mathematikers und Philosophen Gottlob Frege zur Logik. Es wurde 1879 mit dem Untertitel „Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens“ veröffentlicht und gilt allgemein als die wichtigste Veröffentlichung im Bereich der Logik seit Aristoteles’ Organon.[1]
Frege gelang in diesem Buch zum ersten Mal eine Formalisierung der klassischen Prädikatenlogik und damit die erste Formalisierung einer Logik, in der sich ein hinreichend großer Teil der Mathematik, aber auch der natürlichen Sprache ausdrücken ließ. Gemeinsam mit George Booles Mathematical Analysis of Logic von 1847 markiert die Begriffsschrift deshalb den Beginn der modernen formalen Logik.[2] Die Bezeichnung Begriffsschrift wird auch für den von Frege definierten logischen Kalkül sowie für Freges logische Notation verwendet. Frege entwarf die Begriffsschrift zur Unterstützung seiner Forschung an den Grundlagen der Mathematik.
Freges Kalkül führte erstmals den Allquantor sowie mehrstellige Prädikate (Relationen) ein. Es handelt sich um einen klassischen prädikatenlogischen Kalkül zweiter Stufe mit Identität, allerdings in einer im Vergleich zu heute üblichen Schreibweisen eigenwilligen, zweidimensionalen Notation.
Stellung der Begriffsschrift im Gesamtwerk Freges
[Bearbeiten | Quelltext bearbeiten]Trotz ihrer epochalen Bedeutung ist die Begriffsschrift nicht Freges Hauptwerk. Ihr folgten 1884 Die Grundlagen der Arithmetik sowie 1893 und 1903 die beiden Bände der Grundgesetze der Arithmetik, die auch aufgrund ihres Umfangs als Freges Hauptwerk gelten können.

Freges Motivation: Freges vorrangiges Ziel war es, die Mathematik als Teil der Logik auszuweisen, also zu zeigen, dass alle mathematischen Sätze aus wenigen rein logischen Axiomen abgeleitet werden können (vgl. Logizismus). Dieses Unternehmen wäre nur aussichtsreich, wenn eine ‹Formelsprache des reinen Denkens› zur Verfügung steht, mit dem sich die ‹Lückenlosigkeit einer Schlusskette› zweifelsfrei überprüfen ließe, und das (wie Frege sagt) nur mit dem ‹begrifflichen Inhalt› des jeweiligen Satzes, ‹ohne Anschauliches›, was ‹von der besonderen Beschaffenheit der Dinge unabhängig› bestehe.[3] Dieses Instrument, ein ‹zweckdienliches Werkzeug zur Untersuchung beliebiger sprachlicher Ausdrucksformen›,[4] soll die Begriffsschrift darstellen. Die so verstandene Zweckmäßigkeit, zu dem Ziel einer umfassenden Reduktion der Arithmetik auf die Formen von ‹Denkgesetzen›, erzwingt, so Freges bleibende Grundüberzeugung, das ‹Gebot der Übersichtlichkeit›, und dazu gehört die Minimierung logischer Schlussweisen und Operatoren bei größtmöglicher Ausdrucksstärke, um so dem rein ‹begrifflichen Inhalt› den nötigen Platz zu geben.[5][6] In seiner nachträglichen Rechtfertigung hebt Frege genau diesen Punkt als entscheidende Neuerung, auch gegenüber traditionellen Logiksystemen, hervor.
„Jeder Versuch, hier an die Stelle der einfachen Buchstaben Ausdrücke von Inhalten, etwa analytische Gleichungen zu setzen, würde durch die Unübersichtlichkeit, Schwerfälligkeit, ja Vieldeutigkeit der entstehenden Formeln zeigen, wie wenig geeignet diese Bezeichnungsweise zur Bildung einer wahren Begriffsschrift ist. Von einer solchen möchte ich Folgendes verlangen. Sie muß für die logischen Beziehungen einfache Ausdrucksweisen haben, die, an Zahl auf das Nothwendige beschränkt, leicht und sicher zu beherrschen sind. Diese Formen müssen geeignet seyn, sich mit dem Inhalte auf das Innigste zu verbinden. […] Wenn die allgemeinen Formen einmal vorhanden sind, können [die Zeichen von inhaltlicher Bedeutung] leicht nach Bedürfnis geschaffen werden.“
Für Frege war die Begriffsschrift demnach nur die erste Etappe auf dem Weg zu einer vollständigen Formalisierung der Mathematik, die er in den Grundgesetzen der Arithmetik für die Zahlentheorie teilweise durchführte. Freges logizistisches Programm scheiterte zunächst (noch vor dem Erscheinen des zweiten Bandes der Grundgesetze) an der Russellschen Antinomie, es wurde aber von Bertrand Russell, Rudolf Carnap und anderen fortgeführt.
Die Begriffsschrift war jedoch keineswegs ausschließlich für den Einsatz in der Mathematik vorgesehen. Im Gegenteil stellte Frege seine Schrift im Vorwort ausdrücklich in den Kontext der Leibnizschen Idee einer lingua characterica universalis, einer Universalsprache, die ein geordnetes System aller Begriffe nach mathematischem Vorbild darstellen sollte.[8][9][10][11][12] Freges 1879 vorgelegte Schrift sollte das logische Herzstück einer solchen Universalsprache bilden.
Es ist zu vermuten, dass die Bezeichnung Begriffsschrift aus einer Abhandlung Friedrich Adolf Trendelenburgs[13] über Leibniz’ Entwurf dieser Universalsprache entlehnt ist, die Frege im Vorwort zitiert.[14] Im Übrigen war das Wort „Begriffsschrift“ um die Wende zum 20. Jahrhundert als Eindeutschung von „Ideographie“ allgemein gebräuchlich.[15]
Notation
[Bearbeiten | Quelltext bearbeiten]
Zum Öffnen bitte auf die Vorschau klicken.
Frege verwendete in der Begriffsschrift eine eigens von ihm geschaffene Schreibweise (Notation) für Ausdrücke der Aussagen- und Prädikatenlogik. Die Notation der Begriffsschrift ist eine graphische, zweidimensionale Darstellung, in der Formeln durch waagerechte und senkrechte Striche miteinander verbunden werden. Sie verwendet als aussagenlogische Grundelemente Zeichen für die Negation und das Konditional, als prädikatenlogisches Element den Allquantor. Wie erst sehr viel später die – allerdings lineare, eindimensionale und daher wesentlich platzsparendere – polnische Notation kommt die Begriffsschriftnotation ohne Klammerungen aus.
Syntax
[Bearbeiten | Quelltext bearbeiten]Die Begriffsschrift kennt nur zwei syntaktische Grundelemente: Funktionsausdrücke und Eigennamen, wobei beide auch durch Variablen vertreten werden können. Alle syntaktischen Operationen folgen dem Schema Funktion – Argument – Wert: Durch Anwendung einer Funktion mit n freien Stellen auf n Argumente erhält man einen bestimmten Wert der Funktion.
Näheres zum Funktionsbegriff: Wenn man beispielsweise in dem komplexen Ausdruck '1 × 1' beide Vorkommnisse des Zahlzeichens '1' durch die Variablen 'n' bzw. 'm' ersetzt, so erhält man den Funktionsausdruck 'n × m'. Die Variablen machen deutlich, dass der Ausdruck „ungesättigt“ ist, wie Frege sagt: Er bezeichnet in dieser Form keinen Gegenstand, sondern bedarf der Vervollständigung durch zwei Argumente. Durch erneute Substitution von Zahlzeichen für die Variablen erhält man eine Reihe von arithmetischen Termen, z. B. '1 × 1', '1 × 2', '2 × 1' usw. Die verschiedenen möglichen Einsetzungen für die Variablen sind Argumentausdrücke. Das durch den komplexen Ausdruck Bezeichnete ist der Wert der Funktion. Der Wert der Funktion n × m für die Argumente 2 und 3 ist beispielsweise die Zahl 6.
Dieses Grundschema ist in seiner Anwendbarkeit keineswegs auf den Bereich der Mathematik beschränkt: Ersetzt man beispielsweise in 'der Eroberer von x' die Variable 'x' durch 'Gallien', so nimmt die Funktion den Wert Julius Cäsar an.[16] Auch Prädikate sind nach Frege Funktionen: Die durch 'x eroberte Gallien' ausgedrückte Funktion nimmt für das Argument Julius Cäsar den Wert Wahr an, für das Argument Hannibal den Wert Falsch. Die Ersetzung der Subjekt-Prädikat-Form durch die Funktion-Argument-Form des Urteils war bereits ein erheblicher Fortschritt gegenüber der traditionellen Logik, weil sie es ermöglicht, eine Logik der Relationen zu formulieren: Die moderne Logik kennt (anders als die Syllogistik) auch zwei- und mehrstellige Prädikate (Relationsausdrücke), wie 'x liebt y', 'x steht zwischen y und z' usw. (Siehe auch Logik – Klassische Logik.)
Wahrheitsfunktionalität
[Bearbeiten | Quelltext bearbeiten]Frege fasste nun alle zusammengesetzten Ausdrücke als Ergebnisse der Anwendung einer Funktion auf Argumente auf; insbesondere behandelte er auch diejenigen Ausdrücke als Funktionsausdrücke, die heute allgemein als Junktoren bekannt sind. Ihre Argumente sind Aussagen, als Werte ergeben sich die Wahrheitswerte Wahr und Falsch, die bei Frege „das Wahre“ und „das Falsche“ heißen. Um die Bedeutung eines Junktors anzugeben, genügt es, festzulegen, unter welchen Bedingungen eine Aussage mit diesem Junktor wahr bzw. falsch wird. Heute wird dieser Zusammenhang als Wahrheitsfunktionalität bezeichnet, und man gibt die Wahrheitsbedingungen meist in Form sogenannter Wahrheitstabellen an. Die Wahrheitsfunktionalität ist eine wesentliche Voraussetzung für die Aufstellung einer extensionalen Semantik, wie sie Alfred Tarski in den 1930er Jahren entwickelte.
Inhaltsstrich und Urteilsstrich
[Bearbeiten | Quelltext bearbeiten]Der waagerechte „Inhaltsstrich“ besagt in der Begriffsschrift, dass das, was auf ihn folgt, ein (auf Wahrheit oder Falschheit hin) „beurtheilbarer Inhalt“[17] ist, in moderner Terminologie eine Aussage, die wahr oder falsch sein kann. Durch den Inhaltsstrich wird nicht über den Wahrheitsgehalt einer Aussage befunden; sie wird nicht behauptet, sondern nur als potenziell wahr oder falsch gleichsam „in den Raum gestellt“:
Wohlgemerkt wäre eine absurd erscheinende Verbindung wie „— 2“ in der Begriffsschrift nicht syntaxwidrig; ihr Wert wäre das Falsche. Das hängt damit zusammen, dass Freges Begriffsschrift eine reine Termlogik ist; auch Aussagen sind singuläre Terme, gewissermaßen verschiedene Bezeichnungen für die beiden Wahrheitswerte.
Der senkrechte „Urteilsstrich“ vor dem Inhaltsstrich besagt, dass der Inhalt wahr ist:
Frege sagte dazu, der Inhalt werde mit „behauptender Kraft“ geäußert.
Junktoren
[Bearbeiten | Quelltext bearbeiten]
Frege verwendete von den heute üblichen fünf Junktoren 'nicht', 'und', 'oder', 'wenn – dann', 'genau dann, wenn' nur zwei: 'nicht' (Negation) und 'wenn – dann' (Implikation oder Konditional). Die Negation wird durch Anfügen eines kleinen senkrechten Striches an den Inhaltsstrich dargestellt. Die Negation „nicht A“ () wird folgendermaßen ausgedrückt:
Der Wert dieser Funktion ist genau dann das Wahre, wenn der Wahrheitswert von '— A' nicht das Wahre ist, andernfalls das Falsche.
Die Implikation (lies: 'wenn B, dann A') wird in der Begriffsschrift durch
ausgedrückt. Zur Bedeutung dieser Zeichenverbindung schrieb Frege:
„Wenn A und B beurtheilbare Inhalte bedeuten, so giebt es folgende vier Möglichkeiten:
- A wird bejaht und B wird bejaht;
- A wird bejaht und B wird verneint;
- A wird verneint und B wird bejaht;
- A wird verneint und B wird verneint.
bedeutet nun das Urtheil, dass die dritte dieser Möglichkeiten nicht stattfinde, sondern eine der drei andern.“[17]
Dies sind in heute ungewohnt erscheinender Formulierung die Wahrheitsbedingungen der materialen Implikation: Die Implikation ist nur dann falsch, wenn das Antezedens wahr und das Sukzedens falsch ist.
Disjunktion ('oder') und Konjunktion ('und') lassen sich durch Verbindungen dieser beiden Junktoren ausdrücken: die Disjunktion wird durch
– – ausgedrückt, die Konjunktion durch
– . Da Freges Logik eine Termlogik ist, in der auch Aussagen singuläre Terme sind, dient das „Zeichen der Inhaltsgleichheit“ (Identitätszeichen) zugleich als Ausdruck der materialen Äquivalenz.
Quantoren
[Bearbeiten | Quelltext bearbeiten]
Als Allquantor verwendet Frege eine Einbuchtung („Höhlung“) im Inhaltsstrich, in die die zu bindende Variable geschrieben wird (siehe nebenstehende Grafik). Aufgrund der in der klassischen Prädikatenlogik geltenden Äquivalenz
ist ein eigener Existenzquantor nicht erforderlich; sein Inhalt kann durch Allquantor und Negator ausgedrückt werden.
Das folgende Beispiel zeigt die Aussage „zu jedem x mit der Eigenschaft F gibt es ein y, zu dem x in der Beziehung R steht“ (z. B. „jeder Mensch hat eine Mutter“). Es illustriert die beiden wesentlichen Errungenschaften der Begriffsschrift, die sie sowohl gegen die traditionelle Syllogistik als auch gegen die zeitgenössische logische Algebra abgrenzt: verschachtelte Quantoren („für alle x gibt es ein y“) und mehrstellige Prädikate („R(x,y)“).
Aus dieser Aussage folgt mit Axiom 9 (siehe unten):
Daraus kann in Verbindung mit der Aussage „F(c)“ mit Hilfe der Regel Modus ponens (Das Axiomensystem – siehe unten) die Aussage „es gibt ein y, zu dem c in R steht“ abgeleitet werden:
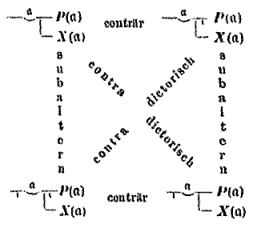
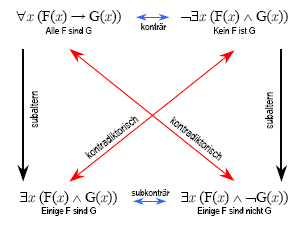
Die Quantorenlogik erlaubt (unter der Voraussetzung, dass der Subjektterm nicht leer ist) sämtliche Schlüsse der traditionellen Logik. Die nachstehende Abbildung zeigt links das „logische Quadrat“ aus der Originalausgabe der Begriffsschrift,[18] rechts eines in moderner Schreibweise zum Vergleich:
Dass bei Frege in der unteren Zeile „conträr“ statt „subconträr“ steht, ist offenbar ein Versehen.[19]
Siehe auch die tabellarische Übersicht zur Notation am Ende des Artikels.
Das Axiomensystem der Begriffsschrift
[Bearbeiten | Quelltext bearbeiten]Nach den Erläuterungen zur Schreibweise im ersten Kapitel geht Frege im zweiten Kapitel mit der Überschrift „Darstellung und Ableitung einiger Urtheile des reinen Denkens“ dazu über, einige logisch wahre Sätze auf der Grundlage weniger Axiome zu beweisen.
Frege rechtfertigte seine neun Axiome nicht-formal, indem er begründete, warum sie in ihrer intendierten Interpretation wahr sind. In moderne Schreibweise übersetzt, lauten die Axiome:[20]
Dies sind in Freges eigener Nummerierung die Sätze 1, 2, 8, 28, 31, 41, 52, 54 und 58.[21] (1)–(3) betreffen die materiale Implikation, (4)–(6) die Negation. (7) und (8) betreffen die Identität: (7) ist das Identitätsprinzip von Leibniz.[22] (8) fordert die Reflexivität der Identität. (9) erlaubt den Übergang von einer allquantifizierten Aussage zu einer beliebigen Instanz. Alle übrigen Sätze werden aus diesen Axiomen abgeleitet.
Die Begriffsschrift hat drei Folgerungsregeln. Zwei davon, der Modus ponens und die Generalisierungsregel, werden explizit genannt. Der Modus ponens erlaubt den Übergang von und zu . Die Generalisierungsregel erlaubt den Übergang von zu , wenn die Variable 'x' nicht in P vorkommt.[23] Die dritte, nicht explizit genannte Regel ist ein Substitutionsprinzip.
Das einer Prädikatenlogik der ersten Stufe entsprechende Fragment des in der Begriffsschrift angegebenen Kalküls ist vollständig und widerspruchsfrei.[24][25][26] Erst die Erweiterung des Systems um eine Theorie der Begriffsumfänge, die Frege später in den Grundgesetzen der Arithmetik vornahm, führte zur Inkonsistenz.[27]
Das dritte Kapitel trägt die Überschrift „Einiges aus einer allgemeinen Reihenlehre“. Die wichtigsten Ergebnisse[28] betreffen die Erblichkeit einer Eigenschaft in einer Reihe und das Nachfolgen in einer Reihe. Ist eine Relation R gegeben, so ist eine Eigenschaft F nach Frege erblich in der R-Reihe genau dann, wenn gilt:
Anschließend definiert Frege: b folgt in der R-Reihe auf a genau dann, wenn b jede in der R-Reihe erbliche Eigenschaft hat, die alle x mit aRx haben. Schreibt man R* für diese Relation des Folgens in der R-Reihe, so lässt sich Freges Definition wie folgt wiedergeben:
Kürzer, wobei „Erbl(F,R)“ bedeuten soll „F ist erblich in der R-Reihe“:
Über diese R*-Relation beweist Frege in der Folge einige Sätze, die zeigen, dass es sich um eine Ordnungsrelation handelt. Diese Betrachtungen sind ganz offensichtlich als Vorarbeiten zu den beiden Nachfolgewerken zu den Grundlagen der Zahlentheorie intendiert. Wenn man als xRy die Relation y=x+1 betrachtet, dann ist 0R*y (oder 1R*y) die Eigenschaft von y, eine natürliche Zahl zu sein.
Rezeption und Wirkung
[Bearbeiten | Quelltext bearbeiten]Beurteilung des logischen Fortschritts durch die Begriffsschrift
[Bearbeiten | Quelltext bearbeiten]Die Begriffsschrift fand zunächst eine bemerkenswert kühle Aufnahme. Nicht zuletzt aufgrund ihrer ungewohnten und schwer lesbaren Symbolik scheint die breite Fachöffentlichkeit zunächst wenig Notiz von ihr genommen zu haben. Der Tenor der zeitgenössischen Rezensionen war größtenteils verhalten bis kritisch.[14][30] Einhellig wurden Bedenken gegenüber der raumgreifenden, schwer handhabbaren Schreibweise geäußert. Vor allem aber warfen die Kritiker Frege vor, den algebraischen Ansatz in der symbolischen Logik (Ernst Schröder, Giuseppe Peano, George Boole, Augustus De Morgan, Charles Sanders Peirce) zu ignorieren. Die Kritik ist berechtigt: Es ist auffällig, dass Frege die seinerzeit dominante Strömung der formalen Logik völlig übergeht und seine eigene Arbeit nicht zu der anderer zeitgenössischer Forscher in Beziehung setzt. Dieses Versäumnis holte er in einigen unmittelbar auf die Begriffsschrift folgenden Aufsätzen nach.[31]
Zu den wenigen, die schon früh die Bedeutung der Begriffsschrift erkannten, zählte der britische Philosoph und Mathematiker Bertrand Russell. Das wird bereits daran deutlich, dass Russell in seinem ersten umfassenden Logikband, den Principles of Mathematics (1903), dem logischen System Freges nach der Begriffsschrift und den Grundgesetzen der Arithmetik einen eigenen Anhang widmete. Bemerkenswert ist darin gleich der erste Satz: „Das Werk von Frege, das weit weniger bekannt zu sein scheint als es verdient, enthält viele der Lehrsätze, die in […] der gegenwärtigen Arbeit fortgesetzt wurden“.[32] Insbesondere bestätigte Russell die von Frege selbst behauptete Unabhängigkeit und Übergeordnetheit des Kalküls der Begriffsschrift gegenüber traditionellen Systemen und erkannte damit als einer der ersten den wegweisenden Fortschritt für die Mathematische Logik.[33]
Das logizistische Programm, zu dem die Begriffsschrift nur der Auftakt war, wurde insbesondere durch Russell und Alfred North Whitehead in ihren monumentalen Principia Mathematica (1910 ff.) fortgeführt, die geraume Zeit als das kanonische Standardwerk zur Logik galten. Russell und Whitehead verwendeten bereits im Wesentlichen eine der heute üblichen logischen Notationen, die an die Schreibweise der Algebra angelehnte sogenannte Peano-Russell-Notation.
In dieselbe Richtung zielend, aber mit mehr Distanz als Russell und in Abgrenzung zum Peanoschen Logiksystem, wusste Kurt Gödel die besondere Leistung des Fregeschen Werkes zu beurteilen, der die von Frege behauptete ‹Zweckmäßigkeit›[34] der Begriffsschrift in seiner logizistischen Zielsetzung sieht, hingegen in Sachen Flexibilität des Formalismus Defizite feststellt: „Frege war hauptsächlich an der Analyse des Gedankens interessiert und gebrauchte seinen Kalkül an erster Stelle, um die Arithmetik aus der reinen Logik abzuleiten. Peano andererseits war mehr an seinen Anwendungen innerhalb der Mathematik interessiert und schuf einen eleganten und flexiblen Symbolismus […].“[35][36]
Auch sind die Einflüsse Freges auf die Phänomenologe Edmund Husserl und auf dessen eigene Logische Untersuchungen zu erwähnen, ebenso wie der auf Freges Schüler Rudolf Carnap, der die Idee einer formallogischen Wissenschaftssprache hinter Freges System mit aller Konsequenz fortsetzte. Nicht zuletzt ist der österreichisch-britische Philosoph Ludwig Wittgenstein zu nennen, der im Vorwort zu seinem berühmten Tractatus logico-philosophicus (1921) schrieb: „Nur das will ich erwähnen, daß ich den großartigen Werken Freges und den Arbeiten meines Freundes Herrn Bertrand Russell einen großen Teil der Anregung zu meinen Gedanken schulde.“[37]
Alfred Tarski würdigt in seiner wegweisenden Logikschrift Introduction to Logic (1936/1941) Freges Aussagenkalkül der Begriffsschrift in besonderem Maße: „Das historisch erste System des Aussagenkalküls ist in dem Werke Begriffsschrift [… des] Logikers G. Frege (1848 – 1925) enthalten, der ohne Zweifel der größte Logiker des 19. Jh.s gewesen ist“.[38] Außerdem betont Tarski das damit verbundene logizistische Bemühen Freges als schöpferischen Beitrag für die gesamte moderne Logik: „[D]ie bloße Tatsache, daß es gelungen ist, die ganze Arithmetik samt allen auf ihr aufgebauten Disziplinen […] als einen Teil der Logik zu entwickeln, stellt eine der schönsten Errungenschaften der neueren logischen Forschung dar. Die grundlegenden Gedanken in diesem Gebiete stammen von Frege.“[39]
Freges Axiomensysteme der Aussagenlogik und der Prädikatenlogik erster Stufe werden in neueren Lehrbüchern der mathematischen Logik nahezu unverändert verwendet, um daran die zentralen logischen Metatheoreme zu behandeln.[40]
Abgrenzung von der Aristotelischen Syllogistik
[Bearbeiten | Quelltext bearbeiten]Als entscheidender Fortschritt innerhalb der formalen Logik gilt heute dasjenige, was Frege selbst in seiner Begriffsschrift schon hervorhebt. Von Beginn an wird die Subjekt-Prädikat-Form der traditionellen Syllogistik durch die Funktions-Argument-Struktur ersetzt, in der wiederum sowohl für Funktionen als auch für Argumente Variablen oder Konstanten auftreten können. Zudem wird die Funktion in davon unabhängigen, mehrstelligen Relations-Aussagen zugelassen.[41] In dieser Hinsicht können die traditionellen Systeme nicht zu einem Relationskalkül erweitert werden, eine syntaktische Einschränkung, die Frege für sein Programm nicht hinnehmen konnte:
„Gerade die Beziehungen spielen aber nun in dem logischen Aufbau der Mathematik die wesentliche Rolle. Der Irrtum, daß die traditionelle Logik ausreiche, um die Mathematik aus ihren Grundlagen heraus logisch aufzubauen, konnte nur dadurch zustande kommen, das vor Frege und Peano niemand eine restlose Analyse der in der Mathematik verwendeten logischen Schlußweisen vorgenommen hat. In den älteren Logikbüchern [...] wird nie der Beweis irgendeines wichtigen mathematischen Satzes in alle Einzelheiten zerlegt.“
Frege illustriert die Erweiterung in seinem System durch den Nachweis, wie gewisse Formen der Aristotelischen Syllogistik darin enthalten sind.[43][44][45][46]
Zu bemerken ist auch die Eingrenzung, dass in Freges Begriffsschrift der traditionelle Unterschied zwischen faktischer und notwendiger Allgemeinheit, der modallogische Aspekt der traditionellen Schlussformen aufgehoben wurde, zugunsten der Beschränkung auf assertorische Urteilsformen (im Sinne Kants).[47][48] Frege, sich dieser Eingrenzung durchaus bewusst, verstand modale Aussagen nicht als dem ‹begrifflichen Inhalt des Urteils› zugehörig.[49]
Freges Symbolik in der heutigen Formalen Logik
[Bearbeiten | Quelltext bearbeiten]Aus Freges Symbolik überlebte (wohl durch Vermittlung der Principia Mathematica) das Zeichen , die Kombination aus seinem Urteils- und Inhaltsstrich, allerdings meist in einer verallgemeinerten Bedeutung als Ableitungsrelation.[50] Ferner kann das heute übliche Negationszeichen , das Arend Heyting 1930[51] einführte (ursprünglich zur Unterscheidung des intuitionistischen Negators vom klassischen), als Inhaltsstrich mit angefügtem Verneinungsstrich betrachtet werden.
Auch wenn Freges eigenwilliger Schreibweise kein großer Erfolg beschieden war, fußt nahezu jede Arbeit in der modernen Logik wenigstens mittelbar auf den Grundgedanken der Begriffsschrift. Da die Logik ferner Hilfs- und Grundlagendisziplin u. a. der Mathematik, Linguistik und Informatik ist, sind die indirekten Auswirkungen von Freges Werk kaum zu überschauen. In der Philosophie beziehen sich bis in die allerjüngste Vergangenheit immer wieder anerkannte Persönlichkeiten auf Ideen aus der Begriffsschrift, darunter beispielsweise Michael Dummett und Robert Brandom.
Tabellarische Übersicht der Schreibweise
[Bearbeiten | Quelltext bearbeiten]Ausgaben
[Bearbeiten | Quelltext bearbeiten]- Begriffsschrift. Eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle 1879. Originalausgabe: hier auch mit Frege: Begriffsschrift (1879) abgekürzt.
- Begriffsschrift und andere Aufsätze, herausgegeben von Ignacio Angelelli, Hildesheim 1964 u.ö., ISBN 978-3-487-00623-9
[Diese Reprintausgabe hat einige kleine, aber zum Teil sinnstörende Druckfehler; insbesondere fehlt gleich auf S. 1 der Urteilsstrich. Siehe dazu die Notiz von Angelelli/Bynum in der Literaturliste.]
Literatur
[Bearbeiten | Quelltext bearbeiten]- Ignacio Angelelli, Terrell Ward Bynum: Note on Frege’s Begriffsschrift. In: Notre Dame Journal of Formal Logic. Band 7, Nr. 4, 1966, ISSN 0029-4527, S. 369–370, doi:10.1305/ndjfl/1093958759 (projecteuclid.org – Im Wesentlichen eine Korrigendaliste zur Reprintausgabe der Begriffsschrift von Angelelli.).
- Franz Bolck (Hrsg.): Begriffsschrift. Jenaer Frege-Konferenz: 7.–11. Mai 1979. Jena 1979.
- George Boolos: Reading the Begriffsschrift. In: Mind. XCIV, Nr. 375, 1985, ISSN 0026-4423, S. 331–344, doi:10.1093/mind/XCIV.375.331. Wiederabdruck in: ders.: Logic, Logic, and Logic, Cambridge (Mass.) 1998, 202–219, ISBN 978-0-674-53767-5.
- John P. Burgess: On a Consistent Subsystem of Frege's Grundgesetze. In: Notre Dame Journal of Formal Logic. Band 39, Nr. 2, 1998, S. 274–278, doi:10.1305/ndjfl/1039293068.
- Gottlob Frege: Anwendungen der Begriffsschrift. Vortrag, gehalten in der Sitzung vom 24. Januar 1879 der Jenaischen Gesellschaft für Medizin und Naturwissenschaft. In: Jenaische Zeitschrift für Naturwissenschaft 13/Supplement II. (1879) (Sitzungsberichte der Jenaischen Gesellschaft für Medizin und Naturwissenschaft für das Jahr 1879), 29–33. (Enthalten in der Reprintausgabe von I. Angelelli.)
- Gottlob Frege: Über die wissenschaftliche Berechtigung einer Begriffsschrift. In: Zeitschrift für Philosophie und philosophische Kritik. Band 81, 1882, S. 48–56. (Enthalten in der Reprintausgabe von I. Angelelli.) Online: Textarchiv – Internet Archive (Zugriff: 3. Juli 2024).
- Gottlob Frege: Über den Zweck der Begriffsschrift. In: Jenaische Zeitschrift für Naturwissenschaft. 16 (1883) Supplement, 1–10. (Enthalten in der Reprintausgabe von I. Angelelli.)
- Gottlob Frege: Booles logische Formelsprache und meine Begriffsschrift. In: ders.: Nachgelassene Schriften. 53–59.
- Gottlob Frege: Booles rechnende Logik und die Begriffsschrift. In: ders.: Nachgelassene Schriften. 9–52.
- Gottlob Frege: Funktion und Begriff. (Vortrag, gehalten in der Sitzung am 9. Januar 1891 der Jenaischen Gesellschaft für Medizin und Naturwissenschaft. Greifbar in ders.: Funktion, Begriff, Bedeutung.)
- Gottlob Frege: Nachgelassene Schriften. herausgegeben von Hans Hermes, Friedrich Kambartel und Friedrich Kaulbach, Hamburg 1969; erweiterte zweite Auflage 1983, ISBN 978-3-7873-0490-5.
- Gottlob Frege: Funktion, Begriff, Bedeutung. Fünf logische Studien. herausgegeben von G. Patzig, Göttingen 1994 u.ö., ISBN 978-3-525-33377-8.
- J. J. Green, Marcus Rossberg, Philip A. Ebert: The Convenience of the Typesetter. Notation and Typography in Frege’s „Grundgesetze der Arithmetik“. In: The Bulletin of Symbolic Logic. Band 21, Nr. 1, Mai 2015, S. 15–30, JSTOR:43229903 (Beschreibt die begriffsschriftliche Notation der Grundgesetze.).
- Gottfried Gabriel, Traditionelle und moderne Logik. In: W. Stelzner, M. Stöckler (Hrsg.), Zwischen traditioneller und moderner Logik – Nichtklassische Ansätze. (Mentis) Paderborn 2001: Seite 21 – 35.
- Otfried Höffe: Kleine Geschichte der Philosophie. München 2008, ISBN 978-3-406-57385-9.
- Tapio Korte: Frege’s Begriffsschrift as a lingua characteristica. In: Synthese. Band 174, Nr. 2, 2010, S. 283–294, doi:10.1007/s11229-008-9422-7 (springer.com).
- Franz von Kutschera: Gottlob Frege. Eine Einführung in sein Werk, Berlin/New York 1989, ISBN 978-3-11-012129-2.
- Danielle Macbeth: Frege’s Logic. Cambridge (Mass.) 2005, ISBN 978-0-674-01707-8.
- Richard L. Mendelsohn: The Philosophy of Gottlob Frege, Cambridge 2005, ISBN 978-0-521-83669-2.
- Terence Parsons: On the consistency of the first-order portion of Frege's logical system. In: Notre Dame Journal of Formal Logic. Band 28, Nr. 1, 1987, S. 161–168, doi:10.1305/ndjfl/1093636853 (projecteuclid.org).
- Ernst Schröder: Anzeige von Freges Begriffsschrift. In: Zeitschrift für Mathematik und Physik. Band 25, 1881, S. 81–94.
- Hans Sluga: Frege against the Booleans. In: Notre Dame Journal of Formal Logic. Band 28, Nr. 1, 1987, S. 80–98, doi:10.1305/ndjfl/1093636848 (projecteuclid.org).
- John Venn: A Review of Frege’s Begriffsschrift. In: Mind. Band 5, 1880, S. 297.
- Risto Vilkko: The Reception of Frege’s Begriffsschrift. In: Historia Mathematica. Band 25, Nr. 4, November 1998, ISSN 0315-0860, S. 412–422, doi:10.1006/hmat.1998.2213 (Enthält einen Überblick über die zeitgenössische Rezeption.).
- Matthias Wille: Gottlob Frege: Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Berlin, Springer Spektrum, 2018 (Klassische Texte der Wissenschaft), ISBN 978-3-662-45011-6.
- Michael Wolff: Freges Kritik an der kantischen Urteilstafel in seiner 'Begriffsschrift' von 1879. In: Michael Wolff: Die Vollständigkeit der kantischen Urteilstafel. Mit einem Essay über Freges 'Begriffsschrift'. Klostermann, Frankfurt 1995, ISBN 3-465-02811-2, S. 243–312.
- Michael Wolff: Frege und das traditionelle Bild der Syllogistik. In: Rüdiger Bubner und Gunnar Hindrichs (Hrsg.): Von der Logik zur Sprache. Klett-Cotta, Stuttgart 2007, ISBN 978-3-608-94448-8, S. 272–285.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Edward N. Zalta: Frege's Theorem and Foundations for Arithmetic. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Frege: Begriffsschrift (1879) in digitaler Form zum Herunterladen
- Eine Darstellung des logischen Systems der Begriffsschrift von Stanley N. Burris (in englischer Sprache)
- Eine kurze Einführung in Gottlob Freges Begriffsschrift von Sven-Ake Wegner (Bergische Universität Wuppertal)
- Ein interaktives Programm zur Umwandlung aussagenlogischer Ausdrücke in die Begriffsschriftnotation (und in andere Notationen) von Christian Gottschall
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Höffe: Kleine Geschichte der Philosophie. S. 318.
- ↑ Dale Jaquette, Introduction: Philosophy of Logic Today. Seite 3 in D. Jaquette (Hrsg.), Philosophy of Logic (Handbook of the Philosophy of Science). Elsevier 2007. Online-Veröffentlichung: Science Direct (Zugriff 5 Juli 2024).
- ↑ So Frege in seinem Vorwort, S. IV, und in § 3 der Begriffsschrift.
- ↑ Siehe Frege: Begriffsschrift (1879), S. VI/VII sowie §6, S. 9 f.
- ↑ Siehe Frege: Begriffsschrift (1879), Vorwort S. IV; § 6, S. 9 und Frege (1882), S. 54 f.
- ↑ Siehe auch Gabriel (2001), hier in der Literatur: Seite 31.
- ↑ G. Frege, Über die wissenschaftliche Berechtigung einer Begriffsschrift. Seite 54 f. in: Zeitschrift für Philosophie und philosophische Kritik. Band 81, 1882. (Hier auch in der Literatur angegeben.)
- ↑ Vgl. Sluga: „Frege against the Booleans“
- ↑ Vgl. Volker Peckhaus: Logik, Mathesis universalis und allgemeine Wissenschaft, Berlin 1997, ISBN 978-3-05-003111-8
- ↑ Vgl. Tapio Korte: „Frege’s Begriffsschrift as a lingua characteristica“.
- ↑ Eine überaus kritische Skizze der Überlegungen zu einer solchen Universalsprache findet sich im Artikel „Universalsprache“ in: Fritz Mauthner: Wörterbuch der Philosophie, zweite, vermehrte Auflage, Leipzig 1923. (online)
- ↑ Vgl. den Artikel „Charakteristica universalis“ in: Friedrich Kirchner/Carl Michaëlis: Wörterbuch der Philosophischen Grundbegriffe, 5. Aufl. Leipzig 1907, 116–117. (online)
- ↑ Adolf Trendelenburg: „Über Leibnizens Entwurf einer allgemeinen Charakteristik,“ in: Philosophische Abhandlungen der königlichen Akademie der Wissenschaften zu Berlin aus dem Jahre 1856, Berlin 1857, 36–69; Nachdruck in: ders.: Historische Beiträge zur Philosophie, Bd. 3: Vermischte Abhandlungen, Berlin 1867, 48–62.
- ↑ a b Vilkko: „The reception of Frege’s Begriffsschrift“.
- ↑ Siehe z. B. das Stichwort „Ideographie“ in Brockhaus' Kleinem Konversations-Lexikon, 5. Aufl. 1911. (online)
- ↑ Vgl. dazu auch Frege: Funktion und Begriff.
- ↑ a b Frege: Begriffsschrift, S. 5.
- ↑ Frege: Begriffsschrift, S. 24.
- ↑ Vgl. die Fußnote des Herausgebers in der Reprintausgabe, S. 24.
- ↑ Eine Umschrift auch der anderen Sätze in moderne Notation findet sich im Anhang von Richard L. Mendelsohn: The Philosophy of Gottlob Frege.
- ↑ Frege: Begriffsschrift, S. 26.
- ↑ Frege kannte dieses Prinzip aus der 1840 publizierten Leibniz-Schrift Non inelegans specimen demonstrandi in abstractis und zitierte es später in seinen Grundlagen der Arithmetik (1884) in §65: „Eadem sunt, quorum unam potest substitui alteri salva veritate.“
- ↑ Frege: Begriffsschrift, S. 21. Vgl. Kutschera: Gottlob Frege, S. 33f.
- ↑ Kutschera: Gottlob Frege, S. 34.
- ↑ Parsons: On the consistency of the first-order portion of Frege's logical system.
- ↑ Burgess: On a Consistent Subsystem of Frege's Grundgesetze.
- ↑ Vgl. Kutschera: Gottlob Frege, Kap. 6–8.
- ↑ Eine ausführliche Diskussion findet sich in Richard G. Heck: „A Note on the Major Results of Begriffsschrift“
- ↑ Frege: Begriffsschrift, S. 61f., Satz 76.
- ↑ Sluga: „Frege against the Booleans“, S. 80.
- ↑ Diese Aufsätze sind erst in den Nachgelassenen Schriften veröffentlicht.
- ↑ Siehe B. Russell, Principles of Mathematics. (Norton) New York 1903. (Appendix A: The Logical and Arithmatical doctrines of Frege, S. 501 – 521). Englischer Originalwortlaut: „The work of Frege, which appears to be far less known than it deserves, contains many of the doctrines set forth in Parts I and II of the present work …“.
- ↑ Siehe B. Russell, Principles of Mathematics. (Norton) New York 1903: S. 19: „In the scholastic doctrine of the syllogism, and in all previous symbolic logic, the two relations [d.i. eines - Kalküls, dem Enthaltensein und das Teilmengesein ] are confounded, except in the work of Frege“ [Anm. dort zur Begriffsschrift].
- ↑ Siehe dazu oben Abschnitt Stellung der »Begriffsschrift« im Gesamtwerk Freges.
- ↑ K. Gödel, Russells Mathematische Logik. Seite V in: A. N. Whitehead, B. Russell, Principia Mathematica - Vorwort und Einleitungen. Übersetzt von H. Mokre. (Suhrkamp) Frankfurt am Main 1986. Erstveröffentlichung als: The Philosophy of Bertrand Russell. P. Schilpp (Hrsg.), The Library of Living Philosophers (Tudor) New York 1944: S. 125 – 153.
- ↑ Ebenso der folgende Kommentar: „Geht es Frege doch (im Rahmen seines Logizismusprogramms) gerade nicht um eine Mathematisierung der Logik, sondern umgekehrt um eine Logisierung der Mathematik (Arithmetik).“ G. Gabriel, Traditionelle und moderne Logik (2001), hier in der Literatur: S. 22.
- ↑ Ludwig Wittgenstein: Tractatus logico-philosophicus, Vorwort. Zitiert nach der kritischen Ausgabe von Brian McGuinness und Joachim Schulte, Frankfurt am Main 1989, ISBN 978-3-518-28959-4.
- ↑ A. Tarski, Introduction to Logic and to the Methodology of the Deductive Sciences. 1. englische Auflage, Oxford Univ. Press, New York 1941; (Online: Textarchiv – Internet Archive, Abruf am 5. Juli 2024): Seite 19, Anm. 2. Polnische Erstveröffentlichung 1936 unter dem Titel O logice matematycznej i metodzie dedukcyjnej. Der Wortlaut ist der 4. Auflage der deutschen Ausgabe von 1937 entnommen: A. Tarski, Einführung in die mathematische Logik. (Vandenhoeck, Ruprecht) Göttingen 1971: Seite 32 Anm. 2. (Der englische Text wurde hierin eigens wieder von E. Scheibe ins Deutsche übersetzt und neu herausgegeben.)
- ↑ A. Tarski, Einführung in die mathematische Logik. (Vandenhoeck, Ruprecht) Göttingen, 4. Auflage 1971, Seite 92.
- ↑ Siehe dazu vor allen das Standardwerk Donald Monk, Mathematical Logic. (Springer) New York, Heidelberg, Berlin 1976. Online (Open Access): Monk (1976) (Zugriff: 5. Juli 2024). Seite 117 führt Freges Aussagenlogik ein, wobei das hier genannte Axiom 3. dort aus den anderen aussagenlogischen Axiomen deduziert wird, und Axiom 4. tritt in abgewandelter Negationsform auf; Seite 171 führt die Axiome der Prädikatenlogik ein.
- ↑ Siehe dazu Frege: Begriffsschrift, S. VI; §1; §6; §9 und §23.
- ↑ D. Hilbert, W. Ackermann, Grundzüge der theoretischen Logik. 6. Auflage. (Springer) Berlin, Heidelberg, New York 1972. (Erstveröffentlichung 1928): Seite 65 f. (III.1 Unzulänglichkeit des bisherigen Kalküls).
- ↑ Siehe Frege: Begriffsschrift, §22, Nr. 59, 62 und 65.
- ↑ Wolff (1995), hier in der angegebenen Literatur, S. 255 und S. 297, kommentiert Freges Auffassung, dass die hypothetischen Urteile der Kantischen Kategorientafel auf die kategorischen zurückführbar sind, ihr Unterschied ein mehr ‹grammatischer› und weniger ein ‹logischer› sei, wie sich Frege in seinem Vorwort selbst ausdrückt.
- ↑ F. A. Rodriguez-Consuegra, Mathematical Logic and logicism from Peano to Quine, 1890 –1940. § 5.2.3: Frege: The Great Unknown, S. 621 f. In: I. Grattan-Guinness, History & Philosophy of the Mathematical Sciences Vol. 1. (Routledge) London, New York 1994.
- ↑ Siehe G. Gabriel, Traditionelle und moderne Logik (2001), hier in der Literatur: S. 23.
- ↑ Siehe G. Gabriel, Traditionelle und moderne Logik (2001), hier in der Literatur: S. 27. Ebd., S. 23, wird die ‹Art der formalen Strukturierung des Inhaltes› von Urteilen als der wesentliche Unterschied zwischen traditioneller und moderner Logik in Freges Werk gesehen.
- ↑ Siehe auch Wolff (1995), hier in der angegebenen Literatur, S. 276.
- ↑ Frege: Begriffsschrift (1879), § 3 S. 4f.
- ↑ Stephen C. Kleene: Introduction to Metamathematics, Amsterdam u. a. 1952 u. ö., ISBN 978-0-7204-2103-3
- ↑ Arend Heyting: „Die formalen Regeln der intuitionistischen Logik,“ in: Sitzungsberichte der preußischen Akademie der Wissenschaften, phys.-math. Klasse, 1930, S. 42–65.





















![{\displaystyle aR^{\ast }b\equiv \forall F[\forall x(aRx\to F(x))\wedge \forall x\forall y(F(x)\wedge xRy\to F(y))\to F(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7ff07016c36a5960a474fc7e777d9fd692d645)
![{\displaystyle aR^{\ast }b\equiv \forall F[\forall x(aRx\to F(x))\wedge Erbl(F,R)\to F(b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2525b1f5f95c670c57cc4fd4688ddb9fb98af83)























