Biegemoment

Als Biegemoment wird ein Moment bezeichnet, das ein schlankes (Stab, Balken, Welle o. ä.) oder dünnes Bauteil (Platte o. ä.) biegen kann.
Es tritt nicht nur, wie im Bild von den Händen ausgeübt, an den Enden des Bauteils, sondern als Schnittreaktion auch zwischen den Krafteinleitungsstellen auf. Diese Schnittlast bildet eine grundlegende Größe für die Auslegung von schlanken Bauteilen unter Momentenbelastung.[2]:83
Biegemoment in der Balkentheorie[Bearbeiten | Quelltext bearbeiten]

(zur Veranschaulichung ausein.geschnitten)
bei Belastung durch ein Biegemoment (erzeugt durch Kraft F am freien Ende)
Das Verhalten eines schlanken Bauteils bzw. eines Balkens unter Belastung ist Gegenstand der Balkentheorie. Insbesondere wird mithilfe der Festigkeitslehre und der Elastizitätslehre sein Verhalten unter einem ihn belastenden Biegemoment untersucht. Anstatt von der Balkentheorie wird deshalb oft, bzw. im engeren Sinne von der Biegetheorie des Balkens gesprochen.
Das Biegemoment wird beim statisch bestimmten Balken aus den Gleichgewichtsbedingungen hergeleitet. Unter den Annahmen,[2]:43 dass
- alle Punkte eines Querschnitts dieselbe Verschiebung erfahren und die Balkenhöhe unverändert bleibt,
- Querschnitte, die vor der Deformation eben waren, auch danach eben sind, und dass
- Balkenquerschnitte, die vor der Deformation senkrecht auf der Balkenachse standen, auch nach der Deformation senkrecht auf der deformierten Balkenachse stehen
(die letzten beiden sind die Bernoullischen Annahmen[2]:109) können die Biegespannungen im Balkeninneren und die elastische Verbiegung (z. B. Durchbiegung) des Balkens berechnet und mit zulässigen Werten verglichen werden. Coulomb war der erste, der im Rahmen der von ihm 1773 vollendeten Balkentheorie die Biegespannungen zutreffend quantifizierte.[3] Die Biegespannungen sollen kleiner als die für elastische Verformung zulässigen Materialwerte sein (Festigkeitsnachweis gegen plastische Verformung oder Bruch). Gelegentlich liegt eine zusätzliche Anforderung in Form einer zulässigen maximalen Verbiegung vor, die vom errechneten Wert nicht überschritten werden darf.
Die in einem Querschnitt des Balkens aufsummierte Biegespannung ist dem Biegemoment an dieser Stelle proportional. Im Querschnitt verläuft sie von maximaler Druck- am inneren Rand (konkave Biegung) über null in der neutralen Zone zu maximaler Zugspannung am äußeren Rand (konvexe Biegung). Der Festigkeitsnachweis wird i. d. R. mit der maximalen Zugspannung durchgeführt (die von einem Material ertragbare Druckspannung ist i. d. R. größer und damit unkritisch.)
Die Verbiegung des Balkens wird durch seine Krümmung repräsentiert, die an jeder Stelle im Balken proportional zum dort wirkenden Biegemoment ist, wobei der Proportionalitätsfaktor die Biegesteifigkeit des Balkens ist.[2]:104 Die aus der über die Balkenlänge veränderliche Krümmung ermittelte Biegelinie erlaubt eine Aussage über die Einhaltung oder Überschreitung einer zulässigen Durchbiegung.
Beispiele für Biegemoment-Verlauf am Balken[Bearbeiten | Quelltext bearbeiten]

Kragbalken, Einzelkraft am freien Ende[Bearbeiten | Quelltext bearbeiten]
Ein einseitig eingespannter Kragbalken wird am freien Ende im Abstand durch eine Kraft belastet (siehe nebenstehende Abbildung). Der Biegemoment-Verlauf ist
- .
An der Einleitungsstelle () der Kraft ist es null. Bis zur Einspannstelle () steigt es linear auf seinen maximalen Wert .
An den Enden abgestützter Balken, Einzelkraft dazwischen[Bearbeiten | Quelltext bearbeiten]

Zur Berechnung der inneren Momente wird das Bauteil an der interessierenden Stelle gedanklich durchgeschnitten, und es werden diejenigen Momente betrachtet, die an einem Teilstück an seiner Schnittstelle wirken. Das Biegemoment an einer Stelle ist damit die Summe aller Drehmomente, die von Kräften auf einer Seite der Schnittstelle verursacht werden.[4]
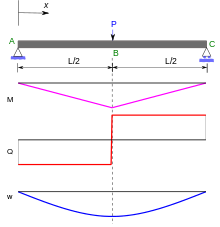
Im an seinen Enden gelagerten Balken mit Einzellast (siehe nebenstehende Abbildung) unterliegt das linke Teilstück einem rechtsdrehenden Drehmoment (in der technischen Mechanik kurz Moment genannt), welches mit Hilfe der Auflagekraft FL am linken Lager beschreibbar ist. Das Moment wächst von null am Auflager linear bis zum Maximalwert an der Stelle der Last F. Rechts davon kommt aus der Last F ein vom Wert null bis zum gleichen Maximalwert am rechten Auflager linear ansteigendes, linksdrehendes Moment hinzu, so dass die Momenten-Summe vom Maximalwert an der Last-Stelle bis null am rechten Ende linear abnimmt.[5]
Im Sonderfall der mittigen Last tritt bei das maximale Biegemoment
auf.
Berechnung des Biegemoments[Bearbeiten | Quelltext bearbeiten]
Die Berechnung des Biegemoments ist besonders einfach, wenn das Bauteil, wie in den Beispielen oben, statisch bestimmt gelagert ist, sodass die Schnittreaktionen aus den Gleichgewichtsbedingungen ableitbar sind. Unter der Voraussetzung, dass nur kleine Verformungen auftreten, kann ihr Einfluss auf die Hebelarme vernachlässigt werden. Bei statisch unbestimmten Problemen oder großen Verformungen müssen alle Gleichungen (Mechanisches Gleichgewicht, Kinematik, Elastizitätsgesetz) gleichzeitig gelöst werden,[2]:14f beispielsweise mit der Finite-Elemente-Methode.
An dieser Stelle wird statische Bestimmtheit bei kleinen Verformungen vorausgesetzt, die in vielen Anwendungen, insbesondere im technischen Bereich, vorliegen. Die Ableitungsfunktion des Biegemoments nach der x-Koordinate in Richtung der Balkenachse liefert den Querkraftverlauf Q:[6]:184
und die zweite Ableitung liefert die Streckenlast q:
Umgekehrt ergibt sich der Biegemomentenverlauf aus der Integration der verteilten Last und der Querkraft.[6]:185 An Stellen, wo
- abrupte Änderungen der verteilten Last (beispielsweise an den Enden ihrer Einwirkung),
- Querkräfte, insbesondere Lagerreaktionen,
- Einzelmomente oder
- Knicke
im Balken auftreten, weist der Momentenverlauf Knicke oder Sprünge auf, vgl. #An den Enden abgestützter Balken, Einzelkraft dazwischen. An diesen Stellen ist das Biegemoment nicht differenzierbar und die Streckenlast bzw. Querkraft nicht integrierbar.
Um obige Formeln trotzdem anwenden zu können, wird der Balken mittels des Schnittprinzips in Stücke zerlegt, in denen keine abrupten Änderungen stattfinden. In diesen Stücken wird das Biegemoment berechnet und mit Hilfe der Übergangsbedingungen an den Rändern zum kompletten Verlauf zusammengesetzt.
Die bereichsweise Integration ist schon bei zwei Feldern mit einigem Aufwand verbunden. Die Arbeit lässt sich jedoch mit der Föppl-Klammer (englisch Macauley Brackets) vereinfachen. Mit ihrer Hilfe können Unstetigkeiten wie Sprünge oder Knicke einfach beschrieben werden.[6]:196 Im Beispiel oben schreibt sich der Querkraftverlauf damit
und der Momentenverlauf
An den Stellen und kann bestätigt werden.
Biegemoment und Biegelinie[Bearbeiten | Quelltext bearbeiten]
Die durch die Biegemoment-Belastung entstehende elastische Verformung wird mit der Biegelinie beschrieben. Für einen Stab konstanten Querschnitts gilt für deren zweite Ableitung:[2]:110
mit
- der Variablen x in Balkenrichtung,
- dem Elastizitätsmodul (eine Materialeigenschaft)
- dem axialen Flächenträgheitsmoment (eine geometrische Größe des konstanten Balken-Querschnitts. Der Index y zeigt an, dass die Biegung um zur x-Achse senkrechten y-Achse erfolgt)
Das Produkt aus Elastizitätsmodul und Flächenträgheitsmoment ergibt die Biegesteifigkeit, die in obiger Formel im Nenner des Bruchs steht.
Die Krümmung der Balkenachse ist durch
gegeben.[2]:110 Bei kleinen Verformungen kann gegenüber der eins im Nenner vernachlässigt werden, sodass wird. Die Krümmung ist damit proportional zum Biegemoment , was z. B. in der nebenstehend abgebildeten Biegelinie erkennbar ist: Das Biegemoment M und die Krümmung sind in der Balkenmitte maximal und an den Enden minimal.
Die Auslenkung der Biegelinie wird durch zweimaliges Integrieren des Krümmungsverlaufs ermittelt, was bei vorhandenen Unstetigkeitsstellen durch die Föppl-Klammer erleichtert wird.
Biegemoment und Biegespannung[Bearbeiten | Quelltext bearbeiten]
Die für den Festigkeitsnachweis zu ermittelnden Biegespannungen in einem Balkenquerschnitt sind dem dort wirkenden Biegemoment , wie in folgender Näherungs-Gleichung für einen Balken mit konstantem Querschnitt angegeben ist, proportional:
- (Variable in Balkenrichtung, Variable in Richtung Balkenhöhe).
Die Proportionalität mit dem Abstand von der neutralen Balkenschicht zeigt an, dass die Biegespannung in den Randschichten am größten ist. Die dort herrschende Biegespannung ist:
- mit (Widerstandsmoment im Balkenquerschnitt gegen Biegung um die y-Achse).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Sogenannte „reine Biegung“ (siehe hier), die selten vorkommt. Meistens liegt „Querkraft-Biegung“ vor: quer auf den Balken wirkt eine mit einer Teillänge des Balkens als Hebelarm multiplizierte Kraft.
- ↑ a b c d e f g D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 2. Elastostatik. Band 2. Springer-Verlag, Heidelberg 2014, ISBN 978-3-642-40965-3, doi:10.1007/978-3-642-40966-0_6 (Der Arbeitsbegriff in der Elastostatik).
- ↑ Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin, ISBN 978-3-433-03229-9, S. 405 ff.
- ↑ Alfred Böge (Hrsg.): Handbuch Maschinenbau: Grundlagen und Anwendungen der Maschinenbau-Technik. 20. Auflage. Springer DE, 2011 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Die von rechts nach links führende Betrachtung führt mit Hilfe der rechten Auflagerkraft FR über ein linksdrehendes Moment zum gleichen Ergebnis.
- ↑ a b c D. Gross, W. Hauger, J. Schröder, W. A. Wall: Technische Mechanik 1. Statik. Springer-Verlag, Heidelberg 2011, ISBN 978-3-642-13805-8, doi:10.1007/978-3-642-13806-5.
































