Diskussion:Kraft
| Auf dieser Seite werden Abschnitte ab Überschriftenebene 2 automatisch archiviert, die seit 7 Tagen mit dem Baustein {{Erledigt|1=--~~~~}} versehen sind. |
| Archiv |
| Wie wird ein Archiv angelegt? |
Die archivierten Diskussionsbeiträge, die sich auf den Stand des Artikels Kraft vor dem Komplettumbau im Juni 2009 bezogen und daher weitestgehend für die aktuelle Diskussion irrelevant sind, befinden sich im ersten Hauptabschnitt des ersten Archivs.
Freischneiden[Quelltext bearbeiten]
Der Abschnitt Freischneiden ist imo völlig daneben. Wenn man einen Körper freischneidet entsteht eine Schnittkraft oder eine Auflagerkraft. Wenn man die Einheit Kraft pro Fläche meint, ist das Ergebnis eine Spannung (Normal- oder Schubspannung). Warum man ausgerechnet ein Volumenkraftbeispiel nimmt um Freischneiden zu erklären bleibt ein Rätsel. Dass F_0 überall sowohl als äußere Kraft und als Schnittkraft ist in der Mechanik unüblich. Eine Schnittkraft wird zunächst mal als Unbekannte angetragen. Dass man einen Körper in "differenziell" kleine Stücke zerschneidet ist Unsinn. Bei FE-Methoden sind's kleine Elemente, beim Freischneiden (analytisch) wird das Schnittufer verschoben. Da sollte mal jemand ran, der sich damit auskennt (ev. Benutzer:JoKalliauer).--Wruedt (Diskussion) 14:16, 3. Jul. 2019 (CEST)
- @Wruedt: Ich konnte im Text keine inhaltlichen Fehler finden, das mache ich aber oft auch erst wenn ich konkrete den Text umschreibe. (In meiner Forschung erklären wir warum die Kontuumsmechanik nicht gilt (ist experimentell bereits von unabhänigen Forschungsgruppen bestätigt und publiziert), mein Chef und mein Dissertationsbetreuer (Professor) geht sogar einen Schritt weiter und sagt, dass das Schnittprinzip gar nicht in der Kontuumsmechanik gilt, insofern könnte ich natürlich mehr kritisieren, es ist eine Frage welches Theorem/Annahmen man für welchen Zweck glauben will.)
- Beim Bild ist die Summe der Vertialkräfte nicht erfüllt.
- „Wenn man einen Körper freischneidet entsteht eine Schnittkraft oder eine Auflagerkraft.“
- Ich würde es anders formulieren, an einer Fläche die man gedanklich freischneidet entsteht eine gedankliche Kraft, die in einer mittleren Traktionsspannung resultiert. Diese Trakionsspannungen aufintegriert ergeben die für die Stabmechanik/Plattenmechnanik relevanten Schnittkräfte und Schnittmomente. Bei Auflagerkräften lässt man diese Schnittfläche (Trennfläche zwischen Objekt und Auflager) im Modell im limes gegen Null gehen und erhält Modell damit auch Einzelkräfte.
- Aufgrund von Gleichgewichtsbetrachtungen kann man oft die Schnittkräfte und Schnittmomente berechnen und daraus die Spannungen im Querschnitt rückschließen.
- „Warum man ausgerechnet ein Volumenkraftbeispiel nimmt um Freischneiden zu erklären bleibt ein Rätsel.“
- Ich gebe dir Recht, dass es nicht sehr relevant ist. Ich vermute die/der AutorIn wollte damit sagen, dass das Eigenengewicht eines homogenen Körpers sich in einem homogegen Feld sich direkt proportional zum freigeschnittenen Volumen verhält.
- „Dass F_0 überall sowohl als äußere Kraft und als Schnittkraft ist in der Mechanik unüblich.“
- Schneide ein System so, dass die Systemgrenze die Schnittgrenze ist und die äußere Kräfte sind Schnittkräfte indente Begriffe. (Wie oben beschrieben geht man in der Kontuumsmechanik üblicherweise davon aus, dass es an der Oberfläche Spannungensrandbediungen oder Verschiebungsrandbediungen gibt. Wenn wir unendlich große Spannungen in der Kontuumsmechanik verhindern wollen, braucht jede Kraft auch eine Fläche auf der sie angreift und somit würde ich, wenn wir nicht nur von Stabtheorie reden eher von äußeren Oberflächenspannungen, anstatt von Kräften sprechen. Bei einer allgemeinen 3D-Kontuumskartofel, die allgmeine 3D-Beanspruchungen hat, macht es IMHO keinen Sinn von Schnittkräften zu reden.)
- Außerdem Nenne F_0 es N und es passt wieder?
- „Dass man einen Körper in "differenziell" kleine Stücke zerschneidet ist Unsinn.“
- Hier ist gemeint, dass man in der Stabmechanik das die Volumenkraft als eine Kraft pro Länge anschreibt, nur eben schlecht formuliert. Wenn du dir Bernoullische_Annahmen#Anwendung durchliest siehst du, dass es Differentialgleichungen sind und die sind immer auf einer infinitesimal kleinen Länge definiert. Man muss z.B: für die Durchbiegung gewisse Therme aufintegrieren.
Textvorschlag:

Behandelt man ein komplexes Problem – wie die mechanischen Wechselwirkungen mehrerer Körper untereinander oder die mechanischen Wirkungen in miteinander verbundenen Körpern (z. B. starre oder deformierbare Körper) – so schneidet man ein relevantes Untersystem gedanklich von seiner Umgebung frei (Schnitt in Verbindungen oder in Körpern selbst). An der Schnittfläche werden anstatt des Kontinuums Spannungs- und Verschiebungsrandbediungen angesetzt. Diese Spannungen werden oft zu Spannungsresultanten zusammengefasst die auch Schnittgrößen genannt werden.
- Ich hab das Gefühl dass @Kein Einstein: die perfekte Person wäre so einen Übersichtsartikel zu schreiben (nur etwas zu eingedeckt), ich bin eher der Detailfreak.
- — Johannes Kalliauer - Diskussion | Beiträge 23:31, 15. Jul. 2019 (CEST)
- @JoKalliauer: Vielen Dank für Deine Kommentare. Zu einigen Punkten. Dein Bild zum Freischneiden ist schon mal wesentlich besser als das aktuelle (Schnittkraft extra bezeichnet, korrekte Symbole z.B. Q für Querkraft). Zur Schnittkraft. Imo erhält man beim Freischneiden eine Schnittkraft. Der Begriff Oberflächenkraft kennzeichnet zwar richtig den Ort des Angriffs (wo soll denn eine Schnittkraft denn sonst angreifen), ist also eine Trivialität. Dass man dabei eine Fläche angeben muss ist erst erforderlich, wenn es um die Spannungen geht. Dass die allseits bekannte Schnittkraft in WP zur Oberflächenkraft umtauft wird grenzt an TF. Differenzielle Schnitte. Auch wenn in die Gleichungen irgend wo dG eingehen sollte, wird der Balken nicht zerschnitten, zumindest ist das seltsam formuliert.
- Der Text wirft mE Spannung und Kraft durcheinander. Da Baustatik nicht zu meinem home-field gehört, würd ich Dich bitten zumindest die größten Unsauberkeiten im Text zu begradigen. Die Streckenlast beim Gewicht hab ich schon geändert. Ansonsten sollte der Abschnitt nicht unbedingt den letzten Stand der Forschung widergeben, sondern die solide Art und Weise wie die Balkenstatik in den Grundsemestern vermittelt wird.--Wruedt (Diskussion) 08:04, 16. Jul. 2019 (CEST)
- @Wruedt:
- „Imo erhält man beim Freischneiden eine Schnittkraft.“
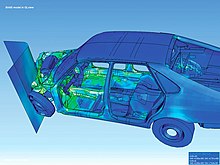
- Man kann auch allgemeine Elemente Freischneiden: File:FAE_visualization.jpg. Hier kann man nicht eine Schnittkraft rechnen und dann die Spannungen rückbestimmen, vielmehr umgekehrt. Also man schneidet frei und setzt stattdessen Spannungen an, diese kann man dann zu einer Schpannungsresultante aufintegrieren, aber hier macht es kaum Sinn Schnittgrößen zu betrachten, Spannungen hingegen schon.
- „Der Begriff Oberflächenkraft kennzeichnet zwar richtig den Ort des Angriffs (wo soll denn eine Schnittkraft denn sonst angreifen), ist also eine Trivialität.“
- Es gibt in der Kontinuumsmechanik,
- Trägheitskraftdichten [N/m³]
- externe Volumenkraftdichten (z.B. zufolge Gravitation oder Magnetismus) [N/m³]
- externe Oberflächenspannungen [N/m²] und
- interne Spannungstensoren [N/m²].
- Also es IMO gibt in der Kontinuumsmechanik vier Arten von Kräften.
- „Dass man dabei eine Fläche angeben muss ist erst erforderlich, wenn es um die Spannungen geht.“

- Den Wasser- und Erddruck bei einer Winkelstützwand wirst man in einer Spannung angeben und nicht als Kraft.
- „Dass die allseits bekannte Schnittkraft in WP zur Oberflächenkraft umtauft wird grenzt an TF.“
- Ich argumentiere mit Hausverstand (TF). Wenn du die Literatur abbilden willst ist @Der-Wir-Ing: der bessere Ansprechpartner. Wir haben sehr konträre Ansetzte, daher ergänzen wir uns meiner Meinung nach(mMn) sehr gut. mMn ist jedoch ein großer Teil der Literatur nur einen für eingeschränkten Bereich (oftmals statisch bestimmte Stabtragwerke) anwendbar. Viele schreiben das in das Vorwort, aber leider unterschlagen das auch viele. Aber Literatur die Freischneiden von allgemeinen 3D-Objekten (z.B. Auto) beschreiben wirst du kaum finden. Jetzt kann man natürlich mit Relevanz argumentieren, aber dann müssen wir auch hineinschreiben das der Abschnitt sich nur auf Stabtragwerke bezieht. (Ist in einem Übersichtsartikel über Kraft ev. zu hinterfragen.)
- „Differenzielle Schnitte. Auch wenn in die Gleichungen irgend wo dG eingehen sollte, wird der Balken nicht zerschnitten, zumindest ist das seltsam formuliert.“
- Beim Schnittprinzip wird der Balken nur gedanklich geschnitten und man kann den gedanklichen Schnitt mit einer Laufvariable x weiterlaufen lassen. Aber ich gebe dir Recht ich würde das raushauen oder bestenfalls auf die DG verweisen.
- „Der Text wirft mE Spannung und Kraft durcheinander.“
- Mein Text oder der derzeitige im Aritel oder beide?
- Es ist ein Henne-Ei-Problem ob zuerst die Kraft da ist und dann eine Spannung daraus resultiert oder ob die Spannung aufintegriert eine Schnittkraft ergibt. Auch wenn man rechnerisch (aufgrund von vereinfachenden Annahmen) sehr schnell eine Schnittkraft berechnen kann und man dann Spannungen rückrechnet, merkt man bei einer Störstelle schnell, dass das nicht möglich ist, daher muss man die inhomogene Spannungsverteilung bestimmen und kann diese zu einer Schnittkraft aufintegrieren, ist mühsamer aber funktioniert "immer". Und Störstellen sind z.B. jeder Knoten der den Anschluss einer Decke an eine Wand darstellt.
- PS. die Literatur bezeichnet mit Traktionskräften Spannungvektoren [N/m²]. Da mache ich mal wirklich TF und bezeiche die Spannungen die lt. Literatur Traktionskräfte heißen als Traktionsspannungen, weil einen Spannungvektor mit Traktionskraft zu bezeichen finde ich irreführend, aber so ist nun mal die Literatur.
„In der französischen und amerikanischen Literatur wird Glg.(1.34) oft ”Tetraeder-Lemma“ genannt. Glg. (1.34) definiert eine Operation, welche die auf drei wechselseitig orthogonal stehende Flächen wirkende Traktionskräfte (Spannungsvektoren) linear (!) mit den Komponenten des Normalenvektors auf eine beliebig ausgerichtete Fläche verknüpft, um den auf diese Fläche wirkenden Spannungsvektor (Traktion) zu quantifizieren.“
@Kein Einstein, JoKalliauer: Dein obiger Textvorschlag ist mit zu allgemein, da nur von Schnittgrößen die Rede ist (ev. Schnittkraft, Schnittmoment). Das Bild ist aber wesentlich besser, da zumindest auch Querkraft und Moment eingezeichnet sind. Beim aktuellen Bild könnte man den Eindruck gewinnen, es handle sich um einen frei fallenden Klotz (s. oben Dein Post Summe der Vertikalkräfte). Trotzdem wird auf die Durchbiegung unter Eigengewicht verwiesen (frag mich was der Abschnitt eigentlich erklären will). Da der Artikel aber Kraft heißt, sollte man imo keine Größen in der Dimension N/m^2 (Spannung, Druck) ins Spiel bringen. Halt mich aber trotzdem raus, ist immerhin (noch) ein lesenswert Artikel. Vielleicht find sich noch jemand der wirklich was davon versteht und textsicher ist.
PS: Zum Auto: Natürlich gibt es an der Barriere Spannungen, die man zu Kräften aufintegieren kann. Das ist beim Reifen der auf der Straße steht nicht anders. Trotzdem wird das ganze als Radlast (N) angegeben, ohne dass man die Fläche des Latsches dabei erwähnt. Die Bemerkung im Text, dass zur Oberflächenkraft auch die Fläche dazu gehört ist unzutreffend.--Wruedt (Diskussion) 09:16, 18. Jul. 2019 (CEST)
- @Wruedt: Textvorschlag

Behandelt man ein komplexes Problem – wie die mechanischen Wechselwirkungen mehrerer Körper untereinander oder die mechanischen Wirkungen in miteinander verbundenen Körpern (z. B. starre oder deformierbare Körper) – so schneidet man ein relevantes Untersystem gedanklich von seiner Umgebung frei (Schnitt in Verbindungen oder in Körpern selbst).An der Schnittfläche werden die innereren Spannungsresultanten durch Schnittkräfte statisch äquivalent ersetzt.Die gedankliche Schnittfläche wird durch Schnittkräfte und Schnittmomente statisch äquivalent ersetzt.
- @Wruedt:Magst du es umschreiben?/einen Textvorschlag machen? Und ja eine Version ohne das Wort Spannungen wäre wohl leichter verständlich. Auch wenn ich vieles an deinen Aussagen kritisiere, finde ich deinen Grundansätze besser als meine eigenen. ;-) — Johannes Kalliauer - Diskussion | Beiträge 22:37, 23. Jul. 2019 (CEST)
- @JoKalliauer:Hatte eigentlich an Dich gedacht, als den hier kompetenteren. Wenn ich das versuchen sollte, würd ich als 1. das Bild rauswerfen, das noch nicht mal das Kräftegleichgewicht in vertikaler Richtung zeigt. Das Beispiel Gewicht ist gut gemeint, aber so kann man das nicht bringen. Gibt's das Bild auch auf WP mit Lizenz? Aber dein Text ist doch gar nicht so schlecht. Bis auf die Spannungsresultanten. Wenn ich mich noch finster an die Vorlesungen zur Balkenstatik erinnere, kommen zuerst die Schnittkräfte, denen man anschließend Spannungen zuordnet. Du nennst das Henne&Ei Problem, und das mag auch je nach Problem in Maschinenbau und Baustatik unterschiedlich gehandhabt werden. Man müsste ev. den Autor des Beitrags befragen, welche Intention damit verbunden war. Den Unterschied Flächenkraft/Volumenkraft kann man auch anders bringen. Was imo nicht geht, ist wie oben schon angemerkt, dass man die allseitsbekannten Schnittkräfte/Schnittmomente in Oberflächenkräfte umtauft. Das war der Ausgang meiner Kritik. Der Begriff Traktionkraft ist imo zu speziell für einen Übersichtsartikel Kraft. Das kann man in Spezialartikeln erwähnen. Der Erddruck müsste auch nicht auftauchen, wenn man sich drauf einigt, dass Kraft die Dimension N hat (siehe Box Physikalische Größe)--Wruedt (Diskussion) 06:57, 24. Jul. 2019 (CEST)
- @Wruedt:Magst du es umschreiben?/einen Textvorschlag machen? Und ja eine Version ohne das Wort Spannungen wäre wohl leichter verständlich. Auch wenn ich vieles an deinen Aussagen kritisiere, finde ich deinen Grundansätze besser als meine eigenen. ;-) — Johannes Kalliauer - Diskussion | Beiträge 22:37, 23. Jul. 2019 (CEST)
- Beim Thema wie Volumenkräfte wirklich in der Balkenstatik berücksichtigt werden bin ich überfragt. Wenn man nicht mehr weiter weiß schmeißt man ein FE-Programm an. Bei Schwingungsphänomenen muss man das ohnehin tun. Aber das gehört doch nicht unter den Abschnitt Freischneiden?--Wruedt (Diskussion) 07:40, 24. Jul. 2019 (CEST)
Dieses unsägliche Bild kam am 14. Juli 2014 rein. Hat fast schon Bestandsschutz. Dass seither kein Fachmann mehr vorbeigekommen ist, kann nur wundern. Für einen lesenswert Artikel machen hier imo eindeutig zu viele Leute rum. Halt mich raus und hoffe dass ein wirklicher Experte wenigstens die gröbsten Klöpse beseitigt, samt aussagekräftigem Bild zum Freischneiden, bei dem der freigeschnittene Klotz wenigstens nicht in Richtung Erdmittelpunkt fällt.--Wruedt (Diskussion) 09:19, 25. Jul. 2019 (CEST)
- @Wruedt: Kann durchaus sein, dass ich inhaltlich kompetenter bin. Aber ich sehe mich eher als den verwirrten Professor, der ist zwar Superkompetent, aber er braucht jemanden der das struturiert, verständlich macht.
- Ja man rechnet in der Stabstatik zuerst Schnittrkäfte und davon Spannungen aus, jedoch in einem 3-D-Kontinuum gibt es keine reale Stabachse und somit keine Schnittkräfte. Von einer Spannungsverteilung kann man eindeutig eine Schnittkraft (mit einer gedachte Achse) bestimmen, umgekehrt geht es jedoch im Allgemeinen nicht, es sei den man geht z.B. von einer homogenen Spannungsverteilung aus und erhält dann eine mittlere Spannung.
- Volumenkraftdichten und Oberflächenspannungen treten in der Kontinuumstheorie auf, jedoch gibt es diese in der Stabstatik genaugenommen nicht. Dafür gibt ein in der Kontinuumstheorie keine Steckenlasten und keine Einzellasten, wie man eine Volumenkraft in eine Streckenlast umrechnet:
- @Wruedt: Kann durchaus sein, dass ich inhaltlich kompetenter bin. Aber ich sehe mich eher als den verwirrten Professor, der ist zwar Superkompetent, aber er braucht jemanden der das struturiert, verständlich macht.
Eine Streckenlast für ein statisches System[1] berechnet sich aus dem Querschnittsintegral der Volumenkraftdichten und dem Oberflächenintegral der Traktionsspannungen:
- mit dem Steckenlastvektor wobei
- die Steckenlastkomponente in -Richtung ist
- die Steckenlastkomponente in -Richtung ist
- die Steckenlastkomponente in -Richtung ist
- mit der Volumenkraftdichte (z. B. Eigenwichte: )
- mit der Querschnittsfläche
- mit der Traktionsspannung (z. B. Oberflächendruck zufolge einer Kontaktkraft mit einem anderen Kontinuum)
- wobei den Normalenvektor darstellt
- mit dem Umfang des Querschnitts
- ↑ Also ein System bei dem in einem Galileischen Bezugssystem keine Beschläunigungskräfte wirken.
Darstellung von Kräften[Quelltext bearbeiten]
Ich dachte, es wäre damit getan, die Beschriftung einer Abbildung zu ändern, jedoch glaube ich inzwischen, dass der Fehler tiefer liegt. Der Textabschnitt lautet:
Die Verformung eines Körpers kommt genau genommen nicht durch eine einzelne Kraft zustande, sondern dadurch, dass an verschiedenen Angriffspunkten im Körper unterschiedliche Kräfte wirken (s. nebenstehende Abbildung). Die dadurch entstehenden mechanischen Spannungen können beschrieben werden, indem Kraft als ein vektorielles Feld aufgefasst wird: In jedem Angriffspunkt, bezeichnet durch den Ortsvektor , kann prinzipiell eine andere Kraft wirken. Je nachdem, wie diese Kräfte gerichtet sind, wird der Körper gedehnt, komprimiert oder verzerrt. Die Krafteinleitung in einen Körper erfolgt genau genommen auch nicht durch eine einzelne Kraft, sondern durch Kräfte in einem vektoriellen Feld bzw. in der Kontaktfläche des Körpers mit einem anderen Körper, über den die Belastung erfolgt.
Die nebenstehende Abbildung ist inkorrekt, weil sie äußere Kräfte mit inneren Spannungen in einer Abbildung darstellen will. Die Darstellung der äußeren Kräfte ist zudem unvollständig, weil die Kräfte am linken Ende des Balkens vollkommen außer acht gelassen werden .
Zum Text: Im ersten Satz ist nicht klar, ob äußere Kräfte oder innere Kräfte gemeint sind. Dann: Die Kraft kann nicht als vektorielles Feld aufgefasst werden. Vielmehr gilt . Es ist die Spannung, nicht die Kraft, die ein Vektorfeld ist. (Wäre das nicht so, dann würden zwei unmittelbar benachbarte Flächenelemente sofort zu einer Verdopplung der Kraft führen (was absurd ist). Schließlich kann man sich fragen, ob der ganze kritisierte Abschnitt nicht eh offtopic ist, weil er ja nicht über Kräfte schreibt, sondern über Spannungen.--Pyrrhocorax (Diskussion) 14:47, 9. Jul. 2019 (CEST)
- Info: In der lesenwerten Version und noch einige Jahre danach stand
Die Verformung eines Körpers kommt genau genommen nicht durch eine einzelne Kraft zustande, sondern dadurch, dass an verschiedenen Angriffspunkten unterschiedliche Kräfte wirken. Solche mechanische Spannungen können beschrieben werden, indem Kraft als ein vektorielles Feld aufgefasst wird: In jedem Angriffspunkt, bezeichnet durch den Ortsvektor , kann prinzipiell eine andere Kraft herrschen. Je nachdem, wie diese Kräfte gerichtet sind, wird der Körper gedehnt, komprimiert oder verzerrt.
- Was imho sicher erhaltenswert ist, ist eine Anmerkung dazu, dass "eine Kraft alleine" nichts verformt.
- <quetsch> Das gilt für den statischen Fall. Oder man muss bei Beschleunigung die Trägheitskräfte mitzählen.--Bleckneuhaus (Diskussion) 17:30, 9. Jul. 2019 (CEST)<quetsch\>
- Was auch seinen Platz im Artikel haben sollte, ist der Bezug von Kraft und Spannung. Hier aufgrund missratener Formulierungen gleich alles zu streichen fände ich ein wenig das Kind mit dem Bade ausgeschüttet.
- Eine Ursache dieser ganzen Schräglage: Die Positionierung im Abschnitt "Darstellung" kommt daher, dass es solche Darstellungen wie im Kragträger-Bild gibt und es hilfreich wäre, den Bezug zu Kraft-Darstellungen klarzustellen. Dieser Ort passt aber eher nicht zu Ausführungen zur mechanischen Spannung, die eher als eigener Punkt nach "Zusammenhang von Kraft und Drehmoment" gehörte.
- Newtopic: Was ich gerne mal lesen würde wäre ein zusammenhängender Überblick über die verschiedenartige Herangehensweise (nebst Hintergrund) und die teilweise recht andersartige Darstellung der (vereinfachend so genannten) Ingenieure vs. uns Physiker - inklusiver solcher Formulierungen wie "Krafteinleitung". Aber das kann wohl nur jemand gut darstellen, der in beiden Welten gleichermaßen zuhause ist. Kein Einstein (Diskussion) 15:52, 9. Jul. 2019 (CEST)
- "jemand [...] der in beiden Welten gleichermaßen zuhause ist." Nunja, ich hab zwei Semester lang Technische Mechanik studiert und ein paar Jahre später Bücher zur Theoretischen Mechanik gelesen. --DWI 17:41, 9. Jul. 2019 (CEST)
- Zwei Semester TM ist nicht viel. Entscheidend zum fähigen Mitreden ist aber, es auch verstanden zu haben. Und grade bei Kollegen die damit argumentieren „etwas gelesen“ zu haben ist das sehr häufig nicht der Fall. --91.47.26.178 10:38, 10. Jul. 2019 (CEST)
- "jemand [...] der in beiden Welten gleichermaßen zuhause ist." Nunja, ich hab zwei Semester lang Technische Mechanik studiert und ein paar Jahre später Bücher zur Theoretischen Mechanik gelesen. --DWI 17:41, 9. Jul. 2019 (CEST)
Kraft als Energieverbrauch[Quelltext bearbeiten]
Trotz des sehr umfangreichen Artikels fehlt dieser Zusammenhang (oder habe ich etwas überlesen?). Jeder streckenspezifische Energieverbrauch hat die Dimension der Kraft, da W = F x s, gilt : F = W/s. D.h. z. B. lässt sich der Verbrauch eines Elektroautos/ebikes mit der sperrigen einheit kWh/100km ganz leicht in die Einheit Newton umrechnen = 3600 W sec/100 m = 36 N.
Wenn ich also ein mit 36 N also einer gefühlten Kraft von ca. 3,6 kg mein E-bike schiebe, um alle Reibkräfte (incl Luft) entgegen zu wirken, habe ich einen Verbrauch von 1kWh/100km und mit einem 500Wh Akku komme ich 50 km weit, das ist realistisch (habe ein S-Pedec).
D.h. ein Auto mit 20 kWh/100km schiebt im Schnitt mit 720 N also gefühlte 72 kg.
Ich finde den Zusammenhang sollte man einfügen. --Zwölfvolt (Diskussion) 17:34, 11. Jul. 2020 (CEST)
- Hmm, könnte passen. Schreib doch einen Vorschlag. Fürs erste einen verwirrenden Tippfehler ausgebessert (kW => kWh). --Bleckneuhaus (Diskussion) 18:05, 11. Jul. 2020 (CEST)
- Ich halte diese (für mich ungewöhnliche) Perspektive auf die Effizienz von Fahrzeugen für interessant. Allerdings sehe ich nicht, wie man das passend in den Artikel Kraft einbauen kann. Die Deutung des Ergebnisses als mittlere Schubkraft bzw. Als Summe aller zu überwindenden Widerstände ist imho jeweils nicht wirklich tragfähig - was aber soll hier dann geschrieben werden?
- Zweiter Aspekt: Soll auch im Artikel Fläche etwas zum Spritverbrauch (Liter / 100 km --> Dimension Fläche...) geschrieben werden und so weiter? Kein Einstein (Diskussion) 08:10, 12. Jul. 2020 (CEST)
- Ja, die Kraft als Energie pro Weg beim Fahrzeugschieben ist anschaulich. Aber Vorsicht: nicht immer bedeutet gleiche Dimension zweier Größen "das ist eigentlich dasselbe wie". Beispiel: Drehimpuls und Wirkung (Physik). --UvM (Diskussion) 10:58, 12. Jul. 2020 (CEST)
- Der Spritverbrauch ergibt sich ja nicht nur aus der Überwindung der Widerstände, sondern leider auch durch den Wirkungsgrad der thermischen Prozesse etc. Zum Spritverbrauch sollte man sich imo im Artikel nicht auslassen.--Wruedt (Diskussion) 11:10, 12. Jul. 2020 (CEST)
- Ja, die Kraft als Energie pro Weg beim Fahrzeugschieben ist anschaulich. Aber Vorsicht: nicht immer bedeutet gleiche Dimension zweier Größen "das ist eigentlich dasselbe wie". Beispiel: Drehimpuls und Wirkung (Physik). --UvM (Diskussion) 10:58, 12. Jul. 2020 (CEST)
Unangemessener Untertitel in Android App[Quelltext bearbeiten]
In der Android App, in der Browserversion unsichtbar, befindet sich ein Untertitel zu diesem Artikel mit beleidigenden Inhalt. Leider gelingt es mir nicht, ihn zu editieren (Bug, fehlende Rechte?). --Svenmk (Diskussion) 12:04, 21. Jan. 2023 (CET)
- Sehr rätselhaft, wie das vor Änderungen gesichert ist. Selbst [1] hilft nicht weiter. Wer dann sonst??? --Bleckneuhaus (Diskussion) 12:50, 21. Jan. 2023 (CET)
- Prüfe bitte, ob das noch zu sehen ist. Ich meine, es müsste nun weg sein - oder? Kein Einstein (Diskussion) 14:00, 21. Jan. 2023 (CET)
- @Kein Einstein ich sehe es leider noch. auch nach manuellem Update der Seite. --Svenmk (Diskussion) 14:14, 21. Jan. 2023 (CET)
- @Svenmk: Mist, ich dachte, es wäre gleich nach deiner Meldung erledigt. Nun besser? Erstaunlicherweise ist der Vandalismus auf Wikidata seit Tagen revertiert ... Kein Einstein (Diskussion) 14:18, 21. Jan. 2023 (CET)
- Das wurde am 15. Januar eingefügt und am 16. entfernt [2] Es liegt nicht an uns. Da müsste mal jemand seinen chache leeren. Man kann sich die mobile Beschreibung auch anzeigen lassen, wenn man was in seine commons.css packt [3] --Der-Wir-Ing ("DWI") (Diskussion) 14:30, 21. Jan. 2023 (CET)
- @Der-Wir-Ing: Das Seltsame war, dass ich es auch noch gesehen habe, nachdem ich es zweimal überschrieb. Nun, nach Veränderung des Wortlautes der Beschreibung, scheint es sofort weg zu sein. Kein Einstein (Diskussion) 14:37, 21. Jan. 2023 (CET)
- @Kein Einstein super, ich sehe es jetzt auch nicht mehr. danke an alle! --Svenmk (Diskussion) 14:41, 21. Jan. 2023 (CET)
- Ich hab die mobile Version gepurged, vielleicht hat das geholfen. --Der-Wir-Ing ("DWI") (Diskussion) 14:46, 21. Jan. 2023 (CET)
- @Kein Einstein super, ich sehe es jetzt auch nicht mehr. danke an alle! --Svenmk (Diskussion) 14:41, 21. Jan. 2023 (CET)
- @Der-Wir-Ing: Das Seltsame war, dass ich es auch noch gesehen habe, nachdem ich es zweimal überschrieb. Nun, nach Veränderung des Wortlautes der Beschreibung, scheint es sofort weg zu sein. Kein Einstein (Diskussion) 14:37, 21. Jan. 2023 (CET)
- @Kein Einstein ich sehe es leider noch. auch nach manuellem Update der Seite. --Svenmk (Diskussion) 14:14, 21. Jan. 2023 (CET)
- Prüfe bitte, ob das noch zu sehen ist. Ich meine, es müsste nun weg sein - oder? Kein Einstein (Diskussion) 14:00, 21. Jan. 2023 (CET)
Abartig viel Text[Quelltext bearbeiten]
Individueller Eindruck das das wie ein verdammter Roman wirkt. Wird man geradezu erschlagen von bergen an text. Sehr unangenehm --Lstein83 (Diskussion) 21:58, 7. Mär. 2023 (CET)
- Dein Unbehagen ist für mich nachvollziehbar. Aber was kann man machen, wenn eine Enzyklopädie entstehen soll (lies das mal, Einleitung genügt schon). Ist halt kein Lehrbuch, wo didaktische Zielrichtung viel wesentlicher ist. --Bleckneuhaus (Diskussion) 23:04, 7. Mär. 2023 (CET)

















