Geometrische Reihe

Die geometrische Reihe $\sum _{k=0}^{\infty }r^{k}$ für $r={\tfrac {1}{2}}$, $r={\tfrac {1}{3}}$ oder $r={\tfrac {1}{4}}$ konvergiert

Eine geometrische Reihe ist die Reihe einer geometrischen Folge. Bei einer geometrischen Folge $(a_{n})$ ist der Quotient $q$ zweier benachbarter Folgenglieder konstant:

$a_{n+1}=a_{n}q$

Das bedeutet, dass die Folgenglieder bezüglich des Summenindex einen Exponentiellen Verlauf annehmen.

Die Folgenglieder der zugehörigen geometrischen Reihe ergeben sich aus den Summenabschnitten:

$s_{n}=a_{1}+a_{1}q+a_{1}q^{2}+\ldots +a_{1}q^{n-1}$

$=a_{1}(1+q+q^{2}+\ldots +q^{n-1})$

Also verhält sich der vom Summenindex abhängige Exponent in den Folgegliedern bezüglich des Summenindex linear.

Grundlegende Form

Divergenter Fall

Ein Quotient $q\geq 1$ ergibt eine divergente geometrische Reihe, z. B. für $q=2$ und Startwert $1$

$1,1+2,1+2+4,1+2+4+8,\dots$ zusammengefasst also $1,3,7,15,\dots$

Im Falle der hier abgebildeten Zweierpotenzen erscheinen stets die Mersenneschen Zahlen als Werte der Summe.

Und der Grenzwert der Mersenneschen Zahlen gegen den Index Unendlich nimmt die Zahl Plus Unendlich an.

Konvergenter Fall

Für $|q|<1$ konvergiert die geometrische Reihe hingegen; es gilt in diesem Fall

$\sum _{k=0}^{\infty }q^{k}=1+q+q^{2}+\dots ={\frac {1}{1-q}}$

Denn an der Summenkette ist folgendes Kriterium direkt erkennbar:

Wenn vom Wert der unendlichen Summe die Zahl eins abgezogen wird, dann entsteht das q-Fache von diesem Wert:

${\biggl (}\sum _{k=0}^{\infty }q^{k}{\biggr )}-1=q\,{\biggl (}\sum _{k=0}^{\infty }q^{k}{\biggr )}$

Daraus folgt sofort, dass dieser Wert gleich dem Kehrwert von der Differenz 1 - q sein muss.

Bei identischem Startwert 1 und einem Quotienten von ¹⁄₂ ergibt sich zum Beispiel: 1, 1 + ¹⁄₂, 1 + ¹⁄₂ + ¹⁄₄, 1 + ¹⁄₂ + ¹⁄₄ + ¹⁄₈, …, also 1, ³⁄₂, ⁷⁄₄, ¹⁵⁄₈, … mit dem Grenzwert ${\tfrac {1}{1-1/2}}=2$.

Für die Reihen gilt die Festlegung $0^{0}:=1$, die im Zusammenhang mit Potenzreihen üblich ist und welche auf der Kenntnis des folgenden Grenzwertes hervorkommt:

$\lim _{a\rightarrow 0}a^{a}=1$

Auf der Regel von de L’Hospital basiert dieser Grenzwert.

Berechnung der (endlichen) Partialsummen einer geometrischen Reihe

Eine Reihe ist per Definition eine Folge von Partialsummen. Der Wert der Reihe ist der Grenzwert dieser Folge von Partialsummen. Eine endliche Summe ist somit ein Folgenglied aus der Folge der Partialsummen. Die (endliche) Summe der ersten $n$ Glieder einer Reihe bezeichnet man also als $n$-te Partialsumme und nicht etwa als „Partialreihe“ o. ä.

Gegeben sei eine geometrische Folge $(a_{k})_{k\in \mathbb {N} _{0}}$.

$s=\sum _{k=0}^{\infty }a_{k}$

ist der Grenzwert der zugehörigen geometrischen Reihe.

Wir können daraus eine neue Folge

$(s_{n})=\left(\sum _{k=0}^{n}a_{k}\right)=\left(\sum _{k=0}^{0}a_{k},\sum _{k=0}^{1}a_{k},\sum _{k=0}^{2}a_{k},\sum _{k=0}^{3}a_{k},\dotsc \right)=\left(a_{0},a_{0}+a_{1},a_{0}+a_{1}+a_{2},a_{0}+a_{1}+a_{2}+a_{3},\dotsc \right)$

konstruieren, deren $n$-tes Glied jeweils die Summe der ersten $n$ Glieder der Reihe $s$ ist, die sogenannte $n$-te Partialsumme von $s$. Diese Folge heißt die Folge der Partialsummen zu $s$. (Genau genommen wird in umgekehrter Reihenfolge die Reihe auf Grundlage von Partialsummen einer Folge definiert. Die obige und übliche Schreibweise für die Reihe gibt das aber nicht her, deshalb müssen wir aus ihr erst die Folge der Partialsummen rekonstruieren.) Falls sie konvergiert, wird über sie der Wert der Reihe $s$ definiert. Es gilt für den Wert der Reihe $s$ (hier wird nicht mehr von „Grenzwert“ gesprochen):

$s:=\lim _{n\to \infty }s_{n};$

in Worten: Der Wert der Reihe $s$ ist definiert als der Grenzwert der zu ihr gehörigen Partialsummen-Folge, falls diese konvergiert, andernfalls wird die Reihe als divergent bezeichnet. Falls in diesem Falle die Folge der Partialsummen gegen (plus / minus) Unendlich strebt, schreibt man gewöhnlich $s=\lim _{n\to \infty }s_{n}=\infty$ oder ${-}\infty$ und sagt, die Folge konvergiere gegen den uneigentlichen Grenzwert (plus / minus) Unendlich oder die Reihe habe den uneigentlichen Wert (plus / minus) Unendlich. (Eine Berechnungsformel für den Grenzwert folgt weiter unten.)

Mit $q$ bezeichnen wir nun das Verhältnis $a_{k+1}/a_{k}$ zweier benachbarter Glieder, das für alle $k$ gleich ist.

Dann gilt $a_{k}=a_{0}q^{k}$ für alle $k$.

Für die $n$-te Partialsumme $s_{n}$ ergibt sich damit:

$s_{n}=a_{0}\sum _{k=0}^{n}q^{k}$

Wenn $q\neq 1$, dann gilt (Herleitung siehe unten)

$s_{n}=a_{0}{\frac {q^{n+1}-1}{q-1}}=a_{0}{\frac {1-q^{n+1}}{1-q}}$

Falls $q=1$, so gilt

$s_{n}=a_{0}(n+1)$

Das Obige gilt, wenn die Folgenglieder Elemente eines unitären Ringes sind, also insbesondere, wenn es reelle Zahlen sind.

Verwandte Summenformeln

Endliche Summenformeln

• Die Partialsumme

$s_{n}=a_{0}\sum _{k=0}^{n}q^{k}k$

hat für $q\neq 1$ das Ergebnis

$s_{n}=a_{0}{\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(q-1)^{2}}}$

und für $q=1$ (vgl. Gaußsche Summenformel)

$s_{n}=a_{0}\sum _{k=0}^{n}1^{k}k=a_{0}\sum _{k=0}^{n}1k=a_{0}\sum _{k=0}^{n}k=a_{0}{\frac {n(n+1)}{2}}$; Die so entstehenden Werte $s_{n}\div a_{0}$ werden Dreieckszahlen genannt.

Diese Formel ergibt sich auch aus der Formel für $q\neq 1$ (mit zweifacher Anwendung der Regel von de L’Hospital) als deren Grenzwert für $q\to 1$.

• Die Partialsumme

$s_{n}=a_{0}\sum _{k=0}^{n}q^{k}k^{2}$

hat für $q\neq 1$ das Ergebnis

$s_{n}=a_{0}{\frac {n^{2}q^{n+3}-(2n^{2}+2n-1)q^{n+2}+(n+1)^{2}q^{n+1}-q^{2}-q}{(q-1)^{3}}}$

und für $q=1$ (vgl. Potenzsummen)

$s_{n}=a_{0}{\frac {n(n+1)(2n+1)}{6}}$

Die auf die nun genannte Weise entstehenden Werte $s_{n}\div a_{0}$ werden Quadratische Pyramidalzahlen genannt.

Die Dreieckszahlen und die Quadratischen Pyramidalzahlen bilden die ersten Spezialfälle zu den Faulhabersche Formeln, welche von Donald Knuth und Johannes Faulhaber erforscht wurden.

Beispiele

Zahlenbeispiel

Gegeben sei die geometrische Folge

$a_{0}=5,\ a_{1}=15,\ a_{2}=45,\ a_{3}=135,\ \dotsc$

mit $a_{0}=5$ und $q=3.$ Die zugehörige geometrische Reihe ist

$s=5\sum _{k=0}^{\infty }3^{k}=\sum _{k=0}^{\infty }5\cdot 3^{k}=5+15+45+135+\dotsb =\infty$

Die zugehörige Folge von Partialsummen ergibt sich zu

$s_{0}=5=5{\frac {1-3^{1}}{1-3}}$

$s_{1}=5+15=20=5{\frac {1-3^{2}}{1-3}}$

$s_{2}=5+15+45=65=5{\frac {1-3^{3}}{1-3}}$

$s_{3}=5+15+45+135=200=5{\frac {1-3^{4}}{1-3}}$

usw.

Geometrische Veranschaulichungen

Figur 1

Figur 2

Zur Summenformel

Das große gleichseitige Dreieck $ABC$, dessen Flächeninhalt ohne Beschränkung der Allgemeinheit als $1$ angenommen wird, setzt sich aus drei flächengleichen unendlichen Folgen gleichseitiger Dreiecke (rot, gelb, blau) zusammen, deren Grenzwerte jeweils ${\tfrac {1}{3}}$mal so groß sind wie das Dreieck $ABC$ (Figur 1). Wegen der Selbstähnlichkeit der Dreiecke $ABC$, $A_{1}B_{1}C$, $A_{2}B_{2}C$, … und ihrer Mittendreieck-Eigenschaften besitzt jede der drei Dreiecksfolgen den Grenzwert

$\sum _{k=1}^{\infty }\left({\frac {1}{4}}\right)^{k}$.

Also gilt

$\sum _{k=1}^{\infty }\left({\frac {1}{4}}\right)^{k}={\frac {1}{3}}$.

Zu einer verwandten Summenformel

In Figur 2 gilt:

$1+2\cdot {\frac {1}{2}}+3\cdot {\frac {1}{4}}+4\cdot {\frac {1}{8}}+5\cdot {\frac {1}{16}}+\ldots =4$.

Dies bestätigt die Partialsummenformel

$s_{n}=a_{0}\sum _{k=0}^{n}q^{k}k$

für $a_{0}=2$, $q={\frac {1}{2}}$ und $n=5$.

Rentenrechnung

Angenommen, man zahlt am Anfang eines jeden Jahres 2000 € bei einer Bank ein und die Zinsen liegen bei 5 % [d. h. der Zinsfaktor ist: $1+(5/100)=1{,}05$]. Wie viel Geld hat man am Ende des fünften Jahres?

Das im ersten Jahr eingezahlte Geld wird fünf Jahre lang verzinst, man erhält dafür am Ende inklusive Zinseszins 2000 · 1,05⁵ €. Das im zweiten Jahr eingezahlte Geld wird nur noch vier Jahre verzinst und so weiter. Insgesamt ergibt sich dann durch die Rentenrechnung ein angesparter Betrag von

${\begin{aligned}&2\,000\cdot 1{,}05^{5}+2\,000\cdot 1{,}05^{4}+2\,000\cdot 1{,}05^{3}+2\,000\cdot 1{,}05^{2}+2\,000\cdot 1{,}05^{1}\\&\quad =2\,000\cdot 1{,}05\cdot (1{,}05^{4}+1{,}05^{3}+1{,}05^{2}+1{,}05^{1}+1{,}05^{0})\\&\quad =2\,000\cdot 1{,}05\cdot \sum _{k=0}^{4}1{,}05^{k}\\&\quad =2\,000\cdot 1{,}05\cdot {\frac {1{,}05^{4+1}-1}{1{,}05-1}}\\&\quad =2\,000\cdot 1{,}05\cdot {\frac {1{,}05^{5}-1}{0{,}05}}\\&\quad =11\,603{,}826\end{aligned}}$

Durch Zinsen hat sich das Kapital somit um 1603,83 € erhöht. Beim Nachrechnen von Kontoauszügen ist zu bedenken, dass im Bankenwesen nicht mathematisch gerundet wird.

Zum Vergleich: Würden nicht Jahr für Jahr je 2000 € eingezahlt, sondern gleich von Beginn an die ganzen 10000 € über 5 Jahre bei 5 % Zinsen angelegt, so wäre der Endbetrag

$10\,000\cdot 1{,}05^{5}=12\,762{,}8156$

also ein Kapitalertrag von 2762,82 €.

Allgemein gilt: Beträgt die Einlage am Anfang jedes Jahres $a_{0}$, der Zinsfaktor $q$ und die Laufzeit $n$ Jahre, dann ist der Endwert

$a_{0}\sum _{k=1}^{n}q^{k}=a_{0}q{\frac {q^{n}-1}{q-1}}$.

Rentenrechnung mit linearer Dynamik

Zahlt man im Gegensatz zum vorigen Beispiel nicht jährlich einen festen Beitrag $a_{0}$, sondern ab dem 2. Jahr jedes Jahr $d$ mehr als im Vorjahr (lineare Dynamik) ein, so ist der Endwert

${\begin{aligned}&\sum _{k=1}^{n}q^{k}(a_{0}+d(n-k))=\sum _{k=1}^{n}(q^{k}(a_{0}+dn)-q^{k}dk)\\&\qquad =\left(\sum _{k=1}^{n}q^{k}(a_{0}+dn)\right)-\left(\sum _{k=1}^{n}q^{k}dk\right)\\&\qquad =(a_{0}+dn)\left(\sum _{k=1}^{n}q^{k}\right)-d\left(\sum _{k=1}^{n}q^{k}k\right)\\&\qquad =(a_{0}+dn){\frac {q^{n+1}-q}{q-1}}-d{\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(q-1)^{2}}}\end{aligned}}$

zum Beispiel mit $a_{0}=2.000$ € im ersten Jahr, jedes Jahr $d=100$ € mehr als im Vorjahr, 5 % Zinsen (also Zinsfaktor $q=1{,}05$) und $n=5$ Jahren Laufzeit, dann ist der am Ende des 5. Jahres angesparte Betrag

${\begin{aligned}&(2\,000+100\cdot 5)\cdot {\frac {1{,}05^{5+1}-1{,}05}{1{,}05-1}}-100\cdot {\frac {5\cdot 1{,}05^{5+2}-(5+1)\cdot 1{,}05^{5+1}+1{,}05}{(1{,}05-1)^{2}}}\\&\qquad =2\,500\cdot {\frac {0{,}29}{0{,}05}}-100\cdot {\frac {7{,}03-8{,}04+1{,}05}{0{,}0025}}\\&\qquad =2\,500\cdot 5{,}8-100\cdot {\frac {0{,}0449}{0{,}0025}}\\&\qquad =14\,504{,}78-100\cdot 17{,}97\\&\qquad =12\,707{,}65\end{aligned}}$

wobei in diesem Beispiel nicht 10.000 €, sondern insgesamt 11.000 € eingezahlt wurden, also beträgt der Gewinn 1.707,65 €. Zahlt man statt $a_{0}=2.000$ € im ersten Jahr nur $a_{0}=1.800$ € ein und lässt die anderen Faktoren gleich (sodass man wie im vorletzten Beispiel insgesamt 10.000 € einzahlt), dann ist der Endwert nur noch 11.547,27 €, das heißt zahlt man den gleichen Betrag ein, nur zu Beginn weniger, dafür später mehr, dann entgehen einem Gewinne (Opportunitätskosten).

Periodische Dezimalbrüche

Periodische Dezimalbruchentwicklungen enthalten eine geometrische Reihe, welche mit den obigen Formeln wieder in einen Bruch umgewandelt werden kann.

Beispiel 1:

${\begin{aligned}0{,}2{\overline {67}}&={\frac {2}{10}}+{\frac {67}{1000}}\cdot \sum _{k=0}^{\infty }\left({\frac {1}{100}}\right)^{k}={\frac {2}{10}}+{\frac {67}{1000}}\cdot {\frac {1}{1-{\frac {1}{100}}}}\\&={\frac {2}{10}}+{\frac {67}{1000}}\cdot {\frac {100}{99}}={\frac {2}{10}}+{\frac {67}{990}}={\frac {265}{990}}={\frac {53}{198}}\end{aligned}}$

Beispiel 2:

$0{,}{\overline {9}}={\frac {9}{10}}+{\frac {9}{100}}+{\frac {9}{1000}}+\dotsb ={\frac {9}{10}}\cdot \sum _{k=0}^{\infty }\left({\frac {1}{10}}\right)^{k}={\frac {9}{10}}\cdot {\frac {1}{1-{\frac {1}{10}}}}={\frac {9}{10}}\cdot {\frac {10}{9}}=1$

Achilles und die Schildkröte

Ein sehr anschauliches Beispiel für die Anwendung (und sogar Herleitung des Grenzwerts) der geometrischen Reihe ist Geschichte von Achilles und der Schildkröte.

Der für seine Schnelligkeit bekannte Athlet Achilles tritt in einem Wettlauf gegen eine langsame Schildkröte an. Beide starten zum selben Zeitpunkt, aber die Schildkröte erhält anfangs einen Vorsprung von, zum Beispiel $100\,{\text{m}}$. Obwohl Achilles mit einer um den Faktor $p$, mit $p>1$, höheren Geschwindigkeit als die der Schildkröte läuft, kann er sie scheinbar niemals einholen. Denn: Sobald Achilles $100\,{\text{m}}$ weit gelaufen ist, also den Punkt erreicht hat, an dem die Schildkröte gestartet ist, ist eine gewisse Zeit verstrichen. In dieser Zeit hat die Schildkröte die Strecke $100\,{\text{m}}/p$ zurückgelegt. Achilles muss also die entsprechende Strecke weiterlaufen, um die Schildkröte einzuholen. Derweil hat die Schildkröte jedoch weitere $100\,{\text{m}}/p^{2}$ zurückgelegt. Achilles hat die Schildkröte immer noch nicht eingeholt. Er läuft entsprechend weiter, muss nun allerdings feststellen, dass die Schildkröte in der Zwischenzeit abermals eine gewisse Strecke zusätzlich zurückgelegt hat; dieses Mal sind es $100\,{\text{m}}/p^{3}$. Dieses Spiel setzt sich unendlich oft fort.

Der Punkt $x$, an welchem Achilles die Schildkröte endlich einholen wird, ist gegeben durch die unendliche Summe

$x=100\,{\text{m}}+{\frac {100\,{\text{m}}}{p}}+{\frac {100\,{\text{m}}}{p^{2}}}+{\frac {100\,{\text{m}}}{p^{3}}}+\dots =100\,{\text{m}}\sum _{k=0}^{\infty }p^{-k}.$

Alternativ können wir $x$ durch das Aufstellen zweier linearer Gleichungen bestimmen. Es seien

${\begin{aligned}x_{\text{S}}(t)&=v\,t+100\,{\text{m}}\quad {\text{bzw.}}\\x_{\text{A}}(t)&=p\,v\,t\end{aligned}}$

die Bewegungsgleichungen der Schildkröte bzw. von Achilles, wobei $v$ die Geschwindigkeit der Schildkröte und $t$ die verstrichene Zeit ist. Wir suchen nun die $x$-Koordinate des Schnittpunkts von $x_{\text{S}}(t)$ und $x_{\text{A}}(t)$. Durch Gleichsetzen beider Gleichungen, Umformung auf $t$ und Einsetzen von $t$ in eine der beiden Gleichungen erhalten wir $x=100\,{\text{m}}/(1-1/p)$. Der Wert ist endlich; Achilles wird die Schildkröte also doch einholen. Vergleichen wir diese Lösung mit derjenigen von oben, so finden wir

${\begin{aligned}100\,{\text{m}}\sum _{k=0}^{\infty }p^{-k}={\frac {100\,{\text{m}}}{1-(1/p)}},\quad {\text{oder äquivalent}}\quad \sum _{k=0}^{\infty }q^{k}={\frac {1}{1-q}},\end{aligned}}$

wobei im letzten Schritt auf beiden Seiten durch $100\,{\text{m}}$ geteilt und die Variable $q:=1/p$, mit $0<q<1$, eingeführt wurde.

Konvergenz und Wert der geometrischen Reihe

Konvergenz der geometrischen Reihe für $q={\tfrac {1}{2}}$

Konvergenz der geometrischen Reihe auf der Zahlengeraden

$\sum _{k=0}^{\infty }r(1-r)^{k}=1$ ($0<r<1$)

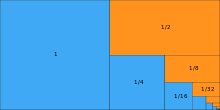
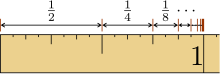
Eine geometrische Reihe bzw. die Folge ihrer Partialsummen konvergiert genau dann, wenn der Betrag der reellen (oder komplexen) Zahl $q$ kleiner als Eins oder ihr Anfangsglied $a_{0}$ gleich Null ist. Für $|q|<1$ oder $a_{0}=0$ konvergiert die zugrundeliegende geometrische Folge nämlich gegen Null:

$\lim _{k\to \infty }a_{0}q^{k}=0$.

Nach dem Nullfolgenkriterium ist dies eine notwendige Bedingung für die Konvergenz der geometrischen Reihe. Da für $|q|>1$ und $a_{0}\neq 0$ die Grundfolge divergiert, liegt in diesem Falle somit auch Divergenz der Reihe vor.

Für $q=1$ ergibt sich die Divergenz der geometrischen Reihe aus

$\sum _{k=0}^{N}a_{0}q^{k}=\sum _{k=0}^{N}a_{0}\cdot 1=(N+1)\cdot a_{0}$,

ein Ausdruck, der für $N\to \infty$ und $a_{0}\neq 0$ divergiert.

Für den Fall $q>1$ ergibt sich die Divergenz immer als bestimmte Divergenz (s. o.), für den Fall $q\leq -1$ immer als unbestimmte Divergenz. Die geometrische Reihe konvergiert auch absolut, sofern sie auf normale Weise konvergiert.

Der Wert der Reihe im Konvergenzfall ergibt sich aus jener obenstehenden Formel für die $n$-ten Partialsummen durch Grenzwertbildung ($n\to \infty$) für $|q|<1$ zu

$\sum _{k=0}^{\infty }a_{0}q^{k}=\lim _{n\to \infty }\sum _{k=0}^{n}a_{0}q^{k}=\lim _{n\to \infty }a_{0}{\frac {1-q^{n+1}}{1-q}}={\frac {a_{0}}{1-q}},$

denn es ist $\lim _{n\to \infty }(1-q^{n+1})=1.$

Die letzte Formel ist sogar in jeder Banach-Algebra gültig, solange die Norm von $q$ kleiner als Eins ist; im Kontext linearer Operatoren spricht man auch von der Neumann-Reihe.

Herleitungen

Song von DorFuchs mit einer Herleitung der Gleichung für die geometrische Reihe

Herleitung der Formel für die Partialsummen

Die $n$-te Partialsumme der geometrischen Reihe lässt sich wie folgt berechnen:

$s_{n}=\sum _{k=0}^{n}a_{0}q^{k}=a_{0}+a_{0}q+a_{0}q^{2}+\dotsb +a_{0}q^{n}$

Vereinfacht:

$s_{n}=a_{0}(1+q+q^{2}+\dotsb +q^{n})$   (Gleichung 1)

Durch Multiplikation mit $q$ ergibt sich:

$qs_{n}=a_{0}(q+q^{2}+q^{3}+\dotsb +q^{n+1})$   (Gleichung 2)

Wenn man Gleichung 2 von Gleichung 1 subtrahiert, erhält man:

$s_{n}-qs_{n}=a_{0}(1-q^{n+1})$

Ausklammern von $s_{n}$:

$s_{n}(1-q)=a_{0}(1-q^{n+1})\$

Teilen durch $(1-q)$ liefert für $q\neq 1$ die gesuchte Formel für die Partialsummen:

$s_{n}=a_{0}{{1-q^{n+1}} \over {1-q}}$

Herleitung der Varianten

Mithilfe der oben angegebenen Formel lassen sich durch gliedweise Differentiation auch folgende endliche Reihen geschlossen darstellen, für $q\neq 1$

${\begin{aligned}\sum _{k=0}^{n}kq^{k}&=\sum _{k=0}^{n}q{\frac {\mathrm {d} }{\mathrm {d} q}}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{n}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1-q^{n+1}}{1-q}}\\&={\frac {nq^{n+2}-(n+1)q^{n+1}+q}{(1-q)^{2}}}\end{aligned}}$

${\begin{aligned}\sum _{k=0}^{n}k^{2}q^{k}&=\sum _{k=0}^{n}q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{n}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1-q^{n+1}}{1-q}}\\&={\frac {n^{2}q^{n+3}-(2n^{2}+2n-1)q^{n+2}+(n+1)^{2}q^{n+1}-q^{2}-q}{(q-1)^{3}}}\end{aligned}}$

Für $|q|<1$ konvergieren nach Grenzwertbildung der zugehörigen endlichen Reihe auch die unendlichen Reihen (folglich sind diese sogar gliedweise integrierbar):

$\sum _{k=0}^{\infty }kq^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{\infty }q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1}{1-q}}={\frac {q}{(1-q)^{2}}}$

$\sum _{k=0}^{\infty }k^{2}q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}\sum _{k=0}^{\infty }q^{k}=q{\frac {\mathrm {d} }{\mathrm {d} q}}q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {1}{1-q}}=q{\frac {\mathrm {d} }{\mathrm {d} q}}{\frac {q}{(1-q)^{2}}}={\frac {q(1+q)}{(1-q)^{3}}}$

analog für höhere Potenzen.

Mittels der Euler-Polynome $A_{s}(q)$ kann die Reihe auch für beliebige $s$ direkt angegeben werden.

$\sum _{k=0}^{\infty }k^{s}q^{n}={\frac {qA_{s}(q)}{(1-q)^{s+1}}}$

Allgemein stellt diese Variante die Definition des Polylogarithmus dar.

$\sum _{k=0}^{\infty }k^{s}q^{k}={\text{Li}}_{-s}(q)$

Quadratisches Analogon

Bei den Geometrischen Reihen nehmen die Folgenglieder bezüglich des Summenindex den Exponentiellen Verlauf an. Der vom Summenindex abhängige Exponent in den Folgegliedern hat bezüglich des Summenindex somit einen linearen Verlauf. Wenn aber der vom Summenindex abhängige Exponent in den Folgegliedern bezüglich des Summenindex stattdessen einen quadratischen Verlauf annimmt, und sich somit die Folgenglieder selbst bezüglich des Summenindex gleich dem Verlauf der Gaussschen Glockenkurve verhalten, dann sind die Werte der betroffenen unendlichen Summenreihen nicht elementar. Summen mit einem quadratischen Verlauf des Exponenten in den Folgengliedern bezüglich des Summenindex nehmen Elliptische Thetafunktionswerte an. Und diese Werte lassen sich sowohl mit den Jacobischen Thetafunktionen als auch mit den Nevilleschen Thetafunktionen darstellen. Diese Reihen haben generell folgenden Wert:

Ausdrucksform mit der Jacobischen Thetafunktion:

$\sum _{n=-\infty }^{\infty }x^{an^{2}+bn+c}=\exp {\bigl [}{\frac {1}{4a}}(4ac-b^{2})\ln(x){\bigr ]}{\bigl [}{\frac {-\pi }{a\ln(x)}}{\bigr ]}^{1/2}\vartheta _{00}{\biggl \{}{\frac {\pi b}{2a}};\exp {\bigl [}{\frac {\pi ^{2}}{a}}\ln(x)^{-1}{\bigr ]}{\biggr \}}$

Ausdrucksform mit der Nevilleschen Thetafunktion:

$\sum _{n=-\infty }^{\infty }x^{\,an^{2}+bn+c}=\exp {\bigl [}{\frac {1}{4a}}(4ac-b^{2})\ln(x){\bigr ]}\vartheta _{00}(x^{a})\,\theta _{d}{\biggl [}{\frac {b}{2}}\ln {\bigl (}{\frac {1}{x}}{\bigr )}\vartheta _{00}(x^{a})^{2};\psi _{H}(x^{a})^{4}{\biggr ]}$

Hierfür soll gelten: $(0<x<1)\,\,\cap \,\,(a,b,c\in \mathbb {R} ^{+})$

Die genannten Thetafunktionen sind nach Edmund Taylor Whittaker und George Neville WatsonThetafunktionen so definiert:

$\vartheta _{00}(v;w)=\prod _{n=1}^{\infty }(1-w^{2n})[1+2\cos(2v)w^{2n-1}+w^{4n-2}]$

$\theta _{d}(y;k)=\prod _{n=1}^{\infty }{\bigl [}1+q(k)^{2n-1}{\bigr ]}^{-2}{\bigl \{}1+2q(k)^{2n-1}\cos {\bigl [}2y\div {\bar {K}}(k){\bigr ]}+q(k)^{4n-2}{\bigr \}}$

Die Funktion $q(k)$ ist das Elliptische Nomen und die Funktion ${\bar {K}}(k)$ ist das reduzierte vollständige Elliptische Integral erster Art:

$q(k)=\exp {\bigl [}-\pi K({\sqrt {1-k^{2}}}\,)\div K(k){\bigr ]}$

${\bar {K}}(\varepsilon )={\frac {2}{\pi }}K(\varepsilon )$

$K(\varepsilon )=\int _{0}^{1}{\bigl [}(1-z^{2})(1-\varepsilon ^{2}z^{2}){\bigr ]}^{-1/2}\,\mathrm {d} z$

Das Kürzel $\vartheta _{00}$ stellt die sogenannte Theta-Nullwertfunktion dar und das Kürzel $\psi _{H}$ stellt die Hermitesche elliptische Psifunktion dar:

$\vartheta _{00}(w)=\prod _{n=1}^{\infty }(1-w^{2n})(1+w^{2n-1})^{2}$

$\psi _{H}(w)=\prod _{n=1}^{\infty }{\frac {1-w^{2n-1}}{1+w^{2n-1}}}$

Für die in diesem Abschnitt genannte Summenreihe werden die folgenden zwei Rechenbeispiele ausgeführt:

$\sum _{n=-\infty }^{\infty }{\bigl (}{\frac {7}{11}}{\bigr )}^{5n^{2}+3n+2}={\bigl (}{\frac {7}{11}}{\bigr )}^{31/20}{\bigl (}{\frac {\pi }{5}}{\bigr )}^{1/2}\ln {\bigl (}{\frac {11}{7}}{\bigr )}^{-1/2}\vartheta _{00}{\biggl \{}{\frac {3\pi }{10}};\exp {\bigl [}{\frac {1}{5}}\pi ^{2}\ln {\bigl (}{\frac {7}{11}}{\bigr )}^{-1}{\bigr ]}{\biggr \}}$

$\sum _{n=-\infty }^{\infty }{\bigl (}{\frac {7}{11}}{\bigr )}^{5n^{2}+3n+2}={\bigl (}{\frac {7}{11}}{\bigr )}^{31/20}\vartheta _{00}{\bigl [}{\bigl (}{\frac {7}{11}}{\bigr )}^{5}{\bigr ]}\theta _{d}{\biggl \{}{\frac {3}{2}}\ln {\bigl (}{\frac {11}{7}}{\bigr )}\vartheta _{00}{\bigl [}{\bigl (}{\frac {7}{11}}{\bigr )}^{5}{\bigr ]}^{2};\psi _{H}{\bigl [}{\bigl (}{\frac {7}{11}}{\bigr )}^{5}{\bigr ]}^{4}{\biggr \}}$

$\sum _{n=-\infty }^{\infty }{\bigl (}{\frac {23}{29}}{\bigr )}^{19n^{2}+17n+13}={\bigl (}{\frac {23}{29}}{\bigr )}^{699/76}{\bigl (}{\frac {\pi }{19}}{\bigr )}^{1/2}\ln {\bigl (}{\frac {29}{23}}{\bigr )}^{-1/2}\vartheta _{00}{\biggl \{}{\frac {17\pi }{38}};\exp {\bigl [}{\frac {1}{19}}\pi ^{2}\ln {\bigl (}{\frac {23}{29}}{\bigr )}^{-1}{\bigr ]}{\biggr \}}$

$\sum _{n=-\infty }^{\infty }{\bigl (}{\frac {23}{29}}{\bigr )}^{19n^{2}+17n+13}={\bigl (}{\frac {23}{29}}{\bigr )}^{699/76}\vartheta _{00}{\bigl [}{\bigl (}{\frac {23}{29}}{\bigr )}^{19}{\bigr ]}\theta _{d}{\biggl \{}{\frac {17}{2}}\ln {\bigl (}{\frac {29}{23}}{\bigr )}\vartheta _{00}{\bigl [}{\bigl (}{\frac {23}{29}}{\bigr )}^{19}{\bigr ]}^{2};\psi _{H}{\bigl [}{\bigl (}{\frac {23}{29}}{\bigr )}^{19}{\bigr ]}^{4}{\biggr \}}$

Die Nevilleschen Thetafunktionen selbst wurden vom Mathematiker Eric Harold Neville erforscht.

Siehe auch

• Die Konvergenz bzw. Divergenz der geometrischen Reihe ist die Grundlage für das Wurzelkriterium und das Quotientenkriterium.
• Geometrische Verteilung
• Arithmetische Reihe
• Harmonische Reihe

Literatur

• Albrecht Beutelspacher: Mathe-Basics zum Studienbeginn: Survival-Kit Mathematik. Springer, 2016, S. 198–199
• Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, 12. Aufl. 2015, ISBN 978-3-658-11544-9
• George E. Andrews: The Geometric Series in Calculus. The American Mathematical Monthly, Band 105, Nr. 1 (Jan., 1998), S. 36–40 (JSTOR:2589524)
• Joscelyn A. Jarrett: Regular Polygons and the Geometric Series. The Mathematics Teacher, Band 75, Nr. 3 (März 1982), S. 258–261 (JSTOR:27962874)

Weblinks

Commons: Geometric series – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Mathe für Nicht-Freaks: Geometrische Reihe – Lern- und Lehrmaterialien

Wikibooks: Mathe für Nicht-Freaks: Geometrische Summenformel – Lern- und Lehrmaterialien

• Eric W. Weisstein: Geometric Series. In: MathWorld (englisch).
• Geometrische Folgen und Reihen auf mathematische-basteleien.de
• Unendliche geometrische Reihe, Archivlink, abgerufen am 8. März 2022