Inkreis

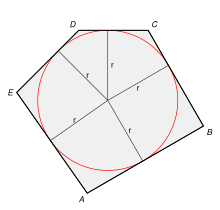
Der Inkreis eines Polygons (Vielecks) in der euklidischen Ebene ist der Kreis, der alle Seiten des Polygons in seinem Inneren berührt. Er berührt die Strecken zwischen den Eckpunkten und nicht ihre Verlängerungen. Gleichzeitig ist er der größte Kreis, der vollständig in dem gegebenen Polygon liegt.

Nur solche Polygone, bei denen sich alle Winkelhalbierenden der Innenwinkel des Polygons in einem Punkt schneiden, besitzen einen Inkreis. Der Schnittpunkt ist in diesem Fall der Mittelpunkt des Inkreises.

Existiert der Inkreis eines Polygons mit Flächeninhalt $A$ und Umfang $u$ , so hat der Inkreisradius den Wert

r={\frac {2A}{u}}

.

Inkreis eines Dreiecks

Eine besonders große Bedeutung hat der Inkreis in der Dreiecksgeometrie. Jedes Dreieck besitzt einen Inkreis, sein Mittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden. Zeichnet man um diesen Schnittpunkt einen Kreis, der eine Seite des Dreiecks berührt (die Seite wird somit eine Kreistangente des Inkreises), so berührt dieser Kreis auch die beiden anderen Seiten.

Alle Punkte der Winkelhalbierenden des Innenwinkels $\alpha =\angle BAC$ haben den gleichen Abstand von den Seiten $[AB]$ und $[CA]$ . Entsprechend haben die Punkte der Winkelhalbierenden von $\beta =\angle CBA$ den gleichen Abstand von $[BC]$ und $[AB]$ . Der Schnittpunkt dieser beiden Winkelhalbierenden hat also von allen drei Seiten des Dreiecks ( $[AB]$ , $[BC]$ und $[CA]$ ) gleichen Abstand. Er muss also auch auf der dritten Winkelhalbierenden liegen.

Der Inkreis berührt alle drei Seiten von innen – im Gegensatz zu den drei Ankreisen, die jeweils eine Seite von außen und die Verlängerungen der beiden anderen Seiten berühren.

Der Inkreismittelpunkt, also der Schnittpunkt der Winkelhalbierenden, zählt zu den ausgezeichneten Punkten des Dreiecks. Er trägt die Kimberling-Nummer $X_{1}$ .

Radius

Ist $A$ der Flächeninhalt des Dreiecks mit den Seiten $a$ , $b$ und $c$ , so berechnet sich der Radius $r$ des Inkreises durch

r={\frac {A}{s}}={\frac {2A}{a+b+c}}={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}}

mit

s={\frac {a+b+c}{2}}={\frac {u}{2}}

.

Dabei wurde für die Berechnung des Flächeninhalts $A$ des Dreiecks die Formel aus dem Satz des Heron verwendet.

Je nach den gegebenen Parametern des Dreiecks ist folgender Zusammenhang interessant:

r={\frac {a}{\cot \left({\frac {\beta }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)}}={\frac {b}{\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)}}={\frac {c}{\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\beta }{2}}\right)}}

Koordinaten

Die kartesischen Koordinaten des Inkreis-Mittelpunktes berechnen sich als das mit den Seitenlängen der gegenüberliegenden Seiten gewichtete Mittel der Eckpunkt-Koordinaten. Wenn sich die drei Eckpunkte bei $(x_{A}/y_{A})$ , $(x_{B}/y_{B})$ und $(x_{C}/y_{C})$ befinden, und die den Eckpunkten gegenüberliegenden Seiten die Längen $a$ , $b$ und $c$ haben, dann befindet sich der Inkreis-Mittelpunkt $I(x_{I}/y_{I})$ bei $\left({\frac {ax_{A}+bx_{B}+cx_{C}}{a+b+c}}/{\frac {ay_{A}+by_{B}+cy_{C}}{a+b+c}}\right)$ .

Baryzentrische Koordinaten: $(a:b:c)$

Trilineare Koordinaten: $(1:1:1)$

Weitere Eigenschaften

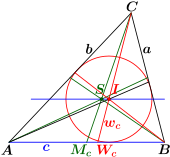
Die Entfernung zwischen der Ecke A und einem der benachbarten Berührpunkte des Inkreises ist gleich $s-a$ ; dabei bedeutet $s$ wie oben den halben Umfang. Entsprechendes gilt für die Ecken B und C.
Die Verbindungsgeraden der Ecken des Dreiecks mit den gegenüberliegenden Berührpunkten des Inkreises schneiden sich in einem Punkt, dem Gergonne-Punkt.
Der Satz vom Dreizack stellt einen Zusammenhang zwischen Umkreis und Inkreis her.
In jedem Dreieck ist das Produkt aus seinem Umfang und seinem Inkreisradius doppelt so groß wie seine Fläche (siehe Figur 1),^[1]^[2] was – wie in der Einleitung bereits festgestellt – für jedes Tangentenvieleck gilt.
Ist in einem nicht-gleichseitigen Dreieck die Grundseitenlänge das arithmetische Mittel der beiden übrigen Seitenlängen, so ist die Verbindungsgerade zwischen dem Schwerpunkt und dem Inkreismittelpunkt parallel zur Grundseite (Figur 2).

Beweis:

Aus

{\overline {AW_{c}}}+{\overline {W_{c}B}}={\frac {a+b}{2}}

(arithmetisches Mittel) und

{\overline {AW_{c}}}:{\overline {W_{c}B}}=b:a

(Winkelhalbierendensatz) folgt

{\overline {AW_{c}}}={\frac {b}{2}}

und

{\overline {W_{c}B}}={\frac {a}{2}}

.

Weil

AI

eine Winkelhalbierende im Teildreieck

AW_{c}C

ist, gilt hier nach dem Winkelhalbierendensatz

{\overline {CI}}:{\overline {IW_{c}}}=b:a=2:1

.

Da ferner

S

die Seitenhalbierende im Dreieck

ABC

ebenfalls im Verhältnis

2:1

teilt, gilt nach der Umkehrung des ersten Strahlensatzes

IS||AB

.^[3]

Inkreis eines rechtwinkligen Dreiecks

Liegt speziell ein rechtwinkliges Dreieck in der euklidischen Ebene vor, so lassen sich weitergehende Angaben zum Inkreis eines solchen Dreiecks machen.^[4]

Radius des Inkreises

Im Falle eines rechtwinkligen Dreiecks mit Seitenlängen $a$ , $b$ und $c$ , wobei $c$ die Länge der Hypotenuse sein soll, kann man für den Inkreisradius $r$ folgende Gleichungen angeben:

r={\frac {a\cdot b}{a+b+c}}={\frac {ab}{2s}}

r={\frac {a+b-c}{2}}=s-c

Der Beweis basiert auf den Eigenschaften des Inkreises im rechtwinkligen Dreieck. Mit Hilfe von Figur 3 ergibt sich

ab=r(a+b+c)

,

woraus unmittelbar die erste Behauptung folgt.

In Figur 4 lässt sich

c=(a-r)+(b-r)

ablesen. Durch einfache Umformung erhält man sofort die zweite Behauptung.^[5]

Flächenformel

Der Tangentialpunkt, in dem die Hypotenuse den Inkreis berührt, zerlegt diese in die Teilstrecken mit den Längen

x=s-a=b-r

und

y=s-b=a-r

.

Damit gilt dann für auf den Flächeninhalt $A$ des rechtwinkligen Dreiecks

A={\frac {a\cdot b}{2}}=(s-a)\cdot (s-b)=(a-r)\cdot (b-r)=x\cdot y

.

Inkreise anderer Vielecke

Während bei Dreiecken stets ein Inkreis existiert, trifft dies bei Vielecken (Polygonen) mit mehr als drei Ecken nur in Sonderfällen zu.

Vierecke, die einen Inkreis besitzen, heißen Tangentenvierecke. Zu ihnen gehören alle konvexen Drachenvierecke, insbesondere alle Rauten, also auch alle Quadrate.

Regelmäßige Polygone haben – unabhängig von der Zahl der Ecken – stets einen Inkreis. Für den Inkreisradius eines regelmäßigen $n$ -Ecks mit der Seitenlänge $a$ gilt:

r={\frac {a}{2}}\cot {\tfrac {180^{\circ }}{n}}={\frac {a}{2\tan {\frac {180^{\circ }}{n}}}}

Siehe auch

Literatur

Claudi Alsina, Roger B. Nelsen: Bezaubernde Beweise. Eine Reise durch die Eleganz der Mathematik. Springer Spektrum, Berlin (u. a.) 2013, ISBN 978-3-642-34792-4.
H. S. M. Coxeter, S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983, ISBN 3-12-983390-0.
Max Koecher, Aloys Krieg: Ebene Geometrie. 3., neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u. a. 2007, ISBN 978-3-540-49327-3.

Weblinks

Wiktionary: Inkreis – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Eric W. Weisstein: Incircle. In: MathWorld (englisch).
Walter Fendt: Inkreis eines Dreiecks wird Schritt für Schritt gezeichnet
Der Inkreis beim Dreieck. In: dwu-Unterrichtsmaterialien.de. Abgerufen am 13. Januar 2023.

Einzelnachweise

↑ Roger B. Nelsen: Beweise ohne Worte. Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin/Heidelberg, 2016, ISBN 978-3-662-50330-0, Seite 29.
↑ Grace Lin: Proof without Words: The Product of the Perimeter of a Triangle and Its Inradius Is Twice the Area of the Triangle. Mathematics Magazine, Band 72, Nr. 4 (Oktober 1999), S. 317 doi:10.2307/2691229.
↑ Eckard Specht, Erhard Quaisser, Patrick Bauermann (Hrsg.): 50 Jahre Bundeswettbewerb Mathematik - Die schönsten Aufgaben Zweite, erweiterte Auflage, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2020, ISBN 978-3-662-61165-4, S. 35–36
↑ Claudi Alsina, Roger B. Nelsen: Bezaubernde Beweise. Eine Reise durch die Eleganz der Mathematik. 2013, S. 89–90.
↑ Roger B. Nelsen: Beweise ohne Worte. Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin/Heidelberg, 2016, ISBN 978-3-662-50330-0, Seite 28.

[1] Roger B. Nelsen: Beweise ohne Worte. Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin/Heidelberg, 2016, ISBN 978-3-662-50330-0, Seite 29.

[2] Grace Lin: Proof without Words: The Product of the Perimeter of a Triangle and Its Inradius Is Twice the Area of the Triangle. Mathematics Magazine, Band 72, Nr. 4 (Oktober 1999), S. 317 doi:10.2307/2691229.

[3] Eckard Specht, Erhard Quaisser, Patrick Bauermann (Hrsg.): 50 Jahre Bundeswettbewerb Mathematik - Die schönsten Aufgaben Zweite, erweiterte Auflage, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2020, ISBN 978-3-662-61165-4, S. 35–36

[CA-RBN-I-4] Claudi Alsina, Roger B. Nelsen: Bezaubernde Beweise. Eine Reise durch die Eleganz der Mathematik. 2013, S. 89–90.

[5] Roger B. Nelsen: Beweise ohne Worte. Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin/Heidelberg, 2016, ISBN 978-3-662-50330-0, Seite 28.

[1]

[2]

[3]

[4]

[5]

Inkreis

Inhaltsverzeichnis