SL(2,R)

Die spezielle lineare Gruppe $\operatorname {SL} (2,\mathbb {R} )$ oder $\operatorname {SL} _{2}(\mathbb {R} )$ ist die Gruppe der reellen $2\times 2$-Matrizen mit Determinante 1:

${\mbox{SL}}(2,\mathbb {R} )=\left\{\left({\begin{matrix}a&b\\c&d\end{matrix}}\right):a,b,c,d\in \mathbb {R} {\mbox{ und }}ad-bc=1\right\}.$

Sie ist eine Lie-Gruppe mit vielfältigen Anwendungen in Geometrie, Topologie, Darstellungstheorie, harmonischer Analysis, Zahlentheorie, Modulformen und Physik.

Darstellungstheorie

Für jede natürliche Zahl $d$ gibt es eine, bis auf Isomorphismus eindeutige, $(d+1)$-dimensionale irreduzible Darstellung der $\operatorname {SL} (2,\mathbb {R} )$. Eine explizite Realisierung dieser irreduziblen Darstellung ist wie folgt. Sei

$V_{d}=\left\{f(x,y)=a_{0}x^{d}+a_{1}x^{d-1}y+a_{2}x^{d-2}y^{2}+\ldots +a_{d-1}xy^{d-1}+a_{d}y^{d}:a_{0},\ldots ,a_{d}\in \mathbb {R} \right\}$

der Vektorraum der homogenen Polynome vom Grad $d$ in 2 Variablen. Dieser Vektorraum ist $(d+1)$-dimensional und $A\in \operatorname {SL} (2,\mathbb {R} )$ wirkt durch

$(Af)(x,y):=f(A^{-1}(x,y)).$

Die Veronese-Einbettung $\nu _{d}\colon \mathbb {R} P^{1}\to \mathbb {R} P^{d}$ ist äquivariant bezüglich der irreduziblen Darstellung $\operatorname {SL} (2,\mathbb {R} )\to \operatorname {SL} (d+1,\mathbb {R} )$.

Die unendlich-dimensionalen Darstellungen der $\operatorname {SL} (2,\mathbb {R} )$ werden durch die Langlands-Klassifikation beschrieben.

Lie-Algebra

→ Hauptartikel: sl(2,R)

$\operatorname {SL} (2,\mathbb {R} )$ ist eine Lie-Gruppe, ihre Lie-Algebra ist die Lie-Algebra der spurfreien $2\times 2$-Matrizen

${\mathfrak {sl}}(2,\mathbb {R} )=\left\{A\in \operatorname {Mat} (2,\mathbb {R} ):\operatorname {Sp} (A)=0\right\}$.

Eine Vektorraum-Basis des 3-dimensionalen Vektorraumes ${\mathfrak {sl}}(2,\mathbb {R} )$ ist zum Beispiel

$H=\left({\begin{array}{cc}1&0\\0&-1\end{array}}\right),\ X=\left({\begin{array}{cc}0&1\\0&0\end{array}}\right),\ Y=\left({\begin{array}{cc}0&0\\1&0\end{array}}\right)$

mit den Kommutator-Relationen

$\left[H,X\right]=2X,\ \left[H,Y\right]=-2Y,\ \left[X,Y\right]=H$.

Diese Lie-Algebra ist einfach, sie hat zwei nicht-konjugierte Cartan-Unteralgebren: eine erzeugt von $H$, die andere von $X-Y$.

Die Killing-Form ist $B(V,W)=4\operatorname {Sp} (VW)$. Sie ist negativ definit auf dem von $X-Y$ erzeugten Unterraum, positiv definit auf dem von $H$ und $X+Y$ erzeugten Unterraum.

Lineare Algebra

Matrizen aus $\operatorname {SL} (2,\mathbb {R} )$ entsprechen invertierbaren linearen Abbildungen des Vektorraums $\mathbb {R} ^{2}$. Die Matrix $\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)$ wirkt durch

$\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)=\left({\begin{matrix}ax+by\\cx+dy\end{matrix}}\right).$

Matrizen aus $\operatorname {SL} (2,\mathbb {R} )$ erhalten die Volumenform, aber im Allgemeinen nicht die euklidische Metrik des $\mathbb {R} ^{2}$.

Klassifikation der 2×2-Matrizen

Die Eigenwerte einer Matrix $A\in \operatorname {SL} (2,\mathbb {R} )$ sind Nullstellen des charakteristischen Polynoms

$\lambda ^{2}-\mathrm {Sp} (A)\lambda +1=0$

und lassen sich nach der Lösungsformel für quadratische Gleichungen berechnen als

$\lambda ={\frac {\mathrm {Sp} (A)\pm {\sqrt {\mathrm {Sp} (A)^{2}-4}}}{2}}$.

Man klassifiziert die Matrizen dann entsprechend der folgenden Einteilung:

• Wenn $\vert \operatorname {Sp} (A)\vert <2$, dann ist $A$ eine elliptische Matrix.
• Wenn $\vert \operatorname {Sp} (A)\vert =2$, dann ist $A$ eine parabolische Matrix.
• Wenn $\vert \operatorname {Sp} (A)\vert >2$, dann ist $A$ eine hyperbolische Matrix.

Elliptische Elemente

Drehung mit Fixpunkt 0.

Elliptische Elemente sind von der Form

$A\left({\begin{matrix}\cos \phi &\sin \phi \\-\sin \phi &\cos \phi \end{matrix}}\right)A^{-1}$

mit $\phi \in \mathbb {R} /2\pi \mathbb {Z}$ und $A\in \operatorname {SL} (2,\mathbb {R} )$.

Die Matrix $\left({\begin{matrix}\cos \phi &\sin \phi \\-\sin \phi &\cos \phi \end{matrix}}\right)$ wirkt auf der euklidischen Ebene als Drehung mit Fixpunkt 0 und Drehwinkel $\phi$.

Parabolische Elemente

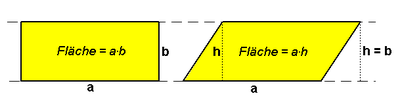
Eine Scherung bildet ein Rechteck auf ein Parallelogramm ab.

Parabolische Elemente sind von der Form

$\pm A\left({\begin{matrix}1&n\\0&1\end{matrix}}\right)A^{-1}$

mit $n\in \mathbb {R}$ und $A\in \operatorname {SL} (2,\mathbb {R} )$.

Die Matrix $\left({\begin{matrix}1&\ n\\0&1\end{matrix}}\right)$ wirkt auf der euklidischen Ebene als Scherung.

Hyperbolische Elemente

Das Bild-Parallelogramm hat denselben Flächeninhalt wie das ursprüngliche Quadrat.

Hyperbolische Elemente sind von der Form

$A\left({\begin{matrix}a&0\\0&{\frac {1}{a}}\end{matrix}}\right)A^{-1}$

mit $a\in \mathbb {R} \setminus \left\{0\right\}$ und $A\in \operatorname {SL} (2,\mathbb {R} )$.

Die Matrix $\left({\begin{matrix}a&0\\0&{\frac {1}{a}}\end{matrix}}\right)$ wirkt als Dehnstauchung, d. h., sie dehnt in Richtung eines Eigenvektors, staucht in Richtung des anderen Eigenvektors, erhält insgesamt aber den Flächeninhalt.

Hyperbolische Geometrie

Matrizen aus $\operatorname {SL} (2,\mathbb {R} )$ wirken auf der oberen Halbebene

$\mathbb {H} =\{x+iy\ |\ y>0;\,x,y\in \mathbb {R} \}\subset \mathbb {C}$

durch

$z\mapsto {\frac {az+b}{cz+d}}$.

Sie wirken als Isometrien der hyperbolischen Metrik.

Weil $\pm I_{2}$ als Identitätsabbildung wirkt, faktorisiert diese Wirkung von $\operatorname {SL} (2,\mathbb {R} )$ über

$\operatorname {PSL} (2,\mathbb {R} )=\operatorname {SL} (2,\mathbb {R} )/\{\pm I_{2}\}$.

Projektive Geometrie und gebrochen-lineare Transformationen

Die projektive Gerade $\mathbb {R} P^{1}$ ist die Menge aller Geraden durch den Nullpunkt im $\mathbb {R} ^{2}$. Die Wirkung von $\operatorname {SL} (2,\mathbb {R} )$ auf $\left(\mathbb {R} ^{2}\setminus \{0\}\right)$ gibt eine wohl-definierte Wirkung von $\operatorname {PSL} (2,\mathbb {R} )$ auf $\mathbb {R} P^{1}$.

Durch $[x:y]\rightarrow {\frac {x}{y}}$ wird eine Bijektion zwischen $\mathbb {R} P^{1}$ und $\mathbb {R} \cup \left\{\infty \right\}$ definiert. Nach dieser Identifizierung von $\mathbb {R} P^{1}$ und $\mathbb {R} \cup \left\{\infty \right\}$ wirkt $\operatorname {PSL} (2,\mathbb {R} )$ auf $\mathbb {R} \cup \left\{\infty \right\}$ durch gebrochen-lineare Transformationen

$\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)z={\frac {az+b}{cz+d}}$.

Die Veronese-Einbettung $\mathbb {R} P^{1}\to \mathbb {R} P^{n}$ ist äquivariant bzgl. der irreduziblen Darstellung $\operatorname {SL} (2,\mathbb {R} )\to \operatorname {SL} (n+1,\mathbb {R} )$.

$\mathbb {R} P^{1}=\mathbb {R} \cup \left\{\infty \right\}$ ist auch der Rand im Unendlichen $\partial \mathbb {H}$ der hyperbolischen Ebene $\mathbb {H}$. Die Wirkung von $PSL(2,\mathbb {R} )$ auf der Kompaktifizierung $\mathbb {H} \cup \partial \mathbb {H}$ der hyperbolischen Ebene durch gebrochen-lineare Transformationen ist stetig. Elliptische Elemente haben einen Fixpunkt in $\mathbb {H}$, parabolische Elemente haben einen Fixpunkt in $\partial \mathbb {H}$, hyperbolische Elemente haben zwei Fixpunkte in $\partial \mathbb {H}$.

Fuchssche Gruppen

Diskrete Untergruppen von $\operatorname {PSL} (2,\mathbb {R} )$ bezeichnet man als Fuchssche Gruppen.

Die Limesmenge einer Fuchsschen Gruppe $\Gamma$ ist der Durchschnitt von $\mathbb {R} P^{1}=\partial \mathbb {H}$ mit dem Abschluss einer Bahn $\Gamma x$, wobei und die Definition der Limesmenge unabhängig vom gewählten Punkt $x\in \mathbb {H}$ ist.

Eine Fuchssche Gruppe heißt Fuchssche Gruppe 1. Art, falls die Limesmenge ganz $\mathbb {P} ^{1}(\mathbb {R} )=\mathbb {R} \cup \{\infty \}$ ist. Andernfalls handelt es sich um eine Fuchssche Gruppe 2. Art.

Fuchssche Gruppen 1. Art sind die sogenannten Gitter in $\operatorname {PSL} (2,\mathbb {R} )$, d. h. diskrete Untergruppen $\Gamma$, für die es einen Fundamentalbereich endlichen Volumens in der hyperbolischen Ebene gibt.

Ein Beispiel eines Gitters in $\operatorname {SL} (2,\mathbb {R} )$ ist die modulare Gruppe $\operatorname {SL} (2,\mathbb {Z} )$, die unter anderem in der Theorie der Modulformen eine zentrale Rolle mit vielen zahlentheoretischen Anwendungen spielt.

Wenn eine Fuchssche Gruppe $\Gamma \subset \operatorname {PSL} (2,\mathbb {R} )$ keine Elemente der Ordnung 2 enthält, dann ist sie die Projektion einer diskreten Untergruppe von $\operatorname {SL} (2,\mathbb {R} )$. (Satz von Culler)

Topologie

Die Kreis-Gruppe $\operatorname {SO} (2)$ ist eine maximal kompakte Untergruppe von $\operatorname {SL} (2,\mathbb {R} )$. Die Untergruppe $\operatorname {SO} (2)$ ist ein Deformationsretrakt von $\operatorname {SL} (2,\mathbb {R} )$, insbesondere sind die beiden Räume homotopieäquivalent.

Die Fundamentalgruppe von $\operatorname {SL} (2,\mathbb {R} )$ ist isomorph zu $\mathbb {Z}$, die höheren Homotopiegruppen sind trivial.

Die universelle Überlagerung ${\widetilde {\operatorname {SL} (2,\mathbb {R} )}}$ von $\operatorname {SL} (2,\mathbb {R} )$ ist ein Beispiel einer Lie-Gruppe, welche keine treue endlich-dimensionale Darstellung besitzt, also zu keiner Untergruppe einer allgemeinen linearen Gruppe $\operatorname {GL} (n,\mathbb {R} )$ isomorph ist.

Der Quotient $\operatorname {PSL} (2,\mathbb {R} )=\operatorname {SL} (2,\mathbb {R} )/(\mathbb {Z} /2\mathbb {Z} )$ ist diffeomorph zum Einheitstangentialbündel der hyperbolischen Ebene: ${\operatorname {PSL} (2,\mathbb {R} )}=T^{1}\mathbb {H}$.

Literatur

• Serge Lang: SL₂(R) (= Graduate Texts in Mathematics. Bd. 105). Springer, New York NY u. a. 1985, ISBN 0-387-96198-4.
• William P. Thurston: Three-dimensional geometry and topology (= Princeton Mathematical Series. Bd. 35). Band 1. Edited by Silvio Levy. Princeton University Press, Princeton NJ, 1997, ISBN 0-691-08304-5.