Partielle Differentialgleichung

Eine partielle Differentialgleichung (Abkürzung PDG oder PDGL, beziehungsweise PDE für englisch partial differential equation) ist eine Differentialgleichung, die partielle Ableitungen enthält. Solche Gleichungen dienen der mathematischen Modellierung vieler physikalischer Vorgänge. Die Lösungstheorie von partiellen Differentialgleichungen ist für lineare Gleichungen weitgehend erforscht, bei nichtlinearen Gleichungen enthält die mathematische Theorie noch viele Lücken. Zur praktischen Berechnung von Lösungen werden in der Regel numerische Verfahren herangezogen.

Motivation und Beispiele

Darstellung einer zweidimensionalen Kugelwelle

Manche physikalische Prozesse lassen sich beschreiben, indem man die Veränderung einer Größe bezüglich einer einzelnen Variable betrachtet. So wird beispielsweise die Bewegung eines Massenpunktes im Raum durch die Bewegungsgleichung beschrieben, die nur Ableitungen nach der Zeit (nämlich Geschwindigkeit und Beschleunigung) enthält. Solche Gleichungen nennt man gewöhnliche Differentialgleichungen.

Viele andere physikalische Prozesse lassen sich aber nur dann beschreiben, wenn man die Veränderung einer Größe bezüglich mehrerer voneinander unabhängiger Variablen betrachtet. Fällt beispielsweise in regelmäßigen Abständen ein Wassertropfen auf eine Wasseroberfläche, so entsteht eine Kugelwelle, ähnlich wie im nebenstehenden Bild. Die entstehende Welle hängt sowohl von der Zeitableitung (Geschwindigkeit der Welle) als auch von der Raumableitung (Profil der Welle) ab. Da Ableitungen nach mehreren Variablen auftauchen, ist eine partielle Differentialgleichung zur Beschreibung des Vorgangs notwendig.

Darstellung der Lösung der eindimensionalen Transportgleichung bei gegebenen Anfangswerten

Eine sehr einfache partielle Differentialgleichung ist die lineare Transportgleichung in einer Raumdimension. Sie hat die Form

${\frac {\partial u(x,t)}{\partial t}}+c{\frac {\partial u(x,t)}{\partial x}}=0$

mit einem konstanten reellen Parameter $c$. Die gesuchte Funktion $u(x,t)$ ist von zwei Variablen abhängig, wobei üblicherweise $x$ den Ort und $t$ die Zeit bezeichnet. Nehmen wir an, dass die Funktion $u$ zu einer gewissen Zeit (etwa zu der Zeit $t=0$) bekannt ist. Es gelte also für alle $x$ im Definitionsbereich von $u$ eine Beziehung der Form $u(x,0)=g(x)$, wobei $g$ eine beliebig vorgegebene, mindestens einmal differenzierbare Funktion sei (Anfangsbedingung). Dann ist für beliebige Zeiten $t$ die Lösung der linearen Transportgleichung durch $u(x,t)=g(x-ct)$ gegeben. Diese Gleichung bedeutet nichts anderes, als dass die Anfangsdaten $g$ in unveränderter Form mit der Geschwindigkeit $c$ in Richtung der positiven x-Achse verschoben („transportiert“) werden (längs der Charakteristik der Gleichung), siehe nebenstehendes Bild. Ein Anwendungsbeispiel wäre der Transport eines im Wasser gelösten Stoffes mit der Strömung des Wassers, also zum Beispiel der Transport von Schadstoffen in einem Fluss (wobei die Diffusion des Stoffes vernachlässigt wird).

Weitere Beispiele partieller Differentialgleichungen sind die Poisson-Gleichung bzw. die Laplace-Gleichung, die Wärmeleitungsgleichung, die Wellengleichung und Burgersgleichung. Für die Anwendungen von großer Bedeutung sind die Euler- bzw. die Navier-Stokes-Gleichungen, die Maxwell-Gleichungen, die Gleichungen der Magnetohydrodynamik, die Schrödingergleichung und die Korteweg-de-Vries-Gleichung.

Definition

Eine partielle Differentialgleichung ist eine Gleichung (oder ein Gleichungssystem) für eine oder mehrere unbekannte Funktionen, die folgende Kriterien erfüllt:

• die unbekannte Funktion hängt von mindestens zwei Variablen ab (wenn sie nur von einer Variable abhängt, bezeichnet man sie als gewöhnliche Differentialgleichung, oder kurz nur Differentialgleichung)
• in der Gleichung kommen partielle Ableitungen nach mindestens 2 Variablen vor
• in der Gleichung kommen nur die Funktion sowie deren partielle Ableitungen, jeweils am gleichen Punkt ausgewertet, vor.

Die implizite Form einer partiellen Differentialgleichung für eine Funktion $u$, die von zwei Variablen $x$ und $y$ abhängt, lautet

$F\left(x,y,u(x,y),{\frac {\partial u(x,y)}{\partial x}},{\frac {\partial u(x,y)}{\partial y}},\ldots ,{\frac {\partial ^{2}u(x,y)}{\partial x\partial y}},\ldots \right)=0,$

wobei $F$ eine beliebige Funktion ist. Im mehrdimensionalen Fall schreibt man auch

$F\left(x,u(x),\operatorname {D} u,\operatorname {D} ^{2}u,\ldots \operatorname {D} ^{k}u,\ldots \right)=0$

mit den partiellen Ableitungen $D^{k}u$ vom Grad $k$.

Gleichungen, in denen neben partiellen Ableitungen auch Integrale auftreten, nennt man Integro-Differentialgleichungen.

Einteilung

Partielle Differentialgleichungen können nach verschiedenen Kriterien eingeteilt werden. Das Lösungsverhalten und damit die theoretische und numerische Behandlung der so eingeteilten Gleichungen unterscheiden sich je nach verwendetem Kriterium erheblich voneinander.

Anzahl der Ableitungen

Den Grad der höchsten Ableitung, der in der Gleichung vorkommt, nennt man die Ordnung. Beispielsweise treten in einer Gleichung erster Ordnung nur partielle erste Ableitungen auf. Im Allgemeinen sind Gleichungen höherer Ordnung schwieriger zu lösen als Gleichungen niedrigerer Ordnung.

Anzahl der Variablen

Bei vielen partiellen Differentialgleichungen spielt die Anzahl der Variablen eine Rolle bei den Möglichkeiten der theoretischen Untersuchung und der numerischen Lösung. So konnten etwa im Fall der Navier-Stokes-Gleichungen in zwei Raumdimensionen weitreichende Existenz-, Eindeutigkeits- und Regularitätsaussagen bewiesen werden, während die Frage nach Existenz und Eindeutigkeit glatter Lösungen im dreidimensionalen Fall offen ist. Dieses Problem wurde in die Liste der Millennium-Probleme aufgenommen.

Lineare und nichtlineare Gleichungen

Man spricht von einer linearen partiellen Differentialgleichung, falls die unbekannte Funktion sowie alle auftretenden Ableitungen linear vorkommen. Dies bedeutet, dass die Koeffizientenfunktionen vor der unbekannten Funktion bzw. ihrer Ableitungen nur von den Veränderlichen abhängen (und nicht von der Funktion selbst). Eine lineare partielle Differentialgleichung 2. Ordnung in zwei Variablen hat also die folgende allgemeine Form:

$a(x,y){\frac {\partial ^{2}u(x,y)}{\partial x^{2}}}+b(x,y){\frac {\partial ^{2}u(x,y)}{\partial x\partial y}}+c(x,y){\frac {\partial ^{2}u(x,y)}{\partial y^{2}}}+d(x,y){\frac {\partial u(x,y)}{\partial x}}+e(x,y){\frac {\partial u(x,y)}{\partial y}}+f(x,y)u(x,y)=g(x,y)$.

Man spricht von einer semilinearen Gleichung, falls alle Ableitungen von höchster Ordnung linear auftreten, dies aber nicht mehr für die Funktion und Ableitungen niedriger Ordnung gilt.

Man spricht von einer quasilinearen partiellen Differentialgleichung, falls die Koeffizientenfunktionen vor der höchsten Ableitung zusätzlich von niedrigeren Ableitungen und der unbekannten Funktion abhängen.

In allen anderen Fällen spricht man von einer nichtlinearen partiellen Differentialgleichung. Nichtlineare partielle Differentialgleichungen kann man durch Ausdifferenzieren immer in eine quasilineare Form überführen. Nichtlineare Gleichungen beschreiben in aller Regel weitaus komplexere Phänomene als lineare Gleichungen, wie beispielsweise turbulente Strömungen (im Vergleich zu Kriechströmungen). Nichtlineare Probleme sind sowohl aus theoretischer wie auch aus numerischer Sicht schwieriger zu behandeln als lineare Probleme. Ein einfaches Beispiel einer nichtlinearen partiellen Differentialgleichung ist die Burgersgleichung:

${\frac {\partial u(x,t)}{\partial t}}+u(x,t){\frac {\partial u(x,t)}{\partial x}}=0$.

Da ihre Lösungen vollständig bekannt sind, dient sie häufig als Modellproblem für allgemeinere nichtlineare Gleichungen, wie etwa der Euler-Gleichungen.

Einteilung nach Grundtypus

Häufig werden partielle Differentialgleichungen einem der drei Grundtypen elliptisch, parabolisch oder hyperbolisch zugeordnet. Diese Klassifikation ist nicht erschöpfend; es kann also nicht jede Gleichung einem dieser Typen zugeordnet werden. Sie ist aber sinnvoll, da sehr viele in der Praxis auftretenden Gleichungen in dieses Schema fallen und die drei Grundtypen fundamental unterschiedliche Eigenschaften besitzen. Die Klassifikation wird zunächst für den wichtigen Fall einer einzelnen Gleichung 2. Ordnung beschrieben. Beispiele und Eigenschaften der Grundtypen werden im Abschnitt Grundtypen partieller Differentialgleichungen erläutert.

Gleichungen 2. Ordnung

Zwei Variablen

Als Beispiel für die Einteilung in die drei Grundtypen elliptische, parabolische und hyperbolische Differentialgleichungen betrachten wir die allgemeine lineare partielle Differentialgleichung 2. Ordnung mit zwei Variablen

$a(x,y){\frac {\partial ^{2}u(x,y)}{\partial x^{2}}}+b(x,y){\frac {\partial ^{2}u(x,y)}{\partial x\partial y}}+c(x,y){\frac {\partial ^{2}u(x,y)}{\partial y^{2}}}+d(x,y){\frac {\partial u(x,y)}{\partial x}}+e(x,y){\frac {\partial u(x,y)}{\partial y}}+f(x,y)u(x,y)=0$

und definieren $D(x,y):=a(x,y)c(x,y)-\left({\tfrac {b(x,y)}{2}}\right)^{2}$. Gilt nun

• $D(x,y)>0$, so heißt die Gleichung elliptisch im Punkt $(x,y)$,
• $D(x,y)=0$, so heißt die Gleichung parabolisch im Punkt $(x,y)$,
• $D(x,y)<0$, so heißt die Gleichung hyperbolisch im Punkt $(x,y)$.

Bei dieser Klassifizierung werden nur die Koeffizientenfunktionen der höchsten Ableitungen betrachtet. Da die Koeffizientenfunktionen $a$, $b$, $c$ von $x$ und $y$ abhängen, hängt der Typ der Differentialgleichung vom Ort ab.

Mit der obigen Definition ergibt sich die Elliptizität der Poisson-Gleichung, die Parabolizität der Wärmeleitungsgleichung und die Hyperbolizität der Wellengleichung. Die genannten drei Gleichungen stellen jeweils den sogenannten Normaltyp aller Gleichungen ihres Grundtyps dar.

Der Ursprung der Bezeichnungen elliptisch, parabolisch und hyperbolisch ergibt sich aus der Theorie der Kegelschnitte. Die allgemeine Kegelschnittgleichung

$ax^{2}+2bxy+cy^{2}+2dx+2ey+f\,=\,0$

ist von der Struktur her ähnlich aufgebaut wie die oben angegebene lineare partielle Differentialgleichung 2. Ordnung. Für die Koeffizienten $a$, $b$, $c$ gelten analoge Bedingungen wie oben, damit aus den entsprechenden Kegelschnitten eine Ellipse, Parabel oder Hyperbel entsteht.

Die oben definierte Einteilung in elliptisch, parabolisch und hyperbolisch kann man auch durch die Betrachtung der Definitheit der Koeffizientenmatrix

$A(x,y):={\begin{pmatrix}a(x,y)&{\frac {b(x,y)}{2}}\\{\frac {b(x,y)}{2}}&c(x,y)\end{pmatrix}}$

erhalten. Ist

• $A(x,y)$ positiv definit oder negativ definit, so heißt die Gleichung elliptisch im Punkt $(x,y)$,
• $A(x,y)$ positiv semidefinit oder negativ semidefinit, aber nicht definit (singulär), so heißt die Gleichung parabolisch im Punkt $(x,y)$,
• $A(x,y)$ indefinit (mit genau einem negativen Eigenwert), so heißt die Gleichung hyperbolisch im Punkt $(x,y)$.

Eine lineare Gleichung zweiter Ordnung in zwei Unbekannten mit reellen, konstanten Koeffizienten lässt sich genau einem dieser Typen zuordnen. Sobald die Koeffizienten nicht konstant bezüglich $(x,y)$ sind oder die Gleichung nichtlinear ist, gibt es auch Gleichungen die sich nicht nach diesem Schema klassifizieren lassen. Gleiches gilt für die unten beschriebenen Allgemeineren Fälle.

n Variablen

Die Typeinteilung anhand der Koeffizientenmatrix lässt sich auch auf Gleichungen der Ordnung 2 mit mehr als zwei Variablen übertragen. In diesem Fall erstellt man anhand der Differentialgleichung eine Matrix $A({\vec {x}})$ mit den Koeffizientenfunktionen der partiellen Ableitungen zweiter Ordnung als Einträgen. In Verallgemeinerung des obigen Falls gilt: Ist

• $A({\vec {x}})$ positiv definit oder negativ definit, so heißt die Gleichung elliptisch im Punkt ${\vec {x}}$,
• $A({\vec {x}})$ semidefinit mit Null als einfachem Eigenwert, so heißt die Gleichung parabolisch im Punkt ${\vec {x}}$,
• $A({\vec {x}})$ indefinit mit von Null verschiedenen Eigenwerten, so heißt die Gleichung hyperbolisch im Punkt ${\vec {x}}$.

Rand- und Anfangswertprobleme

Die Lösung einer partiellen Differentialgleichung ist im Allgemeinen nicht eindeutig bestimmt. Um eine eindeutige Lösung zu erhalten, bedarf es gewisser Zusatzbedingungen, sogenannter Anfangs- und/oder Randbedingungen. Im Gegensatz zu der Situation bei gewöhnlichen Differentialgleichungen führt aber nur eine dem jeweiligen Grundtyp angepasste Wahl der Anfangs- und Randbedingungen zu einem korrekt gestellten Problem. Typische Beispiele korrekt gestellter Probleme sind:

• Dirichlet-Randbedingungen für elliptische Probleme
• Neumann-Randbedingungen für elliptische Probleme
• schiefe Randbedingungen (auch: Robin-Randbedingungen) für elliptische Probleme
• Anfangs- und Randbedingungen für parabolische Probleme
• Anfangsbedingungen für hyperbolische Probleme

Theorie

Methoden der Funktionalanalysis

Während bei gewöhnlichen Differentialgleichungen das Problem der Existenz und der Eindeutigkeit der Lösung durch den Satz von Picard-Lindelöf in sehr befriedigender Weise gelöst ist, existiert bei partiellen Differentialgleichungen keine derart weitreichende allgemeine Lösungstheorie. Zwar garantiert der Satz von Cauchy-Kowalewskaja die lokale Existenz und Eindeutigkeit der Lösung partieller Differentialgleichungen mit analytischen Koeffizientenfunktionen, aber dieses Resultat lässt sich nicht auf allgemeinere Koeffizientenfunktionen ausdehnen. Bereits für beliebig oft differenzierbare, nichtanalytische Koeffizientenfunktionen gibt es ein Gegenbeispiel (Beispiel von Lewy).

Da eine befriedigende einheitliche Theorie zu partiellen Differentialgleichungen nicht existiert, teilt man diese je nach Lösungsverhalten in verschiedene Typen ein. Die verschiedenen Typen werden mit jeweils unterschiedlichen Techniken analysiert, um Aussagen über Existenz, Eindeutigkeit und weitere Eigenschaften der Lösungen zu erhalten. Lineare partielle Differentialgleichungen sind auch im Fall mehrdimensionaler Systeme hinreichend gut untersucht. Für nichtlineare partielle Differentialgleichungen gilt das nicht.

Bei der theoretischen Untersuchung der Lösungen von partiellen Differentialgleichungen stößt man, solange man nur nach sogenannten klassischen (d.h. hinreichend oft differenzierbaren) Lösungen sucht, sehr schnell auf große Schwierigkeiten in der mathematischen Theorie. Zudem ist in manchen Fällen (zum Beispiel bei der Beschreibung von Stoßwellen) aus physikalischen Gründen gar nicht mit der Existenz von stetigen oder differenzierbaren Lösungen zu rechnen. Aus diesen Gründen sind in der sogenannten klassischen Theorie in vielen Fällen keine oder keine hinreichend guten Existenz- und Eindeutigkeitsaussagen möglich. Als Ausweg schwächt man den Begriff der "Lösung einer Differentialgleichung" in geeigneter Weise ab, d.h. man erlaubt auch Lösungen, die (im klassischen Sinne) nicht differenzierbar sind. Mit diesen erweiterten Lösungsbegriffen sind nun in der sogenannten schwachen Theorie hinreichend gute theoretische Aussagen möglich. Weiterhin bildet dieser abgeschwächte Lösungsbegriff die Grundlage vieler numerischer Verfahren zur approximativen Lösung von partiellen Differentialgleichungen.

Bei der Untersuchung von partiellen Differentialgleichungen treten also verschiedene Lösungsbegriffe auf:

• klassische Lösung: Die Lösung ist hinreichend oft stetig differenzierbar und die Gleichung wird durch Einsetzen dieser Ableitungen in jedem Punkt des zu Grunde liegenden Gebiets erfüllt.
• starke Lösung: Die Lösung ist im Sinne der schwachen Ableitung hinreichend oft differenzierbar und die Gleichung wird durch Einsetzen der schwachen Ableitungen fast überall erfüllt.
• schwache Lösung: Hierbei wird die Gleichung mit Testfunktionen multipliziert, integriert und dann zumindest teilweise partiell integriert. Eine Funktion aus einem geeigneten Funktionenraum (meist einem Sobolev-Raum), die diese neue Gleichung für alle Testfunktionen erfüllt, nennt man schwache Lösung.
• milde Lösung: Starke Lösungen erfüllen häufig eine Form der Variation der Konstanten-Formel. Eine Lösung dieser Formel nennt man milde Lösung. Eine milde Lösung muss jedoch keine starke Lösung sein.
• maßwertige Lösung: für gewisse Klassen von Gleichungen ist ein maßtheorietischer Lösungsbegriff sinnvoll, um auch mögliche Konzentrationseffekte beschreiben zu können.
• distributionelle Lösung: Die Lösung ist eine Distribution und erfüllt die Gleichung im Sinne der Distributionentheorie. Alle Ableitungen werden auf die als beliebig glatt angenommenen Testfunktionen „umgewälzt“. Da nichtlineare Operationen auf Distributionen im Allgemeinen nicht definiert sind, ist dieser Lösungsbegriff nur für lineare Gleichungen sinnvoll.

Diese Begriffe werden in der Literatur nicht einheitlich verwendet, sodass immer auf die jeweilige Definition Bezug genommen werden muss.

Mit Hilfe der sogenannten Regularitätstheorie und den Sobolewschen Einbettungssätzen kann man unter geeigneten Voraussetzungen an die Differentialgleichung oftmals zeigen, dass die erhaltene distributionelle oder schwache Lösung auch eine starke oder sogar klassische Lösung ist.

Lie-Theorie

→ Hauptartikel: Lie-Theorie

Ein strukturierter allgemeiner Ansatz zur Lösung von Differentialgleichungen wird über die Symmetrie und die kontinuierliche Gruppentheorie verfolgt. 1870 stellte Sophus Lie in seiner Arbeit die Theorie der Differentialgleichungen mit der Lie-Theorie auf eine allgemeingültige Grundlage. Er zeigte, dass die älteren mathematischen Theorien zur Lösung von Differentialgleichungen durch die Einführung von sogenannten Lie-Gruppen zusammengefasst werden können. Ein allgemeiner Ansatz zur Lösung von Differentialgleichungen nutzt die Symmetrie-Eigenschaft der Differentialgleichungen aus. Dabei werden kontinuierliche infinitesimale Transformationen angewendet, die Lösungen auf (andere) Lösungen der Differentialgleichung abbilden. Kontinuierliche Gruppentheorie, Lie-Algebren und Differentialgeometrie werden verwendet, um die tiefere Struktur der linearen und nichtlinearen (partiellen) Differentialgleichungen zu erfassen und die Zusammenhänge abzubilden, siehe dazu auch die Themen Lax-Paare, Rekursive Operatoren, Kontakt- und Bäcklund-Transformationen, die schließlich zu den exakten analytischen Lösungen einer Differentialgleichung führen. Symmetrie-Methoden werden benutzt, um Differentialgleichungen exakt zu lösen.

Grundtypen

Zur Einteilung siehe Abschnitt Einteilung nach Grundtypus.

Elliptische partielle Differentialgleichungen

→ Hauptartikel: Elliptische partielle Differentialgleichung

Lösung der Laplace-Gleichung auf einem Kreisring mit den Dirichlet-Randwerten u(r=2)=0 und u(r=4)=4sin(5*θ)

Elliptische partielle Differentialgleichungen treten typischerweise im Zusammenhang mit zeitunabhängigen (stationären) Problemen auf. Ein Kennzeichen ist, dass elliptische Gleichungen oftmals einen Zustand minimaler Energie beschreiben, also aus dem Variationsproblem einer nach unten beschränkten Wirkung herrühren. Die bekanntesten Beispiele sind die Laplace-Gleichung und die Poisson-Gleichung. Diese Gleichungen beschreiben etwa die (stationäre) Temperaturverteilung in einem Körper oder auch die elektrostatische Ladungsverteilung in einem Körper. Außerdem ist das (newtonsche) Gravitationspotential eine Lösung der Poisson-Gleichung.

Bei elliptischen Gleichungen sind die am häufigsten auftretenden Randbedingungen entweder Dirichlet-Randbedingungen oder Neumann-Randbedingungen. Die erste bedeutet, dass die Werte der gesuchten Funktion auf dem Rand vorgegeben sind, während die zweite eine Vorgabe der Normalenableitung der gesuchten Funktion ist. Am Beispiel der Temperaturverteilung soll der Unterschied gezeigt werden: Steckt man ein Objekt in Eiswasser, dann beträgt die Temperatur am Rand 0 Grad Celsius. Damit ist die Temperaturverteilung im Inneren die Lösung eines Dirichlet-Randwertproblems. Ein anderer Fall tritt auf, wenn man den Körper isoliert. Hier ist zwar die Temperatur unbekannt, aber aufgrund der Isolation beträgt der Wärmefluss am Rand 0. Da der Fluss mit der Normalenableitung in Verbindung gebracht werden kann, führt dies auf ein Neumann-Problem. Ähnliches gilt in der Elektrostatik: Kennt man die Spannung, die am Rand angelegt wird, kommt man zu einem Dirichlet-Problem, kennt man hingegen die Stromstärke am Rand, erhält man ein Neumann-Problem.

Eine nichtlineare elliptische Gleichung ist die Gleichung für Minimalflächen (Minimal surface equation), die die Form einer Seifenhaut beschreibt, die sich beim Eintauchen eines Drahtgestells in Seifenlauge bildet.

Parabolische partielle Differentialgleichungen

Lösung einer zweidimensionalen Wärmeleitungsgleichung

→ Hauptartikel: Parabolische partielle Differentialgleichung

Dieser Typ von Gleichungen beschreibt ähnliche Phänomene wie elliptische Gleichungen, aber im instationären Fall. Das bei weitem wichtigste Beispiel einer parabolischen Gleichung ist die Wärmeleitungsgleichung, die das Abkühlen und Aufheizen eines Körpers beschreibt. Diffusionsprozesse werden ebenfalls durch diese Gleichung beschrieben. Parabolische Gleichungen führen auf ein Anfangs-Randwertproblem. Beispielsweise müssen bei der Wärmeleitungsgleichung am (räumlichen) Rand des Gebietes für alle Zeiten entweder die Temperatur oder der Temperaturfluss vorgegeben werden. Dies entspricht dem Fall von Dirichlet- oder Neumannbedingungen im elliptischen Fall. Zusätzlich muss die Temperaturverteilung am Anfang, also zum Zeitpunkt $t=0$ vorgegeben werden. Insgesamt benötigen also parabolische Gleichungen räumliche Randbedingungen und zeitliche Anfangswerte. Ein weiteres, nichtlineares Beispiel einer parabolischen Gleichung ist die Korteweg-de-Vries-Gleichung, die Wasserwellen in Ufernähe beschreibt.

Hyperbolische partielle Differentialgleichungen

Schwingende Membran als Lösung einer zweidimensionalen Wellengleichung

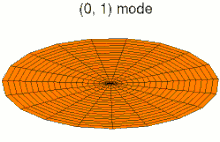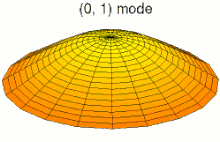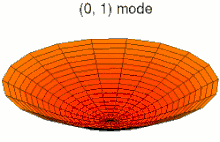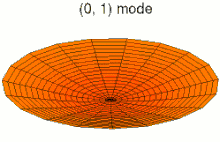
Die typische hyperbolische Gleichung ist die Wellengleichung. Allgemein werden durch diese Art von Gleichungen Wellen und deren Ausbreitung beschrieben. Außerdem sind einzelne Gleichungen erster Ordnung immer hyperbolisch (im Gegensatz zu Systemen erster Ordnung, wo wieder verschiedene Fälle möglich sind). Im Unterschied zu parabolischen und elliptischen Gleichungen werden Lösungen hyperbolischer Gleichungen wenig bis gar nicht gedämpft. Das führt einerseits zu einer komplizierten Lösungstheorie, da mit weniger Differenzierbarkeit gerechnet werden kann. Andererseits können sich Wellen erst durch diese fehlende Dämpfung über weite Strecken ausbreiten.

Die zu diesem Typ gehörigen Anfangs- und Randwerte führen auf Cauchy-Probleme. Das bedeutet, dass wie im parabolischen Fall zusätzlich zu räumlichen Randbedingungen Anfangswerte benötigt werden. Zur Lösung hyperbolischer Gleichungen zweiter Ordnung benötigt man aber zwei Anfangswerte – den Funktionswert und die zeitliche Ableitung desselben am Anfang. Am Beispiel einer eingespannten Saite soll dies verdeutlicht werden: Die Auslenkung der Saite erfüllt die Wellengleichung. Wenn die Saite an den Enden eingespannt ist, führt dies auf die räumlichen Randbedingungen, in diesem Fall ist die Auslenkung am Rand 0 (weil eingespannt), damit ist der Funktionswert am Rand bekannt und es ergeben sich Dirichlet-Randbedingungen. (Im Fall von frei schwingenden Objekten, wie der Luftsäule in Holzblasinstrumenten, kommt man dementsprechend auf Neumann-Randbedingungen.) Zusätzlich müssen jetzt noch zwei Anfangsbedingungen vorgegeben werden: Die Auslenkung am Anfang (entspricht dem Funktionswert), und die Geschwindigkeit, mit der die Saite am Anfang angezupft wird (entspricht der zeitlichen Ableitung). Mit diesen Bedingungen kann die Auslenkung zu allen späteren Zeitpunkten eindeutig angegeben werden.

Hyperbolische Gleichungen mit paarweise verschiedenen Eigenwerten heißen strikt hyperbolisch. Hier ist die Lösungstheorie auch für nichtlineare Systeme bekannt. Sind die Gleichungen nicht strikt hyperbolisch, wie beispielsweise die mehrdimensionalen Euler-Gleichungen oder die Gleichungen der Magnetohydrodynamik, ist dies nicht mehr der Fall.

Numerische Verfahren

Die meistbenutzten numerischen Verfahren sind die Methode der finiten Elemente (FEM), der finiten Differenzen (FDM) und der finiten Volumina (FVM). In den letzten Jahren wird auch verstärkt die Randelement-Methode (REM oder engl. BEM) benutzt.

All diese Verfahren basieren auf einer Diskretisierung der partiellen Differentialgleichung, bei der die Lösung mit Hilfe eines endlichdimensionalen Gebildes approximiert wird.

Literatur

Historische Literatur

• Heinrich Weber: Die partiellen Differential-Gleichungen der mathematischen Physik nach Riemann’s Vorlesungen, Braunschweig: F. Vieweg und sohn, 1900–01.
• Jakob Horn: Einführung in die Theorie der partiellen Differentialgleichungen, Leipzig: G. J. Göschen, 1910.
• Richard Courant und David Hilbert: Methoden der Mathematischen Physik, Zweiter Band, Berlin: J. Springer, 1937.
• Olga Alexandrowna Ladyschenskaja, Nina Nikolajewna Uralzewa: Linear and Quasilinear Equations of Elliptic Type. Übersetzt durch L. Ehrenpreis, Academic Press, New York/London 1968, ISBN 0124328504.
• Olga Alexandrowna Ladyschenskaja, W. A. Solonnikow, Nina N. Uralzewa: Linear and Quasi-linear Equations of Parabolic Type. Übersetzt durch S. Smith, American Mathematical Society, Providence, Rhode Island, 1968, ISBN 0821815733.

Moderne Literatur

• David Gilbarg, Neil Trudinger: Elliptic Partial Differential Equations of Second Order. In: Grundlehren der mathematischen Wissenschaften. Band 224, Springer-Verlag, Berlin/Heidelberg/New York 1977, ISBN 3-540-08007-4.
• Lawrence Craig Evans: Partial Differential Equations. In: Graduate Studies in Mathematics. Band 19, American Mathematical Society, Providence, Rhode Island, 1999, ISBN 0-8218-0772-2.
• Gerhard Dziuk: Theorie und Numerik partieller Differentialgleichungen. de Gruyter, Berlin 2010, ISBN 978-3-11-014843-5.
• Fritz John: Partial Differential Equations, 4. Auflage, Springer Verlag 1982, 1991, ISBN 0387906096
• Jürgen Jost: Partielle Differentialgleichungen. Springer, Berlin, 1998, ISBN 3-540-64222-6.
• Randall J. LeVeque: Finite volume methods for hyperbolic problems. Cambridge Univ. Press, Cambridge 2002, ISBN 0-521-00924-3.
• T. Roubíček: Nonlinear Partial Differential Equations with Applications. Birkhäuser, Basel, 2nd Ed.: 2013, ISBN 978-3-0348-0512-4 (DOI: 10.1007/978-3-0348-0513-1).
• B. Schweizer: Partielle Differentialgleichungen. Springer, Heidelberg 2013, ISBN 978-3-642-40637-9.

Literatur zur Lie-Theorie

• Nail H. Ibragimov CRC Handbook of Lie Group Analysis of Differential Equations Vol. 1-3CRC-Press 1993 ISBN 0849344883.
• Hans Stephani Differential Equations: Their Solution Using Symmetries. Edited by M. MacCallum, Cambridge University Press 1989.
• Peter Olver 1995 Equivalence, Invariants and Symmetry Cambridge Press 1995