„Spannungstensor“ – Versionsunterschied
| [gesichtete Version] | [gesichtete Version] |
K HC: Entferne Kategorie:Festigkeitslehre; Ergänze Kategorie:Mechanische Spannung |
Impulsbilanz, maximale Schubspannung, Zugversuch, GND |
||
| Zeile 1: | Zeile 1: | ||
{{Dieser Artikel|beschreibt den Spannungstensor der |
{{Dieser Artikel|beschreibt den Spannungstensor der Kontinuumsmechanik. Für den Maxwellschen Spannungstensor siehe [[Energie-Impuls-Tensor]].}} |
||
Ein '''Spannungstensor''' ist ein [[Tensor]] zweiter Stufe, der die [[Spannung (Mechanik)|mechanischen Spannungen]] an einem bestimmten Punkt innerhalb der Materie beschreibt. Er ist eine wesentliche |
Ein '''Spannungstensor''' ist ein [[Tensor]] zweiter Stufe, der die [[Spannung (Mechanik)|mechanischen Spannungen]] an einem bestimmten Punkt innerhalb der Materie beschreibt. Er ist eine wesentliche Größe der [[Kontinuumsmechanik]], in der er bei der Formulierung [[Physikalisches Gesetz|physikalischer Gesetze]] auftritt. Die Beschleunigung der Materieelemente wird durch die ''[[Divergenz eines Vektorfeldes|räumliche Änderung]]'' des Spannungstensors bewirkt – ggf. zusammen mit einer volumenverteilten Kraft. Die [[Leistung (Physik)|Leistung]] des Spannungstensors an [[Geschwindigkeitsgradient#Dehn- und Schergeschwindigkeiten|Verzerrungsgeschwindigkeiten]] trägt zur [[Kontinuumsmechanik#Energiebilanz|Energiebilanz]] bei. Die Komponenten des Spannungstensors haben die [[Dimension (Größensystem)| Dimension]] M L<sup>-1</sup> T<sup> -2</sup> also [[Kraft]] pro [[Flächeninhalt|Fläche]], für die in der [[Mechanik fester Körper|Festkörpermechanik]] die Einheit [[Pascal (Einheit)#Megapascal|Megapascal]] (MPa) oder [[Newton (Einheit)|Newton]] pro [[Quadratmillimeter]] (N/mm²) üblich sind. |
||
Der Spannungstensor fasst die |
Der Spannungstensor fasst die Normalspannungen in Druckrichtung, sowie seitliche wirkende (transversale) [[Scherspannung]]en zu einem mathematischen Objekt zusammen. Verwendet wird dieser Tensor vor allem in der Physik ([[Festkörperphysik]], [[Strömungsmechanik]] und [[Klassische Mechanik]], teilweise [[Geophysik]]) und in der [[Elektrodynamik]]. |
||
== Definition == |
== Definition == |
||
[[Datei: |
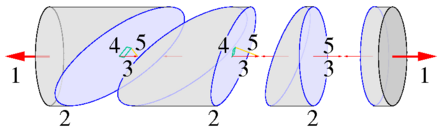
[[Datei:schnittfigur.png|mini|hochkant=2|Zylinder (grau) unter äußerer Belastung (1) mit Schnittebenen (2), Schnittspannungen (3), Schubspannungen (4) und Normalspannungen (5)]] |
||
In einer gedachten [[Schnittfläche]] durch die Materie übt die in Gedanken weggeschnittene Materie auf die verbliebene Materie eine Spannung aus, die sich als Spannungsvektor <math>\ |
In einer gedachten [[Schnittfläche]] durch die Materie übt die in Gedanken weggeschnittene Materie auf die verbliebene Materie eine Spannung aus, die sich als Spannungsvektor <math>\vec T^{(\hat n)}=\sigma_{nn}\hat{n}+\tau_{nt_1}\hat{e}_{t_1}+\tau_{nt_2}\hat{e}_{t_2}</math> aus einer Normalspannungskomponente <math>\sigma_{nn}</math> (rechtwinklig zur Schnittfläche wirkend) und zwei Schubspannungskomponenten <math>\tau_{nt_{1,2}}</math> (in der Schnittfläche wirkend) zusammensetzt, die von der Ausrichtung der Fläche abhängen, siehe Bild. Der erste Index der Koordinaten des Spannungsvektors verweist auf die Normalenrichtung der Fläche und der zweite Index auf die Wirkrichtung der Spannung. |
||
Am jeweiligen Ort schneiden sich drei solche gedachten Schnittflächen mit den Basisvektoren des Koordinatensystems |
Am jeweiligen Ort schneiden sich drei solche gedachten Schnittflächen mit den Basisvektoren des Koordinatensystems <math>\hat{e}_{1,2,3}</math> als Normalen. Die drei Spannungsvektoren in den drei Schnittflächen werden zeilenweise zum Spannungstensor zusammengefasst: |
||
:<math> |
|||
:<math>\underline{\underline{\sigma}} = \sum_{i,j=1}^{3} \sigma^{ij} \,{\underline{e}}_i \otimes {\underline{e}}_j</math>. |
|||
\vec T^{(\hat e_i)}=\sum_{j=1}^{3}\sigma_{ij}\,\hat{e}_j |
|||
\quad\rightarrow\quad |
|||
\boldsymbol{\sigma}=\sum_{i=1}^{3}\,\hat{e}_i\otimes\vec{T}^{(\hat e_i)} |
|||
=\sum_{i,j=1}^{3}\sigma_{ij}\,\hat{e}_i\otimes\hat{e}_j\,.</math> |
|||
Dabei bezeichnet <math>\otimes</math> das [[Dyadisches Produkt|dyadische Produkt]] (Tensorprodukt zweier Vektoren). |
Dabei bezeichnet <math>\otimes</math> das [[Dyadisches Produkt|dyadische Produkt]] (Tensorprodukt zweier Vektoren). |
||
In Matrizenschreibweise wird der Spannungstensor |
In Matrizenschreibweise wird der Spannungstensor in folgenden, üblichen Formen angegeben: |
||
:<math> |
:<math> |
||
\boldsymbol{\sigma} |
|||
= |
|||
\begin{bmatrix} |
|||
\begin{pmatrix} |
|||
\sigma_{x} & \tau_{xy} & \tau_{xz} \\ |
|||
\sigma_{x} &\tau_{xy} &\tau_{xz}\\ |
|||
\tau_{yx} &\sigma_{y} &\tau_{yz}\\ |
|||
\tau_{zx} &\tau_{zy} &\sigma_{z} |
|||
\end{bmatrix} |
|||
\end{pmatrix} |
|||
= |
|||
\begin{pmatrix} |
|||
\sigma_{xx} &\sigma_{xy} &\sigma_{xz}\\ |
|||
\sigma_{yx} &\sigma_{yy} &\sigma_{yz}\\ |
|||
\sigma_{zx} &\sigma_{zy} &\sigma_{zz} |
|||
\end{pmatrix} |
|||
</math> |
</math> |
||
Manchmal, wie in der linken Matrizenschreibweise, wird der Index der Normalspannungskomponente nur einfach notiert (beispielsweise σ<sub>x</sub> = σ<sub>xx</sub>), denn bei ihr ist Normalen- und Wirkrichtung gleich. Es muss jedoch gewährleistet sein, dass eine Verwechselung mit den Hauptspannungen (σ<sub>1,2,3</sub> oder σ<sub>I,II,III</sub>) ausgeschlossen ist. |
|||
Da der Spannungstensor in der [[Konfiguration (Mechanik)|Momentankonfiguration]] auf Grund der Drehimpulsbilanz für Gleichgewichtszustände symmetrisch ist (<math>\tau_{yx}=\tau_{xy}</math> etc.) besteht er nicht aus neun unabhängigen Größen, sondern nur aus sechs und kann in der [[Voigtsche Notation|Voigt’schen Notation]] als ein 6×1-Vektor geschrieben werden, wodurch die Notation deutlich vereinfacht wird: |
|||
Da der Cauchy’sche Spannungstensor in der [[Konfiguration (Mechanik)|Momentankonfiguration]] auf Grund des [[Cauchy-Eulersche Bewegungsgesetze#Zweites Cauchy-Euler’sches Bewegungsgesetz|zweiten Cauchy-Euler’schen Bewegungsgesetzes]] ([[Kontinuumsmechanik#Drehimpulsbilanz|Drehimpulsbilanz]]) [[Symmetrische Matrix|symmetrisch]] ist (<math>\tau_{yx}=\tau_{xy}</math> etc.) besteht er nicht aus neun unabhängigen Größen, sondern nur aus sechs und kann in der [[Voigtsche Notation|Voigt’schen Notation]] als ein 6×1-Vektor geschrieben werden, wodurch die Notation deutlich vereinfacht wird: |
|||
:<math> |
:<math> |
||
\vec{\sigma} = |
|||
\begin{pmatrix}\sigma_{x}\\\sigma_{y}\\\sigma_{z}\\\tau_{yz}\\\tau_{xz}\\\tau_{xy}\end{pmatrix} |
|||
</math> |
</math> |
||
== Zusammenhang mit anderen Größen == |
|||
Für [[Ideales Gas|ideale Gase]] und [[Ideale Flüssigkeit|ideale Flüssigkeiten]] reduziert sich der Spannungstensor gerade zum [[Druck (Physik)|Druck]] ''p'' multipliziert mit der [[Einheitstensor]] <math>\mathbf{1}</math>: |
|||
:<math>\boldsymbol{\sigma}^P=-p\mathbf{1}</math> |
|||
und wird '''Drucktensor''' genannt, siehe [[Eulersche Gleichungen (Strömungsmechanik)]].<ref>{{Literatur|Autor=Brandt, Dahmen|Titel=Mechanik: Eine Einführung in Experiment und Theorie|Verlag=Springer|Jahr=2004|Online=http://www.springer.com/de/book/9783662085912|Seiten=326}}</ref> Für seine Divergenz gilt nach der [[Produktregel]]: |
|||
:<math>\operatorname{div}(\boldsymbol{\sigma}^P) |
|||
=-\operatorname{grad}(p)\cdot\mathbf{1}-p\operatorname{div}(\mathbf{1}) |
|||
=-\operatorname{grad}p |
|||
.</math> |
|||
Darin bildet grad den [[Gradient (Mathematik)|Gradienten]]. |
|||
Der Maxwell’sche Spannungstensor aus der Elektrodynamik ist eine [[Untermatrix]] des [[Energie-Impuls-Tensor]]s. |
|||
== Impulsbilanz == |
|||
Wenn aus einem Körper ein Teilkörper freigeschnitten wird und dessen ''Oberfläche'' beliebig klein gewählt wird, folgt aus der Impulsbilanz, dass der Zusammenhang zwischen dem Normalenvektor an eine Schnittfläche und dem Schnittspannungsvektor linear sein muss. Das ist die Aussage des [[Cauchysches Fundamentaltheorem|Cauchy’schen Fundamentaltheorems]], mit dem [[Augustin-Louis Cauchy]] den Spannungstensor als [[linearer Operator|linearen Operator]] zwischen den Normalenvektoren und den Schnittspannungsvektoren eingeführte. |
|||
Das Volumen eines Körpers geht schneller gegen null als seine Oberfläche, weswegen Masseneffekte bei obiger Betrachtung vernachlässigt werden konnten. Geht nun das ''Volumen'' des Teilkörpers gegen null, dann zeigt sich, dass die Beschleunigung eines materiellen Punkts mit den räumlichen Spannungsanstiegen in Form der [[Divergenz eines Vektorfeldes|Divergenz]] des Spanngungstensors wächst. Das ist die Aussage des [[Cauchy-Eulersche Bewegungsgesetze#Erstes Cauchy-Eulersches Bewegungsgesetz|ersten Cauchy-Euler’schen Bewegungsgesetzes]]. |
|||
=== Cauchysches Fundamentaltheorem === |
|||
Wird ein Tetraeder mit Kantenlänge ''L'' aus einem belasteten Körper herausgeschnitten, dann übt die in Gedanken weggeschnittene Materie auf jeder Schnittfläche Spannungen aus, die über ihre Angriffsfläche nach dem Gesetz „[[Newtonsche Axiome#Zweites newtonsches Gesetz|Kraft gleich Masse mal Beschleunigung]]“ den Tetraeder beschleunigen. Weil die Masse eines kleinen Tetraeders mit ''L³'' gegen null geht, seine Oberfläche aber nur mit ''L²'', können Masseneffekte vernachlässigt werden und müssen die flächenverteilten Kräfte im [[Gleichgewicht (Physik)#Allgemeines, Kräftegleichgewicht, Momentengleichgewicht|Gleichgewicht]] sein. Das ist genau dann der Fall, wenn der Zusammenhang zwischen den Normalenvektoren und den Schnittspannungsvektoren linear ist: |
|||
:<math>\vec T^{(\vec a+b\vec c)}=\vec T^{(\vec a)}+b\vec T^{(\vec c)} |
|||
\quad\Leftrightarrow\quad |
|||
\vec T^{(\hat n)}=\boldsymbol{\sigma}^\top\cdot\hat n=\hat n\cdot\boldsymbol{\sigma} |
|||
\quad\Leftrightarrow\quad |
|||
T^{(\hat n)}_j=\sum_{i=1}^3\sigma_{ij}n_i.</math> |
|||
Darin ist |
|||
* <math>\vec T^{(\vec v)}</math> der Schnittspannungsvektor an einer Fläche mit Normalenvektor <math>\vec v</math>, |
|||
* ''b'' ein Faktor, <math>\vec a, \vec c</math> Normalenvektoren und <math>\hat n</math> ein Normaleneinheitsvektor, |
|||
* <math>\boldsymbol{\sigma}</math> der Spanngungstensor, <math>\boldsymbol{\sigma}^\top</math> seine [[Transponierte Matrix|Transponierte]], |
|||
* ''σ''<sub>ij</sub> sind die Komponenten des Spanngungstensors, ''T''<sub>j</sub> die des Spannungsvektors und ''n''<sub>i</sub> die des Normaleneinheitsvektors bezüglich eines [[Kartesische Koordinaten|kartesischen Koordinatensystems]] und |
|||
* „·“ ist das [[Skalarprodukt]] von Vektoren. |
|||
Das ist die Aussage des Cauchysch’en Fundamentaltheorems. Die Benutzung eines [[Tensor]]s stellt sicher, dass obige Zusammenhänge koordinatenunabhängig sind. |
|||
=== Erstes Cauchy-Euler’sches Bewegungsgesetz === |
|||
Das zweite [[Newtonsche Gesetze|Newton’sche Gesetz]] beschreibt die Reaktion eines [[Körper (Physik)|Körpers]] auf eine äußere [[Kraft]]. In der Realität und der Kontinuumsmechanik werden solche Kräfte immer flächig eingeleitet, d. h. in Form von auf der Oberfläche ''a'' wirkenden Spannungsvektoren: |
|||
:<math>\vec F |
|||
=\int_a \vec{T}^{(\hat n)}\;\mathrm{d}a |
|||
=\int_a \boldsymbol{\sigma}^\top\cdot\hat n\;\mathrm{d}a |
|||
=\int_v \operatorname{div}(\boldsymbol{\sigma})\;\mathrm{d}v |
|||
</math> |
|||
Im letzten Schritt wurde der [[Divergenzsatz#Folgerungen|gaußsche Integralsatz]] ausgenutzt, was bei einem realen Körper statthaft ist, wenn seine Oberfläche abschnittsweise glatt ist. So, wie die Kraft <math>\vec F</math> den Körper als Ganzes beschleunigt, so beschleunigt die [[Divergenz eines Vektorfeldes|Divergenz]] div des Spannungstensors die mit einer Dichte ρ versehenen, materiellen Punkte des Körpers: |
|||
:<math>\rho\ddot{\vec x}=\operatorname{div}(\boldsymbol{\sigma})+\rho\vec k.</math> |
|||
Darin ist <math>\ddot{\vec x}</math> die (ortsabhängige) Beschleunigung eines materiellen Punktes und <math>\vec k</math> eine eventuell zu berücksichtigende, von außen angreifende, volumenverteilte Beschleunigung wie die [[Schwerebeschleunigung]]. Dieses ''erste Cauchy-Euler’sche Bewegungsgesetz'' ist die lokale Form der [[Impulserhaltungssatz#Impulserhaltung in der Newton’schen Mechanik|Impulsbilanz]], die, wenn sie in jedem Punkt eines [[Körper (Physik)|Körpers]] erfüllt ist, sicherstellt, dass die Bewegung des Körpers als Ganzes – inklusive Verformungen – der Impulsbilanz gehorcht. |
|||
== Typen von Spannungstensoren == |
== Typen von Spannungstensoren == |
||
Beim Spannungstensor handelt es sich um ein [[Tensorfeld]], das an jedem materiellen <math>\vec X</math> oder räumlichen Punkt <math>\vec x</math> innerhalb eines Körpers definiert ist. Erstere materielle Sichtweise entspricht der [[Lagrangesche Betrachtungsweise|Lagrange’schen Darstellung]] und letztere räumliche der [[Eulersche Betrachtungsweise|Euler’schen Darstellung]]. Die Kontinuumsmechanik definiert mehrere Spannungstensoren: |
|||
Die [[Kontinuumsmechanik]] definiert mehrere Spannungstensoren: |
|||
* Den räumlichen Cauchy’schen Spannungstensor <math>\boldsymbol{\sigma}\,,</math> |
|||
* Den gewichteten Cauchy’schen Spannungstensor <math>\mathbf{S}=\operatorname{det}(\mathbf{F})\boldsymbol{\sigma}\,,</math> |
|||
* Den materiellen zweiten [[Gabrio_Piola|Piola]]-[[Gustav_Robert_Kirchhoff|Kirchhoff]]’schen Spannungstensor <math>\tilde{\mathbf{T}}=\det(\mathbf{F})\mathbf{F}^{-1}\cdot\boldsymbol{\sigma}\cdot\mathbf{F}^{\top-1} |
|||
=\mathbf{F}^{-1}\cdot\mathbf{S\cdot F}^{\top-1}\,,</math> |
|||
# den in der Ausgangskonfiguration wirkenden, im Allgemeinen unsymmetrischen, ersten Piola-Kirchhoffschen Spannungstensor <math> \mathbf{T}_{0}=\det(\mathbf{F})\mathbf{T}\mathbf{F}^\mathrm{-T}=\mathbf{S}\mathbf{F}^\mathrm{-T} </math> und |
|||
* Den materiellen, im Allgemeinen unsymmetrischen, ersten Piola-Kirchhoffschen Spannungstensor <math>\mathbf{P}=\det(\mathbf{F})\boldsymbol{\sigma}\cdot\mathbf{F}^{\top-1}=\mathbf{S\cdot F}^{\top-1}</math> und |
|||
# den in der Ausgangskonfiguration wirkenden konvektiven Spannungstensor <math> \tilde{\mathbf{t}} |
|||
* Den materiellen, im Allgemeinen unsymmetrischen, Nominalspannungstensor, der der [[Transponierte Matrix|transponierte]] erste Piola-Kirchhoff’sche Spannungstensor ist: <math>\mathbf{N}:=\mathbf{P}^\top\,.</math> Der Nominalspannungstensor beinhaltet die Spannungen bezogen auf die Ausgangsfläche und seine Komponenten heißen ''Nominalspannungen''. |
|||
=\det(\mathbf{F})\mathbf{F}^{\mathrm{T}}\mathbf{T}\mathbf{F} |
|||
* Den materiellen konvektiven Spannungstensor<ref>Bezeichnung nach Haupt (2002), S. 94, der auf {{Literatur| Autor=C. Truesdell| Titel=Die Nicht-Linearen Feldtheorien der Mechanik| Herausgeber=S. Flügge| Sammelwerk=Handbuch der Physik| Band=Bd. III/3| Verlag=Springer| Jahr=2013| ISBN=978-3-642-46017-3}} verweist.</ref> <math>\tilde{\mathbf{t}} |
|||
=\mathbf{F}^{\mathrm{T}}\mathbf{S}\mathbf{F} </math>. |
|||
=\det(\mathbf{F})\mathbf{F}^\top\cdot\boldsymbol{\sigma}\cdot\mathbf{F} |
|||
=\mathbf{F^\top\cdot S\cdot F}\,.</math> |
|||
Darin ist < |
Darin ist '''F''' der [[Deformationsgradient]], '''F'''<sup>-1</sup> seine [[Inverse Matrix|Inverse]], '''F'''<sup>T-1</sup> seine transponiert inverse und det('''F''') seine [[Determinante]]. Der Cauchy’sche Spannungstensor, der Nominalspannungstensor und der erste Piola-Kichhoff’sche Spannungstensor erfüllen die [[Kontinuumsmechanik#Impulsbilanz|Impulsbilanz]], ersterer in der räumlichen, letztere beide in der materiellen Formulierung. Bis auf den ersten Piola-Kirchhoff’schen und den Nominalspannungstensor sind alle genannten Spannungstensoren auf Grund der Drehimpulsbilanz symmetrisch. Die Tabelle fasst die Umrechnung der Tensoren zusammen. |
||
{| class="wikitable center" |
|||
== Zusammenhang mit anderen Größen == |
|||
|- |
|||
Für Gase reduziert sich der Spannungstensor gerade zum [[Druck (Physik)|Druck]] ''p'' multipliziert mit der [[Einheitsmatrix]] <math>\mathbf{1}</math>: |
|||
! !! <math>\boldsymbol{\sigma}</math>!!<math>\mathbf{S}</math>!!<math>\tilde{\mathbf{T}}</math> |
|||
:<math> |
|||
! <math>\mathbf{P}</math>!!<math>\mathbf{N}</math>!!<math>\tilde{\mathbf{t}}</math> |
|||
|- |
|||
und wird '''Drucktensor''' genannt.<ref>{{Literatur|Autor=Brandt, Dahmen|Titel=Mechanik: Eine Einführung in Experiment und Theorie|Verlag=Springer|Jahr=2004|Online={{Google Buch|BuchID=cvc9AiqAu8C}}|Seiten=326}}</ref> |
|||
! <math>\boldsymbol{\sigma}=</math> |
|||
| <math>\boldsymbol{\sigma}</math> |
|||
| <math>\frac{1}{J}\mathbf{S}</math> |
|||
| <math>\frac{1}{J}\mathbf{F}\cdot\tilde{\mathbf{T}}\cdot\mathbf{F}^\top</math> |
|||
| <math>\frac{1}{J}\mathbf{P\cdot F}^\top</math> |
|||
| <math>\frac{1}{J}\mathbf{F\cdot N}</math> |
|||
| <math>\frac{1}{J}\mathbf{F}^{\top-1}\cdot\tilde{\mathbf{t}}\cdot\mathbf{F}^{-1}</math> |
|||
|- |
|||
! <math>\mathbf{S}=</math> |
|||
| <math>J\boldsymbol{\sigma}</math> |
|||
| <math>\mathbf{S}</math> |
|||
| <math>\mathbf{F}\cdot\tilde{\mathbf{T}}\cdot\mathbf{F}^\top</math> |
|||
| <math>\mathbf{P\cdot F}^\top</math> |
|||
| <math>\mathbf{N^\top\cdot F}^\top</math> |
|||
| <math>\mathbf{F}^{\top-1}\cdot\tilde{\mathbf{t}}\cdot\mathbf{F}^{-1}</math> |
|||
|- |
|||
! <math>\tilde{\mathbf{T}}=</math> |
|||
| <math>J\mathbf{F}^{-1}\cdot\boldsymbol{\sigma}\cdot\mathbf{F}^{\top-1}</math> |
|||
| <math>\mathbf{F}^{-1}\cdot\mathbf{S\cdot F}^{\top-1}</math> |
|||
| <math>\tilde{\mathbf{T}}</math> |
|||
| <math>\mathbf{F}^{-1}\cdot\mathbf{P}</math> |
|||
| <math>\mathbf{F}^{-1}\cdot\mathbf{N}^\top</math> |
|||
| <math>\mathbf{C}^{-1}\cdot\tilde{\mathbf{t}}\cdot\mathbf{C}^{-1}</math> |
|||
|- |
|||
! <math>\mathbf{P}=</math> |
|||
| <math>J\boldsymbol{\sigma}\cdot\mathbf{F}^{\top-1}</math> |
|||
| <math>\mathbf{S\cdot F}^{\top-1}</math> |
|||
| <math>\mathbf{F}\cdot\tilde{\mathbf{T}}</math> |
|||
| <math>\mathbf{P}</math> |
|||
| <math>\mathbf{N}^\top</math> |
|||
| <math>\mathbf{F}^{\top-1}\cdot\tilde{\mathbf{t}}\cdot\mathbf{C}^{-1}</math> |
|||
|- |
|||
! <math>\mathbf{N}=</math> |
|||
| <math>J\mathbf{F}^{-1}\cdot\boldsymbol{\sigma}</math> |
|||
| <math>\mathbf{F}^{-1}\cdot\mathbf{S}</math> |
|||
| <math>\tilde{\mathbf{T}}\cdot\mathbf{F}^\top</math> |
|||
| <math>\mathbf{P}^\top</math> |
|||
| <math>\mathbf{N}</math> |
|||
| <math>\mathbf{C}^{-1}\cdot\tilde{\mathbf{t}}\cdot\mathbf{F}^{-1}</math> |
|||
|- |
|||
! <math>\tilde{\mathbf{t}}=</math> |
|||
| <math>J\mathbf{F}^\top\cdot\boldsymbol{\sigma}\cdot\mathbf{F}</math> |
|||
| <math>\mathbf{F^\top\cdot S\cdot F}</math> |
|||
| <math>\mathbf{C}\cdot\tilde{\mathbf{T}}\cdot\mathbf{C}</math> |
|||
| <math>\mathbf{F^\top\cdot P\cdot C}</math> |
|||
| <math>\mathbf{F^\top\cdot N^\top\cdot C}</math> |
|||
| <math>\tilde{\mathbf{t}}</math> |
|||
|} |
|||
Darin ist ''J'' = det('''F''') und '''C''' = '''F'''<sup>T</sup> · '''F'''. Bei [[Geometrische Linearisierung|kleinen Verzerrungen]] braucht nicht zwischen diesen Spannungstensoren unterschieden zu werden. |
|||
Der Maxwell’sche Spannungstensor aus der Elektrodynamik ist eine [[Untermatrix]] des [[Energie-Impuls-Tensor]]s. |
|||
Ihre Begründung<ref>Haupt (2000), S.331ff</ref> finden diese Spannungstensoren bei der Berechnung der spezifischen Spannungsleistung ''l''<sub>i</sup>, die in der [[Kontinuumsmechanik#Energiebilanz|Energiebilanz]] vorkommt. Damit diese bezugsysteminvariant ist, werden die [[Euklidische Transformation#Geschwindigkeiten und Beschleunigung|objektiven Zeitableitungen]] |
|||
== Der Spannungstensor am Volumenelement == |
|||
Folgende Skizze verdeutlicht dies am Beispiel eines herausgeschnittenen sehr kleinen Volumenelements für [[Kartesisches Koordinatensystem|kartesische Koordinaten]]; die Betrachtungen gelten für die rechte obere hintere Ecke: |
|||
:<math>\begin{align} |
|||
[[Datei:Spannung2.svg]] |
|||
\stackrel{\Delta}{\boldsymbol{\phi}} |
|||
:=& |
|||
\dot{\boldsymbol{\phi}}+\boldsymbol{\phi}\cdot\mathbf{l+l}^\top\cdot\boldsymbol{\phi} |
|||
\\ |
|||
\stackrel{\nabla}{\boldsymbol{\phi}} |
|||
:=& |
|||
\dot{\boldsymbol{\phi}}-\mathbf{l}\cdot\boldsymbol{\phi}-\boldsymbol{\phi}\cdot\mathbf{l}^\top |
|||
\end{align}</math> |
|||
benötigt, die mit dem [[Geschwindigkeitsgradient]] '''l''' gebildet werden. Mit den Verzerrungstensoren |
|||
In einer konkreten Schnittfläche, deren Orientierung durch ihren nach außen gerichteten Normalenvektor <math>\underline{n}</math> beschrieben wird, ergibt sich der Spannungsvektor <math>\underline{s}</math>, indem man den Spannungstensor mit dem Normalenvektor multipliziert: |
|||
:<math>\underline{s} = \underline{\underline{\sigma}}^T \cdot \underline{n}</math> |
|||
:<math>\begin{align} |
|||
bzw. für einen symmetrischen Spannungstensor: |
|||
\text{Green-Lagrange}&\quad \mathbf{E}:=\frac12(\mathbf{F^\top\cdot F-1})=\mathbf{F^\top\cdot e\cdot F} |
|||
:<math>\underline{s} = \underline{\underline{\sigma}} \cdot \underline{n}</math>. |
|||
\\ |
|||
\text{Euler-Almansi}&\quad\mathbf{e}:=\frac12(\mathbf{1-F^{\rm\top-1}\cdot F^{\rm-1}})=\mathbf{F^{\rm\top-1}\cdot E\cdot F}^{-1} |
|||
\\ |
|||
\text{Lagrange-Karni-Reiner}&\quad\mathbf{A}:=\frac12(\mathbf{1-F^{\rm-1}\cdot F^{\rm\top-1}}) |
|||
=\mathbf{F^{\rm-1}\cdot a\cdot F}^{\top-1} |
|||
\\ |
|||
\text{Euler-Karni-Reiner}&\quad\mathbf{a}:=\frac12(\mathbf{F\cdot F^\top-1})=\mathbf{F\cdot A\cdot F}^\top |
|||
\end{align}</math> |
|||
berechnen sich die Verzerrungsgeschwindigkeiten |
|||
:<math>\mathbf{d} |
|||
=\mathbf{F}^{\top-1}\cdot\dot{\mathbf{E}}\cdot\mathbf{F}^{-1} |
|||
=\stackrel{\Delta}{\mathbf{e}} |
|||
=\mathbf{F}\cdot\dot{\mathbf{A}}\cdot\mathbf{F}^\top |
|||
=\stackrel{\nabla}{\mathbf{a}} |
|||
</math> |
|||
und die spezifische Spanngungsleistung |
|||
:<math>\begin{align} |
|||
l_i |
|||
=&\frac{1}{\rho_0}\tilde{\mathbf{T}}:\dot{\mathbf{E}} |
|||
= |
|||
\frac{1}{\rho_0}\tilde{\mathbf{t}}:\dot{\mathbf{A}} |
|||
\\=& |
|||
\frac{1}{\rho}\boldsymbol{\sigma}:\mathbf{d} |
|||
= |
|||
\frac{1}{\rho}\boldsymbol{\sigma}:\stackrel{\Delta}{\mathbf{e}} |
|||
= |
|||
\frac{1}{\rho}\boldsymbol{\sigma}:\stackrel{\nabla}{\mathbf{a}} |
|||
\\=& |
|||
\frac{1}{\rho_0}\mathbf{S}:\mathbf{d} |
|||
= |
|||
\frac{1}{\rho_0}\mathbf{S}:\stackrel{\Delta}{\mathbf{e}} |
|||
= |
|||
\frac{1}{\rho_0}\mathbf{S}:\stackrel{\nabla}{\mathbf{a}} |
|||
\\=& |
|||
\frac{1}{\rho}(\mathbf{F}^{-1}\cdot\mathbf{P\cdot F}^{\top-1}):\dot{\mathbf{F}} |
|||
= |
|||
\frac{1}{\rho}\mathbf{P}:(\mathbf{F}^{\top-1}\cdot\dot{\mathbf{F}}\cdot\mathbf{F}^{-1}) |
|||
\end{align}</math> |
|||
Darin ist ρ<sub>0</sub> = ρ det('''F''') die Dichte des Materials und ρ die Dichte im verformten Körper. |
|||
== Eigensystem == |
== Eigensystem == |
||
Für Matrizen wie für Spannungstensoren kann man nach Eigenwerten <math> |
Für Matrizen wie für Spannungstensoren kann man nach Eigenwerten <math>\sigma_i</math> und Eigenvektoren <math>\hat{v}_i</math> suchen, die das [[Eigenwertproblem]] |
||
:<math>\boldsymbol{\sigma}\cdot\hat{v}_i=\sigma_i\hat{v}_i</math> |
|||
lösen. Bei den symmetrischen Spannungstensoren, und nur die sollen hier untersucht werden, sind die Eigenwerte sämtlich reell und die Eigenvektor paarweise senkrecht oder orthogonalisierbar. |
|||
=== Hauptspannungen und maximale Normalspannungen === |
|||
:<math> \mathbf{T}{\underline{v}}_i=\sigma_i{\underline{v}}_i </math> |
|||
Die Eigenwerte werden Hauptspannungen und die (auf die Länge eins normierten und deshalb mit Hut geschriebenen) Eigenvektoren Hauptspannungsrichtungen genannt, siehe [[[[Spannung (Mechanik)#Hauptspannung und Hauptspannungsrichtung|Hauptspannung und Hauptspannungsrichtung]]. |
|||
Die Eigenwerte ergeben sich aus der ''charakteristischen Gleichung'' |
Die Eigenwerte ergeben sich aus der ''[[charakteristisches Polynom|charakteristischen Gleichung]]'' |
||
:<math> |
:<math>\operatorname{det}(\boldsymbol{\sigma}-\sigma_i\mathbf{I}) |
||
= |
= |
||
-\sigma_i^3 |
-\sigma_i^3 |
||
+\ |
+\operatorname{I}_1(\boldsymbol{\sigma})\sigma_i^2 |
||
-\ |
-\operatorname{I}_2(\boldsymbol{\sigma})\sigma_i |
||
+\ |
+\operatorname{I}_3(\boldsymbol{\sigma})=0\,,</math> |
||
worin die Koeffizienten für |
worin die Koeffizienten für die [[Hauptinvariante]]n |
||
:<math>\begin{ |
:<math>\begin{align} |
||
\ |
\operatorname{I}_1(\boldsymbol{\sigma}) |
||
=& |
|||
\operatorname{Sp}(\boldsymbol{\sigma}) |
|||
\mathrm{Spur}(\mathbf{T}) |
|||
=\sigma_{xx}+\sigma_{yy}+\sigma_{zz} |
=\sigma_{xx}+\sigma_{yy}+\sigma_{zz} |
||
\\[1ex] |
\\[1ex] |
||
\ |
\operatorname{I}_2(\boldsymbol{\sigma}) |
||
=& |
|||
\frac{1}{2}[\ |
\frac{1}{2}[\operatorname{I}_1{(\boldsymbol{\sigma})}^2-\operatorname{I}_1(\boldsymbol{\sigma}^2)]=\sigma_{xx}\sigma_{yy}+\sigma_{xx}\sigma_{zz}+\sigma_{yy}\sigma_{zz}-\sigma_{xy}^2-\sigma_{xz}^2-\sigma_{yz}^2 |
||
\\[1ex] |
\\[1ex] |
||
\ |
\operatorname{I}_3(\boldsymbol{\sigma}) |
||
=& |
|||
\ |
\operatorname{det}(\boldsymbol{\sigma}) |
||
= |
|||
=\frac{1}{3}[\mathrm{I}_1(\mathbf{T}^3) |
|||
\sigma_{xx}\sigma_{yy}\sigma_{zz}+2\sigma_{xy}\sigma_{yz}\sigma_{xz} |
|||
+3\mathrm{I}_1(\mathbf{T})\mathrm{I}_2(\mathbf{T}) |
|||
-\mathrm{I}_1{(\mathbf{T})}^3] |
|||
\\[1ex] |
|||
&=&\sigma_{xx}\sigma_{yy}\sigma_{zz}+2\sigma_{xy}\sigma_{yz}\sigma_{xz} |
|||
-\sigma_{xx}\sigma_{yz}^2-\sigma_{xy}^2\sigma_{zz}-\sigma_{xz}^2\sigma_{yy} |
-\sigma_{xx}\sigma_{yz}^2-\sigma_{xy}^2\sigma_{zz}-\sigma_{xz}^2\sigma_{yy} |
||
\end{ |
\end{align}</math> |
||
stehen und die Komponenten <math> |
stehen und die Komponenten <math>\sigma_{ij}</math> die Spannungskomponenten im kartesischen x-y-z-System sind. |
||
Die Hauptspannungsrichtungen <math> |
Die ''Hauptspannungsrichtungen'' <math>\hat{v}_i</math> sind paarweise senkrecht zueinander oder orthogonalisierbar und bilden somit auch eine [[Orthonormalbasis]]. In diesem Basissystem besitzt der Spannungstensor [[Diagonalmatrix|Diagonalgestalt]]: |
||
:<math> |
:<math>\boldsymbol{\sigma}=\sum_{i=1}^3\sigma_i\hat{v}_i\otimes\hat{v}_i |
||
=\begin{pmatrix} |
|||
\sigma_1 & 0 & 0\\ |
|||
0 &\sigma_2 & 0\\ |
|||
0 & 0 &\sigma_3 |
|||
\end{pmatrix}_{\hat{v}_i\otimes\hat{v}_j} |
|||
\,.</math> |
|||
Die Beträge der Schnittspannungsvektoren |
Die Beträge der Schnittspannungsvektoren |
||
:<math> |
:<math>|\vec{T}^{(\hat n)}| |
||
= |
= |
||
\sqrt{\ |
\sqrt{(\boldsymbol{\sigma}\cdot\hat{n})\cdot(\boldsymbol{\sigma}\cdot\hat{n})} |
||
</math> |
</math> |
||
nehmen in den Hauptspannungsrichtungen <math> |
nehmen in den Hauptspannungsrichtungen <math>\hat{n}=\hat{v}_i</math> Extremwerte an. |
||
{| class="wikitable mw-collapsible mw-collapsed" |
{| class="wikitable mw-collapsible mw-collapsed" |
||
| Zeile 120: | Zeile 293: | ||
! Beweis mit [[Lagrangescher Multiplikator|Lagrange’schen Multiplikatoren]] |
! Beweis mit [[Lagrangescher Multiplikator|Lagrange’schen Multiplikatoren]] |
||
|- |
|- |
||
| Weil die Wurzelfunktion monoton mit ihrem Argument wächst, kann man einfacher die Extremwerte der Betragsquadrate suchen: |
| Weil die Wurzelfunktion monoton mit ihrem Argument wächst, kann man einfacher die Extremwerte der Betragsquadrate suchen:<br /> |
||
<math>f(\hat{n},\lambda) |
|||
<math> f(\underline{n}, \lambda) |
|||
= |
= |
||
\ |
(\boldsymbol{\sigma}\cdot\hat{n})\cdot(\boldsymbol{\sigma}\cdot\hat{n}) |
||
-\lambda (\ |
-\lambda (\hat{n}\cdot\hat{n}-1) |
||
\rightarrow |
\rightarrow |
||
\mathrm{ |
\mathrm{extr.} |
||
</math><br /> |
|||
Darin ist λ der Lagrange’sche Multiplikator für die Nebenbedingung <math>\hat{n}\cdot\hat{n}=1.</math> Im Extremum ist <math>\tfrac{\partial\Pi}{\partial\lambda}\stackrel{!}{=}0</math> und daher wie gewünscht <math>\hat n\cdot\hat n=1.</math> Desweiteren verschwindet die [[Richtungsableitung]]<br /> |
|||
<math>\frac{\mathrm{d}f}{\mathrm{d}\hat{n}}\cdot\vec{h} |
|||
:=\frac{\mathrm{d}}{\mathrm{d}s} |
|||
f(\hat{n}+s\vec{h},\lambda)|_{s=0} |
|||
=(\boldsymbol{\sigma}\cdot\vec{h})\cdot(\boldsymbol{\sigma}\cdot\hat{n}) |
|||
+(\boldsymbol{\sigma}\cdot\hat{n})\cdot(\boldsymbol{\sigma}\cdot\vec{h}) |
|||
-2\lambda\hat{n}\cdot\vec{h} |
|||
=2 (\boldsymbol{\sigma}^\top\cdot\boldsymbol{\sigma}\cdot\hat{n}-\lambda\hat{n})\cdot |
|||
\vec{h}\stackrel{\displaystyle !}{=}0</math><br /> |
|||
in allen Richtungen <math>\vec h,</math> weshalb der Vektor in den runden Klammern der [[Nullvektor]] ist und<br /> |
|||
<math>\boldsymbol{\sigma}^\top\cdot\boldsymbol{\sigma}\cdot\hat{n}=\lambda\hat{n}</math><br /> |
|||
folgt. Demnach ist <math>\hat{n}</math> Eigenvektor von <math>\boldsymbol{\sigma}^\top\cdot\boldsymbol{\sigma} |
|||
=\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}</math> und diese Vektoren stimmen mit den Eigenvektoren <math>\hat{v}_i</math> von <math>\boldsymbol{\sigma}</math> überein wegen<br /> |
|||
<math>\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}\cdot\hat{v}_i |
|||
=\boldsymbol{\sigma}\cdot\sigma_i\hat{v}_i |
|||
=\sigma_i\boldsymbol{\sigma}\cdot\hat{v}_i=\sigma_i^2\hat{v}_i\,.</math><br /> |
|||
|} |
|||
Sortiert man die Hauptspannungen so, dass <math>|\sigma_1|\ge |\sigma_2|\ge |\sigma_3|</math> gilt, dann liegt in der 1-Richtung der betraglich größte und in 3-Richtung der betraglich kleinste Schnittspannungsvektor. |
|||
Im Extremum verschwindet die Ableitung |
|||
=== Maximale Schubspannungen === |
|||
<math> \frac{\mathrm{d}f}{\mathrm{d}\underline{n}}\cdot \underline{h} |
|||
Die maximalen Schubspannungen treten in einer Ebene e auf, die senkrecht zu einer Hauptspannungsrichtung ist. Der [[Mohrscher Spannungskreis|Mohr’sche Spannungskreis]] zeigt, dass die maximale Schubspannung im 45°-Winkel zu den Hauptspannungsrichtungen in der Ebene e vorkommt und betraglich gleich der halben Differenz der entsprechenden Hauptspannungen ist. Damit resultiert für die maximale Schubspannung: |
|||
=\frac{\mathrm{d}}{\mathrm{d}s} |
|||
:<math>\sigma_1\ge\sigma_2\ge\sigma_3\quad\rightarrow\quad\tau_{\rm max}=\frac{\sigma_1-\sigma_3}{2}.</math> |
|||
f(\underline{n}+s\underline{h}, \lambda)|_{s=0} |
|||
=\mathbf{T}\underline{h}\cdot \mathbf{T}\underline{n} |
|||
+ \mathbf{T}\underline{n}\cdot\mathbf{T}\underline{h} |
|||
-2\lambda \underline{n}\cdot \underline{h} |
|||
=2 (\mathbf{T}^{\mathrm{T}}\mathbf{T}\underline{n}-\lambda \underline{n})\cdot |
|||
\underline{h}\stackrel{\displaystyle !}{=}0 |
|||
\quad\forall\quad |
|||
\underline{h}\in \mathbb{R}^3 |
|||
\rightarrow |
|||
\mathbf{T}^{\mathrm{T}}\mathbf{T}\underline{n}=\lambda \underline{n} </math> |
|||
Falls σ<sub>1</sub> = σ<sub>3</sub> ist, befindet sich der materielle Punkt unter hydrostatischem Druck und in ''keiner'' Ebene finden sich Schubspannungen. |
|||
Demnach ist <math> \underline{n} </math> Eigenvektor von <math> \mathbf{T}^{\mathrm{T}}\mathbf{T}=\mathbf{T T} </math>. Die Eigenvektoren von <math> \mathbf{T T} </math> stimmen mit den Eigenvektoren von <math> \mathbf{T} </math> überein, denn |
|||
{| class="wikitable mw-collapsible mw-collapsed" |
|||
<math> \mathbf{T T}{\underline{v}}_i |
|||
|- |
|||
=\mathbf{T}\sigma_i{\underline{v}}_i |
|||
! Beweis |
|||
=\sigma_i\mathbf{T}{\underline{v}}_i=\sigma_i^2{\underline{v}}_i </math> |
|||
|- |
|||
|Der Spannungsvektor ergibt sich aus dem Normalenvektor <math>\hat n</math> der Länge eins (und deshalb mit Hut geschrieben) und dem Spannungstensor gemäß <math>\vec T^{(\hat n)}=\boldsymbol{\sigma}^\top\cdot\hat{n}</math>. Der Anteil <math>\vec s</math> des Spannungsvektors senkrecht zur Normale kommt heraus, wenn der Anteil in Richtung der Normale abgezogen wird: <math>\vec s=\vec T^{(\hat n)}-(\vec T^{(\hat n)}\cdot\hat n)\hat n.</math> Sein Betragsquadrat ist<br /> |
|||
q.e.d. |
|||
:<math>\begin{align} |
|||
\vec s\cdot\vec s |
|||
=& |
|||
[\vec T^{(\hat n)}-(\vec T^{(\hat n)}\cdot\hat n)\hat n]^2 |
|||
= |
|||
[\boldsymbol{\sigma}^\top\cdot\hat n-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)\hat n]\cdot |
|||
[\boldsymbol{\sigma}^\top\cdot\hat n-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)\hat n]^2 |
|||
\\=& |
|||
(\boldsymbol{\sigma}^\top\cdot\hat n)\cdot(\boldsymbol{\sigma}^\top\cdot\hat n) |
|||
-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)(\boldsymbol{\sigma}^\top\cdot\hat n)\cdot\hat n |
|||
-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)(\boldsymbol{\sigma}^\top\cdot\hat n)\cdot\hat n |
|||
+(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)^2\hat n\cdot\hat n |
|||
\\=& |
|||
\hat n\cdot\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}^\top\cdot\hat n |
|||
-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)^2 |
|||
.\end{align}</math><br /> |
|||
Das Betragsquadrat gilt es unter der Nebenbedingung <math>\hat n\cdot\hat n=1</math> zu maximieren. Die Nebenbedingung wird mit einem Lagrange’schen Multiplikator ''λ'' in der Zielfunktion berücksichtigt:<br /> |
|||
<math>\Pi(\hat n,\lambda) |
|||
:= |
|||
\hat{n}\cdot\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}^\top\cdot\hat{n} |
|||
-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)^2 |
|||
+\lambda(1-\hat n\cdot\hat n) |
|||
\to\text{extr.}</math><br /> |
|||
Im Extremum ist <math>\tfrac{\partial\Pi}{\partial\lambda}\stackrel{!}{=}0</math> und daher wie gewünscht <math>\hat n\cdot\hat n=1.</math> Außerdem verschwindet die Richtungsableitung der Zielfunktion in Richtung eines beliebigen Vektors <math>\vec h:</math><br /> |
|||
<math>\begin{align} |
|||
\left.\frac{\mathrm{d}}{\mathrm{d}s}\Pi(\hat n+s\vec h,\lambda)\right|_{s=0} |
|||
=& |
|||
\vec{h}\cdot\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}^\top\cdot\hat{n} |
|||
+\hat{n}\cdot\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}^\top\cdot\vec{h} |
|||
-2(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)(\vec{h}\cdot\boldsymbol{\sigma}\cdot\hat n |
|||
+\hat{n}\cdot\boldsymbol{\sigma}\cdot\vec{h}) |
|||
-2\lambda\hat n\cdot\vec h |
|||
\\=& |
|||
2\vec{h}\cdot\{[\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}^\top |
|||
-(\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n)(\boldsymbol{\sigma}+\boldsymbol{\sigma}^\top) |
|||
-\lambda\mathbf{1}]\cdot\hat{n}\} |
|||
\stackrel{\displaystyle !}{=}\vec0 |
|||
\end{align}</math><br /> |
|||
Weil die Ableitung für alle Vektoren <math>\vec h</math> verschwinden soll, muss der Vektor in den geschweiften Klammern ein Nullvektor und der Normalenvektor Eigenvektor des Tensors in den eckigen Klammern sein. Bei einem symmetrischen Spannungstensor und mit dem Normalspannungsanteil <math>\sigma:=\hat{n}\cdot\boldsymbol{\sigma}\cdot\hat n</math> des Spannungsvektors berechnet sich:<br /> |
|||
<math>\vec0 |
|||
\stackrel{\displaystyle !}{=} |
|||
(\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}-2\sigma\boldsymbol{\sigma}-\lambda\mathbf{1})\cdot\hat n |
|||
=(\boldsymbol{\sigma}-\sigma\mathbf{1})\cdot(\boldsymbol{\sigma}-\sigma\mathbf{1})\cdot\hat n |
|||
-(\sigma^2+\lambda)\hat n |
|||
</math><br /> |
|||
Der Normalenvektor ist demnach Eigenvektor von <math>(\boldsymbol{\sigma}-\sigma\mathbf{1})^2</math>, damit auch von <math>\boldsymbol{\sigma}-\sigma\mathbf{1}</math>, und weil jeder dieser Eigenvektoren mit zugehörigem Eigenwert ''η'' wegen<br /> |
|||
<math> |
|||
(\boldsymbol{\sigma}-\sigma\mathbf{1})\cdot\hat v |
|||
=\boldsymbol{\sigma}\cdot\hat v-\sigma\hat v |
|||
=\eta\hat v |
|||
\quad\rightarrow\quad |
|||
\boldsymbol{\sigma}\cdot\hat v=(\sigma+\eta)\hat v |
|||
</math><br /> |
|||
auch Eigenvektor des Spannungstensors ist, ist die Normale Eigenvektor des Spannungstensors.<br /> |
|||
Die maximale Schubspannung tritt in einer Ebene senkrecht zur Normale auf und diese Ebene wird von den anderen beiden Eigenvektoren des Spannungstensors aufgespannt. Die maximale Schubspannung ergibt sich in dieser Ebene aus dem [[Mohrscher Spannungskreis|Mohr’schen Spannungskreis]]. Die maximale Schubspannung ist betraglich gleich groß wie die Differenz der Hauptspannungen in der Ebene und findet sich im 45°-Winkel zu den Hauptspannungsrichtungen in der Ebene. |
|||
|} |
|} |
||
Sortiert man die Hauptspannungen so, dass <math> |\sigma_1|\ge |\sigma_2|\ge |\sigma_3| </math> gilt, dann tritt in der 1-Richtung der betraglich größte und in 3-Richtung der betraglich kleinste Schnittspannungsvektor auf. |
|||
== Invarianten == |
== Invarianten == |
||
Wenn der Spannungstensor |
Wenn der Spannungstensor bei einem [[Basiswechsel (Vektorraum)|Wechsel des Basissystems]] wie in |
||
{\underline{e}}^{\mathrm{*}}_{1},\, |
|||
{\underline{e}}^{\mathrm{*}}_{2},\, |
|||
{\underline{e}}^{\mathrm{*}}_{3}\rbrace </math> ausgedrückt wird |
|||
:<math> |
:<math>\boldsymbol{\sigma} |
||
=\sum_{i,j=1}^3\sigma^{ij} |
=\sum_{i,j=1}^3\sigma^{ij}\hat{e}_i\otimes\hat{e}_j |
||
=\sum_{i,j=1}^3\sigma^{\mathrm{*}ij} |
=\sum_{i,j=1}^3\sigma^{\mathrm{*}ij}\hat{e}_i^{*} |
||
\otimes |
\otimes\hat{e}_j^{*}</math> |
||
bezüglich eines anderen Basissystems <math>\hat{e}^{*}_{1,2,3}</math> ausgedrückt wird, |
|||
ändern sich seine Komponenten von <math> \sigma^{ij} </math> nach <math> \sigma^{\mathrm{*}ij} </math> in charakteristischer Weise, so wie sich auch die Komponenten eines geometrischen Vektors beim Wechsel des Basissystems ändern. Der Betrag des Vektors ändert sich dabei aber nicht und genauso gibt es beim Spannungstensor sogenannte ''Invarianten'', die sich bei einem Wechsel des Basissystems nicht ändern. Invariant sind: |
|||
dann ändern sich seine Komponenten von <math>\sigma^{ij}</math> nach <math>\sigma^{*ij}</math> in charakteristischer Weise, so wie sich auch die Komponenten eines geometrischen Vektors beim Wechsel des Basissystems ändern. Der Betrag des Vektors ändert sich dabei aber nicht und genauso gibt es beim Spannungstensor sogenannte ''Invarianten'', die sich bei einem Basiswechsel nicht ändern. Solche invarianten oder objektiven Größen sind in der Materialtheorie von Interesse, denn jedwedes Material verhält sich bezugssysteminvariant. Invariant sind: |
|||
# die Hauptinvarianten <math> |
# die Hauptinvarianten <math>\operatorname{I}_1(\boldsymbol{\sigma})=\operatorname{Sp}(\boldsymbol{\sigma}),\operatorname{I}_2(\boldsymbol{\sigma}),\operatorname{I}_3(\boldsymbol{\sigma})=\operatorname{det}(\boldsymbol{\sigma})\,,</math> |
||
# die Hauptspannungen <math> |
# die Hauptspannungen <math>\sigma_1,\sigma_2,\sigma_3\,,</math> |
||
# die Spuren der Potenzen <math> |
# die [[Spur (Mathematik)|Spuren]] der Potenzen <math>\operatorname{I}_1(\boldsymbol{\sigma}),\operatorname{I}_1(\boldsymbol{\sigma}^2),\operatorname{I}_1(\boldsymbol{\sigma}^3),...</math> und |
||
# der Betrag <math> |
# der Betrag <math>\parallel\boldsymbol{\sigma}\parallel |
||
:=\sqrt{\ |
:=\sqrt{\boldsymbol{\sigma}:\boldsymbol{\sigma}} |
||
:=\sqrt{\ |
:=\sqrt{\operatorname{Sp}(\boldsymbol{\sigma}\cdot\boldsymbol{\sigma}^\top)} |
||
=\sqrt{\sigma_{xx}^2+\sigma_{yy}^2+\sigma_{zz}^2 |
=\sqrt{\sigma_{xx}^2+\sigma_{yy}^2+\sigma_{zz}^2 |
||
+2\sigma_{xy}^2+2\sigma_{yz}^2+2\sigma_{xz}^2} |
+2\sigma_{xy}^2+2\sigma_{yz}^2+2\sigma_{xz}^2} |
||
=\sqrt{\sigma_1^2+\sigma_2^2+\sigma_3^2} |
=\sqrt{\sigma_1^2+\sigma_2^2+\sigma_3^2}\,,</math> |
||
siehe Abschnitt [[#Eigensystem|Eigensystem]]. Von diesen Invarianten sind aber nur drei voneinander unabhängig und aus denen können dann alle anderen abgeleitet werden. Insbesondere gilt nach dem [[Satz von Vieta]]: |
siehe Abschnitt [[#Eigensystem|Eigensystem]]. Von diesen Invarianten sind aber nur drei voneinander unabhängig und aus denen können dann alle anderen abgeleitet werden. Insbesondere gilt nach dem [[Satz von Vieta]]: |
||
:<math> |
:<math>\begin{array}{l}\operatorname{I}_1(\boldsymbol{\sigma})=\sigma_1+\sigma_2+\sigma_3 |
||
\\[1ex] |
\\[1ex] |
||
\ |
\operatorname{I}_2(\boldsymbol{\sigma})=\sigma_1\sigma_2+\sigma_2\sigma_3+\sigma_3\sigma_1 |
||
\\[1ex] |
\\[1ex] |
||
\ |
\operatorname{I}_3(\boldsymbol{\sigma})=\sigma_1\sigma_2\sigma_3\end{array}\,.</math> |
||
Die [[Vergleichsspannung#Gestaltänderungshypothese (von Mises)|von Mises Vergleichsspannung]] |
Die [[Vergleichsspannung#Gestaltänderungshypothese (von Mises)|von Mises Vergleichsspannung]] |
||
:<math> |
:<math>\sigma_{v}=\sqrt{\sigma_{xx}^2+\sigma_{yy}^2+\sigma_{zz}^2 |
||
-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz} |
-\sigma_{xx}\sigma_{yy}-\sigma_{xx}\sigma_{zz}-\sigma_{yy}\sigma_{zz} |
||
+3(\sigma_{xy}^2+\sigma_{xz}^2+\sigma_{yz}^2)} |
+3(\sigma_{xy}^2+\sigma_{xz}^2+\sigma_{yz}^2)} |
||
=\sqrt{\frac32\ |
=\sqrt{\frac32\boldsymbol{\sigma}^{\mathrm{D}}\cdot\boldsymbol{\sigma}^{\mathrm{D}}}=\sqrt{-3\operatorname{I}_2(\boldsymbol{\sigma}^{\mathrm{D}})}</math> |
||
ist eine Funktion der zweiten Hauptinvariante des spurfreien '' |
ist eine Funktion der zweiten Hauptinvariante des spurfreien ''[[Spannungsdeviator]]s'' |
||
:<math> |
:<math>\boldsymbol{\sigma}^{\mathrm{D}} |
||
=\ |
=\boldsymbol{\sigma}-\frac{1}{3}\operatorname{Sp}(\boldsymbol{\sigma})\mathbf{1}\,,</math> |
||
weswegen sie auf hydrostatische Spannungen (gleich große Normalspannungen in allen drei Raumrichtungen) nicht reagiert. Die zweite Hauptinvariante des Spannungsdeviators wird oftmals mit <math> |
weswegen sie auf hydrostatische Spannungen (gleich große Normalspannungen in allen drei Raumrichtungen) nicht reagiert. Die zweite Hauptinvariante des Spannungsdeviators wird oftmals mit <math>{J}_2</math> bezeichnet. |
||
== |
== Beispiele == |
||
=== Zugversuch === |
|||
Bei einachsialem Zug in x-Richtung lautet der Spannungstensor |
|||
:<math>\boldsymbol{\sigma}=\sigma\hat{e}_x\otimes\hat{e}_x.</math> |
|||
Im statischen Gleichgewicht und in Abwesenheit einer volumenverteilten Kraft liefert die Impulsbilanz die Bedingung |
|||
:<math>\operatorname{div}(\boldsymbol{\sigma}) |
|||
=\sum_{k=1}^3 \hat{e}_k\frac{\partial}{\partial x_k}\cdot\sigma\hat{e}_x\otimes\hat{e}_x |
|||
=\frac{\partial\sigma_{xx}}{\partial x}\hat{e}_x |
|||
=\vec0 |
|||
.</math> |
|||
Im statischen Gleichgewicht ist die Zugspannung σ<sub>xx</sub> also in x-Richtung konstant. Bei [[Hookesches Gesetz|linearer Elastizität]] ist die Spannung proportional zur Normaldehnung in x-Richtung mit dem [[Elastizitätsmodul]] E als Proportionalitätskonstante: σ<sub>xx</sub> = E ε<sub>xx</sub>. Die Normaldehnung ε<sub>xx</sub> wiederum ist gleich der Ableitung der Verschiebung ''u'' in x-Richtung nach x, also: |
|||
:<math>\frac{\partial\sigma_{xx}}{\partial x} |
|||
=E\frac{\partial\varepsilon_{xx}}{\partial x} |
|||
=E\frac{\partial^2 u}{\partial x^2} |
|||
=0 |
|||
</math> |
|||
Demnach ist die Verschiebung der materiellen Punkte des Stabes in x-Richtung linear in x. |
|||
=== Eigensystem === |
|||
Der Cauchy’sche Spannungstensor habe die Form |
Der Cauchy’sche Spannungstensor habe die Form |
||
:<math>\ |
:<math>\boldsymbol{\sigma}=\begin{pmatrix} |
||
-2& 6& -4\\ |
-2& 6& -4\\ |
||
6& 0& 6\\ |
6& 0& 6\\ |
||
-4& 6& -2 |
-4& 6& -2 |
||
\end{ |
\end{pmatrix}\,\mathrm{MPa}\,\,.</math> |
||
Seine charakteristische Gleichung lautet |
Seine charakteristische Gleichung lautet |
||
:<math>\ |
:<math>\operatorname{det}\left(\boldsymbol{\sigma}-\sigma_i\mathbf{I}\right) |
||
=-\sigma_i^3 |
=-\sigma_i^3 |
||
-4\,\mathrm{MPa}\,\sigma_i^2 |
-4\,\mathrm{MPa}\,\sigma_i^2 |
||
+84{\,\mathrm{MPa}\,}^2\sigma_i |
+84{\,\mathrm{MPa}\,}^2\sigma_i |
||
-144{\,\mathrm{MPa}\,}^3 |
-144{\,\mathrm{MPa}\,}^3 |
||
=0 |
=0\,,</math> |
||
die die Lösungen |
die die Lösungen |
||
:<math>\sigma_1=6\,\mathrm{MPa}\,,\sigma_2=2\,\mathrm{MPa}\,,\sigma_3=-12\,\mathrm{MPa}\, |
:<math>\sigma_1=6\,\mathrm{MPa}\,,\sigma_2=2\,\mathrm{MPa}\,,\sigma_3=-12\,\mathrm{MPa}\,</math> |
||
besitzt. Mit dem Ansatz |
besitzt. Mit dem Ansatz |
||
:<math> |
:<math>\vec{v}_1={\left({1,}a,b\right)}^\top</math> |
||
bekommt man |
bekommt man |
||
:<math>\ |
:<math>\boldsymbol{\sigma}\vec{v}_1=\begin{pmatrix}-2& 6& -4\\ |
||
6& 0& 6\\ |
6& 0& 6\\ |
||
-4& 6& -2\end{ |
-4& 6& -2\end{pmatrix}\,\mathrm{MPa}\,\begin{pmatrix}1\\ |
||
a\\ |
a\\ |
||
b\end{ |
b\end{pmatrix}=\begin{pmatrix}-2+6a-4b\\ |
||
6+6b\\ |
6+6b\\ |
||
-4+6a-2b\end{ |
-4+6a-2b\end{pmatrix}\,\mathrm{MPa}\,\stackrel{\displaystyle !}{=}6 |
||
\,\mathrm{MPa}\, |
\,\mathrm{MPa}\,\begin{pmatrix} |
||
1\\ |
1\\ |
||
a\\ |
a\\ |
||
b\end{ |
b\end{pmatrix}</math> |
||
mit der Lösung <math> |
mit der Lösung <math>a=2,b=1</math> und der Konsequenz |
||
:<math> |
:<math>\hat{v}_1=\frac{1}{\sqrt{6}}(1,2,1)^\top\,.</math> |
||
Entsprechend ermittelt man |
Entsprechend ermittelt man |
||
:<math> |
:<math>\hat{v}_2=\frac{1}{\sqrt2}(-1,0,1)^\top, |
||
\hat{v}_3=\frac{1}{\sqrt3}(1,-1,1)^\top\,.</math> |
|||
Die Eigenvektoren sind paarweise senkrecht aufeinander. In dem Basissystem der Eigenvektoren hat der Spannungstensor Diagonalgestalt: |
Die Eigenvektoren sind paarweise senkrecht aufeinander. In dem Basissystem der Eigenvektoren hat der Spannungstensor Diagonalgestalt: |
||
:<math>\ |
:<math>\boldsymbol{\sigma} = |
||
\begin{pmatrix} |
|||
\sigma_1 & 0 & 0 |
\sigma_1 & 0 & 0\\ |
||
0 & |
0 &\sigma_2 & 0\\ |
||
0 & 0 & |
0 & 0 &\sigma_3 |
||
\end{ |
\end{pmatrix}_{\hat{v}_i\otimes\hat{v}_j} |
||
= |
= |
||
\begin{pmatrix} |
|||
6 & 0 & 0 |
6 & 0 & 0\\ |
||
0 & 2 & 0 |
0 & 2 & 0\\ |
||
0 & 0 & -12 |
0 & 0 & -12 |
||
\end{ |
\end{pmatrix}_{\hat{v}_i\otimes\hat{v}_j} |
||
\,\mathrm{MPa} |
\,\mathrm{MPa} |
||
</math> |
</math> |
||
| Zeile 274: | Zeile 530: | ||
==Einzelnachweise== |
==Einzelnachweise== |
||
<references /> |
<references /> |
||
{{Normdaten|TYP=s|GND=4316422-5}} |
|||
[[Kategorie:Kontinuumsmechanik]] |
[[Kategorie:Kontinuumsmechanik]] |
||
[[Kategorie:Mechanische Spannung]] |
[[Kategorie:Mechanische Spannung]] |
||
[[Kategorie:Feldtheorie]] |
|||
Version vom 10. November 2016, 17:31 Uhr
Ein Spannungstensor ist ein Tensor zweiter Stufe, der die mechanischen Spannungen an einem bestimmten Punkt innerhalb der Materie beschreibt. Er ist eine wesentliche Größe der Kontinuumsmechanik, in der er bei der Formulierung physikalischer Gesetze auftritt. Die Beschleunigung der Materieelemente wird durch die räumliche Änderung des Spannungstensors bewirkt – ggf. zusammen mit einer volumenverteilten Kraft. Die Leistung des Spannungstensors an Verzerrungsgeschwindigkeiten trägt zur Energiebilanz bei. Die Komponenten des Spannungstensors haben die Dimension M L-1 T -2 also Kraft pro Fläche, für die in der Festkörpermechanik die Einheit Megapascal (MPa) oder Newton pro Quadratmillimeter (N/mm²) üblich sind.
Der Spannungstensor fasst die Normalspannungen in Druckrichtung, sowie seitliche wirkende (transversale) Scherspannungen zu einem mathematischen Objekt zusammen. Verwendet wird dieser Tensor vor allem in der Physik (Festkörperphysik, Strömungsmechanik und Klassische Mechanik, teilweise Geophysik) und in der Elektrodynamik.
Definition
In einer gedachten Schnittfläche durch die Materie übt die in Gedanken weggeschnittene Materie auf die verbliebene Materie eine Spannung aus, die sich als Spannungsvektor aus einer Normalspannungskomponente (rechtwinklig zur Schnittfläche wirkend) und zwei Schubspannungskomponenten (in der Schnittfläche wirkend) zusammensetzt, die von der Ausrichtung der Fläche abhängen, siehe Bild. Der erste Index der Koordinaten des Spannungsvektors verweist auf die Normalenrichtung der Fläche und der zweite Index auf die Wirkrichtung der Spannung.
Am jeweiligen Ort schneiden sich drei solche gedachten Schnittflächen mit den Basisvektoren des Koordinatensystems als Normalen. Die drei Spannungsvektoren in den drei Schnittflächen werden zeilenweise zum Spannungstensor zusammengefasst:
Dabei bezeichnet das dyadische Produkt (Tensorprodukt zweier Vektoren).
In Matrizenschreibweise wird der Spannungstensor in folgenden, üblichen Formen angegeben:
Manchmal, wie in der linken Matrizenschreibweise, wird der Index der Normalspannungskomponente nur einfach notiert (beispielsweise σx = σxx), denn bei ihr ist Normalen- und Wirkrichtung gleich. Es muss jedoch gewährleistet sein, dass eine Verwechselung mit den Hauptspannungen (σ1,2,3 oder σI,II,III) ausgeschlossen ist.
Da der Cauchy’sche Spannungstensor in der Momentankonfiguration auf Grund des zweiten Cauchy-Euler’schen Bewegungsgesetzes (Drehimpulsbilanz) symmetrisch ist ( etc.) besteht er nicht aus neun unabhängigen Größen, sondern nur aus sechs und kann in der Voigt’schen Notation als ein 6×1-Vektor geschrieben werden, wodurch die Notation deutlich vereinfacht wird:
Zusammenhang mit anderen Größen
Für ideale Gase und ideale Flüssigkeiten reduziert sich der Spannungstensor gerade zum Druck p multipliziert mit der Einheitstensor :
und wird Drucktensor genannt, siehe Eulersche Gleichungen (Strömungsmechanik).[1] Für seine Divergenz gilt nach der Produktregel:
Darin bildet grad den Gradienten.
Der Maxwell’sche Spannungstensor aus der Elektrodynamik ist eine Untermatrix des Energie-Impuls-Tensors.
Impulsbilanz
Wenn aus einem Körper ein Teilkörper freigeschnitten wird und dessen Oberfläche beliebig klein gewählt wird, folgt aus der Impulsbilanz, dass der Zusammenhang zwischen dem Normalenvektor an eine Schnittfläche und dem Schnittspannungsvektor linear sein muss. Das ist die Aussage des Cauchy’schen Fundamentaltheorems, mit dem Augustin-Louis Cauchy den Spannungstensor als linearen Operator zwischen den Normalenvektoren und den Schnittspannungsvektoren eingeführte.
Das Volumen eines Körpers geht schneller gegen null als seine Oberfläche, weswegen Masseneffekte bei obiger Betrachtung vernachlässigt werden konnten. Geht nun das Volumen des Teilkörpers gegen null, dann zeigt sich, dass die Beschleunigung eines materiellen Punkts mit den räumlichen Spannungsanstiegen in Form der Divergenz des Spanngungstensors wächst. Das ist die Aussage des ersten Cauchy-Euler’schen Bewegungsgesetzes.
Cauchysches Fundamentaltheorem
Wird ein Tetraeder mit Kantenlänge L aus einem belasteten Körper herausgeschnitten, dann übt die in Gedanken weggeschnittene Materie auf jeder Schnittfläche Spannungen aus, die über ihre Angriffsfläche nach dem Gesetz „Kraft gleich Masse mal Beschleunigung“ den Tetraeder beschleunigen. Weil die Masse eines kleinen Tetraeders mit L³ gegen null geht, seine Oberfläche aber nur mit L², können Masseneffekte vernachlässigt werden und müssen die flächenverteilten Kräfte im Gleichgewicht sein. Das ist genau dann der Fall, wenn der Zusammenhang zwischen den Normalenvektoren und den Schnittspannungsvektoren linear ist:
Darin ist
- der Schnittspannungsvektor an einer Fläche mit Normalenvektor ,
- b ein Faktor, Normalenvektoren und ein Normaleneinheitsvektor,
- der Spanngungstensor, seine Transponierte,
- σij sind die Komponenten des Spanngungstensors, Tj die des Spannungsvektors und ni die des Normaleneinheitsvektors bezüglich eines kartesischen Koordinatensystems und
- „·“ ist das Skalarprodukt von Vektoren.
Das ist die Aussage des Cauchysch’en Fundamentaltheorems. Die Benutzung eines Tensors stellt sicher, dass obige Zusammenhänge koordinatenunabhängig sind.
Erstes Cauchy-Euler’sches Bewegungsgesetz
Das zweite Newton’sche Gesetz beschreibt die Reaktion eines Körpers auf eine äußere Kraft. In der Realität und der Kontinuumsmechanik werden solche Kräfte immer flächig eingeleitet, d. h. in Form von auf der Oberfläche a wirkenden Spannungsvektoren:
Im letzten Schritt wurde der gaußsche Integralsatz ausgenutzt, was bei einem realen Körper statthaft ist, wenn seine Oberfläche abschnittsweise glatt ist. So, wie die Kraft den Körper als Ganzes beschleunigt, so beschleunigt die Divergenz div des Spannungstensors die mit einer Dichte ρ versehenen, materiellen Punkte des Körpers:
Darin ist die (ortsabhängige) Beschleunigung eines materiellen Punktes und eine eventuell zu berücksichtigende, von außen angreifende, volumenverteilte Beschleunigung wie die Schwerebeschleunigung. Dieses erste Cauchy-Euler’sche Bewegungsgesetz ist die lokale Form der Impulsbilanz, die, wenn sie in jedem Punkt eines Körpers erfüllt ist, sicherstellt, dass die Bewegung des Körpers als Ganzes – inklusive Verformungen – der Impulsbilanz gehorcht.
Typen von Spannungstensoren
Beim Spannungstensor handelt es sich um ein Tensorfeld, das an jedem materiellen oder räumlichen Punkt innerhalb eines Körpers definiert ist. Erstere materielle Sichtweise entspricht der Lagrange’schen Darstellung und letztere räumliche der Euler’schen Darstellung. Die Kontinuumsmechanik definiert mehrere Spannungstensoren:
- Den räumlichen Cauchy’schen Spannungstensor
- Den gewichteten Cauchy’schen Spannungstensor
- Den materiellen zweiten Piola-Kirchhoff’schen Spannungstensor
- Den materiellen, im Allgemeinen unsymmetrischen, ersten Piola-Kirchhoffschen Spannungstensor und
- Den materiellen, im Allgemeinen unsymmetrischen, Nominalspannungstensor, der der transponierte erste Piola-Kirchhoff’sche Spannungstensor ist: Der Nominalspannungstensor beinhaltet die Spannungen bezogen auf die Ausgangsfläche und seine Komponenten heißen Nominalspannungen.
- Den materiellen konvektiven Spannungstensor[2]
Darin ist F der Deformationsgradient, F-1 seine Inverse, FT-1 seine transponiert inverse und det(F) seine Determinante. Der Cauchy’sche Spannungstensor, der Nominalspannungstensor und der erste Piola-Kichhoff’sche Spannungstensor erfüllen die Impulsbilanz, ersterer in der räumlichen, letztere beide in der materiellen Formulierung. Bis auf den ersten Piola-Kirchhoff’schen und den Nominalspannungstensor sind alle genannten Spannungstensoren auf Grund der Drehimpulsbilanz symmetrisch. Die Tabelle fasst die Umrechnung der Tensoren zusammen.
Darin ist J = det(F) und C = FT · F. Bei kleinen Verzerrungen braucht nicht zwischen diesen Spannungstensoren unterschieden zu werden.
Ihre Begründung[3] finden diese Spannungstensoren bei der Berechnung der spezifischen Spannungsleistung li, die in der Energiebilanz vorkommt. Damit diese bezugsysteminvariant ist, werden die objektiven Zeitableitungen
benötigt, die mit dem Geschwindigkeitsgradient l gebildet werden. Mit den Verzerrungstensoren
berechnen sich die Verzerrungsgeschwindigkeiten
und die spezifische Spanngungsleistung
Darin ist ρ0 = ρ det(F) die Dichte des Materials und ρ die Dichte im verformten Körper.
Eigensystem
Für Matrizen wie für Spannungstensoren kann man nach Eigenwerten und Eigenvektoren suchen, die das Eigenwertproblem
lösen. Bei den symmetrischen Spannungstensoren, und nur die sollen hier untersucht werden, sind die Eigenwerte sämtlich reell und die Eigenvektor paarweise senkrecht oder orthogonalisierbar.
Hauptspannungen und maximale Normalspannungen
Die Eigenwerte werden Hauptspannungen und die (auf die Länge eins normierten und deshalb mit Hut geschriebenen) Eigenvektoren Hauptspannungsrichtungen genannt, siehe [[Hauptspannung und Hauptspannungsrichtung.
Die Eigenwerte ergeben sich aus der charakteristischen Gleichung
worin die Koeffizienten für die Hauptinvarianten
stehen und die Komponenten die Spannungskomponenten im kartesischen x-y-z-System sind.
Die Hauptspannungsrichtungen sind paarweise senkrecht zueinander oder orthogonalisierbar und bilden somit auch eine Orthonormalbasis. In diesem Basissystem besitzt der Spannungstensor Diagonalgestalt:
Die Beträge der Schnittspannungsvektoren
nehmen in den Hauptspannungsrichtungen Extremwerte an.
| Beweis mit Lagrange’schen Multiplikatoren |
|---|
| Weil die Wurzelfunktion monoton mit ihrem Argument wächst, kann man einfacher die Extremwerte der Betragsquadrate suchen:
|
Sortiert man die Hauptspannungen so, dass gilt, dann liegt in der 1-Richtung der betraglich größte und in 3-Richtung der betraglich kleinste Schnittspannungsvektor.
Maximale Schubspannungen
Die maximalen Schubspannungen treten in einer Ebene e auf, die senkrecht zu einer Hauptspannungsrichtung ist. Der Mohr’sche Spannungskreis zeigt, dass die maximale Schubspannung im 45°-Winkel zu den Hauptspannungsrichtungen in der Ebene e vorkommt und betraglich gleich der halben Differenz der entsprechenden Hauptspannungen ist. Damit resultiert für die maximale Schubspannung:
Falls σ1 = σ3 ist, befindet sich der materielle Punkt unter hydrostatischem Druck und in keiner Ebene finden sich Schubspannungen.
| Beweis |
|---|
| Der Spannungsvektor ergibt sich aus dem Normalenvektor der Länge eins (und deshalb mit Hut geschrieben) und dem Spannungstensor gemäß . Der Anteil des Spannungsvektors senkrecht zur Normale kommt heraus, wenn der Anteil in Richtung der Normale abgezogen wird: Sein Betragsquadrat ist Das Betragsquadrat gilt es unter der Nebenbedingung zu maximieren. Die Nebenbedingung wird mit einem Lagrange’schen Multiplikator λ in der Zielfunktion berücksichtigt: |
Invarianten
Wenn der Spannungstensor bei einem Wechsel des Basissystems wie in
bezüglich eines anderen Basissystems ausgedrückt wird, dann ändern sich seine Komponenten von nach in charakteristischer Weise, so wie sich auch die Komponenten eines geometrischen Vektors beim Wechsel des Basissystems ändern. Der Betrag des Vektors ändert sich dabei aber nicht und genauso gibt es beim Spannungstensor sogenannte Invarianten, die sich bei einem Basiswechsel nicht ändern. Solche invarianten oder objektiven Größen sind in der Materialtheorie von Interesse, denn jedwedes Material verhält sich bezugssysteminvariant. Invariant sind:
- die Hauptinvarianten
- die Hauptspannungen
- die Spuren der Potenzen und
- der Betrag
siehe Abschnitt Eigensystem. Von diesen Invarianten sind aber nur drei voneinander unabhängig und aus denen können dann alle anderen abgeleitet werden. Insbesondere gilt nach dem Satz von Vieta:
Die von Mises Vergleichsspannung
ist eine Funktion der zweiten Hauptinvariante des spurfreien Spannungsdeviators
weswegen sie auf hydrostatische Spannungen (gleich große Normalspannungen in allen drei Raumrichtungen) nicht reagiert. Die zweite Hauptinvariante des Spannungsdeviators wird oftmals mit bezeichnet.
Beispiele
Zugversuch
Bei einachsialem Zug in x-Richtung lautet der Spannungstensor
Im statischen Gleichgewicht und in Abwesenheit einer volumenverteilten Kraft liefert die Impulsbilanz die Bedingung
Im statischen Gleichgewicht ist die Zugspannung σxx also in x-Richtung konstant. Bei linearer Elastizität ist die Spannung proportional zur Normaldehnung in x-Richtung mit dem Elastizitätsmodul E als Proportionalitätskonstante: σxx = E εxx. Die Normaldehnung εxx wiederum ist gleich der Ableitung der Verschiebung u in x-Richtung nach x, also:
Demnach ist die Verschiebung der materiellen Punkte des Stabes in x-Richtung linear in x.
Eigensystem
Der Cauchy’sche Spannungstensor habe die Form
Seine charakteristische Gleichung lautet
die die Lösungen
besitzt. Mit dem Ansatz
bekommt man
mit der Lösung und der Konsequenz
Entsprechend ermittelt man
Die Eigenvektoren sind paarweise senkrecht aufeinander. In dem Basissystem der Eigenvektoren hat der Spannungstensor Diagonalgestalt:
woran man die Invarianz seiner Spur prüfen kann.
Literatur
- H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.
- P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2000, ISBN 3-540-66114-X.
Einzelnachweise
- ↑ Brandt, Dahmen: Mechanik: Eine Einführung in Experiment und Theorie. Springer, 2004, S. 326 (springer.com).
- ↑ Bezeichnung nach Haupt (2002), S. 94, der auf C. Truesdell: Die Nicht-Linearen Feldtheorien der Mechanik. In: S. Flügge (Hrsg.): Handbuch der Physik. Band III/3. Springer, 2013, ISBN 978-3-642-46017-3. verweist.
- ↑ Haupt (2000), S.331ff

















































































![{\displaystyle {\begin{aligned}\operatorname {I} _{1}({\boldsymbol {\sigma }})=&\operatorname {Sp} ({\boldsymbol {\sigma }})=\sigma _{xx}+\sigma _{yy}+\sigma _{zz}\\[1ex]\operatorname {I} _{2}({\boldsymbol {\sigma }})=&{\frac {1}{2}}[\operatorname {I} _{1}{({\boldsymbol {\sigma }})}^{2}-\operatorname {I} _{1}({\boldsymbol {\sigma }}^{2})]=\sigma _{xx}\sigma _{yy}+\sigma _{xx}\sigma _{zz}+\sigma _{yy}\sigma _{zz}-\sigma _{xy}^{2}-\sigma _{xz}^{2}-\sigma _{yz}^{2}\\[1ex]\operatorname {I} _{3}({\boldsymbol {\sigma }})=&\operatorname {det} ({\boldsymbol {\sigma }})=\sigma _{xx}\sigma _{yy}\sigma _{zz}+2\sigma _{xy}\sigma _{yz}\sigma _{xz}-\sigma _{xx}\sigma _{yz}^{2}-\sigma _{xy}^{2}\sigma _{zz}-\sigma _{xz}^{2}\sigma _{yy}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55c6b29fac3af1ad1ed1327203494cc9810f7526)

















![{\displaystyle {\begin{aligned}{\vec {s}}\cdot {\vec {s}}=&[{\vec {T}}^{({\hat {n}})}-({\vec {T}}^{({\hat {n}})}\cdot {\hat {n}}){\hat {n}}]^{2}=[{\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}}-({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}}){\hat {n}}]\cdot [{\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}}-({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}}){\hat {n}}]^{2}\\=&({\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}})\cdot ({\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}})-({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}})({\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}})\cdot {\hat {n}}-({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}})({\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}})\cdot {\hat {n}}+({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}})^{2}{\hat {n}}\cdot {\hat {n}}\\=&{\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}}-({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}})^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c377fd1de08e033ba9374698d749dbe70d78246)



![{\displaystyle {\begin{aligned}\left.{\frac {\mathrm {d} }{\mathrm {d} s}}\Pi ({\hat {n}}+s{\vec {h}},\lambda )\right|_{s=0}=&{\vec {h}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}}+{\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {\sigma }}^{\top }\cdot {\vec {h}}-2({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}})({\vec {h}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}}+{\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\vec {h}})-2\lambda {\hat {n}}\cdot {\vec {h}}\\=&2{\vec {h}}\cdot \{[{\boldsymbol {\sigma }}\cdot {\boldsymbol {\sigma }}^{\top }-({\hat {n}}\cdot {\boldsymbol {\sigma }}\cdot {\hat {n}})({\boldsymbol {\sigma }}+{\boldsymbol {\sigma }}^{\top })-\lambda \mathbf {1} ]\cdot {\hat {n}}\}{\stackrel {\displaystyle !}{=}}{\vec {0}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29cde2f77984313530299963ab532dad14025e4f)














![{\displaystyle {\begin{array}{l}\operatorname {I} _{1}({\boldsymbol {\sigma }})=\sigma _{1}+\sigma _{2}+\sigma _{3}\\[1ex]\operatorname {I} _{2}({\boldsymbol {\sigma }})=\sigma _{1}\sigma _{2}+\sigma _{2}\sigma _{3}+\sigma _{3}\sigma _{1}\\[1ex]\operatorname {I} _{3}({\boldsymbol {\sigma }})=\sigma _{1}\sigma _{2}\sigma _{3}\end{array}}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e268c2e31f5d8a0277ce596c09330a6761ad7e69)














