Archimedische Spirale

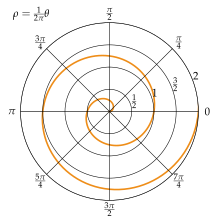
Die archimedische Spirale (auch arithmetische Spirale) ist die einfachste aller Spiralen. Sie entsteht, wenn bei einer Drehbewegung der Radius proportional zum Drehwinkel wächst:
mit .
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Die Darstellung als Parameterkurve in kartesischen Koordinaten lautet:[1]
- .
Die Länge eines Bogenstücks von bis ist
- oder kurz:
Die Gesamtlänge der Spirale von bis ist folglich
Der Flächeninhalt, die bei der ersten Umdrehung eingeschlossen wird, ist
während bei der n-ten Umdrehung der Flächeninhalt
zusätzlich eingeschlossen wird.[2]

Die Krümmung berechnet sich in Abhängigkeit vom Drehwinkel wie folgt:[3]
Neben der obigen Darstellung als Parameterkurve lässt sich die archimedische Spirale auch als Gleichung beschreiben:[1]
„Windungsabstand“[Bearbeiten | Quelltext bearbeiten]
Jeder vom Koordinatenursprung ausgehende Strahl schneidet aufeinander folgende Windungen der archimedischen Spirale in Punkten mit dem konstanten Abstand (siehe Abbildung rechts). Daher kommt auch die Bezeichnung als „arithmetische Spirale“.
Diese besondere Eigenschaft der archimedischen Spirale wird oft so ausgedrückt, dass ihr Windungsabstand konstant sei. Diese Sprechweise kann allerdings leicht missverstanden werden, da es sich hier nicht um einen konstanten Abstand zwischen Kurven im Sinne von Parallelkurven handelt. Eine Spirale, deren Windungen tatsächlich konstanten Abstand in letzterem Sinn haben, wäre die Kreisevolvente.
Tangenteneigenschaft[Bearbeiten | Quelltext bearbeiten]
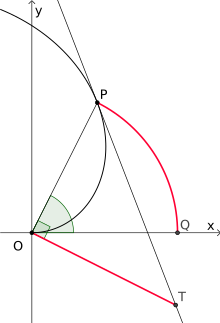
Gegeben ist ein Punkt P mit zugehörigen Radius OP und dem Drehwinkel . Die Tangente an die Spirale durch P schneidet dann die in O errichtete Senkrechte zu OP in einem Punkt T. Dann ist der zum Drehwinkel gehörige Kreisbogen PQ genau so lang wie die Strecke OT, das heißt, es gilt:[4]
Quadratur des Kreises und Winkelteilung[Bearbeiten | Quelltext bearbeiten]



Aufgrund ihrer Definition, nach der der Abstand eines Kurvenpunktes vom Koordinatenursprung proportional zum Drehwinkel ist, eignet sich die archimedische Spirale zur Teilung eines Winkels in n gleiche Teile und zur Quadratur des Kreises. Sie ist damit sowohl eine Trisektrix (n=3) als auch eine Quadratrix. Beide Probleme sind mit Zirkel und Lineal alleine nicht lösbar, lässt man jedoch die archimedische Spirale als einziges weiteres Hilfsmittel zu, so werden sie lösbar.
Zur Teilung eines Winkels BAC in n gleich große Teile erzeugt man zuerst über seinem Schenkel AB eine archimedische Spirale. Der Schenkel fungiert hierbei als x-Achse mit der Winkelspitze A als Koordinatenursprung. Die Strecke von der Winkelspitze bis zum Schnittpunkt D der Spirale mit dem anderen Winkelschenkel unterteilt man nun in n gleich lange Teile. Mit Hilfe des Strahlensatzes lässt sich dies nur mit Zirkel und Lineal bewerkstelligen, dazu zeichnet man einen weiteren Strahl von der Winkelspitze A und trägt an diesem von der Winkelspitze aus n gleich lange Strecken mit dem Zirkel ab. Dann verbindet man den Endpunkt der letzten Strecke mit dem Punkt D und Winkelschenkel und zeichnet Parallelen zu dieser Strecke durch die n-1 weiteren Streckenenden auf dem Strahl von der Winkelspitze A. Die Schnittpunkte der Parallelen mit Winkelschenkel AC unterteilen die Strecke AD in n gleich lange Teilstrecken. Nun konstruiert man n-1 Kreise, die die Winkelspitze A als Mittelpunkt haben und durch die n-1 Endpunkte der Teilstrecken von AD gehen. Schließlich verbindet man die n-1 Schnittpunkte der n-1 Kreise mit der Spiralen mit der Winkelspitze A und erhält so eine Unterteilung des Winkels BAC in n gleiche große Winkel.[4][5]
Zur Quadratur eines Kreises mit Radius r konstruiert man zunächst zwei senkrecht aufeinander stehende Koordinatenachsen durch seinen Mittelpunkt M und erzeugt eine archimedische Spirale in diesem Koordinatensystem. Die Spirale schneidet die y-Achse in einem Punkt E und die Länge der Strecke ME beträgt Längeneinheiten, da der zugehörige Drehwinkel der Spirale beträgt. Dann besitzt das Rechteck mit dem Kreisdurchmesser 2r als Länge und |ME| denselbe Flächeninhalt wie der Kreis. Mit Hilfe des Höhensatzes von Euklid lässt sich das Rechteck dann in ein flächengleiches Quadrat transformieren.[5]
Archimedes selbst verwendete zur Quadratur des Kreises eine andere Methode. Er konstruierte die Spirale zunächst für eine volle Umdrehung in einem Koordinatensystem mit Ursprung O, so dass diese positive Hälfte der x-Achse in P schneidet. Die Tangente der Spirale im Punkt P schneidet die y-Achse in T und das rechtwinklige Dreieck OPT ist flächengleich zum Kreis mit Mittelpunkt O und Radius OP. Dieses Dreieck lässt sich durch Halbierung einer der beiden Katheten leicht in einen flächengleiches Rechteck umwandeln, welches sich wie oben mit Hilfe des Höhensatzes von Euklid in ein flächengleiches Quadrat transformieren lässt.[6]
Historisches[Bearbeiten | Quelltext bearbeiten]
Archimedes beschrieb die nach ihm benannte Spirale 225 v. Chr. in seiner Abhandlung Über Spiralen, sie war allerdings schon vorher seinem Freund und Zeitgenossen Konon von Samos bekannt, der als ihr Entdecker gilt. Im 4. Jahrhundert n. Chr. wurde sie von Pappos untersucht. Die allgemeine Bestimmung der Spirallänge gelang Isaac Barrow 1670.[7][8]
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Es gibt verschiedene Verallgemeinerungen der ursprünglich von Archimedes beschrieben Spirale, für die in der Literatur auch oft archimedische Spiralen als Sammelbegriff verwendet wird. Hierbei wird die ursprüngliche Gleichung zu mit erweitert. Für erhält man die gewöhnliche Spirale des Archimedes. Der Fall wird auch als fermatsche Spirale bezeichnet, der Fall als Lituus-Spirale und der Fall als hyperbolische Spirale. Generell können sich diese Spiralen in Eigenschaften und Aussehen deutlich von der ursprünglichen archimedischen Spirale unterscheiden.
Anwendungen[Bearbeiten | Quelltext bearbeiten]


Viele Speichermedien verwenden zumindest approximativ das Prinzip der archimedischen Spirale, so rollen sich Speicherbänder (z. B. Audio- und Videokassetten) in Form einer Spirale auf. Spuren auf Schallplatten oder CDs sind ebenfalls in Form einer archimedischen Spirale angeordnet, dies ermöglicht es dem Lesekopf, ohne Unterbrechung durch einen Spurwechsel beliebig viele Daten linear (sequentiell) zu lesen.
Festplattenlaufwerke für wahlfreien Zugriff verwenden dagegen seit Beginn Blöcke/Kreissegmente auf konzentrisch angeordneten Kreisen.
Literatur[Bearbeiten | Quelltext bearbeiten]
- Dörte Haftendorn: Kurven erkunden und verstehen. Springer, 2016, ISBN 978-3-658-14748-8, S. 221–223
- D.D.Sokolov: Archimedean spiral. In Encyclopaedia of Mathematics, Band 1, S. 240
- Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA 2010, ISBN 978-0-88385-348-1, S. 145–146 (Auszug (Google))
- Janos Aczel, Claudi Alsina: Trisection of Angles, Classical Curves, and Functional Equations. Mathematics Magazine, Vol. 71, No. 3 (Juni 1998), S. 182–189 (JSTOR:2691201)
- Alexander Ostermann, Gerhard Wanner: Geometry by Its History. Springer, 2012, ISBN 978-3-642-29163-0, S. 81-82
- Midhat J. Gazalé: Gnomon: From Pharaohs to Fractals. Princeton University Press, 1999, ISBN 978-0-691-00514-0, S. 168–171
- Martin Gardner: The Unexpected Hanging, and Other Mathematical Diversions. University of Chicago Press, 1969, S. 103–107
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Eric W. Weisstein: Archimedean spiral. In: MathWorld (englisch).
- John J. O’Connor, Edmund F. Robertson: Spiral of Archimedes. In: MacTutor History of Mathematics archive (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b J. W. Rutter: Geometry of Curves. CRC Press, 2000, S. 71
- ↑ Dietmar Herrmann: Die antike Mathematik: Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. Springer, 2014, ISBN 978-3-642-37612-2, S. 181-187
- ↑ J. W. Rutter: Geometry of Curves. CRC Press, 2000, S. 149
- ↑ a b Alexander Ostermann, Gerhard Wanner: Geometry by Its History. Springer, 2012, ISBN 978-3-642-29163-0, S. 81-82
- ↑ a b Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA 2010, ISBN 978-0-88385-348-1, S. 145–146 (Auszug (Google))
- ↑ Jean-Paul Delahaye: π — Die Story. Springer, 2013, ISBN 978-3-0348-5085-8, S. 75
- ↑ Udo Hebisch: Isaac Barrow. TU Bergakademie Freiberg, abgerufen am 5. Januar 2023.
- ↑ Udo Hebisch: Archimedische Spirale. TU Bergakademie Freiberg, abgerufen am 5. Januar 2023.







![{\displaystyle {\frac {a}{2}}\left[\varphi \,{\sqrt {1+\varphi ^{2}}}+\ln \left(\varphi +{\sqrt {1+\varphi ^{2}}}\right)\right]_{\varphi _{1}}^{\varphi _{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddf8d5e1cc73e66c0fd656c90d457db98defa2f3)
![{\displaystyle {\frac {a}{2}}\left[\varphi \,{\sqrt {1+\varphi ^{2}}}+\operatorname {arsinh} \varphi \right]_{\varphi _{1}}^{\varphi _{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17e6fd40fc450d8e32c533b8054cbf00c4ac8fb8)


![{\displaystyle {\frac {a}{2}}\left[\varphi \,{\sqrt {1+\varphi ^{2}}}+\ln \left(\varphi +{\sqrt {1+\varphi ^{2}}}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f46d4800b7f28600abec47c8a3509519a235ef6)
















