Sehnenviereck

Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Kreis liegen, dem Umkreis des Vierecks. Folglich sind alle Seiten des Sehnenvierecks Sehnen des Umkreises. Üblicherweise meint man mit Sehnenviereck ein nicht-überschlagenes Sehnenviereck; es ist notwendigerweise konvex.
Das gleichschenklige Trapez, das Rechteck und das Quadrat sind besondere Sehnenvierecke.
Sätze[Bearbeiten | Quelltext bearbeiten]
Für jedes Sehnenviereck gilt der Sehnensatz:
- Die Produkte je zweier gegenüberliegender Diagonalenabschnitte sind gleich groß. Das heißt, wenn der Schnittpunkt der beiden Diagonalen und ist, so gilt .
Die folgenden Sätze gelten nur für nicht-überschlagene Sehnenvierecke ABCD:
- Gegenüberliegende Winkel ergänzen sich zu 180°, also .
- Satz von Ptolemäus: Die Summe der Produkte gegenüberliegender Seiten des Sehnenvierecks ist gleich dem Produkt der Diagonalen: .
Eigenschaften[Bearbeiten | Quelltext bearbeiten]
Winkelsummen[Bearbeiten | Quelltext bearbeiten]

Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel 180° (Abbildung 1).
Der Beweis ergibt sich unmittelbar aus dem Kreiswinkelsatz, da zwei gegenüberliegende Winkel des Sehnenvierecks Umfangswinkel über zwei komplementären Kreisbögen sind, deren Mittelpunktswinkel sich zu 360° ergänzen. Da Umfangswinkel halb so groß sind wie Mittelpunktswinkel über dem gleichen Bogen, müssen sich die Umfangswinkel zu 360°/2 = 180° ergänzen.
Ein anderer Beweis findet sich im Beweisarchiv.
Die Umkehrung dieser Aussage stimmt auch, d. h. ist in einem Viereck die Summe gegenüberliegender Winkel 180°, dann ist es ein Sehnenviereck.
Orthogonale Linien[Bearbeiten | Quelltext bearbeiten]
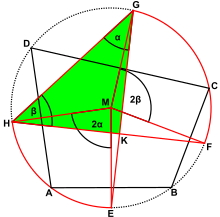
Eine weitere Eigenschaft im Sehnenviereck beschreibt der nachfolgende Satz (Abbildung 2).
Ist ein Sehnenviereck und sind , , und die Mittelpunkte der Kreisbögen über den Seiten des Sehnenvierecks, so sind die Verbindungslinien und orthogonal zueinander.
Der Beweis verwendet ebenfalls den Kreiswinkelsatz. Die Umkreisbögen zwischen und sowie zwischen und umfassen zusammen einen Winkel von 180°, weil sie jeweils die Hälfte der Bögen über den Vierecksseiten , , und enthalten.
Nach dem Kreiswinkelsatz sind die Umfangswinkel und jeweils halb so groß wie die zugehörigen Mittelpunktswinkel der Kreisbögen und .
Folglich gilt , also sind wegen der Innenwinkelsumme 180° im Dreieck auch die Strecken und orthogonal zueinander.[1]
Einbeschriebene Raute[Bearbeiten | Quelltext bearbeiten]

Gegeben sei ein Sehnenviereck , bei dem sich die Verlängerungen von zwei gegenüberliegenden Seiten jeweils in bzw. schneiden.
Dann ist das Viereck , dessen Eckpunkte die Schnittpunkte der Winkelhalbierenden durch und mit den Seiten von sind, stets eine Raute (Abbildung 3).
Beweis:
Aus den Eigenschaften des Sehnenvierecks folgt, dass die Winkel und gleich groß sind. Die Dreiecke und sind ähnlich zueinander, da sie in den obigen Winkeln und dem halben Winkel übereinstimmen. Daraus folgt, dass die Winkel und gleich groß sind. Da und Scheitelwinkel sind, haben auch sie dieselbe Weite. Damit sind wegen der Ähnlichkeit von und die Winkel und ebenfalls gleich groß. Also ist ein gleichschenkliges Dreieck und somit die Winkelhalbierende zugleich die Mittelsenkrechte von . Da und auf dieser Mittelsenkrechten liegen, haben sie denselben Abstand von und .
In analoger Vorgehensweise lässt sich schließen, dass und denselben Abstand von und haben.
Damit ist gezeigt, dass das Viereck eine Raute ist.[2][3]
Entstehung aus Winkelhalbierenden[Bearbeiten | Quelltext bearbeiten]

Die Halbierenden der Innenwinkel eines beliebigen Vierecks umschließen ein Sehnenviereck (Abbildung 4).
Beweis:
Aus den Eigenschaften der Winkelsumme und der Scheitelwinkel folgt
und
- .
Aus der Summe
folgt dann aufgrund der Eigenschaft gegenüberliegender Winkel im Sehnenviereck die Behauptung.
Hinweis: Mit analoger Beweisführung gilt die obige Aussage auch für die Außenwinkel.[4]
Formeln[Bearbeiten | Quelltext bearbeiten]
| Mathematische Formeln zum Sehnenviereck | ||
|---|---|---|
| Flächeninhalt | mit | 
|
| Länge der Diagonalen | ||
| Umkreisradius | ||
| Innenwinkel | ||
Die zuerst genannte Formel für den Flächeninhalt ist eine Verallgemeinerung des Satz des Heron für Dreiecke und wird auch als Satz von Brahmagupta oder Formel von Brahmagupta bezeichnet. Hierbei fasst man ein Dreieck als ein ausgeartetes Sehnenviereck auf, dessen vierte Seite die Länge 0 besitzt, d. h. zwei seiner Eckpunkte liegen aufeinander. Die Formel von Brahmagupta kann zur Formel von Bretschneider verallgemeinert werden, diese fügt Brahmaguptas Formel einen Korrekturterm, der im Falle eines Sehnenvierecks 0 ist, hinzu und gilt dann für beliebige Vierecke.
Ein Viereck mit festen, geordneten Seitenlängen hat genau dann den größtmöglichen Flächeninhalt, wenn es ein Sehnenviereck ist. Ebenso hat ein Vieleck genau dann den größten Flächeninhalt, wenn es ein Sehnenvieleck ist.[5]
Weitere Formeln[Bearbeiten | Quelltext bearbeiten]
Nach dem Satz des Pythagoras gilt für die Flächeninhalte der Dreiecke ABM, BCM, CDM und DAM
- und entsprechend
Der Flächeninhalt des Sehnenvierecks ABCD ist die Summe dieser 4 Flächeninhalte, also gilt
Bezeichnet man die Mittelpunktswinkel, die den Seiten , , , gegenüber liegen, mit , , , , dann gilt nach der Definition von Sinus und Kosinus
- und , also . Aus der Formel für die Doppelwinkelfunktionen folgt
- und entsprechend
Einsetzen in die Formel für den Flächeninhalt ergibt[6]
Gleichungen[Bearbeiten | Quelltext bearbeiten]
Für die Innenwinkel eines Sehnenvierecks gelten folgende Gleichungen:[7]
Für den Schnittwinkel der Diagonalen gilt:
Für den Schnittwinkel der Seiten a und c gilt:
Sehnentangentenviereck[Bearbeiten | Quelltext bearbeiten]
Spezielle Eigenschaften[Bearbeiten | Quelltext bearbeiten]

Ist ein Sehnenviereck auch zugleich ein Tangentenviereck, so wird es Sehnentangentenviereck genannt. Es besitzt sowohl einen Inkreis als auch einen Umkreis. Da die Konstruktion eines Sehnentangentenvierecks aufwändiger ist als die eines reinen Sehnen-, bzw. Tangentenvierecks, liefert der nachfolgende Satz ein Kriterium, welches die Konstruktion erleichtert:
Ein Tangentenviereck ist genau dann ein Sehnentangentenviereck, wenn die Verbindungsstrecken gegenüberliegender Berührpunkte des Inkreises senkrecht aufeinander stehen.
Beweis:
Zu zeigen ist, dass das Tangentenviereck genau dann zugleich ein Sehnenviereck ist, wenn gilt.
Anders ausgedrückt ist somit zu zeigen:
Da die beiden Dreiecke und gleichschenklig sind, haben die Winkel und jeweils die Weite und die Winkel und jeweils die Weite .
Das Viereck hat die Innenwinkelsumme
- .
Das Viereck hat die Innenwinkelsumme
- .
Nach Addition dieser beiden Gleichungen erhält man:
Also ist genau dann, wenn , was zu zeigen war.
Vereinfachte Flächeninhaltsberechnung[Bearbeiten | Quelltext bearbeiten]
Aus der Flächeninhaltsformel für Sehnenvierecke und der Halbumfangsformel für Tangentenvierecke nach dem Satz von Pitot folgt speziell für Sehnentangentenvierecke die vereinfachte Flächeninhaltsformel
- .[8]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
- I. N. Bronstein, K. A. Semendjajev, G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik. 7., vollständig überarbeitete und ergänzte Auflage. Verlag Harri Deutsch, Frankfurt am Main 2008, ISBN 978-3-8171-2007-9.
- H. Fenkner, K. Holzmüller: Mathematisches Unterrichtswerk. Nach den Richtlinien für die Lehrpläne der höheren Schulen Preußens neu bearbeitet von Dr. Karl Holzmüller. Geometrie. Ausgabe A in 2 Teilen. 12. Auflage. I. Teil. Verlag von Otto Salle, Berlin 1926.
- Theophil Lambacher, Wilhelm Schweizer (Hrsg.): Lambacher-Schweizer. Mathematisches Unterrichtswerk für höhere Schulen. Geometrie. Ausgabe E. Teil 1. 15. Auflage. Ernst Klett Verlag, Stuttgart 1965.
- Harald Scheid (Hrsg.): DUDEN: Rechnen und Mathematik. 4., völlig neu bearbeitete Auflage. Bibliographisches Institut, Mannheim / Wien / Zürich 1985, ISBN 3-411-02423-2.
- Guido Walz [Red.]: Lexikon der Mathematik in sechs Bänden. 5. Band: Sed bis Zyl. Spektrum Akademischer Verlag, Heidelberg / Berlin 2002, ISBN 3-8274-0437-1.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Beweis des Satzes von Ptolemäus (mit Umkehrung) mit geometrischen Mitteln der gymnasialen Mittelstufe, Landesbildungsserver Baden-Württemberg
- Episodes in Nineteenth and Twentieth Century Euclidean Geometry von Ross Honsberger (englisch) S. 34 ff - auch als pdf oder epub.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Wolfgang Zeuge: Nützliche und schöne Geometrie - Eine etwas andere Einführung in die Euklidische Geometrie. Zweite korrigierte und ergänzte Auflage, Springer Spektrum, Springer-Verlag GmbH, Berlin 2021, ISBN 978-3-662-63830-9, Seiten 120 und 121.
- ↑ Ross Honsberger: Gitter - Reste - Würfel Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig 1984, ISBN 978-3-528-08476-9, Seiten 218 und 219
- ↑ George Zerr: Problem 90, American Mathematical Monthly, 1898, S. 143
- ↑ Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten - Perlen der klassischen Geometrie, 2. Auflage, Springer Spektrum 2016, ISBN 978-3-662-63329-8, S. 23/220
- ↑ Titu Andreescu, Oleg Mushkarov, Luchezar N. Stoyanov: Geometric Problems on Maxima and Minima. Birkhäuser, Boston u. a. 2006, ISBN 0-8176-3517-3, S. 69 (Auszug (Google)).
- ↑ Harald Schröer, Universitätsbibliothek Heidelberg: Die 4. Seite und der Flächeninhalt des Sehnenvierecks
- ↑ C. V. Durell, A. Robson: Advanced Trigonometry
- ↑ Wolfgang Zeuge: Nützliche und schöne Geometrie - Eine etwas andere Einführung in die Euklidische Geometrie. Zweite korrigierte und ergänzte Auflage, Springer Spektrum, Springer-Verlag GmbH, Berlin 2021, ISBN 978-3-662-63830-9, S. 133–134.


























































































