Stereografische Projektion
Eine stereografische Projektion (auch konforme azimutale Projektion) ist eine Abbildung einer Kugelfläche in eine Ebene mit Hilfe einer Zentralprojektion, deren Projektionszentrum (PZ) auf der Kugel liegt. Die das Projektionszentrum und den Kugelmittelpunkt enthaltende Gerade ist orthogonal zur Bildebene, die traditionell die dem Projektionszentrum gegenüberliegende Tangentialebene ist.[1]
Die stereografische Projektion wurde zuerst bei der Abbildung der Himmelskugel auf dem Astrolabium angewendet. Entdeckt wurde sie bereits in der Antike, vermutlich von Hipparchos um 130 v. Chr. Ausführlich und mit geometrischem Beweis dafür, dass Kreise der Kugeloberfläche in Kreise der Bildebene übergehen (Kreistreue), ist sie in der kleinen Abhandlung Planisphaerium des Ptolemäos (ca. 85–160) dargelegt. Die Idee, die Kreis- und die Winkeltreue dieser Abbildung auch für kartografische Abbildungen der Erdoberfläche zu nutzen, hatte erstmals der Nürnberger Astronom und Mathematiker Johannes Werner (1468–1528).[1] Sie hat allerdings den Nachteil merklicher Flächenverzerrungen an den Kartenrändern.
In der Kristallografie findet die stereografische Projektion praktische Anwendung in der Darstellung der Gitterebenen eines Kristalls (üblicherweise winkeltreu mittels des sogenannten Wulff’schen Netzes)[2] und in der Strukturgeologie bei der Darstellung von Geländedaten wie des Streichens und Fallens von Schicht-, Schieferungs-, Verwerfungs- und Kluftflächen (üblicherweise flächentreu mittels des sogenannten Schmidt’schen Netzes).[3]
In der reinen Mathematik hat die stereografische Projektion eine erweiterte, abstraktere Bedeutung. Sie wird auch für höherdimensionale Räume, also nicht nur zur Abbildung aus dem dreidimensionalen in den zweidimensionalen Raum, benutzt.[4][5]

Anwendungsbeispiele[Bearbeiten | Quelltext bearbeiten]




Astrolabium und Sternkarte[Bearbeiten | Quelltext bearbeiten]
Das Astrolabium in Bild 1 enthält den nördlichen Himmel. Die projizierten Sterne (inklusive Tierkreis) befinden sich auf der um das Bild des nördlichen Himmelspols (Polarstern) drehbaren Rete. Auf der festen Unterlage (Tympanon) ist die sogenannte Safiha eingraviert, die aus den Abbildern der zum Zenit konzentrischen, horizontparallelen Höhenkreise (Almukantarate), des Horizonts (Abbild: eine konkave Linie) und der dazu rechtwinkligen Azimutkreise besteht.
Eine der in Bild 2 abgebildeten drehbaren Planisphere ähnliche Sternkarte ist das prinzipiell gleich funktionierende und nützliche, aber preiswertere Folgeprodukt des Astrolabiums.[6] Der unterbrochene Kreisbogen ist die Ekliptik, ein Stück eines in der Abbildung zum Polbild exzentrischen Kreises.
Kartografie der Erdoberfläche[Bearbeiten | Quelltext bearbeiten]
Die leichte zeichnerische Herstellbarkeit (nur Kreise und Geraden für Kreise auf der Erdoberfläche) und die Winkeltreue wurden bereits im Altertum auch für Karten und für die Navigation genutzt. Wird der Berührungspunkt der Abbildungsebene zum Beispiel in eine Hafenstadt gelegt, so sind die kürzesten Wege zu Zielen in allen Richtungen als Geraden abgebildet.
Bei der polaren stereografischen Projektion (der Berührpunkt der Abbildungsebene liegt im Nord- oder Südpol) werden die Meridiane des geografischen Koordinatensystems der Erde als Geraden durch den Erdpol abgebildet (siehe Bild 3). Die Navigationselemente geografische Länge und geografische Breite werden daher durch diese Projektionsart für Navigationszwecke an den Polen anschaulich wiedergegeben. Die Abbildung der Polarregionen als Teile der modernen internationalen Weltkarte erfolgt ebenfalls über die stereografische Projektion.
In der Geophysik werden Karten über die Verteilung von Kräften oder Linienstrukturen auf der Erdkugel auf einem stereografischen Netzentwurf aufgebaut.
Mathematische Behandlung[Bearbeiten | Quelltext bearbeiten]
Umrechnung Bild- in Objektkoordinaten[Bearbeiten | Quelltext bearbeiten]

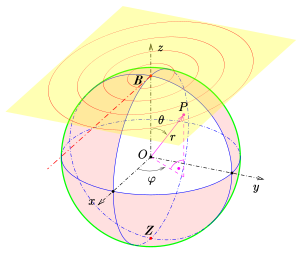
Für die Objektpunkte werden sphärische (, wie in Abbildung 2) und für die Bildpunkte ebene Polarkoordinaten (Radius , Richtung , wie in Abbildung 3) verwendet.
Ein Objektpunkt wird auf den Bildpunkt abgebildet.
Für die Winkel und wird die gleiche Bezugsrichtung angenommen. Somit gilt:
Der Abstand (radiale Polarkoordinate) wird aus Dreiecksbetrachtungen (siehe Abbildung 3) ersichtlich:
Während die Länge des Bogens auf der Kugel vom Berührungspunkt zum Breitenkreis linear zunimmt, vergrößert sich der Radius in der Ebene progressiv bis ins Unendliche (bis zum Projektionszentrum). Diese sogenannte Längenverzerrung ist der Differentialquotient der auf normierten Funktion nach :
Wegen des stark progressiven Wachsens der Verzerrung (unendlich groß bei ) bleiben die stereografischen Abbildungen in der Praxis auf beschränkt.
|
|
|
Geografische Koordinaten der Erde[Bearbeiten | Quelltext bearbeiten]
Will man die nördliche Halbkugel stereografisch abbilden, so ergeben sich die Zuordnungen:
- Das Projektionszentrum fällt mit dem Südpol zusammen, der Berührungspunkt mit dem Nordpol.
Auf diese Weise erscheinen die Breitengrade in der Projektionsebene als konzentrische Kreise um den Berührungspunkt (= Nordpol) und die Längengrade als Ursprungshalbgeraden.
Für die südliche Halbkugel gilt:
- Das Projektionszentrum fällt mit dem Nordpol zusammen, der Berührungspunkt mit dem Südpol.
Geometrie ebener Kurven[Bearbeiten | Quelltext bearbeiten]
Gegeben sei eine beliebige Kurve in der Ebene in expliziter Polarkoordinatendarstellung. Nun lege man die Projektionskugel mit Radius auf den Koordinatenursprung, den Tangentialpunkt TP. Durch das Projektionszentrum – den auf der Kugeloberfläche gegenüberliegenden Punkt PZ – legt man nun eine zweite Ebene, die parallel zur ursprünglichen Ebene liegt (also durch Parallelverschiebung der ersten Ebene senkrecht zu selbiger um entsteht). Nun werde mittels stereografischer Projektion in PZ die gegebene Kurve in der ersten Ebene auf die Sphäre projiziert. Indem der ursprüngliche Punkt TP als neues Projektionszentrum genutzt wird, wird durch eine weitere stereografische Projektion die Kurve auf der Sphäre auf die zweite Ebene projiziert – sie sei dort in Polarkoordinaten durch beschrieben. Dann gilt . Die gegebene Kurve ist also durch diese doppelte stereografische Projektion am Kreis mit Radius in der (parallelen) Bildebene invertiert worden.
Kreistreue[Bearbeiten | Quelltext bearbeiten]
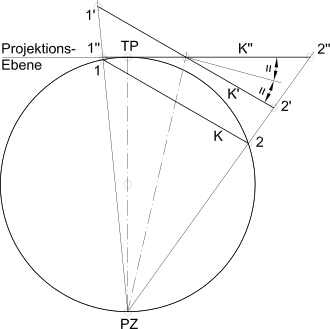
Die Strahlen aus dem Projektionszentrum PZ (Abb.) an den Urkreis K (Durchmesserpunkte 1 und 2) bilden einen schiefen Kreiskegel, dessen zu K paralleler Schnitt K’ kreisförmig ist. Die Projektionsebene K’’ schneidet die Kegelachse gleich schräg wie der Schnitt K’, weshalb die in ihr liegende Schnittfigur ebenfalls ein Kreis (Punkte 1’’ und 2’’) ist.
Wichtig: Die Kreistreue gilt generell nur für die Kreislinie. Der Mittelpunkt des Objektkreises wird z. B. nicht als Mittelpunkt des Bildkreises abgebildet. Hiervon sind nur die Fälle, bei denen der Kreiskegel gerade ist, ausgenommen.
Weitere Besonderheiten der stereografischen Projektion sind:
- Das Bild des Projektionszentrums liegt im Unendlichen.
- Alle Kreise auf der Kugeloberfläche werden als Kreise abgebildet (Kreistreue).
- Kreise durch das Projektionszentrum werden als Geraden dargestellt.
Kugelspiegelung (Inversion)[Bearbeiten | Quelltext bearbeiten]
Eine stereografische Projektion lässt sich auch als Spiegelung an einer Kugel (Inversion) interpretieren. Aus den Eigenschaften einer Inversion folgen dann sofort die Kreistreue und Winkeltreue.
Verallgemeinerung auf ℝn[Bearbeiten | Quelltext bearbeiten]
Die oben beschriebene Projektion ist der Spezialfall der allgemeinen stereografischen Projektion: Im dreidimensionalen Raum wird die zweidimensionale Kugeloberfläche auf die Kartenebene und somit in den zweidimensionalen Raum abgebildet. Die allgemeine Abbildung sieht wie folgt aus:
Es ist jedoch auch möglich, das Urbild dieser Funktion so zu wählen, dass sein Äquator die Projektions-Hyperebene schneidet:

Diese Abbildung ist für den Punkt , den sogenannten Nordpol, natürlich nicht definiert. Betrachtet man die Abbildung , deren Funktionsterm statt im Nenner hat, dann wird die Sphäre bis auf den Südpol abgebildet.
Ändert man das Urbild der stereografischen Projektion auf diese Weise, so erhält man durch die beiden Abbildungen und einen Atlas der n-Sphäre.
Herleitung[Bearbeiten | Quelltext bearbeiten]
Exemplarisch wird hier die stereografische Projektion durch den Nordpol hergeleitet. Für die Projektion durch den Südpol kann die gleiche Herleitung verwendet werden. Die stereografische Projektion durch den Nordpol soll einen Punkt der Sphäre auf seinen Bildpunkt in der Hyperebene so abbilden, dass der Bildpunkt auf der Geraden durch den Nordpol und liegt.
Diese Gerade kann durch
parametrisiert werden. Diese Gerade schneidet die Ebene , wobei gilt:
Daraus folgt, dass die Koordinaten des Schnittpunktes von und durch
gegeben sind. Betrachtet man nun die Ebene als , so erhält man die stereografische Projektion durch den Nordpol.
Umkehrfunktionen[Bearbeiten | Quelltext bearbeiten]
Zu den stereografischen Projektionen durch Nord- bzw. Südpol existieren die durch
beschriebenen stetigen Umkehrfunktionen. Daher sind und Homöomorphismen. Man hat mit der Projektion aus dem Nordpol und der aus dem Südpol einen möglichen Atlas gefunden. Damit ist gezeigt, dass die -Sphäre eine -dimensionale topologische Mannigfaltigkeit ist.
Kreistreue[Bearbeiten | Quelltext bearbeiten]
Sei eine Hyperebene in . Ist und , so folgt aus der Ebenengleichung von sowie der Cauchy-Schwarzschen Ungleichung:
Das Bild der Punkte der Ebene durch erfüllt die Gleichung:[7]
Dies ist eine Sphärengleichung. Daher bildet alle Schnitte von und einer beliebigen Hyperebene, also insbes. Sphären, die in dieser Hyperebene liegen, auf Sphären in ab.
Kompaktifizierung der komplexen Zahlenebene[Bearbeiten | Quelltext bearbeiten]
Die stereografische Projektion kann unter anderem zur Kompaktifizierung der komplexen Zahlenebene herangezogen werden. Man erweitert um einen zusätzlichen Punkt, der hier mit bezeichnet wird. Die Menge heißt Einpunktkompaktifizierung von oder Riemannsche Zahlenkugel.
Die Abbildung wird mittels der Abbildung
fortgesetzt. Man nennt nun offen genau dann, wenn offen in ist. Dadurch wird auf eine Topologie induziert.
Chordale Metrik[Bearbeiten | Quelltext bearbeiten]
Dieselbe Topologie wird durch die durch
definierte chordale Metrik induziert.
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Literatur[Bearbeiten | Quelltext bearbeiten]
Quellen für die mathematischen Erläuterungen:
- Konrad Königsberger: Analysis. Band 2. Springer-Verlag, Berlin u. a. 1993, ISBN 3-540-54723-1.
- Allgemeine Beschreibung n-dim. Sphäre: Abschnitt 1.3.II, Konformität: Abschnitt 3.1.
- Günter Scheja, Uwe Storch: Lehrbuch der Algebra. Band 1. 2. überarbeitete und erweiterte Auflage. Teubner, Stuttgart 1994, ISBN 3-519-12203-0.
- Projektive Darstellung: Abschnitt V.H Bsp. 4.
- Günther Bollman, Günther Koch (Hrsg.): Lexikon der Kartographie und Geomatik. Band 1: A bis Karti. Spektrum Akademischer Verlag, Heidelberg u. a. 2001, ISBN 3-8274-1055-X.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Animierte Erklärung der stereografischen Projektion (deutsch)
- Interaktive dreidimensionale Darstellung der stereografischen Projektion (englisch; Java-Applet)
- Vergleich verschiedener Projektionen (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b Mathematik.de: Kreisverwandte Abbildungen.
- ↑ Guido Schmitz: Materialphysik I. Vorlesungsskript. Uni Münster, 2012, S. 2 f.
- ↑ Jean-Pierre Burg: Strukturgeologie: Strukturelle Analyse der Polyphasen Defromation. Vorlesungsskript (Kapitel 10), ETH Zürich, 2017, S. 287 ff.
- ↑ Elena Perk: Stereographische Projektion. ( vom 11. Januar 2016 im Internet Archive) S. 2.
- ↑ Karlhorst Meyer: Stereographische Projektion. S. 12.
- ↑ Ein prinzipieller Unterschied ist die Spiegelverkehrtheit des Himmelsbildes auf dem Astrolabium, denn die antiken Astronomen bevorzugten die Sicht von außen auf die Himmelskugel.
- ↑ Hierbei darf man durch teilen. Denn wenn dies gleich 0 wäre, läge der Nordpol in der Ebene.