Kreisspiegelung

Punkt P am Kreis gespiegelt ergibt P'

Die Spiegelung am Kreis oder Kreisspiegelung ist eine Abbildung der ebenen Geometrie, die das Innere und das Äußere eines gegebenen Kreises miteinander vertauscht.

Die Abbildung ist winkeltreu und zählt zu den speziellen konformen Transformationen.

Eine Kreisspiegelung ist der ebene Fall einer geometrischen Inversion. Eine Inversion im Raum ist die Spiegelung an einer Kugel, kurz Kugelspiegelung, mit ähnlichen Eigenschaften wie die der Kreisspiegelung.

Definition

Zur Definition der Spiegelung an einem Kreis, Punkt P und der gespiegelte Punkt P'

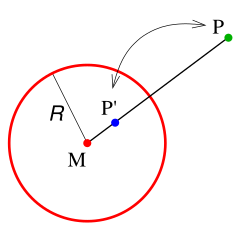
Für die Kreisspiegelung an einem Kreis mit Mittelpunkt $M$ und Radius $R$ ist der Bildpunkt $P'$ (siehe Bild) eines Punktes $P$ dadurch festgelegt, dass $P'$ auf einer Strecke $|{\overline {MP}}|$ bzw. auf einer Halbgeraden $[MP$ liegen und die Bedingung

$|{\overline {MP'}}|={\frac {R^{2}}{|{\overline {MP}}|}}$

erfüllen muss. Dabei darf der ursprüngliche Punkt $P$ nicht mit dem Mittelpunkt $M$ übereinstimmen. Gelegentlich umgeht man dieses Problem, indem man einen neuen Punkt zur Ebene hinzufügt und diesen als Bildpunkt von $M$ definiert. Der Bildpunkt dieses neuen Punktes ist der Mittelpunkt des Inversionskreises. Dieser wird auch Inversionszentrum und der Radius Inversionsradius genannt, was auch im Folgenden geschieht.

Analytische Beschreibung

Ist in der xy-Ebene das Inversionszentrum $M$ bei $(x_{0},y_{0})$, so lautet der Bildpunkt des Punktes mit Koordinaten $(x,y)\neq (x_{0},y_{0})$:

$(x',y')=(x_{0},y_{0})+{\frac {R^{2}(x-x_{0},y-y_{0})}{(x-x_{0})^{2}+(y-y_{0})^{2}}}$

In ebenen Polarkoordinaten $r,\varphi$ besitzt eine Kreisspiegelung eine besonders einfache Darstellung:

$(r,\varphi )\rightarrow \left({\frac {R^{2}}{r}},\varphi \right)$.

Die Spiegelung am Einheitskreis ist dann

$(r,\varphi )\rightarrow \left({\frac {1}{r}},\varphi \right)$

und rechtfertigt die Bezeichnung Inversion.

In der Funktionentheorie behandelt man die Inversionen und die von ihnen erzeugten Kreisverwandtschaften am besten in der komplexen („Gaußschen“) Zahlenebene. Eine Inversion am Einheitskreis wird dabei durch die Abbildung $z\mapsto {\frac {1}{\overline {z}}}$ beschrieben. Darin bezeichnet $z$ eine komplexe Zahl und ${\overline {z}}$ die zugehörige konjugiert komplexe Zahl.

Eigenschaften

• Die Abbildung vertauscht Inneres und Äußeres des Inversionskreises, die Punkte auf seinem Umfang sind Fixpunkte.

• Wendet man die Inversion zweimal an, so erhält man wieder die Ausgangssituation, die Inversion ist also eine Involution.

• Die Inversion ist eine konforme Abbildung, d. h., sie ist winkeltreu. Insbesondere werden Objekte, die einander berühren, auch wieder auf solche abgebildet.

• Die Inversion kehrt wie die Geradenspiegelung die Orientierung um.

• Die Verknüpfung zweier Inversionen um konzentrische Kreise ist eine Zentrische Streckung und behält die Orientierung.

• Im Gegensatz zur Punkt-, Achsen- oder Ebenenspiegelung die ist Inversion keine Kongruenzabbildung.

• Geraden, die nicht durch den Mittelpunkt des Inversionskreises verlaufen, werden auf Kreise abgebildet, die durch den Mittelpunkt gehen.

• Geraden, die durch den Mittelpunkt des Inversionskreises verlaufen, werden auf sich selbst abgebildet.

• Kreise, die durch den Mittelpunkt des Inversionskreises verlaufen, werden auf Geraden abgebildet, die nicht durch den Mittelpunkt gehen.

• Kreise, die nicht durch den Mittelpunkt des Inversionskreises verlaufen, werden wieder auf solche Kreise abgebildet. Allerdings wird der Mittelpunkt des ursprünglichen Kreises durch die Inversion nicht auf den Mittelpunkt des Bildkreises abgebildet.

• Kreise, die den Inversionskreis rechtwinklig schneiden, werden auf sich selbst abgebildet.

• Hat ein Punkt den doppelten (q-fachen) Abstand vom Inversionszentrum wie ein anderer Punkt, dann hat er nach der Spiegelung den halben (1/q-fachen) Abstand vom Inversionszentrum wie der andere Punkt.

• Wenn P ein Punkt ist, der nicht auf dem Inversionskreis liegt, P' sein Spiegelbild und A und B die Schnittpunkte der Geraden PP' mit dem Inversionskreis sind, dann bilden P,A,P',B eine harmonische Teilung.

• Wenn M das Inversionszentrum, R der Inversionsradius, A' das Spiegelbild des Punktes A und B' das Spiegelbild des Punktes B ist, dann sind die Dreiecke ΔMAB und ΔMB'A' spiegelbildlich ähnlich und einander entsprechende Seiten sind um den Faktor ${\mathsf {\tfrac {R^{2}}{|MA|\cdot |MB|}}}$ gestreckt. Insbesondere ist ∠MAB=∠A'B'M.

Spezielle Abbildungen

In diesem Abschnitt werden die Abbildungen von Punkten, Kreisen und Geraden vorgestellt, und das jeweils in analytischer Beschreibung, Konstruktion mit Zirkel und Lineal und Konstruktion mit Zirkel allein. Bei letzteren Konstruktionen gilt nach Mascheroni:

„Das einzige Zeichenhilfsmittel, welches in diesem Abschnitte gebraucht werden darf, ist der Zirkel; nur das Schlagen von Kreisbogen ist erlaubt; es darf in der Konstruktion nicht eine einzige gerade Linie gezeichnet werden.“

Die gelegentlich in den Abbildungen eingezeichneten gestrichelten bzw. gepunkteten Linien haben keine konstruktive Funktion; sie dienen dort lediglich der Verdeutlichung und dem Beweis.

Kreisspiegelung eines Punktes

Analytische Beschreibung

Liegt das Inversionszentrum bei $(x_{0},y_{0})$ und ist der Inversionsradius $R$, dann liegt der Bildpunkt von $(x,y)$ wie in der #Definition bereits angegeben bei

$(x',y')=(x_{0},y_{0})+{\frac {R^{2}(x-x_{0},y-y_{0})}{(x-x_{0})^{2}+(y-y_{0})^{2}}}$

In der komplexen („Gaußschen“) Zahlenebene hat die Spiegelung am Kreis um das Inversionszentrum $c$ mit Inversionsradius $R$ die Darstellung:

$z'=c+{\frac {R^{2}}{\overline {z-c}}}$

In ihrer Polarform $z=r{\rm {e}}^{{\rm {i}}\varphi }$ mit komplexem Argument $\varphi$ schreibt sich das ähnlich wie in Polarkoordinaten oben:

$z=c+r{\rm {e}}^{{\rm {i}}\varphi }\mapsto c+{\frac {R^{2}}{r}}{\rm {e}}^{{\rm {i}}\varphi },\;r\neq 0$

Konstruktion mit Zirkel und Lineal

Bild 1: Konstruktionen des am Inversionskreis (rot) gespiegelten Punktes P bzw. P' mit Zirkel und Lineal.

Liegt P auf dem Inversionskreis, so ist P' gleich P. Für den anderen Fall zeigen Bilder 1 und 2 bekannte Konstruktionen mit Zirkel und Lineal oder Lineal allein des gespiegelten Bildpunktes P'.

Konstruktion mit einem Kreis beliebigen Radius' (grün im Bild 1)

Bei dieser Konstruktion wird um P ein Kreis geschlagen, der den Inversionskreis in zwei Punkten A und B schneidet. Die Gerade PA schneidet den Inversionskreis ein zweites Mal in C und die Linie von B nach C schneidet MP in P'. Die Gültigkeit dieser Konstruktion folgt aus dem Kreiswinkelsatz und der harmonischen Teilung der Strecke PE durch die Winkelhalbierende des Dreiecks ΔPBP', die in der folgenden Konstruktion mit Winkelhalbierenden (lila im Bild 1, siehe unten) direkt ausgenutzt wird.

Die Konstruktion mit der Tangente an den Inversionskreis durch P (blau im Bild 1, siehe unten) ist der Spezialfall A=C, und ein weiterer sinnfälliger Spezialfall ist, wenn AB Durchmesser des Inversionskreises ist, siehe #Stereografische Projektion und Kreisspiegelung.

Konstruktion mit Winkelhalbierenden (lila im Bild 1)

Bei dieser Konstruktion wird die Gerade DB durch den Punkt D, der auf der Gerade MP und dem Inversionskreis nahe P liegt, und einen beliebigen Punkt B auf dem Inversionskreis gezogen. Der Bildpunkt P' ergibt sich durch Geradenspiegelung von PB an DB und Ermittlung des Schnittpunkts der Bildgeraden mit MP. Der Beweis, dass man so den Bildpunkt erhält, folgt aus der harmonischen Teilung der Strecke PE durch die Winkelhalbierende des Dreiecks ΔP'PB:

(MP-R):(R-MP')=(MP+R):(MP'+R)

was äquivalent ist zu MP=R²/MP'.

Konstruktion mit der Tangente an den Inversionskreis durch P (blau im Bild 1)

Falls der Punkt P außerhalb des Kreises liegt (Bild 1), zeichnet man mithilfe des Thaleskreises die beiden Kreistangenten durch P. Anschließend bringt man die Verbindungsstrecke der beiden Berührpunkte mit der Halbgeraden [MP zum Schnitt. Der Schnittpunkt ist der gesuchte Bildpunkt P'.

Liegt der Punkt P dagegen im Kreisinneren, so beginnt man mit der zur Halbgeraden [MP senkrechten Kreissehne durch P und konstruiert die beiden Kreistangenten in den Endpunkten dieser Sehne. P' ergibt sich dann als Schnittpunkt dieser Tangenten.

Der Beweis, dass man so den Bildpunkt erhält, folgt direkt aus dem Kathetensatz.

Bild 2: Konstruktionen des am Inversionskreis (rot) gespiegelten Bildpunktes P' mit Zirkel und Lineal.

Konstruktion mit Kreis durch M (orange im Bild 2)

Bei dieser Konstruktion wird der Kreis um den Punkt P durch M mit dem Inversionskreis zum Schnitt gebracht, und der Kreis um den Schnittpunkt N durch M schneidet MP ein zweites Mal in P', was aus der Ähnlichkeit der Dreiecke ΔPNM und ΔNMP' folgt.

Konstruktion nur mit Lineal und dem Inversionskreis (blau im Bild 2)

Bei dieser Konstruktion muss der zu spiegelnde Punkt P' im Inversionskreis liegen. Zunächst werden die Punkte A und B markiert, in denen die Gerade MPP' den Inversionskreis schneidet. Es wird eine beliebige Gerade durch den zu spiegelnden Punkt P' gezeichnet und mit dem Inversionskreis zum Schnitt gebracht, die Punkte C und D ergebend. Die Gerade AC schneidet BD in E und die Gerade BC schneidet AD in F. Der Bildpunkt P von P' ist der Schnittpunkt der Verbindung EF mit MP'.

Liegt der zu spiegelnde Punkt P hingegen außerhalb des Inversionskreises, wird zunächst die Senkrechte zu [MP in P errichtet und ein beliebiger Punkt E auf ihr markiert. Die Gerade AE schneidet den Inversionskreis in C, die Gerade EB schneidet den Inversionskreis in D, und CD liefert im Schnittpunkt mit MP das Spiegelbild P'.

Konstruktion nur mit Lineal (grün im Bild 2)

Hier wird ein beliebiger Punkt G und ein beliebiger Punkt H auf der Strecke BG gewählt, wobei B der P nahe Schnittpunkt des Inversionskreises mit MP ist, und A ist der P ferne Schnittpunkt. Die Gerade PH schneidet GA in I und IB schneidet AH in J. Der Bildpunkt P' ist der Schnittpunkt der Geraden GJ mit MP.

Konstruktion mit Zirkel allein

Bild 3: Der Urbildpunkt $P$ wird nur mit Hilfe eines Zirkels am Inversionskreis (rot) gespiegelt, es ergibt sich der Bildpunkt $P'.$

• Liegt der Punkt $P$ außerhalb des Inversionskreises (Bild 3), so zeichnet man um $P$ einen Kreis durch den Mittelpunkt des Inversionskreises. Dieser schneidet den Inversionskreis in zwei Punkten. Zeichne auch um diese Punkte Kreise durch den Mittelpunkt. Diese beiden Kreise schneiden sich nun im Bildpunkt $P'$.
• Liegt $P$ auf dem Inversionskreis, so ist keine Konstruktion notwendig, es gilt $P'=P.$
• Liegt $P$ innerhalb des Inversionskreises, kann z. B. mithilfe einer Einteilung der möglichen Lagen des Punktes $P$ in drei Bereiche (Bild 4–6), eine deutliche Vereinfachung des Konstruktionsaufwandes für zwei Bereiche erreicht werden. Hierfür stellt man sich, quasi gedanklich, eine Kreisfläche (hellgrau) vor, deren Radius gleich ist dem halben Radius des Inversionskreises. Für die eigentliche Konstruktion ist die Kreisfläche (hellgrau) nicht erforderlich. Die drei Bereiche der möglichen Lage des Punktes $P$, meist gegeben als Abstand zum Mittelpunkt $M$ des Inverskreises, und die dafür möglichen Konstruktionsmethoden sind:

1. Der Abstand des Punktes $P$ zu $M$ (Bild 4) ist größer als der halbe Radius des Inversionskreises, d. h. $|{\overline {MP}}|>{\frac {1}{2}}R.$

Zuerst wird um den Punkt $P$ ein Kreis mit Radius $|{\overline {MP}}|$ gezogen. Dieser schneidet den Inversionskreis in den Punkten $A$ und $B.$ Die abschließenden Kreise um $A$ und $B$ mit den Radien $|{\overline {AM}}|$ bzw. $|{\overline {BM}}|$ liefern den Bildpunkt $P'.$

2. Der Abstand des Punktes $P$ zu $M$ (Bild 5) ist gleich dem halben Radius des Inversionskreises, d. h. $|{\overline {MP}}|={\frac {1}{2}}R.$ Hierzu wird der Radius $|{\overline {MP}}|$ mit $4$ multipliziert um den Bildpunkt $P'$ zu erhalten.

Zuerst wird um den Punkt $P$ ein Kreis mit Radius $|{\overline {MP}}|$ gezogen und anschließend, mittels dreimaligem Abtragen dieses Radius ab dem Punkt $M$, sein Durchmesser $|{\overline {MC}}|$ bestimmt. Als Nächstes wird der letzte Kreis mit dem Radius $|{\overline {MC}}|$ um den Punkt $C$ gezogen. Abschließend bedarf es noch eines zweimaligen Abtragens dieses Radius, ab den soeben erzeugten Schnittpunkt $D,$ um den Bildpunkt $P'$ zu erhalten.

Bild 6: Der Abstand des Punktes $P$ zu $M$ ist kleiner als die Hälfte, aber größer als ein Achtel des Radius des Inversionskreises (rot), ${\tfrac {1}{8}}R<|{\overline {MP}}|<{\tfrac {1}{2}}R.$, $|{\overline {MP'}}|=6\cdot |{\overline {MP}}|$

Bild 5: Der Abstand des Punktes $P$ zu $M$ ist gleich dem halben Radius des Inversionskreises (rot),  $|{\overline {MP}}|={\tfrac {1}{2}}R.$, $|{\overline {MP'}}|=4\cdot |{\overline {MP}}|$

Bild 4: Der Abstand des Punktes $P$ zu $M$ ist größer als der halbe Radius des Inversionskreises (rot), $|{\overline {MP}}|>{\tfrac {1}{2}}R.$

3. Der Abstand des Punktes $P$ zu $M$ (Bild 6) ist kleiner als die Hälfte, aber größer als ein Achtel des Radius des Inversionskreises, d. h. ${\frac {1}{8}}R<|{\overline {MP}}|<{\frac {1}{2}}R.$ Hierzu wird der Radius $|{\overline {MP}}|$ mit $6$ multipliziert um den Bildpunkt $P'$ zu erhalten.

Im nebenstehenden Bild 6, veranschaulicht die kleine Kreisfläche (rosa) ein Achtel des Radius des Inversionskreises. Für die eigentliche Konstruktion ist die Kreisfläche (rosa) nicht erforderlich. Dies gilt ebenso für die eingezeichneten gepunkteten Linien; sie sollen lediglich einen Vergleich mit der Konstruktion Mit Zirkel und Lineal verdeutlichen.

Zuerst wird um den Punkt $P$ ein Kreis mit Radius $|{\overline {MP}}|$ gezogen und anschließend, durch ein dreimaliges Abtragen dieses Radius, sein Durchmesser $|{\overline {MC}}|$ bestimmt. Es folgt ein Kreisbogen um $C$ mit Radius $|{\overline {MC}}|,$ auf dem, analog zuvor, der Durchmesser $|{\overline {MF}}|$ erzeugt wird. Nun wird ein Kreisbogen um $F$ mit Radius $|{\overline {MF}}|$ gezogen, der den Inversionskreis in $G$ und $H$ schneidet. Je ein Kreisbogen um $G$ und $H$ mit den Radien $|{\overline {MG}}|$ bzw. $|{\overline {MH}}|$ schließen sich an und schneiden sich in $I.$ Um $I$ wird ein Kreisbogen mit Radius $|{\overline {MI}}|$ gezogen auf dem, analog zuvor, der Durchmesser $|{\overline {ML}}|$ erzeugt wird. Als Nächstes wird der letzte Kreis mit dem Radius ${\overline {ML}}$ um den Punkt $L$ gezogen. Abschließend bedarf es noch eines dreimaligen Abtragens dieses Radius, ab dem Punkt $M$ um den Bildpunkt $P'$ zu erhalten.

• Universelle Methode für Liegt $P$ innerhalb des Inversionskreises:

Zunächst halbiert man den Radius des Inversionskreises so oft, bis man einen neuen Kreis erhält, der den Punkt $P$ nicht mehr enthält. (Dies ist mit Zirkel allein möglich.) Anschließend konstruiert man wie oben (Bild 4) den Bildpunkt von $P$, wobei die Inversion am neuen Kreis durchgeführt wird. Zuletzt verdoppelt man den Abstand des Bildpunktes doppelt so oft wie man den Radius halbiert hat. (Auch dies ist mit Zirkel allein möglich.) Dieser Punkt ist der gesuchte Bildpunkt.

Auf Grund der Komplexität dieses Verfahrens wird man die Konstruktion wohl kaum durchführen, sie bietet aber eine Möglichkeit den Satz von Mohr-Mascheroni zu beweisen, der besagt, dass man mit Zirkel allein alle Konstruktionen durchführen kann, die mit Zirkel und Lineal möglich sind.

Kreisspiegelung einer Geraden

Bei der Kreisspiegelung von Geraden sind zwei Fälle zu unterscheiden:

1. Geraden, die durch das Inversionszentrum führen, werden auf sich selbst abgebildet.
2. Andere Geraden werden auf Kreise abgebildet, die durch das Inversionszentrum führen und dort eine Tangente besitzen, die parallel zur Geraden ist. Der Mittelpunkt des Kreises liegt auf der Strecke vom Inversionszentrum zu dessen Fußpunkt auf der Geraden.

Analytische Beschreibung

Der Fußpunkt des Inversionszentrums M auf der Geraden wird auf den Endpunkt des Durchmessers des Spiegelbildes abgebildet, der durch M verläuft. Daher stehen Durchmesser $d=|MD|$ des Kreises und Abstand $L=|MD'|$ des Fußpunkts D' vom Inversionszentrum auf der Geraden im Zusammenhang

$d={\frac {R^{2}}{L}}$

und können auseinander abgeleitet werden (blau im Bild 7). Mit dem Durchmesser kann der Kreis und mit dem Fußpunkt die Gerade angegeben werden; sie ist senkrecht auf $MD'$.

Konstruktion mit Zirkel und Lineal

Bild 7: Konstruktion der Kreisspiegelung von Geraden

Ist der Kreis gegeben und schneidet den Inversionskreis in zwei Punkten, so wie der grüne Kreis in den Punkten A und B im Bild 7, dann ist sein Spiegelbild die Gerade AB. Berührt der Kreis den Inversionskreis nur, so ist sein Spiegelbild die Tangente an den Inversionskreis in diesem Berührungspunkt (blassgelb). Wenn der Kreis keinen gemeinsamen Punkt mit dem Inversionskreis teilt, wie der blaue Kreis um N im Bild, dann wird, wie in #Kreisspiegelung eines Punktes beschrieben, das Spiegelbild des dem Inversionszentrum gegenüberliedenden Endes des Durchmessers D konstruiert. Im Bildpunkt D' wird die zu MD senkrechte Gerade errichtet, die das Spiegelbild des Kreises ist.

Ist die Gerade gegeben und schneidet sie den Inversionskreis in zwei Punkten, wie die grüne in den Punkten A und B, dann ist das Spiegelbild der Umkreis des Dreiecks mit Ecken in diesen beiden Punkten und Inversionszentrum M (grüner Kreis um P). Sein Mittelpunkt kann daher mit der Mittelsenkrechten JP der Strecke MB konstruiert werden. Bei Berührung der Gerade mit dem Inversionskreis ist das Spiegelbild der Thaleskreis über der Strecke vom Berührungspunkt zu M (blaßgelb.) Hat die Gerade keinen gemeinsamen Punkt mit dem Inversionskreis, wird zunächst der Fußpunkt des Inversionszentrums auf ihr konstruiert (D' im Bild). Dieser wird am Inversionskreis gespiegelt und liefert mit dem Inversionszentrum zwei Endpunkte des Durchmessers des Spiegelbildes, das sodann konstruiert werden kann. Weil der Mittelpunkt des Bildkreises den halben Abstand zum Inversionszentrum hat, wie der Endpunkt des Durchmessers, kann der Mittelpunkt als Bild des Punktes ermittelt werden, der den doppelten Abstand vom Inversionszentrum hat, wie der Fußpunkt. Im Bild hat N' den doppelten Abstand von M wie D' und somit liefert die Kreisspiegelung von N' direkt den Mittelpunkt N des Bildkreises.

Konstruktion mit Zirkel allein

Aufgabe

(Siehe hierzu Bild 8) Geraden, die nicht durch den Mittelpunkt des Inversionskreises verlaufen, werden auf Kreise abgebildet, die durch den Mittelpunkt gehen (siehe #Kreisspiegelung einer Geraden).

Die (imaginäre) Gerade $g$ (definiert durch die Punkte $A$ und $B$) ist am Inversionskreis $k$ zu spiegeln, um den Kreis $g'$ zu erhalten.

Bild 8: Spiegelung einer Geraden, die (imaginäre) Gerade $g$ (dunkelblau, definiert durch die Punkte $A$ und $B$) ist am Inversionskreis $k$ (rot) gespiegelt, um den Kreis $g'$ (hellgrün) zu erhalten.
Die gestrichelte Gerade ($g$) und die gepunktete Linie haben keine konstruktive Funktion, sie dienen lediglich der Veranschaulichung.
$|{\overline {OP}}|=|{\overline {PM'}}|$;    $|{\overline {OM}}|\cdot |{\overline {OM'}}|=|{\overline {OP}}|\cdot |{\overline {OP'}}|$

Animation Bild 8:
Spiegelung einer Geraden in 15 Bildern

1. Definieren der Geraden $g$:

Nach dem Einzeichnen des Inversionskreises $k$ um den Mittelpunkt $O$, mit beliebigem Radius, wird der Kreisbogens $b_{1}$ um $O$ ebenfalls mit beliebigem Radius gezogen. Die anschließend auf $b_{1}$ mit beliebiger Position festgelegten Punkte $A$ und $B$ definieren die Gerade $g$.

2. Bestimmen des Punktes $P$ (Mitte der Strecke ${\overline {AB}}$):

Die Punkte $C$ und $D$ werden bestimmt mittels Radius $|{\overline {AB}}|$ um $A$ und $B$, dies ermöglicht eine Gerade durch $C$ und $D$, sie steht senkrecht auf die Gerade $g$; Punkt $E$ entsteht mittels Radius $|{\overline {AB}}|$ um $B$ und Radius $|{\overline {DC}}|$ um $D$; die Punkte $F$ und $G$ werden bestimmt mittels Radius $|{\overline {EA}}|$ um $E$ und Radius $|{\overline {AB}}|$ um $A$; nach einem Kreisbogen mit Radius $|{\overline {GA}}|$ um $G$ und einem Kreisbogen mit gleicher Zirkelöffnung um $F$ ergibt sich der gesuchten Punkt $P$.

3. Der Mittelpunkt $O$ des Inversionskreises $k$ an der Geraden $g$ gespiegelt ergibt einen Punkt $M'$:

Die Punkte $H$ und $I$ werden auf dem Inversionskreis $k$ mittels Radius $|{\overline {PO}}|$ um $P$ bestimmt; Punkt $J$ erhält man mittels Radius $|{\overline {PO}}|$ um $P$ und $O$; Punkt $L$ ergibt sich mittels Radius $|{\overline {PO}}|$ um $P$ und $J$; je ein Kreisbogen mit Radius $|{\overline {PO}}|$ um $P$ und $L$ liefert den gesuchten Punkt $M'$.

4. Der Punkt $P$ am Inversionskreis $k$ gespiegelt ergibt einen Punkt $P'$ (Kreisspiegelung eines Punktes):

Die beiden Kreisbögen mit Radius $|{\overline {HO}}|$ um $H$ und $I$ liefern den gesuchten Punkt $P'$.

5. Dieser Punkt $M'$ am Inversionskreis $k$ gespiegelt ergibt den Mittelpunkt $M$ des Kreises $g'$ als Spiegelbild der Geraden $g$:

Der gezogene Kreisbogens $b_{2}$ um $M'$ mit Radius $|{\overline {M'O}}|$ liefert die Punkte $Q$ und $N$ auf dem Inversionskreis $k$. Nun bedarf es nur noch zweier Kreisbögen mit Radius $|{\overline {QO}}|$ um Punkt $Q$ und Punkt $N$, somit ist der gesuchte Mittelpunkt $M$ gefunden und der Kreis $g'$ kann abschließend mit dem Radius $|{\overline {MO}}|$ oder $|{\overline {MP'}}|$ gezogen werden.

In einer korrekten Konstruktion ergibt sich die Beziehung

$|{\overline {OM}}|\cdot |{\overline {OM'}}|=|{\overline {OP}}|\cdot |{\overline {OP'}}|$

Kreisspiegelung eines Kreises

Ein Kreis, der er durch das Inversionszentrum geht, wird auf eine Gerade abgebildet, siehe #Kreisspiegelung einer Geraden. An dieser Stelle werden Kreise betrachtet, die nicht durch das Inversionszentrum gehen. Deren Spiegelbilder sind Kreise. Allerdings sind die Mittelpunkte der Kreise nicht das Spiegelbild voneinander.

Analytische Beschreibung

Nach der Spiegelung eines Kreises mit Mittelpunkt $(x,y)$ und Radius $r$ hat dieser den Mittelpunkt und Radius:

$(x',y')=(x_{0},y_{0})+s(x-x_{0},y-y_{0}),\;r'=|s|r$   mit   $s={\frac {R^{2}}{(x-x_{0})^{2}+(y-y_{0})^{2}-r^{2}}}$

Im Nenner steht die Potenz des Inversionszentrums bezüglich des Kreises. Bei Kreisspiegelung in der komplexen Zahlenebene um das Inversionszentrum c liegt der Mittelpunkt des gespiegelten Kreises bei $c+s(z-c)$, wobei $s={\tfrac {R^{2}}{|z-c|^{2}-r^{2}}}$ ist. Der Radius $r'$ ist bereits oben angegeben.

Die Kreisspiegelung ist demnach eine zentrische Streckung um das Inversionszentrum c mit Streckfaktor |s|, und wenn s<0 erfolgt anschließend noch eine Drehung um 180°.

Konstruktion mit Zirkel und Lineal

Bild 9: Inversion von Kreisen

Bei der Konstruktion der Kreisspiegelung von Kreisen (schwarz in Bild 9 mit rotem Inversionskreis) wird eine beliebige, durch das Inversionszentrum M führende Sehne AB des Kreises gewählt und mit den im Abschnitt #Kreisspiegelung eines Punktes angegebenen Methoden das Spiegelbild A' von A konstruiert. Wegen der Konformität der Kreisspiegelung schließt die Tangente des Kreises in A und die seines Spiegelbilds in A' mit AB denselben Winkel ein. Somit kann der Mittelpunkt P des gespiegelten Kreises durch Verschiebung von NB nach A' und Verlängerung bis zur Geraden NM konstruiert werden. Diese Methode funktioniert auch, wenn der Kreis außerhalb des Inversionskreises liegt oder ihn schneidet.

Der Mittelpunkt P des Bildkreises kann durch Spiegelung des Inversionszentrums M am Kreis um N ermittelt werden, was zunächst den Bildpunkt M* ergibt (mittels des Linienzuges ABA"M*). Dieser Punkt ist das Spiegelbild P' des gesuchten Mittelpunkts P bezüglich des Inversionskreises um M. Der Punkt P entsteht im Bild aus dem Linienzug P'CC"D im Schnittpunkt der Geraden MN mit C"D.

Bei diesen Abbildungen der Kreise handelt es sich um zentrische Streckungen um M.

Konstruktion mit Zirkel allein

Aufgabe

(Siehe hierzu Bild 10)

Der Inversionskreis $a$ ist am Inversionskreis $k$ zu spiegeln, um den Kreis $a'$ zu erhalten.

Bild 10: Spiegelung eines Kreises, der Inversionskreis $a$ (dunkelblau) ist am Inversionskreis $k$ (rot) gespiegelt, um den Kreis $a'$ (hellgrün) zu erhalten.
Die gestrichelten Tangenten ($t_{1},\;t_{2},\;$dunkelblau) und die gepunkteten Linien haben keine konstruktive Funktion, sie dienen lediglich der Veranschaulichung.
$|{\overline {OM}}|\cdot |{\overline {OO'}}|=|{\overline {OQ}}|\cdot |{\overline {OQ'}}|=r^{2}$

Animation Bild 10:
Spiegelung eines Kreises in 16 Bildern

1. Konstruktion des Mittelpunktes des Inversionskreises $a$ und dessen (imaginären) Tangenten $t_{1}$ und $t_{2}$:

Nach dem Einzeichnen des Inversionskreises $k$ um den Mittelpunkt $O$ mit beliebigem Radius $r$ positioniert man den Punkt $A$ beliebig auf der Kreislinie, dies ermöglicht eine (imaginäre) Gerade durch $A$ und $O$. Der Radius $r$ ist auf der Kreislinie viermal abzutragen, Schnittpunkte sind $B,\;C,\;D$ und $E$. Es folgt der Kreisbogen mit Radius $r$ um Punkt $D$. Der Punkt $F$ ergibt sich mittels Radius $r$ um $C$; durch nochmaliges Abtragen des Radius $r$ um Punkt $F$ erhält man den Mittelpunkt $G$ des Inversionskreises $a$.

2. Der Mittelpunkt $O$ des Inversionskreises $k$ an dem Inversionskreises $a$ gespiegelt ergibt einen Punkt $O'$ (Kreisspiegelung eines Punktes):

Der eingezeichnete Inversionskreis $a$ erzeugt die Punkte $Q$ und $H$. Dies ermöglicht jetzt die beiden Tangenten (blau gestrichelte Linien) $t_{1}$ und $t_{2}$ des Kreises $a$ mit dem Scheitel $O$ und den Berührpunkten $Q$ und $H$ sowie die Gerade durch $Q$ und $H$, sie steht senkrecht auf die Gerade durch $A$ und $G$. Die Punkte $I$ und $J$ werden bestimmt mittels Radius $|{\overline {QH}}|$ um $Q$ und $H$; Punkt $K$ wird bestimmt mittels Radius $|{\overline {QH}}|$ um $H$ und Radius $|{\overline {IJ}}|$ um $I$; die Punkte $L$ und $N$ entstehen mittels Radius $|{\overline {QH}}|$ um $Q$ und Radius $|{\overline {KQ}}|$ um $K$; die beiden Kreisbögen mit Radius $|{\overline {LQ}}|$ um $L$ und $N$ liefern den gesuchten Punkt $O'$ (Mitte der Strecke ${\overline {QH}}$).

3. Dieser Punkt $O'$ am Inversionskreis $k$ gespiegelt ergibt den Mittelpunkt $M$ des Kreises $a'$ als Spiegelbild des Inversionskreises $a$:

Die Punkte $P$ und $R$ werden bestimmt mittels Radius $|{\overline {QO}}|$ um $Q$; die beiden Kreisbögen mit Radius $|{\overline {PO}}|$ um $P$ und $R$ liefern den Punkt $Q'$. Die beiden Punkte $S$ und $T$ erzeugt der Radius $|{\overline {O'O}}|$ um $O'$. Nun bedarf es nur noch zweier Kreisbögen mit Radius $|{\overline {SO}}|$ um Punkt $S$ und Punkt $T$. Somit ist der gesuchte Mittelpunkt $M$ gefunden und der Kreis $a'$ kann abschließend mit dem Radius $|{\overline {MQ'}}|$ gezogen werden.

In einer korrekten Konstruktion ergibt sich die Beziehung

$|{\overline {OM}}|\cdot |{\overline {OO'}}|=|{\overline {OQ}}|\cdot |{\overline {OQ'}}|=r^{2}$

Allgemeine Abbildungen

Ist eine Kurve in Parameterdarstellung

$t\in U\subseteq \mathbb {R} \mapsto (f(t),g(t))\in \mathbb {R} ^{2}$

gegeben, kann diese, wie in #Analytische Beschreibung erläutert, an einem Kreis gespiegelt werden:

$(x',y')=(x_{0},y_{0})+{\frac {R^{2}(f(t)-x_{0},g(t)-y_{0})}{(f(t)-x_{0})^{2}+(g(t)-y_{0})^{2}}}$

Das Resultat ist die zur gegebenen Kurve inverse Kurve. Die Tabelle enthält eine Auswahl an bekannten Kurven und ihrer inversen.

Kurve	Inverse Kurve
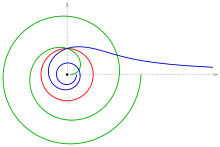
Logarithmische Spirale (grün), Archimedische Spirale (schwarz), Lituus-Spirale (blau),	Logarithmische Spirale, Archimedische Spirale, Fermatsche Spirale
Fermatsche Spirale (grün)	Lituus-Spirale (blau)
Parabel	Kardioide (grün), Zissoide des Diokles (blau)

Weitere Abbildungen
Kurve	Inverse Kurve
Hyperbel	Lemniskate (rot), Trisektrix von Maclaurin (grün)
	Lemniskate
	Trisektrix von Maclaurin (rot)
Sinusoidale Spirale in Polarkoordinaten $r(\varphi )=a\cos(\varphi )^{1/n}$	Kreis (schwarz), Parabel (grün), Hyperbel (blau), allgemein: Sinusoidale Spirale

Stereografische Projektion und Kreisspiegelung

→ Hauptartikel: Stereografische Projektion

Die stereographische Projektion bezieht sich auf einfache Weise auf die Kreisspiegelung, siehe Bild. Seien P und Q zwei Punkte auf der Kugel mit Projektionen P’ und Q’ auf der Ebene. Dann sind P’ und Q’ im Äquatorkreis genau dann Bilder voneinander, wenn P und Q Spiegelungen voneinander in der Äquatorialebene sind.

Mit anderen Worten, wenn:

• P ein Punkt auf der Kugel ist, aber nicht der „Nordpol“ N und nicht der „Südpol“ S,
• P’ das Bild von P in einer stereografischen Projektion ist mit dem Projektionspunkt N und
• Pˮ das Bild von P in einer stereografischen Projektion ist mit dem Projektionspunkt S,

dann sind P’ und Pˮ inversive Bilder voneinander im Einheitskreis. Denn die Dreiecke $\Delta _{NOP'}$ und $\Delta _{Q'OS}$ sind einander ähnliche Dreiecke, weil sie drei gleiche Innenwinkel besitzen, mit der Konsequenz:

${\frac {NO}{OP'}}={\frac {P''O}{OS}}\quad \rightarrow \quad {\frac {R}{OP'}}={\frac {P''O}{R}}\quad \rightarrow \quad P''O={\frac {R^{2}}{OP'}}$

Hilfsmittel für die Inversion am Kreis

Der Inversor von Peaucellier, der Inversor von Hart und der Quadruplanar-Inversor sind mechanische Geräte, die speziell für die Inversion am Kreis konstruiert wurden.

Weblinks

• Vladimir S. Matveev: Inversion am Kreis (Kreisspiegelung). Teil eines Skripts zur Linearen Algebra der Uni Jena (PDF; 828 kB).
• Inversion auf cut-the-knot (engl.)

Literatur

• Coxeter, H. S. M., und S. L. Greitzer: Zeitlose Geometrie. Klett, Stuttgart 1983. 
• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 121–127 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry, S. 43–57). 
• August Adler: Theorie der geometrischen Konstruktionen. G. J. Göschensche Verlagshandlung, Leipzig 1906, III. Abschnitt, Konstruktionen, ausgeführt durch bloßes Schlagen von Kreisbogen (Mascheronische Konstruktionen) – (archive.org [abgerufen am 26. Dezember 2023]). 

Einzelnachweise

en:Inversive geometry