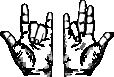Benutzer:Otfried Lieberknecht/30

Entwurf

Als Zahlensystem bezeichnet man die Regeln, nach denen beim Zählen und bei der schriftlichen oder sonstigen Darstellung von Zahlen eine Zahl größer 1, auch Basis genannt, als Einheit höherer Ordnung aufgefaßt und regelmäßig an die Stelle der in ihr enthaltenen Einheiten niederer Ordnung gesetzt wird, um die Erfassung von Zahlen, die größer sind als die Basis, zu vereinfachen und ihre Darstellung durch Einsparung von Zeichenbedarf zu ökonomisieren. Ausentwickelte Zahlensysteme sezten außer der Basiszahl regelmäßig auch deren Vervielfachungen mit sich selbst (ihre Potenzen) als Einheiten aufsteigender Ordnung an (exponentielles Zahlensystem). Minder entwickelte Systeme verwenden nur die Basiszahl oder gegebenenfalls auch Vervielfachungen der Basis mit anderen Faktoren, aber nicht speziell ihre Potenzierungen, als Einheiten höherer Ordnung.

Die meisten Zahlwortsysteme der natürlichen Sprachen verwenden ein Zahlensystem mit der Basis 10 (Dezimalsystem), das auch den meisten historischen Zahlschriften zugrundeliegt. Weltweit am zweithäufigsten ist ein System auf der Basis 20 (Vigesimalsystem) oder ein Mischsystem, in dem bis 100 auf der Basis 20 und weiter dannn auf der Basis 10 gezählt wird. Die besondere Verbreitung dieser beiden Basiszahlen und ihre häufige Verbindung mit einer Hilfsbasis 5 ist nach Befunden der Anthropologie und der Sprachwissenschaft auf Techniken des Zählens mit den Fingern und den Zehen zurückzuführen. In digitalen Rechenanlagen, die Informationen binär mithilfe entgegengesetzter Spannungszustände des Typs 'ein'/'aus' codieren, überwiegen demgegenüber Zahlensysteme, die die Zahl 2 oder eine ihrer Potenzen (2, 4, 8, 16) als Basis zugrundelegen.

Für die Systematisierung der Darstellung natürlicher Zahlen eignet sich jede ganzzahlige Basis größer 1 (polyadisches Zahlensystem). Durch Einbeziehung negativer Potenzen der Basis, die jeweils eine Bruchzahl ergeben, kann ein solches System auch für die Darstellung rationaler Zahlen und näherungsweise Darstellung reeller Zahlen erweitert werden. Zahlensysteme mit negativer Basis, deren Potenzen alternierend negative und positive Zahlen ergeben, spielen für den sprachlichen Ausdruck von Zahlen und die historischen Zahlschriften keine Rolle, ihr Prinzip eignet sich aber für technische Anwendungen wie die negativ binäre Zahlencodierung in der Digitaltechnik.

Benennung und definitorische Merkmale

Basis und Basisverwendung

Ein Zahlensystem ist definiert durch die Größe und Art seiner Basis, die jeweils eine positive oder in speziellen technischen Anwendung auch eine negative ganze Zahl ist, und durch die Verwendungsweise der Basis. Bei letzterer ist zu unterscheiden zwischen potenzierender Basisverwendung, bei der nicht nur die Basis sondern auch die Vervielfachungen der Basis mit sich selbst Einheiten aufsteigender (bei negativen Potenzen absteigender) Ordnung bilden (exponentielles Zahlensystem), und nicht-potenzierender Basisverwendung, bei der eine Zahl als Zusammenfassung der in ihr enthaltenen Einheiten wiederholt oder vervielfacht und mit Einheiten niederer Ordnung additiv verknüpft wird (x × B + y), ohne daß auch ihre Potenzen Einheiten höherer Ordnung bilden.

Nichtpotenzierende Basisverwendung kennzeichnet rudimentär entwickelte Zahlensysteme mancher natürlicher Sprachen und Kerbschriften, kann aber auch als Verwendung einer oder mehrerer Hilfsbasen in systematisch geregelter Verbindung mit potenzierender Verwendung einer anderen Basiszahl auftreten, wie z.B. in der römischen Zahlschrift, die Potenzen der Basis 10 mit einer Hilfsbasis 5 vervielfacht, oder als Systemabweichung, bei der vorüberhend auf eine andere als die sonst verwendete Basiszahl zurückgegriffen wird, z.B. frz. soixante-dix („sechzig [und] zehn“), quatre-vingt („vier [mal] zwanzig“) und quatre-vingt-dix („vier [mal] zwanzig [und] zehn“) für 60, 70 und 80 als Relikt eines älteren Vigesimalsystems im Rahmen eines ansonsten dezimal basierten Zahlwortsystems.

Benennung von Zahlensystemen

Die sprachliche Benennung eines Zahlensystems richtet sich nach der Größe seiner Basis und wird herkömmlich im Rückgriff auf Ableitungen aus griechischen oder lateinischen Zahlwörtern vorgenommen. Die lateinischen Namen werden dabei für Basen unter 10 aus den Kardinal- oder alternativ aus den Distributivzahlwörtern, für Basen ab 10 hingegen aus den Ordinalzahlwörtern, speziell im Fall der Basen 16 und 60 auch in Form griechisch-lateinischer Hybridbildungen („hexadezimal“ statt sedezimal oder senidenär, „hexagesimal“ statt sexagesimal oder sexagenär).

Basis	lateinisch			Name	griechisch
	kardinal	ordinal	distributiv
1	unus	primus	singulari(u)s	Unär-, Singulärsystem	monadisch
2	duo	secundus	binarius	Dual-, Binärsystem	dyadisch
3	tres	tertius	ter-, trinarius	Ternär-, Trinärsystem	triadisch
4	quattuor	quartus	quaternarius	Quaternärsystem	tetradisch
5	quinque	quintus	quinarius	Quinärsystem	pentadisch
6	sex	sextus	senarius	Senär-, Senarsystem	hexal, hexadisch
7	septem	septimus	septenarius	Septenär-, Septenarssystem	heptadisch
8	octo	octavus	octonarius	Oktalsystem	oktal, oktadisch
9	novem	nonus	novenarius	Nonärsystem	enneadisch
10	decem	decimus	denarius	Dezimal-, Denärsystem	dekadisch
12	duodecim	duodecimus	duodenarius	Duodezimal-, Duodenärsystem	dodekadisch
16	sedecim	sextus decimus, sedecimus	sedenarius	Sedezimal-, Hexadezimalsystem	hexadekadisch
20	viginti	vigesimus	vicenarius	Vigesimalsystem	(e)ikosadisch
30	triginta	trigesimus	tricenarius	Trigesimalsystem	triakontadisch
60	sexaginta	sexagesimus	sexagenarius	Sexagesimal-, Hexagesimalsystem	hexakontadisch

Bei kombinierter Verwendung einer Basis mit einer Hilfsbasis oder anderen Formen der Basismischung werden entsprechend zusammengesetzte Benennungen gebildet (z.B. dezimal-quinär, sexagesimal-dezimal). Ohne den Zusatz „negativ“ beziehen sich die lateinisch oder griechisch entlehnten Namen von Zahlensystemen immer auf Verwendung der betreffenden positiven Zahl als Basis.

Zahlensysteme mit einer Basis > 1 werden zur Unterscheidung vom monadischen oder Unärsystem (Basis 1) zusammenfassend als polyadische Zahlensysteme bezeichnet. Zahlensysteme mit potenzierender Basisverwendung bezeichnet man als exponentielle Zahlensysteme.

Abgrenzung von Zahlen- und Zahlzeichensystem

Ein Zahlensystem (engl. number system) ist Teil der umfassenderen Regeln eines Zahlzeichensystems (numeral system), also eines Zeichensystems für die Darstellung von Zahlen, das seinerseits sprachlich (durch Zahlwörter), schriftlich (durch Zahlschrift) oder in einem anderen Medium (z.B. durch Gebärden, Rechensteine, Lichtsignale, elektronische Spannungszustände) realisiert werden kann. Der verbreitete sprachliche Usus, Zahlzeichen und deren Schrift- oder sonstige Zeichensysteme als „Zahlen“ zu bezeichnen (z.B. „römische Zahlen“, „arabische Zahlen“, „Fingerzahlen“) hat es allerdings mit sich gebracht, daß auch der Ausdruck „Zahlensystem“ nicht immer auf das Zahlensystem im engeren und eigentlichen Sinn beschränkt wird, soweit es durch seine Basis und deren arithmetische Verwendungsweise definiert ist, sondern dieser Ausdruck in seiner Bedeutung pars pro toto auch auf das Zahlzeichensystem ausgedehnt oder übertragen wird, dem ein Zahlensystem zugrundeliegt. Wenn etwa vom „römischen Zahlensystem“ die Rede ist, muß der Leser oder Hörer deshalb aus dem Zusammenhang erraten, ob bloß im übertragenen Sinn die römische Zahlschrift oder aber tatsächlich speziell das ihr zugrundeliegende Zahlensystem gemeint ist, das Zahlen anhand einer Basis 10 und Hilfsbasis 5 zerlegt.

Diese verkürzende Gleichsetzung von Zahlen- und Zahlzeichensystem kann unter Umständen unproblematisch sein, wenn das Gemeinte unzweideutig aus dem Kontext hervorgeht, sie birgt aber ein besonderes Potential für mißverständliche oder sachlich falsche Aussagen, wenn es speziell darum geht, Zahlen- und/oder Zahlzeichensysteme in ihren Strukturmerkmalen zu bestimmen und zu typologisieren und hierbei auch die Abhängigkeiten zwischen Zeichensytem und arithmetischer Basis zu beschreiben. Denn ein Zahlzeichensystem ist in seinem Zeicheninventar und den Regeln zur Verwendung dieser Zeichen zwar eng an das zugrundeliegende Zahlensystem gebunden, so daß jede Änderung der Basis oder ihrer Verwendungsweise auch mehr oder weniger weitreichende Änderungen des Zeichensystems nach sich ziehen würde. Umgekehrt besteht eine solche Abhängigkeit jedoch nicht, sondern jedes Zahlensystem kann mit gleicher Basis und gleicher arithmetischer Verwendungsweise dieser Basis prinzipiell in mehreren verschiedenen und auch verschieden gearteten Zeichensystemen realisiert werden. So liegt das „römische Zahlensystem“ mit der Basis 10 und Hilfsbasis 5 nicht nur der römischen Zahlschrift, sondern auch dem römischen Abacus und zahlreichen nichtrömischen und vorrömischen Zahlzeichensystemen zugrunde.

Zeichensysteme für die Darstellung von Zahlen und hierbei besonders solche mit einer Basis > 1 werden nach der Art der Zuordnung ihrer Zeichen zu den höheren Einheiten des zugrundeliegenden Zahlensystems (zu den Potenzwerten der Basis, wenn es sich um ein exponentielles Zahlensystem handelt) unterschieden als additive (mit eigenen Zeichen für diese höheren Einheiten) oder positionelle (mit Zeichen nur für die Zählung der Häufigkeit des Auftretens dieser Einheiten in einer gegebenen Zahl), jeweils auch noch mit mehreren Untertypen, die sich ihrerseits nach der Art ihrer kumulativen, multiplikativen oder beziffernden Bildungsweise der Teilausdrücke zu den in einer Zahl jeweils enthaltenen höheren Einheiten unterscheiden (siehe Strukturtypen der Zahlendarstellung). Da jedes Zahlensystem mit einer ganzzahligen Basis > 1 sowohl in positioneller wie auch in additiver Darstellungsweise realisiert werden kann, jedes Zahlensystem mit einer ganzzahligen Basis > 3 auch in jedem historisch bekannten Untertyp positioneller und additver Darstellung, beschreiben die Attribute „additiv“ und „positionell“ keine Strukturmerkmale dieser Zahlensysteme, sondern Strukturmerkmale der darstellenden Zahlzeichensysteme. Wenn in der Literatur trotzdem manchmal von „positionellen“ bzw. „additiven Zahlensystemen“ die Rede ist, sind deshalb der Sache nach nicht wörtlich Typen von Zahlensystemen, sondern Typen von Zahlzeichensystemen gemeint.

Lehrbücher der angewandten Mathematik und Informatik, die Zahlensysteme unter der Bedingung einer möglichst ökonomischen und und maschinell prozessierbaren Darstellungsweise betrachten, gehen hierbei in der Regel von beziffernd-positioneller Darstellung polyadischer Zahlensysteme (Basis > 1) als dem allgemein leistungsfähigsten Typ aus und behandeln ansonten manchmal noch additive Darstellung auf der Grundlage eines Unärsystems (Basis = 1). Aufgrund dieser thematischen Beschränkung ist es dann meist üblich, bei der Beschreibung eines Zahlensystems auch die Mindestanzahl der für seine Darstellung erforderlichen Zeichen als definitorisches Merkmal anzugeben, weil sie beim Unärsystem in additiver Darstellung und bei polyadischen Zahlensystemen in beziffernd-positioneller Darstellung, bei den letzteren jeweils unter Einschluß eines Leerzeichens mit dem Wert 0, jeweils genau der Größe der Basis entspricht. Bei anderen positionellen (nämlich kumulativ-positionellen) Zahlzeichensystemen mit einer Basis > 1 beträgt die Mindestanzahl benötigter Zeichen (einschließlich eines Äquivalents des Zeichens für 0) jedoch unabhängig von der Größe der Basis stets 2, bei additiven Zahlzeichensystemen ist dieser Wert (ohne ein Zeichen für 0) ebenfalls nicht abhängig von der Basis, sondern vom Exponenten der größten darzustellenden Basispotenz und außerdem von der jeweiligen (kumulativen, multiplikativen oder beziffernden) Bildungsweise der Teilausdrücke für die einzelnen Potenzbereiche. Die Mindestanzahl der benötigten Zahlzeichen gehört deshalb nicht zu den Strukturmerkmalen eines Zahlensystems, sondern ist abhängig vom Strukturtyp des darstellenden Zahlzeichensystems.

Exponentielle Zahlensysteme

Grundstruktur

Ein exponentielles Zahlensystem ist definiert durch eine beliebige, positive oder negative ganze Zahl B ≠ 0, deren Potenzen B⁰, B¹, B² ... Bⁿ die Zähleinheiten aufsteigender Ordnung des Systems bilden, bei Einbeziehung von Bruchzahlen ebenso auch die negativen Potenzen absteigender Ordnung B^-1, B^-2 ... B^-n. Die Potenz B⁰ hat dabei unabhänig von der Größe der Basis immer den Wert 1 und bildet die Grundeinheit des Systems.

Jeder Exponent begründet einen nach ihm benannten Zählbereich eigener Ordnung (Ordnung 0, Ordnung 1, Ordnung 2, usf., negativ Ordnung -1, -2, usf.), der in der speziell für die Beschreibung von positionellen Darstellungssystemen geschaffenen Begrifflichkeit auch 'Stelle' und für negative Potenzen 'Nachkommastelle' heißt und dann nicht mit dem Exponenten ab 0, sondern ab 1 gezählt wird (1. Stelle: Ordnung 0, 2. Stelle: Ordnung 1, usf., bzw. 1. Nachkommastelle: Ordnung -1, 2. Nachkommastelle: Ordnung -2, usf.). Die spezifischen Zähleinheiten jeder Ordnung werden allgemeinsprachlich nach dem Potenzwert (Stellenwert) benannt, z.B. in einem Dezimalsystem (Basis 10) als Einer (10⁰), Zehner (10¹, Hunderter (10², Tausender (10³ usf., bei Einbeziehung negativer Potenzen als Zehntel (10^-1, Hundertstel (10^-2, Tausendstel (10^-3 usf. Jede Ordnung besteht aus dem Einfachen des Potenzwertes und denjenigen Hinzufügungen dieses Wertes zu sich selbst, die noch nicht die nächsthöhere Basispotenz ergeben, also aus insgesamt B-1 Ein- und im Faktor jeweils um 1 erhöhten Vielfachen dieses Potenzwertes. So sind z.B. mit einem Ternärsystem (Basis 3) maximal zwei (= 3-1) Einer (Ordnung 0: 1, 2), Dreier (Ordnung 1: 3, 6), Neuner (Ordnung 2: 9, 18), Siebenundzwanziger (Ordnung 3: 27, 54) usf. zu zählen, mit negativen Potenzen maximal zwei Drittel, Neuntel, Siebenundzwanzigstel, oder in einem Dezimalsystem (Basis 10) maximal neun (= 10-1) Einer (Ordnung 0: 1, 2, 3 ... 9), Zehner (Ordnung 1: 10, 20, 30 ... 90), Hunderter bzw. Zehntel, Hundertstel, Tausendstel usf., während speziell bei einem Dualsystem (Basis 2) jede Ordnung nur eine einzige (= 2-1) Einheit enthalten kann, einen Einer (Ordnung 0), Zweier (Ordnung 1), Vierer (Ordnung 2); Achter (Ordnung 3) usf., bzw. ein Halbes, Viertel, Achtel usf., also jeweils nur das Einfache der betreffenden Basispotenz, da bereits deren Verzweifachung die nächsthöhere Potenz ergibt und damit der nächsthöheren Ordnung angehört.

Ein Unärsystem mit Basis 1 kann mit den Potenzen dieser Basis noch keine Einheiten größer als eins und ebenso keine Bruchzahlen kleiner als eins ausbilden, da der Potenzwert unabhängig von der Größe der anwachsenden Exponenten stets 1 bzw. mit negativen Exponenten stets 1/1 'ein Eintel' beträgt, es stellt jedoch als Sonderfall einen für das Verständnis von Zahlensystemen und ihrer Entstehung wichtigern Kontrasttyp zu den polyadischen Zahlensystemen mit potenzierender oder auch nicht-potenzierender Basisverwendung dar. Das Gegenextrem wäre ein Zahlensystem mit einer Basis, die unendlich oder zumindest so groß ist, daß sie bei der zählenden oder schriftlichen Anwendung des Systems niemals erreicht wird.

Zerlegung einer Zahl in enthaltene Basispotenzen

Mithilfe eines Zahlensystems läßt sich eine gegebene natürliche Zahl arithmetisch als Ein- oder Vielfaches der darin enthaltenen Basispotenzen zerlegen. Das für die Darstellung einer Zahl ökonomischste Prinzip, das auch die meisten Zahlzeichensysteme zugrundelegen, ist hierbei die Zerlegung einer Zahl in ihre größtmöglichen Einheiten, also speziell in der Weise, daß man mit der höchsten in der Zahl enthaltenen Basispotenz beginnt und dann, falls ein Rest bleibt, jeweils zur nächstniedrigeren Ordnung fortschreitet, als Beispiel die Zahl 604:

• Dezimalsystem (Basis 10):
  6 × 10² + 0 × 10¹ + 4 × 10⁰
  = 6 × 100 + 0 × 10 + 4 × 1
• Ternärsystem Basis 3):
  2 × 3⁵ + 1 × 3⁴ + 1 × 3³ + 1 × 3² + 0 × 3¹ + 1 × 3⁰
  = 2 × 243 + 1 × 81 + 1 × 27 + 1 × 9 + 0 × 3 + 1 × 1
• Dualsystem (Basis 2):
  1 × 2⁹ + 0 × 2⁸ + 0 × 2⁷ + 1 × 2⁶ + 0 × 2⁵ + 1 × 2⁴ × 2³ + 1 × 2² + 0 × 2¹ + 0 × 2⁰
  1 × 512 + 0 × 256 + 0 × 128 + 1 × 64 + 0 × 32 + 1 × 16 + 1 × 8 + 1 × 4 + 0 × 2 + 0 × 1

In allgemeiner Formulierung gilt für B > 1 und jede natürliche Zahl N:

$N=a_{n}\cdot B^{n}+a_{n-1}\cdot B^{n-1}+\dotsb +a_{2}\cdot B^{2}+a_{1}\cdot B^{1}++a_{0}\cdot B^{0}$

Hierbei ist der Koeffizient a jeweils ein Element aus der Menge der möglichen Faktoren für die B-1 möglichen Ein- und Vielfachen des Potenzwertes, zuzüglich des Wertes 0 für denjenigen Fall, daß für eine Potenz, die niedriger ist als die höchste in der Zahl enthaltene, kein eigener Häufigkeitswert anzugeben ist.

Bei einem System mit unendlich großer oder jedenfalls über 604 liegender Basis wäre 604 dementsprechend in ebensoviele Einheiten B⁰ zu zerlegen (604 × B⁰ = 604 × 1). Das Unärsystem, das mit den Potenzen seiner Basis 1 keine Zähleinheiten > 1 ausbildet und in jedem Potenzbereich höchstens B-1 = 0 Zähleinheiten enthält, kann eine Zahl deshalb nur in die Grundeinheiten 1 zerlegen oder aus ihnen wieder aufbauen (= 1 + 1 + 1 + … + 1 = 604), wie es dem Prinzip nicht-exponentieller Zahlensysteme (oder nicht-potenzierend verwendeter Hilfsbasen) entspricht.

Darstellung einer Zahl als Summe enthaltener Basispotenzen

Die meisten entwickelten Zahlwortsysteme, Zahlschriften und sonstigen auf potenzierender Basisverwendung beruhenden Darstellungssysteme legen diese Zerlegung einer Zahl in ihre Basispotenzen bei der Bildung eines Zahlenausdrucks zugrunde, indem sie für eine gegebene Zahl jeweils angeben, welche in der Zahl enthaltenen Potenzen der Basis, beginnend bei der höchsten, jeweils wie oft in ihr enthalten sind.

Beispiele für die Zahl 604:

• Zahlschriften

• Ägyptische hieroglyphische Zahlschrift (kumulativ-additiv, Basis 10):
  
  = (100 + 100 + 100 + 100 + 100 + 100) + (1 + 1 + 1 + 1)
• Römische Zahlschrift (kumulativ-additiv, Basis 10, mit Hilfsbasis 5 zur Bündelung von je 5 10er-Potenzen, ohne subtraktive Schreibung)
  DCIIII
  = (500 + 100) + (1 + 1 + 1 + 1)
• Chinesische Zahlschrift (multiplikativ-additiv, Basis 10):
  六百四
  = („sechs“ „hundert“) + „vier“
• Griechisch-milesische Zahlschrift (beziffernd-additiv, Basis 10):
  χδ
  = 600 + 4
• Babylonisch-kuneiforme Zahlschrift (kumulativ-positionell, positionelle Basis 60, mit Hilfsbasis 10 zur Bündelung von je 10 60er-Potenzen):
  
  = (10 [× 60]) + (4 [× 1])
• Indisch-arabische Zahlschrift (beziffernd-positionell, Basis 10):
  604
  = (6 [× 100]) + (0 [× 10]) + (4 [× 1])

• Nichtschriftliche Zahlzeichensysteme

• Währungseinheiten Deutsche Mark (kumulativ-additiv, Basis 10, Hilfsbasen 2 und 5)
  
  = (500 + 100) + (2 + 2)
• Deutsche Zahlwörter (multiplikativ-additiv, Basis 10):
  „sechshundertundvier“
  = (6 × 100) + 4
• Fingerzahlen nach Beda Venerabilis (beziffernd-additiv, Basis 10)
  
  

Kleiner, Ring- und Mittelfinger links (Einer): 4, rechts (Tausender): Ruhestellung

Zeigefinger- und Daumenstellung links (Zehner): Ruhestellung, rechts (Hunderter): 6

= { (0 × 1000) + 600 } + { (0 × 10) + 4 }

• Fingerzahlen nach Leonardo da Pisa (beziffernd-additiv, Basis 10)
  
  

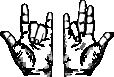
Kleiner, Ring- und Mittelfinger links (Einer): 4, rechts (Hunderter): 6

Zeigefinger- und Daumenstellung links (Zehner) und rechts (Tausender): Ruhestellung

= { (0 × 1000) + 600 } + { 4 + (0 × 10) }

• Klosterabacus (beziffernd-positionell, Basis 10, vereinfacht wiedergegeben mit 9 von 27 Spalten)
  
  = (0 [× 100.000.000]) + ... + (6 [× 100]) + (0 [× 10]) + (4 [× 1])
• Römischer Handabacus (kumulativ-positionell, Basis 10, mit Hilfsbasis 5 zur Bündelung von je 5 10er-Potenzen)
  
  = (0 [× 10.000.000]) + ... + (1 [× 500]) + (1 [× 100]) + (0 [× 10]) + 4 [× 1])

Beziehungen zwischen Zahlen- und Zahlzeichensystemen

Strukturtypen der Zahlendarstellung

Zahlschriften werden herkömmlich als additive und positionelle unterschieden, mit diversen Untertypen und Mischformen, bei deren Unterscheidung und Benennung in der älteren Forschung noch wenig Einheitlichkeit bestand. In jüngerer Zeit hat der kanadische Anthropologe Stephen Chrisomalis diesen typologischen Ansatz methodisch verbessert, durch eine getrennte Betrachtung einerseits der Bildungsweise der „intra-exponentiellen“ Teilausdrücke, die sich jeweils auf einen Potenzbereich beziehen, und andererseits der übergreifenden, „inter-exponentiellen“ Organisation des Gesamtausdrucks, aus der sich erst der Wert der dargestellten Zahl ergibt. Durch diese Unterscheidung wurde es möglich, fünf Strukturtypen exponentiell basierter Zahlendarstellung – drei additive und zwei positionelle – zu definieren, denen sich die meisten exponentiell basierten Zahlschriften eindeutig oder zumindest nach ihrer dominierenden Darstellungsweise zuordnen lassen, und die sich, mit gewissen Einschränkungen besonders bei den Zahlwörtern der natürlichen Sprachen, auch zur Strukturbestimmung nichtschriftlicher Zahlzeichensysteme eignen, sofern diese ebenfalls ein exponentielles Zahlensystem zugrundelegen.

Erforderlich wurde im Rahmen dieses methodischen Neuansatzes auch eine terminologische Neuerung: der Terminus „additiv“ wird von Chrisomalis und der an ihn anknüpfenden jüngeren Forschung nur noch im Sinne von „nicht-positionell“ für einen der beiden entgegengesetzten Typen der (inter-exponentiellen) Bildungsweise von Gesamtausdrücken beibehalten, aber nicht mehr als Terminus für das Prinzip der reihenden Wiederholung gleichwertiger Potenzwertzeichen, das ein im Rahmen positioneller und nicht-positioneller Gesamtdarstellung gleichermaßen mögliches Verfahren zur (intra-exponentiellen) Bildung von Teilausdrücken für die einzelnen Potenzbereiche ist, und als solches nur noch als „kumulativ“, aber nicht mehr, wie in der älteren Forschung, ebenfalls als additiv bezeichnet wird.

Additive Zahlzeichensysteme

Additive Zahlzeichensysteme sind dadurch charakterisiert, daß sie jeder Basispotenz ein eigenes Zeichen ihres einfachen Wertes zuweisen, und unterscheiden sich dann durch das Verfahren, nach dem sie bei der Bildung eines intra-exponentiellen Teilausdrucks diesen Wert vervielfachen, um anzugeben, wie oft die betreffende Basispotenz in der darzustellenden Zahl enthalten ist:

• kumulativ-additiv: das Potenzwertzeichen wird ein oder mehrmals wiederholt, um ein Zwei- oder Mehrfaches seines Wertes darzustellen
• beziffernd: nicht nur das Einfache, sondern auch jedes Vielfache des Potenzwertes wird jeweils durch ein eigenes Zeichen ausgedrückt
• multiplikativ: das Potenzwertzeichen wird mit einem anderen Zeichen (oder aus mehreren Zeichen gebildeten Teilausdruck) verknüpft, um das Produkt aus beiden Werten auszudrücken

Additive Zahlzeichensysteme pflegen ihre Teilausdrücke zwar ebenso wie positionelle nach der auf- oder absteigenden Größe der Basisexponenten anzuordnen, diese Anordnungsweise dient jedoch nur dazu, die Lesung und Schreibung zu erleichtern und hat keinen Einfluß auf den Wert des Gesamtausdrucks, der auch bei veränderter Anordnung der Teilausdrücke stets gleich bleibt.

Kumulativ-additiv

In einem kumulativ-additiven Zahlzeichensystem wird für jede Basispotenz ein eigenes Zeichen verwendet und dieses entsprechend der Häufigkeit ihres Wertes in kumulativer Zeichenwiederholung ein oder mehrfach, bis zu B-1 mal, gesetzt. Der Wert eines aus solchen Teilausdrücken gebildeten Gesamtausdrucks ergibt sich, indem man bei jedem Teilausdruck den Wert des verwendeten Zeichens (den jeweiligen Potenzwert) mit der Anzahl seiner Verwendungen (dem jeweiligen Häufigkeitswert) multipliziert und aus diesen Produkten dann die Summe bildet. Da für jeden Potenzwert, beginnend bei B⁰ = 1, ein eigenes Zeichen benötigt wird, hängt das Inventar der benötigten Zeichen ab von der Größe der darzustellenden Zahlen, sein Mindestumfang U beträgt E + 1, mit E als dem Exponenten der größten darzustellenden Basispotenz.

Ägyptische hieroglyphische Zahlschrift
100	101	102	103	104	105	106
1	10	100	1000	10.000	100.000	1.000.000
Beispiel 4.031.525:

Ein bekanntes additiv-kumulatives System ist die ägyptische hieroglyphische Zahlschrift, der ein exponentielles Zahlensystem auf der Basis 10 zugrundeliegt. Ihr Zeicheninventar umfaßt sieben Eigenzeichen für die Potenzwerte 1 bis 1.000.000 (= 10⁶), von denen jedes ein- bis neunfach gesetzt wird, um die bis zum Erreichen der nächsthöheren Potenz möglichen B-1 Ein- und Vielfachen seines Wertes auszudrücken. Als höchster Wert kann kann durch neunfache Schreibung jedes dieser sieben Potenzwertzeichen, also mit einem Zahlenausdruck von insgesamt 63 Zeichen Länge, die Zahl 9.999.999 geschrieben werden.

Viele Zahlschriften und Zahlzeichensysteme, die sich der kumulativen Zeichenwiederholung bedienen, setzen bei der Bildung der Teilausdrücke zur Einsparung solcher Zeichenwiederholungen auch noch eine Hilfsbasis ein, einen ganzzahligen Teiler H der Basis B, indem sie das H-fache eines Potenzwertes durch ein für jeden Potenzbereich spezifisches Eigenzeichen ausdrücken. Bekanntester Vertreter dieses Typs ist die römische Zahlschrift, die Potenzwertzeichen der Basis 10 (I, X, C, usf.) kumulativ wiederholt, aber anhand einer Hilfsbasis 5 das Fünffache eines Potenzwertes jeweils durch ein eigenes Zeichen bündelt (V, L, D, usf.), so daß jedes Potenzwertzeichen nur höchstens vier (statt neun) mal hintereinandergeschrieben zu werden braucht.

Römische Zahlschrift
100	100 × 5	101	101 × 5	102	102 × 5	103	103 × 5	104	104 × 5	105
1	5	10	50	100	500	1000	5000	10.000	50.000	100.000
Beispiel 20.742:

Da die Hilfsbasis in diesem Fall in ihrem Wert die Hälfte der Basis beträgt, können ihre Zeichen nicht auch ihrerseits in kumulativer Zeichenwiederholung erscheinen, da bereits die Verdopelung ihres Wertes jeweils den Wert der nächsthöheren Potenz ergibt, während bei Verwendung eines niedrigeren Teilers der Basis als Hilfsbasis auch deren Zeichen kumulativ wiederholt werden können. Nach ihrem Teilungsverhältnis zur Basis werden die für Verwendung einer Hilfsbasis benötigten Zeichen auch Halbzeichen (H = B/2), Drittelzeichen (H = B/3), Vierteilzeichen (H = B/4) usf. genannt. Kumulativ-additive Zahlschrift kann auch mehrere solche Hilfsbasen verwenden. Da bei Verwendung einer Hilfsbasis für jeden Potenzbereich ein eigenes Zeichen benötigt wird, das den Wert der Basispotenz mit dem Wert der Hilfsbasis vervielfacht, vergrößert sich theoretisch auch das Mindestinventar der benötigten Eigenzeichen mit jeder Hilfsbasis um die gleiche Anzahl U der schon für die Potenzwerte benötigten Zeichen. In der Praxis vergrößert sie sich oft nur um den Wert U-1, wenn dort darauf verzichtet wird, dem höchsten Potenzwertzeichen noch ein vervielfachendes Zeichen überzuordnen.

Proto-kuneiforme Zahlzeichen der Sumerer

Bei Aussagen über den Umfang des Zeicheninventars ist im übrigen zu beachten, daß diese Zeichen auch ihrerseits regelhaft aus untergeordneten Zeichenelementen oder -segmenten zusammengesetzt sein können. So wurden die archaischen, proto-kuneiformen Zahlzeichen der Sumerer im 4. Jahrtausend vor Chr. durch kreis- und kegelförmige Abdrücke eines Griffels in Lehm oder Ton erzeugt, zum Beispiel in der Weise, daß auf der Grundlage eines Zahlensystems mit Basis 60 und Hilfsbasis 10 die Potenzwertzeichen für 1, 60 und 3600 sowie für deren Verzehnfachungen durchgängig durch Vergrößerung und Kombination der beiden Grundelemente Kreis und Kegel gebildet wurden. Noch einfacher bildete die etruskische Zahlschrift ihre Potenzwertzeichen (1), (10) und (100) auf der Basis 10 als Strich, Kreuz und Durchstreichung des Kreuzes (sechsstrahliger Stern) aus einem einzigen Strich-Element, Zeichen für höhere Potenzwerte auch durch Verbindung von Strich oder Punkt mit einem Kreiselement, während die Verfünffachungen (5) und (50) anhand der Hilfsbasis 5 jeweils durch Halbierung des nächsthöheren Potenzwertzeichens entstanden, was dann auch zum Vorbild für die archaischen Zeichen der römischen Zahlschrift wurde. Für die Bestimmung des aadditiven Strukturtyps und seines Zeichenbedarfs ist jedoch nicht die Bildungsweise oder der einzelnen Zeichen maßgeblich, die ihrerseits arithmetisch (als Verdoppelung oder Halbierung, Vervielfachung oder Teilung) motiviert sein kann, sondern entscheidend ist die Zuordnungsweise der Zeichen zur Basis und deren Potenzen, wie sie bei der Bildung der Teilausdrücke zu den einzelnen Potenzbereichen innerhalb eines numerischen Gesamtausdrucks zum Tragen kommt.

Im Bereich der Zahlwörter spielt das kumulative Prinzip nur eine marginale, und dann meist auf einfache Wiederholung eines Zahlwortes zur Verdoppelung seines Wertes beschränkte Rolle, ausgebildete kumulativ-additive Systeme gibt es dort nicht. Ansonsten sind dem zahlschriftlichen Prinzip am ehesten Wertzeichensysteme zu vergleichen, in denen Steine, Muscheln, Spielmarken, Münzen oder sonstige Wertzeichen nach Form, Farbe, Gewicht oder anderen Merkmalen unterschieden und den Potenzwerten einer Basis als exponentiell aufsteigende Werteinheiten zugeordnet sind: das Auslegen eines Wertbetrages in den größtmöglichen Einheiten des Wertzeichensystems entspricht dann der Darstellungsweise kumulativ-additiver Zahlschrift.

Beziffernd-additiv

Ein beziffernd-additives Zahlzeichensystem verwendet nicht nur für jeden einfachen Potenzwert seiner Basis, sondern auch für jedes bis zum Erreichen der nächsthöheren Potenz mögliche Vielfache dieses Wertes ein Eigenzeichen, so daß bei der Darstellung einer Zahl für jeden Potenzbereich nur ein einziges Zeichen verwendet wird, dem das Produkt aus Häufigkeits- und Potenzwert als fester Wert zugeordnet ist.

Griechisch-milesische Zahlschrift
Α α	Β β	Γ γ	Δ δ	Ε ε	Ϝ ϝ, Ϛ ϛ	Ζ ζ	Η η	Θ θ
1	2	3	4	5	6	7	8	9
Ι ι	Κ κ	Λ λ	Μ μ	Ν ν	Ξ ξ	Ο ο	Π π	Ϙ ϙ
10	20	30	40	50	60	70	80	90
Ρ ρ	Σ σ	Τ τ	Υ υ	Φ φ	Χ χ	Ψ ψ	Ω ω	, Ϡ ϡ
100	200	300	400	500	600	700	800	900

In der Geschichte der ägyptischen Zahlschrift entstand das beziffernd-additive als Vereinfachung des kumulativ-additiven Prinzips, indem bei der kursiven Schreibung hieroglyphischer Zahlschrift die Wiederholungen der Potenzwertzeichen jeweils zu einem neuen eigenen Zeichen zusammengezogen wurden. Bekanntester Vertreter dieses Strukturtyps ist die griechisch-milesische Zahlschrift, die seit dem 6. Jahrhundert vor Chr. belegt ist und wahrscheinlich nach ägyptisch kursivem (demotischem) Vorbild entstand. Sie beruht ebenfalls auf einem exponentiellen Zahlensystem auf der Basis 10 und verwendet zur Schreibung der Zahlen die Lautbuchstaben des griechischen Alphabets, wobei zwei seither lautschriftlich obsolet gewordene Buchstaben in ihrer alphabetischen Stellung als Zahlzeichen beibehalten wurden (Digamma bzw. Vau, später mit Stigma gleichgesetzt, außerdem Koppa) und ein weiterer Buchstabe (San oder Sampi), der schon zur Entstehungszeit dieser Zahlschrift lautschriftlich nicht mehr benötigt wurde, an den Schluß der Zahlzeichenreihe angehängt wurde, um eine Gesamtzahl von 27 (3 × 9) Zeichen zu erhalten, denen sich die Einer 1 bis 9, die Zehner 10 bis 90 und die Hunderter 100 bis 900 zuordnen ließen.

Das Grundinventar U der mindestens benötigten Zahlzeichen beträgt bei einem beziffernd-additiven System (E + 1) × (B - 1), weil für jeden darzustellenden Potenzbereich B-1 Ein- und Vielfache des Potenzwertes jeweils mit einem eigenen Zeichen auszudrücken sind.

Fingerzahlen nach Beda Venerabilis

Die Zeichenreihen für die einzelnen Potenzbereiche können dabei allerdings auch auseinander abgeleitet sein. Das von Beda Venerabilis beschriebene System der römischen Fingerzahlzeichen stellte auf der Basis 10 mit der linken Hand durch neun Fingerstellungen von kleinem, Ring- und Mittelfinger die Einer und durch neun Fingerstellungen von Zeigefinger und Daumen die Zehner dar. Diese beiden Zeichenreihen wurden um zwei daraus abgeleitete Zeichenreihen erweitert, indem die gleichen 9 + 9 Fingerstellungen auf der rechten Hand jeweils vertikal gespiegelt die Hunderter und die Tausender anzeigten, so daß mit beiden Händen bereits die Zahlen 1 bis 9.999 darstellbar waren. Vier Potenzbereiche wurden folglich nicht mit vier eigenständigen Zeichenreihen, sondern mit zwei Zeichenreihen in jeweils zwei durch vertikale Spiegelung unterschiedenen Erscheinungsvarianten dargestellt.

Zahlschrift der Zisterzienser

Auf die Spitze getrieben erscheint dieses Prinzip in einer mittelalterlichen, vor allem in Handschriften der Zisterzienser verbreiteten Zahlschrift, die für die ersten vier Potenzbereiche der Basis 10 jeweils die gleichen neun Zeichen, aber in vier Varianten horizontaler und vertikaler Spiegelung, verwendet. Da die Zeichen der höheren drei Potenzbereiche aus denen des ersten Potenzbereiches abgeleitet sind, kann man dieses System letztlich auch bereits als ein beziffernd-positionelles einstufen, bei dem die Zeichen lediglich den Häufigkeitswert anzeigen, während der damit zu multiplizierende Potenzwert durch ihre Position innerhalb des Gesamtausdrucks (und in diesem Fall auch durch ihre Stellung zur Spiegelachse) ausgedrückt wird.

Multiplikativ-additiv

Chinesische Zahlschrift			Beispielzahl 4539
	Klassisch	Shang Zeichen	Klassisch	Shang
1	一		四 千 五 百 三 十 九
2	二
3	三
4	四
5	五
6	六
7	七
8	八
9	九
101	十
102	百
103	千
104	萬

In einem multiplikativ-additiven Zahlzeichensystem wird die Vervielfachung eines Potenzwertes weder durch kumulative Wiederholung des Potenzwertzeichens, noch durch ein eigenes Zeichen für das Produkt aus Potenz- und Häufigkeitswert, sondern dadurch dargestellt, daß das Potenzwertzeichen multiplikativ mit einem Eigenzeichen oder aus mehreren Zeichen gebildeten Ausdruck für den Häufigkeitswert verknüpft wird. Die Teilausdrücke für die einzelnen Potenzbereiche sind deshalb jeweils erst durch Multiplikation beider Werte arithmetisch aufzulösen, ehe sie in der Summe die dargestellte Zahl als Wert des Gesamtausdrucks ergeben.

Die Mindestanzahl U der für ein multiplikativ-additives System benötigten Zeichen setzt sich zusammen einerseits aus der Anzahl der für die Häufigkeitswerte benötigten Eigenzeichen für die Einer (B - 1) und andererseits der Anzahl der benötigten Potenzwertzeichen (E + 1), wobei das Zeichen für 1 = B⁰ in beiden enthalten ist, im Ergebnis deshalb U = B + E - 1. Das multiplikative Verfahren eignet sich allerdings in besonderem Maße dazu, auch Häufigkeitsausdrücke größer als B - 1 multiplikativ mit einem Potenzwertzeichen zu verknüpfen und so durch das Produkt aus beidem den Wert der nächsthöheren Potenz zu überschreiten, mit der Folge, daß für die Schreibung größerer Zahlen zur Einsparung des Bedarfs von Potenzwertzeichen davon abgesehen werden kann, bei der Bildung des Zeicheninventars jede nächsthöhere Basispotenz mit einem solchen Eigenzeichen zu versehen. Die angegebene Formel gilt deshalb nur, wenn der Exponent der mit Eigenzeichen benannten Basispotenzen sich regelmäßig um eins erhöht.

Das multipliativ-additive Verfahren dominiert allgemein im Bereich der sprachlichen Zahlwörter mit exponentiellem Zahlensystem und wurde zahlschriftlich besonders in der auf logographischen Zahlwortzeichen beruhenden chinesischen Zahlschrift adaptiert. Dort werden auf der Grundlage eines exponentiellen Zahlensystems mit der Basis 10 die Einer 1 bis 9 mit neun alleinstehenden Eigenzeichen geschrieben, von denen in der zuerst während der Qin-Dynastie (221-226 v. Chr.) belegten, bis heute grebräuchlichen klassischen Form dieser Zahlschrift die ersten drei kumulativ gebildet sind. Für die Schreibung größerer Zahlen werden diese Eigenzeichen dann als Multiplikatoren mit den betreffenden Potenzwertzeichen verknüpft, wobei das Potenzwertzeichen für 10 bei Zahlen unter 20 gewöhnlich ebenfalls alleinstehend, also ohne Multiplikator 1, erscheint. Für die Schreibung großer Zahlen kann das Potenzwertzeichen für 10⁴ auch mit einem multiplikativen Ausdruck > 9 < 1000 verknüpft werden, außerdem gibt es drei verschiedene Systeme, elf Zeichen für Basispotenzen mit einem Exponenten > 4 zu bewerten: ein niedriges System, bei dem der Exponent normal im Abstand 1 von 10⁴ bis 10¹⁴ ansteigt, ein mittleres System, bei dem er im Abstand 2 von 10⁴ auf 10⁸ und dann im Abstand 8 bis 10⁸⁰ ansteigt, und ein hohes System, bei dem er im Abstand 2ⁿ von 10⁴, 10⁸ bis 10⁴⁰⁹⁶ ansteigt.

Die älteste Form oder Vorstufe dieser Zahlschrift findet sich auf Knochenorakeln der Shang-Dynastie seit dem Ausgang des 14. Jahrhunderts v. Chr., wo die multiplikativen (für die Zehner 10 bis 40 kumulativen) Teilausdrücke jeweils zu einem einzelnen Zeichen zusammengezogen werden ( 10, 20, 30, 40, 50, 80; 100, 200, 300, 500, 600; 1000, 3000, 4000, 5000), so daß man auch von einer beziffernd-additiven Vorstufe sprechen könnte.

Bei nicht-sprachlichen und nicht-schriftlichen Zahlzeichensystemen spielt das multiplikativ-additive Prinzip keine besondere Rolle.

Additive Mischformen

Mischungen der additiven Strukturtypen können durch Vereinfachung entstehen, indem kumulative oder multiplikative Teilausdrücke zu beziffernden Eigenzeichen zusammengezogen werden, wie bei der geschichtlichen Transformation der ägyptischen kumulativ-additiven Zahlschrift zu einer beziffernd-additiven als Folge kursiver Schreibungen und Ligaturen. Vor allem aber treten sie in der Weise auf, daß kumulativ- oder beziffernd-additive Zeichensysteme ihr Grundprinzip nur bis zu einer bestimmten Zahlengrenze einhalten und dann zu multiplikativen Schreibweisen übergehen.

Brahmi und Aramäisch

Aramäische Zahlschrift

Brahmi Zahlschrift

Ein Beispiel hierfür ist die seit dem 8. Jahrhundert vor Chr. belegte aramäische Zahlschrift, die ein Zahlensystem mit Basis 10 und Hilfsbasis 20 zugrundelegt und mit Zeichen für 1, 10 und 20, manchmal auch mit einem Eigenzeichen für 5, die Zahlen 1 bis 99 kumulativ-additiv schreibt, während die Zeichen für 100 und 1000 gewöhnlich nicht kumulativ wiederholt, sondern einzeln mit multiplizierenden Teilausdrücken verknüpft wurden. Es handelt sich insofern um ein Hybridsystem additiven Typs, mit kumulativ Schreibung der der Teilausdrücke für Zahlen < 100 und multiplikativer Schreibung der Teilausdrücke für Zahlen ≥ 100, das in ähnlicher, meist von aramäischem Vorbild abhängiger Form auch in zahlreichen weiteren Zahlschriften des östlichen Mittelmeerraumes begegnet. Ein ähnliches Bild, aber mit beziffernd-additivem Prinzip für die Schreibung niederiger Zahlen und Mischung beziffernder und multiplikativer Schreibweisen im höheren Zahlenbereich, zeigt die seit dem 3. Jahrhundert vor Chr. bezeugte indische Brahmi-Zahlschrift. Sie verwendet auf der Grundlage eines Dezimalsystems beziffernd-additive Zeichen (deren erste drei I, II, III kumulativ gebildet werden) für die Schreibung der Zahlen 1 bis 99, während für größere Zahlen teils die Potenzwertzeichen für 100 und 1000 mit niederwertigeren Zeichen multiplikativ verknüpft werden, teils auch (speziell für die Hunderter 200 bis 500 und die Tausender 2000 bis 5000) beziffernde Eigenzeichen verwendet wurden, die aus Ligaturen solcher Verknüpfungen entstanden zu sein scheinen.

Römisch

Römische Zahlschrift der Kaiserzeit
kumulativ-additiv
1	5	10	50	100	500	1000
5000	10.000	50.000	100.000
multipliziert mit 1000
1000	5000	10.000	50.000	100.000	500.000	1.000.000
multipliziert mit 100.000
100.000	500.000	1.000.000	5.000.000	10.000.000	50.000.000	100.000.000

Die römische Zahlschrift besaß elf Potenzwert- und Halbzeichen für die kumulativ-additive Schreibung von Zahlen bis zum Potenzbereich 10⁵, seit dem Ausgang der republikanischen Zeit kamen jedoch Schreibungen von Zahlen ≥ 10³ mit einem auf die ersten sieben Zeichen reduzierten Inventar auf, deren Wert durch Überstreichung vertausendfacht und seit der frühen Kaiserzeit durch Einrahmung auch verhunderttausendfacht wurde. Während im älteren Stil bis 4.999.999 geschrieben werden konnte, war mit Überstreichung und Rahmen die Schreibung bis 499.999.999 möglich, als höchste tatsächlich geschriebene Zahl ist aber außer einem vereinzelten Beleg für 10⁸ nur die folgende bekannt::

• CCCLVIII LXIII CXX
  = 358'63'120 = 35.863.120

Sieht man Überstreichung und Rahmung nur als diakritische Mittel, um aus den ersten sieben Zeichen höherwertige Zeichen für die Fortsetzung der unverändert kumulativ-additiven Schreibung abzuleiten, so hat man es im Ergebnis immer noch mit einem rein additiv-kumulativen System mit nunmehr 17 Zeichen – 6 unmarkierten, 4 überstrichenen und 7 gerahmten – zu tun. Insoweit die diakritischen Markierungen aber eine Multiplikation mit 1000 oder 100.000 und (ihre Abwesenheit eine Multiplikation mit 1) ausdrücken, ergibt sich zugleich die Deutungsmöglichkeit eines übergreifend multiplikativ-additiven Systems, in dem die Zahlen 10³ und 10⁵ als untereinander nicht-exponentiell gesteigerte Einheiten höherer Ordnung fungieren. Weil die zu multiplizierenden Werte nicht durch eigene Zeichen, sondern nur durch diakritische Markierungen der Zeichen und sekundär durch deren Gruppierung ausgedrückt werden, konvergiert diese kaiserzeitliche Variante der römischen Zahlschrift in der Tendenz auch bereits einem kumulativ-positionellen Zeichensystem. Bei gelentlichen Schreibungen des Typs III.XII.DC. = 3'12'600 = 312.600 oder XII.L.D. = 12'50'500 = 1.250.500, bei denen Rahmung und Überstreichung weggelassen und der Potenzwertbezug (auf 10⁵, 10³, 10⁰) der kumulativen Teilausdrücke nur noch durch deren Position innerhalb des Gesamtausdrucks angezeigt war, wurde ein solches kumulativ-positionelles System tatsächlich erreicht.

Die mittelalterliche Schreibpraxis behielt meist die Beschränkung auf die sieben ersten Zeichen bei und kannte auch noch die Überstreichung zumindest als Option zur Vertausendfachung des Zeichenwertes, während die Schreibung mit Rahmen nicht fortgesetzt wurde. Sie verwendete seit dem Ausgang des Frühmittelalters aber vielfach auch im engeren Sinn multiplikative Schreibweisen, bei denen, anders als im Stil der Kaiserzeit, kumulative Ausdrücke multiplikativ miteinander verknüpft wurden, hauptsächlich zur Vervielfachung der Zeichenwerte 100 und 1000 nach dem Prinzip IVc (statt CCCC oder CD) = 4 × 100, oder III.M (statt MMM oder III) = 3 × 1000, oder C^m (statt ↈ oder I oder C) für centies mille = 100 × 1000, okkasionell aber auch als alternativ mögliche Schreibweise niedrigerer Zahlen wie z.B. IIIIxx et huit (4 × 20 + 8, statt LXXXVIII) für 88. Weil die Überstreichung im abazistischen Schrifttum zeitweise sowohl zur Vertausendfachung des Zeichenwertes als auch zur Unterscheidung multiplikativer gegenüber kumulativer Zeichenverwendung gebraucht wurde, ergaben sich hierbei oft mehrdeutige Ausdrücke wie xm = 10 × 1000 = 10⁴ (statt 10 × 1000 + 1000 × 1000), oder sogar im = (1 × 1000) × 1000 = 10⁶ (statt 1 × 1000 + 1000 × 1000) und imi ((1 × 1000) × 1000) × (1 × 1000) = 10⁹, deren Bedeutung nur auch dem Kontext zu erschließen war.

Im Ergebnis wandelte sich die römische Zahlschrift zu einem Hybridsystem mit vorwiegend kumulativ-additiver und optional multiplikativ-additiver Zahlenschreibung, wobei die letztere besonders durch den Verzicht auf eigene Potenzwert- und Halbzeichen > 1000 erforderlich wurde. Vereinzelte Tendenzen, kumulativ gebildete Ausdrücke durch Ligatur zu beziffernden Eigenzeichen zusammenzuziehen, wie es besonders für die Schreibung von 40 durch ein aus Ligatur von XL entstandenes geschweiftes X bekannt ist, haben sich demgegenüber nicht durchgesetzt.

Griechisch

Griechische Myriadenschreibweise nach Pappos
	1	2	3	4	5	6	7	8	9
100	α	β	γ	δ	ε	ϝ]	ζ	η	Θ θ
101	ι	κ	λ	μ	ν	ξ	ο	π	ϙ
102	ρ	σ	τ	υ	φ	χ	ψ	ω	ϡ
103	,α	,β	,γ	,δ	,ε	,ϝ	,ζ	,η	,θ
104	Μαα	Μαβ	Μαγ	Μαδ	Μαε	Μαϝ	Μαζ	Μαη	Μαθ
105	Μαι	Μακ	Μαλ	Μαμ	Μαν	Μαξ	Μαο	Μαπ	Μαϙ
106	Μαρ	Μασ	Ματ	Μαυ	Μαφ	Μαχ	Μαψ	Μαω	Μαϡ
107	Μα,α	Μα,β	Μα,γ	Μα,δ	Μα,ε	Μα,ϝ	Μα,ζ	Μα,η	Μα,θ
108	Mβα	Μββ	Μβγ	Μβδ	Μβε	Μβϝ	Μβζ	Μβη	Μβθ
usw. mit Μγα = 1012, Μδα = 1016, Μεα = 1020...

In der griechisch-milesischen Zahlschrift war das beziffernd-additive Prinzip durch den Umfang des Alphabets und seiner archaischen Sonderzeichen zunächst auf die ersten drei Potenzen der 10 und damit auf die Zahlen 1 bis 999 beschränkt. Um auch die vierte Potenz, die 10³ (1000er), für Schreibung der Zahlen 1000 bis 9.999 einbeziehen zu können, wurde das System schon früh in der Weise erweitert, daß die Zeichen für 1 bis 9 (Alpha bis Theta) durch den Zusatz eines komma-ähnlichen diakritischen Zeichens in ihrem Wert vertausendfacht wurden. Auch hier kann man, wie bei der Überstreichung der römischen Zahlzeichen, den Strukturtyp einerseits einfach nur als Fortsetzung des beziffernd-additiven Grundprinzips mit einer diakritisch abgeleiteten vierten Zeichenreihe, andererseits aber auch als multiplikative Erweiterung für die Schreibung von Zahlen > 999 deuten.

Die ersten vier Potenzen der 10 bildeten in der griechichischen Zahlentheorie eine ‚Tetrade‘, eine Vierheit, in der die ‚Monaden‘, die Grundeinheiten des Zahlensystems, auf der Basis 10 gezählt wurden, während die fünfte Potenz, 10⁴ (10.000er), ‚Myriade‘ genannt und zahlwörtlich und zahlschriftlich als eine Art übergeordnete Basis eingesetzt wurde, um auch Zahlen ≥ 10.000 auszudrücken. Zahlschriftlich wurde dies in der mathematischen Literatur mit einem akrophonisch aus dem Wort μυριάς (Myriade) abgeleiteten Zeichen Μ oder Μυ oder auch mit einer Punktierung alphanumerischer Zeichen bewerkstelligt, hauptsächlich drei Schreibweisen sind hierfür bekannt:

• Das Μ wird unter oder hinter einen alphanumerischen Teilausdruck geschrieben, der die Häufigkeit des Potenzwertes 10⁴ angibt, z.B. bei Aristarch von Samos:

$\textstyle {\overset {,\zeta \rho \mathrm {o} \epsilon }{\mathrm {M} }}\ ,\!\epsilon \omega \mathrm {o} \epsilon$
= (7000 + 100 + 70 + 5) × 10.000 + 5000 + 800 + 70 + 5 = 7175'5875 = 71.755.875

• Das Μ wird vor den alphanumerischen Wert gesetzt und dieser als Zählung der Miriaden durch einen Punkt von der Zählung der ‚Monaden‘ (1 bis 9.999) abgesetzt, z.B. bei Diophant von Alexandria:

$\textstyle {\overset {\Upsilon }{\mathrm {M} }}\ \rho \nu \ .\ ,\!\zeta \mathrm {\sampi} \pi \delta$
= (100 + 50) × 10.000 + 7000 + 900 + 80 + 4 = 150'7984 = 1.507.984

• Das alphanumerische Zeichen, das die Anzahl der Myriaden angibt, wird diakritisch mit einem Trema (¨) überschrieben, z.B. bei Heron von Alexandria:

$\textstyle {\overset {..}{\alpha }},\!\eta \phi \mathrm {\coppa} \beta$
= 18.592

Für noch größere Zahlen wurde die Myriade nicht nur mit niedrigeren Zahlen bis 9.999 vervielfacht, sondern auch mit sich selbst potenziert, wofür zwei Schreibweisen bekannt sind:

• Das Μ wird mit einem alphanumerischen Zeichen überschrieben, das den Wert des Exponenten ausdrückt. Pappos von Alexandria verwendet diese Schreibweise in den Multiplikationstabellen des zweiten Buches seiner mathematischen Sammlungen, Beispiel:

Μ^δ ιθ καὶ Μ^γ ,ϝλϝ καὶ Μ^β ,ηυπ
= 19 [mal] 10.000⁴ und 6036 [mal] 10.000³ und 8480 10.000² = 19'6036'8480'0000'0000 = 196.036.848.000.000.000

• Ein alphanumerisches Zeichen, das die Häufigkeit der betreffenden Potenz von 10.000 zählt, wird in Weiterentwicklung der heronischen Schreibweise mit so vielen Tremata überschrieben, wie es dem Wert des Exponenten dieser Potenz entspricht, so in einem der beiden arithemtischen Briefe des byzantinischen Mathematikers Nikolaos Rhabdas (um 1342), Beispiel:

$\textstyle {\overset {::}{\iota \beta }}\ {\overset {..}{,\!\sigma }}{\overset {..}{\psi }}{\overset {..}{\mu }}{\overset {..}{\eta }}\omega$
= 12'6745'0800 = 1.267.450.800

Im Ergebnis entstand ein Hybridsystem additiven Typs, in dem die Zahlen bis zum dritten Potenzbereich (10²) beziffernd-additiv, die Zahlen des vierten Potenzbereichs (10³) je nach Betrachtung des Strukturtyps weiterhin beziffernd-additiv oder diakritisch multiplikativ und die Myriaden schließlich (≥ 10⁴) entweder mit einem Myriadenzeichen multiplikativ oder mit heronischen Punktierungen nach dem gleichen Prinzip wie der vorhergehende Potenzbereich geschrieben werden konnten. Auch hier konvergierte die Myriadenschreibweise zumindest in der Tendenz einem übergreifend positionellen System auf der Basis 10⁴, da sie beziffernd-additiv (oder diakritisch multiplikativ) gebildete Teilausdrücke nach Tetraden sortierte, sie hierbei aber im Unterschied zu einem echten positionellen System immer noch mit einem multiplikativen Potenzwertzeichen unterschied (wenn nicht, wie bei Heron und Nikolaos Rhabdas, das alphanumerische Zeichen stattdessen potenzierend punktiert wurde).

Literatur

Zahlwörter

• Václav Blažek: Numerals. Comparative-etymological analyses of numeral systems and their implications, Brünn: Masarykova Univerzita, 1999
• Bernard Comrie: Some problems in the theory and typology of numeral systems, in: Bohumil Palek (Hrsg.), Typology: prototypes, item orderings and universals. Proceedings of LP'96, Prag: Karolinum (= Acta Universitatis Carolinae, Philologica, 1997, 3/4), S. 41-56
• Bernard Comrie: Numeral Bases, in: Matthew S. Dryer / Martin Haspelmath, The World Atlas of Language Structures Online, München: Max Planck Digital Library, 2011, Kap. 131: Online-Version
• Michael A. B. Deakin: The name of the number, Camberwell: ACER Press, 2007 (= The Emergence of Number, 3), ISBN 978-0-86431-757-5
• James A. Hurford: Language and Number. The Emergence of a Cognitive System, Oxford / Cambridge (Mass.): Blackwell, 1987, Nachdruck 1990, ISBN 0-631-15568-6
• Heike Wiese: Numbers, Language, and the Human Mind, Cambridge [u.a.]: Cambridge University Press, 2003, ISBN 978-0-521-83182-6

Zahlschrift

• Stephen Chrisomalis: Numerical Notation. A Comparative History, Cambridge [u.a.]: Cambridge University Press, 2010, ISBN 978-0-521-87818-0
• Geneviève Guitel: Histoire comparée des numérations écrites, Paris: Flammarion, 1975
• Georges Ifrah: Histoire universelle des chiffres, 2. erw. Ausgabe, Paris: Éditions Robert Laffont, 1994, ISBN 2-221-07838-1; deutsche Übersetzung der wesentlich kürzeren 1. Ausgabe von 1981: Universalgeschichte der Zahlen, Frankfurt / New York: Campus, 1991, ISBN 3-88059-956-4
• Karl Menninger: Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl, 2., neubearbeitete und erweiterte Auflage, Göttingen: Vandenhoeck & Ruprecht, 1958, Nachdruck ebenda 1998, ISBN 3-525-40701-7