Rhomboeder
Ein Rhomboeder ist ein Polyeder, das von 6 Rauten begrenzt ist. Es ist ein Parallelepiped mit gleich langen Kanten und 3 gleichen Innenwinkeln an zwei gegenüber liegenden Ecken.
Formeln[Bearbeiten | Quelltext bearbeiten]
| Größen eines Rhomboeders mit der Kantenlänge a und dem Innenwinkel | ||
|---|---|---|
| Volumen | 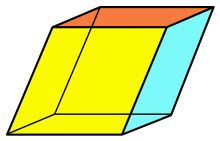
| |
| Oberflächeninhalt | ||
| Inkugelradius | ||
| Höhe | ||
| Raumdiagonalen[1] | ||
| Flächendiagonalen | ||
| Verhältnis von Inkugelvolumen zu Volumen | ||
| Winkel zwischen
benachbarten Flächen |
||
| Raumwinkel in den Ecken | ||
Volumen[Bearbeiten | Quelltext bearbeiten]
Das Volumen des Rhomboeders kann mithilfe der Formel für das Volumen des Parallelepipeds berechnet werden (siehe Parallelepiped - Volumen). Für das Rhomboeder sind alle Kanten gleich lang und die 3 Innenwinkel zwischen den Kanten gleich, also gilt und . Daraus ergibt sich das Volumen
Flächenwinkel[Bearbeiten | Quelltext bearbeiten]
Für zwei gegenüber liegenden Ecken des Rhomboeders sind die 3 anliegenden Innenwinkel der rautenförmigen Seitenflächen gleich. Eine solche Ecke bildet zusammen mit den 3 benachbarten Ecken ein Tetraeder. Betrachtet man die Umkugel dieses Tetraeders, dann gilt nach dem Kosinussatz für Kugeldreiecke die Gleichung
Dabei sind die Innenwinkel und die Flächenwinkel zwischen diesen Seitenflächen.
Daraus folgt
Für die sechs anderen Ecken des Rhomboeders sind die anliegenden Innenwinkel gleich , und . Betrachtet man die Umkugel des entsprechenden Tetraeders, dann gilt nach dem Kosinussatz für Kugeldreiecke die Gleichung
Dabei sind die Flächenwinkel zwischen den Seitenflächen mit den Innenwinkeln und .
Daraus folgt
Raumwinkel[Bearbeiten | Quelltext bearbeiten]
Der Raumwinkel in der Ecke eines Polyeders kann mit dem Satz von L'Huilier berechnet werden.[4]
Für die zwei gegenüber liegenden Ecken des Rhomboeders mit den 3 gleichen Innenwinkeln ergibt sich der Raumwinkel
weil in diesem Fall ist.
Für die sechs anderen Ecken mit den anliegenden Innenwinkeln , und ergibt sich der Raumwinkel
wobei in diesem Fall ist.
Raumfüllung mit Rhomboedern[Bearbeiten | Quelltext bearbeiten]
Der dreidimensionale euklidische Raum kann lückenlos mit kongruenten Rhomboedern ausgefüllt werden. Solche dreidimensionalen Parkettierungen werden Raumfüllung genannt.
Diese Raumfüllung aus Rhomboedern bildet ein Gitter. Es entspricht dem trigonalen Kristallsystem in der Kristallographie.
Dieses Gitter enthält parallele Ebenen. Deshalb ergeben die Flächenwinkel und zusammen 180°. Die im Gitter benachbarten Raumwinkel und entsprechen zusammen dem Flächenwinkel . Der volle Flächenwinkel beträgt und der volle Raumwinkel beträgt . Daher gilt .
Außerdem sind im Gitter 2 gleiche Raumwinkel benachbart und entsprechen zusammen dem Flächenwinkel . Daher gilt .
Anwendungen[Bearbeiten | Quelltext bearbeiten]


Kunst und Natur[Bearbeiten | Quelltext bearbeiten]
- Albrecht Dürer stellt in seiner teils mathematisch inspirierten Grafik Melencolia I ein speziell beschnittenes Rhomboeder dar, das durch diese Modifikation mit all seinen Eckpunkten auf einer Kugelfläche liegen würde.
- Maurits Cornelis Escher nutzte bei seinen unmöglichen Figuren bei Vorbetrachtungen und Strukturentwicklung auch verschiedene Rhomboeder.
Kristallographie[Bearbeiten | Quelltext bearbeiten]
Das Rhomboeder findet sich in der Natur als Kristallform und auf atomarer Ebene in Kristallstrukturen wieder. Es ist die allgemeine Flächenform der rhomboedrischen Kristallklasse (3), eine Grenzform der trigonal-trapezoedrischen (32) und eine spezielle Form der ditrigonal-skalenoedrischen Kristallklasse (3m). Außerdem ist es die Grundform des rhomboedrischen Bravais-Gitters. Das Rhomboeder als Kristallform gibt es nur im trigonalen Kristallsystem.
Zum Beispiel kristallisieren die Mineralien Amethyst, Hämatit, Calcit und Dolomit im trigonalen Kristallsystem.
Das Farben-Rhomboeder[Bearbeiten | Quelltext bearbeiten]
Das Farben-Rhomboeder erfüllt nach Harald Küppers die geometrische Lösung für seine Farbenlehre. Jeder Punkt innerhalb des geometrischen Körpers entspricht einer Farbvalenz. Das heißt, jeder dieser Farbpunkte ist durch seine drei Vektoren-Potentiale definiert.[9] Durch Stauchung und Verzerrung lässt sich das Farben-Rhomboeder in einen RGB- oder einen CYM-Farbraum umwandeln, naturgemäß mit anderen Verhältnissen zwischen den Farbwerten.
Ein Rhomboeder, bei dem die kurze Diagonale der Außenflächen so lang wie die Kante des Rhomboeders ist, stellt ein symmetrisches Parallelepiped dar. Es stehen jeweils zwei Außenflächen einander parallel gegenüber. Jede rautenförmige Außenfläche besteht aus zwei gleichseitigen Dreiecken. Zerschneidet man ein Rhomboeder entlang der kurzen Diagonalen der Außenflächen, ergeben sich drei Teile: zwei Tetraeder und ein Oktaeder. Diese drei geometrischen Körper sind wiederum völlig symmetrisch. Sämtliche Außenflächen dieser drei neuen geometrischen Körper sind gleichseitige Dreiecke.
- Küppers' Farbrhomboeder
-
Farbkörper nach Harald Küppers
-
Anmerkenswerte Schnitte
-
Achsen, Diagonalen und Kanten[10]
Siehe auch[Bearbeiten | Quelltext bearbeiten]
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Blauer Calcit Rhomboeder
- Rhombenkörper
- Eric W. Weisstein: Rhomboeder. In: MathWorld (englisch).
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Stack Exchange: Formula for length of the diagonal of a parallelepiped
- ↑ Stack Exchange: Dihedral angles between tetrahedron faces from triangles' angles at the tip
- ↑ G. Richardson: The Trigonometry of the Tetrahedron. In: The Mathematical Gazette. 2. Jahrgang, Nr. 32, 1. März 1902, S. 149–158, doi:10.2307/3603090 (zenodo.org).
- ↑ Wolfram MathWorld: Spherical Excess
- ↑ aus Augsburg Naturmuseum, gefunden Goslerwand, Osttirol
- ↑ Museo civico di storia naturale a Milano, Fundort Kasachstan
- ↑ Fundort China: rhombeoedrischer gelber transparenter Kristall: Calcite jaune
- ↑ Illustration aus Encyclopædia Britannica (1911), article CALCITE.
- ↑ Küppers' Farbenlehre ( vom 26. Januar 2012 im Internet Archive)
- ↑ W: weiß, S: schwarz, N: Neutralgrau, B→M→R→Y→G→C: sechs Buntfarben (blau, magenta, rot, gelb, grün, cyan)





































![Calcit[5]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/00/Calcite_3.jpg/187px-Calcite_3.jpg)
![Calcit-Kristall[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/db/9106_-_Milano_-_Museo_storia_naturale_-_Calcite_-_Foto_Giovanni_Dall%27Orto_22-Apr-2007.jpg/167px-9106_-_Milano_-_Museo_storia_naturale_-_Calcite_-_Foto_Giovanni_Dall%27Orto_22-Apr-2007.jpg)
![Gelber Calcit[7]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/eb/Calcite_jaune_%28Chine%29.jpg/271px-Calcite_jaune_%28Chine%29.jpg)
![Rhomboedrische Kristalle[8]](http://upload.wikimedia.org/wikipedia/commons/thumb/5/57/Calcite_1_6.png/244px-Calcite_1_6.png)


![Achsen, Diagonalen und Kanten[10]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/19/Rhomboeder-Neutralgrau.svg/87px-Rhomboeder-Neutralgrau.svg.png)