Stammbaum (Gruppentheorie)
In der algorithmischen Gruppentheorie versteht man unter einem Stammbaum einen gerichteten Baum zur Modellierung von sogenannten Vorgänger-Nachfolger-Relationen zwischen Isomorphieklassen endlicher p-Gruppen. Letztere sind endliche Gruppen mit einer Primzahlpotenz als Ordnung. Die Basis ist dabei eine feste Primzahl und der Exponent ist eine positive ganze Zahl. Die Knoten (auch Ecken oder Vertices genannt) des Stammbaums sind Isomorphieklassen endlicher -Gruppen. Die Kanten des Baums verbinden genau jene Paare von Knoten, die in der Vorgänger-Nachfolger-Beziehung stehen.
Eine endliche -Gruppe besitzt neben der Ordnung zwei weitere Invarianten, die Nilpotenzklasse (kurz Klasse) und die Koklasse . Es stellte sich heraus, dass gewisse Klassen von Stammbäumen, die sogenannten bereinigten oder gestutzten Koklassen-Bäume, deren unendlich viele Vertices eine gemeinsame Koklasse besitzen, ein sich periodisch wiederholendes endliches Muster aufweisen. Diese zwei entscheidenden Eigenschaften der Endlichkeit und Periodizität, die von M. du Sautoy[1] und unabhängig von B. Eick und C. R. Leedham-Green[2] bewiesen wurden, gestatten eine Charakterisierung sämtlicher Mitglieder des Baumes durch endlich viele parametrisierte Präsentationen. Folglich spielen Stammbäume eine fundamentale Rolle in der Klassifikation endlicher -Gruppen.
Mit Hilfe der Kerne und Ziele der Artinschen Verlagerungs-Homomorphismen können Stammbäume mit zusätzlicher Struktur ausgestattet werden, die neulich zu unerwarteten Erfolgen bei arithmetischen Anwendungen in der Klassenkörpertheorie führte, insbesondere bei der Bestimmung der exakten Länge von Klassenkörpertürmen[3].
Ein Stammbaum kann mit Hilfe des -Gruppen-Erzeugungs-Algorithmus (pGEA) konstruiert werden, ausgehend von einer vorgegebenen Anfangsgruppe, die als Wurzel des Baums angenommen wird. Der pGEA ist ein rekursiver Prozess für die Lösung dieses Problems der Konstruktion des Stammbaums einer gegebenen endlichen -Gruppe, welche die Wurzel des Baums bildet. Dieser Algorithmus ist im Softwarepaket ANUPQ (Australian National University P-Quotient)[4] der Computer-Algebra-Systeme GAP (Groups-Algorithms-Programming) und Magma implementiert.
Definitionen und Terminologie[Bearbeiten | Quelltext bearbeiten]
Wir definieren eine Baumstruktur und starten mit einer endlichen -Gruppe .
Vorgänger und Nachfolger[Bearbeiten | Quelltext bearbeiten]
Vorgänger[Bearbeiten | Quelltext bearbeiten]
Es gibt mehrere unterschiedliche Definitionen des (unmittelbaren) Vorgängers einer endlichen -Gruppe . Das gemeinsame Prinzip ist die Bildung des Quotienten von nach einem geeigneten Normalteiler , für den es die folgenden Möglichkeiten gibt:[5]
- V
- das Zentrum von , in welchem Fall der Zentralquotient von genannt wird (V1),
- der letzte nicht-triviale Term der absteigenden Zentralreihe von , wobei die Nilpotenzklasse von bezeichnet (V2),
- der letzte nicht-triviale Term der unteren Exponent-p-Zentralreihe von , wobei die Exponent-p-Klasse von bedeutet (V3),
- der letzte nicht-triviale Term der abgeleiteten Reihe von , wobei die abgeleitete Länge von bezeichnet (V4).
Nachfolger[Bearbeiten | Quelltext bearbeiten]
In jedem dieser Fälle heißt ein unmittelbarer Nachfolger von und eine gerichtete Kante des Baums wird erklärt entweder als in Richtung der kanonischen Projektion auf den Quotienten oder als in der entgegengesetzten Richtung, die für Stammbäume geläufiger ist.
Die erstere Konvention (sogenannter In-Tree) wird verwendet von C. R. Leedham-Green und M. F. Newman,[6] von M. du Sautoy und D. Segal,[7] von C. R. Leedham-Green und S. McKay,[8] sowie von B. Eick, C. R. Leedham-Green, M. F. Newman und E. A. O'Brien.[9] Die letztere Definition (sogenannter Out-Tree) findet man bei M. F. Newman,[5] bei M. F. Newman und E. A. O'Brien,[10] bei M. du Sautoy,[1] sowie bei B. Eick und C. R. Leedham-Green.[2]
Im Folgenden wird die Richtung der kanonischen Projektionen für alle Kanten gewählt, sodass Stammbäume als gewurzelte In-Trees erscheinen. Dann ist ein Vertex , in Verallgemeinerung des unmittelbaren Nachfolgers, ein Nachfolger eines Vertex , und ist ein Vorgänger von , wenn entweder mit übereinstimmt oder wenn es einen Pfad gibt,
- , wobei ,
bestehend aus gerichteten Kanten von bis zu . Die den Pfad bildenden Vertices fallen notwendigerweise zusammen mit den iterierten Vorgängern von , mit :
- , wobei .
Erläuterungen[Bearbeiten | Quelltext bearbeiten]
Definition V2[Bearbeiten | Quelltext bearbeiten]
Im einen wichtigen Spezialfall (V2) von Vorgängern, die als Quotienten nach der letzten nicht-trivialen unteren Zentrale definiert sind, können die Vertices des Pfades auch aufgefasst werden als sukzessive Quotienten der Klasse von , falls die Nilpotenzklasse von durch gegeben ist:
- , mit .
Definition V3[Bearbeiten | Quelltext bearbeiten]
Im anderen wichtigen Spezialfall (V3) von Vorgängern, die als Quotienten nach der letzten nicht-trivialen unteren Exponent-p Zentrale definiert sind, können die Vertices des Pfades auch aufgefasst werden als sukzessive Quotienten der p-Klasse von , falls die p-Klasse von durch gegeben ist:
- , mit .
Stammbaum[Bearbeiten | Quelltext bearbeiten]
Allgemein ist der Stammbaum eines Vertex der Teilbaum aller Nachfolger von , beginnend an der Wurzel . Der maximal mögliche Stammbaum der trivialen Gruppe enthält alle endlichen -Gruppen und ist sehr exzeptionell, weil die triviale Gruppe für jede Vorgänger-Definition (V1–V4) unendlich viele abelsche -Gruppen als unmittelbare Nachfolger hat. Dabei ist aber zu beachten, dass die triviale Gruppe nur eine entartete -Gruppe für jede beliebige Primzahl ist.
Der Übergang von einem Vorgänger zu seinen Nachfolgern wird auch Propagation genannt. Äquivalente Sprechweisen dafür, dass Nachfolger von ist, sind: stammt von ab, gibt Anlass zu und propagiert zu .
Weiteres zu V1–V4[Bearbeiten | Quelltext bearbeiten]
Die Vorgänger-Definitionen (V2) und (V3) haben den Vorteil, dass jede nicht-triviale endliche -Gruppe (mit durch teilbarer Ordnung) nur endlich viele unmittelbare Nachfolger besitzt. Bei Verwendung der Definition (V1) des Vorgängers als Zentralquotient kann es vorkommen, dass unendlich viele -Gruppen denselben Vorgänger haben. Für jede ungerade Primzahl besitzen beispielsweise die Gruppen aller abzählbar unendlich vielen Zweige der Isoklinieklassen und von P. Hall[11] dieselbe Gruppe maximaler Klasse als Zentralquotienten . Auch die Definition (V4) des Vorgängers als Quotient nach der letzten nicht-trivialen abgeleiteten Untergruppe hat denselben Nachteil. Beispielsweise ist jede nicht-zyklische abelsche -Gruppe Kommutator-Quotient und somit Vorgänger von unendlich vielen metabelschen -Gruppen , die ja die abgeleitete Länge haben.
Die Definition (V2) des Vorgängers als Quotient nach der letzten nicht-trivialen unteren Zentrale hat den Vorteil, dass der Vorgänger einer nicht-abelschen -Gruppe nicht nur denselben Erzeugenden-Rang , sondern sogar denselben Kommutator-Quotienten, also dieselbe Abelisierung, besitzt wie :
- ,
weil für .

Warnung. Im Hinblick auf den -Gruppen-Erzeugungs-Algorithmus, der die Definition (V3) des Vorgängers als Quotient nach der letzten nicht-trivialen unteren p-Zentrale verwendet, muss darauf hingewiesen werden, dass zwar nach dem Basissatz von Burnside denselben Erzeugenden-Rang besitzt wie , aufgrund der Invarianz des Frattini-Quotienten, also der Elementar-Abelisierung:
- ,
weil für , dass aber eine andere Abelisierung aufweisen kann als , wenn nicht . Man spricht dann von exogenetischer Propagation, bei Invarianz der Abelisierung hingegen von endogenetischer Propagation. Diese Arten der Propagation werden in Abbildung 0 durch Nachkommen mit drei verschiedenen Schrittweiten veranschaulicht, wobei als Wurzel die elementar-bizyklische -Gruppe mit einer beliebigen Primzahl dient.
Pro-p-Gruppen und Koklassen-Bäume[Bearbeiten | Quelltext bearbeiten]
Für ein solides Verständnis von Koklassen-Bäumen als spezielle und besonders bedeutende Instanz von Stammbäumen, ist es erforderlich, einige Tatsachen in Bezug auf unendliche topologische pro--Gruppen zusammenzufassen. Die Terme , mit , der unteren Zentralreihe einer pro- Gruppe sind abgeschlossene (und offene) Untergruppen mit endlichem Index. Daher sind die entsprechenden Quotienten endliche -Gruppen. Man sagt, die pro--Gruppe sei von der Koklasse , wenn der Grenzwert der Koklasse der sukzessiven Quotienten existiert und endlich ist. Eine unendliche pro--Gruppe der Koklasse ist eine -adische prä-Raumgruppe,[9] weil sie einen Normalteiler enthält, die Translationsgruppe, der als freier Modul über dem Ring der -adischen ganzen Zahlen einen eindeutig bestimmten Rang besitzt, die Dimension, sodass der Quotient eine endliche -Gruppe ist, die Punktgruppe, welche auf uniseriell operiert. Die Dimension ist gegeben durch
, mit einer gewissen ganzen Zahl .
Ein zentrales Endlichkeits-Ergebnis für unendliche pro--Gruppen der Koklasse ist enthalten im sogenannten Theorem D, einem der fünf Koklassen-Theoreme die im Jahr 1994 unabhängig bewiesen wurden von A. Shalev[12] und von C. R. Leedham-Green,[13] und die bereits im Jahr 1980 von C. R. Leedham-Green und M. F. Newman vermutet worden waren.[6] Theorem D garantiert, dass es nur endlich viele Isomorphieklassen unendlicher pro--Gruppen der Koklasse gibt, für jede feste Primzahl und jede feste nicht-negative ganze Zahl . Als Konsequenz existiert zu jeder unendlichen pro--Gruppe der Koklasse eine kleinste ganze Zahl , sodass die folgenden drei Bedingungen für jede ganze Zahl erfüllt werden.
- S
- die Koklasse des unteren Zentralquotienten hat den festen Wert (S1),
- ist nicht unterer Zentralquotient einer anderen unendlichen pro--Gruppe der Koklasse , die nicht isomorph zu ist (S2),
- der Faktor ist zyklisch von der Ordnung (S3).
The Stammbaum , bezüglich der Vorgänger-Definition (V2), der Wurzel mit minimalem heißt der Koklassen-Baum von und sein eindeutig bestimmter maximaler unendlicher (umgekehrt-orientierter) Pfad
wird als Hauptlinie (oder Stamm) des Baumes bezeichnet.

Baum-Diagramm[Bearbeiten | Quelltext bearbeiten]
In Diagrammen zur Visualisierung endlicher Teile von Stammbäumen verwendet man eine Terminologie, die in Abbildung 1 mit Hilfe eines abstrakten Baums erklärt wird. Auf der linken Seite bestimmt ein Niveau das grundlegende Top-Down-Design eines Stammbaums. In konkreten Bäumen, etwa in Abbildung 3, wird das Niveau üblicherweise ersetzt durch eine Skala von Ordnungen, die von Kopf bis Fuß zunehmen. Ein Vertex ist erweiterbar, wenn er zumindest einen unmittelbaren Nachfolger besitzt, anderenfalls ist er terminal (oder ein Blatt). Vertices mit einem gemeinsamen Vorgänger heißen Geschwister.
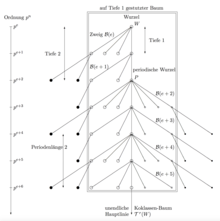
Ist der Stammbaum ein Koklassen-Baum mit fester Koklasse Wurzel und mit Hauptlinie , deren Vertices dem Niveau entsprechend etikettiert sind, dann heißt der endliche Teilbaum, der als Differenz
definiert ist, der -te Zweig des Baums (Branch) oder auch der Zweig mit Wurzel , für jedes . Die Tiefe eines Zweigs ist die maximale Länge der Pfade, die seine Vertices mit seiner Wurzel verbinden. Abbildung 2 zeigt einen abstrakten Koklassen-Baum, dessen Zweige und vorperiodische Unregelmäßigkeiten aufweisen. Alle seine Zweige haben die Tiefe . Die Zweige und sind paarweise isomorph als Graphen, weil die Periodizität (mit Länge ) beim dritten Vertex der Hauptlinie, der periodischen Wurzel , einsetzt. Das Niveau der Ordnungen wird durch Verwendung eines Exponenten variabel belassen.
Wenn alle Vertices mit einer Tiefe oberhalb einer vorgegebenen ganzen Zahl aus dem Zweig entfernt werden, dann erhält man den auf die Tiefe gestutzten Zweig .Dementsprechend besteht der auf die Tiefe gestutzte Koklassen-Baum , beziehungsweise the vollständige Koklassen-Baum , aus der unendlichen Folge seiner gestutzten Zweige , beziehungsweise (vollen) Zweige , verbunden durch die Hauptlinie, deren Vertices als unendlich erweiterbar bezeichnet werden. In der Abbildung 2 ist der auf die Tiefe gestutzte Koklassen-Baum hervorgehoben.
Virtuelle Periodizität[Bearbeiten | Quelltext bearbeiten]
Die Periodizität der Zweige eines gestutzten Koklassen-Baums wurde bewiesen mit analytischen Methoden unter Verwendung von Kegel-Integralen und Zeta-Funktionen[7] von Gruppen durch M. du Sautoy,[1] und mit algebraischen Techniken mittels Kohomologiegruppen durch B. Eick und C. R. Leedham-Green.[2] Die ersteren Methoden gestatten die qualitative Einsicht in die ultimative virtuelle Periodizität, während die letzteren Techniken sogar die quantitative Struktur enthüllen.
Theorem[Bearbeiten | Quelltext bearbeiten]
Für jede unendliche pro--Gruppe der Koklasse und Dimension , und für jede vorgegebene Tiefe , gibt es eine effektive kleinste untere Schranke , ab der die Periodizität der Länge der gestutzten Zweige des Koklassen-Baums einsetzt, das heißt, es existieren Graphen-Isomorphismen
- für alle .
Beweis[Bearbeiten | Quelltext bearbeiten]
Die Graphen-Isomorphismen der auf die Tiefe gestutzten Zweige mit Wurzeln hinreichend großer Ordnung werden mit kohomologischen Methoden hergeleitet in Theorem 6, p. 277, und Theorem 9, p. 278, durch Eick und Leedham-Green.[2] Die effektive untere Schranke für die Ordnungen der Zweigwurzeln wird nachgewiesen in Theorem 29, p. 287, des genannten Artikels. (Ende des Beweises.)
Diese zentralen Resultate lassen sich anschaulich folgendermaßen formulieren: Betrachten wir einen Koklassen-Baum mit einem Paar von Scheuklappen und ignorieren wir eine endliche Anzahl vor-periodischer Zweige an der Spitze, dann werden wir ein sich wiederholendes endliches Muster sehen (ultimative Periodizität beim Abschneiden in fester Tiefe). Wenn wir jedoch immer breitere Scheuklappen verwenden, dann kann der vor-periodische Anfangsabschnitt immer länger werden (virtuelle Periodizität bei variabler Tiefe).
Der Vertex heißt die periodische Wurzel des gestutzten Koklassen-Baums, für einen festen Wert der Tiefe . Siehe Abbildung 2.
Multifurkation und Koklassen-Graphen[Bearbeiten | Quelltext bearbeiten]
Es sei wieder angenommen, die Vorgänger endlicher -Gruppen sind definiert als letzte nicht-triviale untere Zentralquotienten (V2). Für eine -Gruppe mit Koklasse unterscheidet man ihren (vollständigen) Stammbaum und ihren Koklasse- Stammbaum . Letzterer ist der Teilbaum, welcher ausschließlich aus Nachfolgern mit Koklasse besteht. Die Gruppe heißt koklassen-stabil, wenn beide Bäume zusammenfallen, wenn es also keine Nachfolger von mit größerer Koklasse als gibt.
Im Fall der Vorgänger-Definition (V3) (bei der Definition (V2) im Allgemeinen nur für hinreichend große Ordnung) erlaubt der nukleare Rang der Gruppe in der Theorie des -Gruppen-Erzeugungs-Algorithmus von M. F. Newman[14] und E. A. O'Brien[15] die folgenden drei Kriterien.
- N
- ist terminal, und somit trivialerweise koklassen-stabil, genau dann, wenn (N1).
- Falls , dann ist erweiterbar, aber es bleibt zunächst unbekannt, ob koklassen-stabil ist (N2).
- Falls , dann ist erweiterbar und ganz offensichtlich nicht koklassen-stabil (N3).
Im letzten Fall ist eine präzisere Aussage möglich: Hat die Gruppe die Koklasse und den nuklearen Rang , dann gibt sie Anlass zu einer -fachen Multifurkation in einen regulären Koklasse- Stammbaum und irreguläre Graphen der Koklasse , mit . Folglich ist der Stammbaum von die disjunkte Vereinigung
- .
Multifurkation korreliert mit verschiedenen Ordnungen der letzten nicht-trivialen unteren Zentrale von unmittelbaren Nachfolgern. Da die Nilpotenzklasse beim Übergang von einem Vorgänger zu jedem unmittelbaren Nachfolger exakt um eine Einheit zunimmt, , bleibt die Koklasse genau dann stabil, , wenn the letzte nicht-triviale untere Zentrale zyklisch von der Ordnung ist. Dann nimmt nämlich der Exponent der Ordnung ebenfalls exakt um eine Einheit zu, . In diesem Fall ist ein regulärer unmittelbarer Nachfolger mit gerichteter Kante der Schrittweite , wie üblich. Die Koklasse nimmt jedoch um zu, wenn eine höhere Ordnung mit besitzt. Dann ist ein irregulärer unmittelbarer Nachfolger mit gerichteter Kante der Schrittweite .
Wenn allen gerichteten Kanten die Bedingung der Schrittweite auferlegt wird, dann zerfällt der maximale Stammbaum der trivialen Gruppe in eine abzählbar unendliche disjunkte Vereinigung
von gerichteten Koklassen-Graphen , die im Allgemeinen eher Wälder sind als Bäume. In breiterer Ausführlichkeit formuliert, implizieren die oben-erwähnten Koklassen-Theoreme, dass
eine disjunkte Vereinigung ist, einerseits von endlich vielen Koklassen-Bäumen mit assoziierten paarweise nicht-isomorphen unendlichen pro--Gruppen der Koklasse (Theorem D) und andererseits von einem endlichen Teilgraphen von sporadischen Gruppen, die außerhalb von jeglichen Koklassen-Bäumen liegen.
Identifier[Bearbeiten | Quelltext bearbeiten]
Die SmallGroups Library Identifier von beliebigen endlichen Gruppen, insbesondere auch von endlichen -Gruppen, die in den folgenden konkreten Beispielen von Stammbäumen in der Gestalt
angegeben werden, stammen von H. U. Besche, B. Eick and E. A. O'Brien.[16][17] Sind die Gruppen-Ordnungen längs einer Skala auf der linken Seite angeordnet, wie in den Abbildungen 3 und 4, dann werden die Identifier kurz in Winkel-Klammern notiert als
.
Abhängig von der Primzahl gibt es eine obere Schranke der Ordnung von Gruppen, für die ein SmallGroup Identifier existiert, zum Beispiel für , für und für . Für Gruppen mit größeren Ordnungen wird eine Notation mit relativen Identifiern verwendet, welche die Nachfolger-Struktur imitiert. Ein regulärer unmittelbarer Nachfolger, der durch eine Kante der Schrittweite mit seinem Vorgänger verbunden ist, wird bezeichnet mit
,
und ein irregulärer unmittelbarer Nachfolger, von dem aus eine Kante der Schrittweite zu seinem Vorgänger führt, wird notiert in der Gestalt
.
Die Implementierungen des -Gruppen Erzeugungs-Algorithmus in den Computational Algebra Systemen GAP (Groups, Algorithms, Programming) und Magma benützen diese relativen Identifier, die auf J. A. Ascione im Jahr 1979 zurückgehen.[18]
Konkrete Beispiele von Stammbäumen[Bearbeiten | Quelltext bearbeiten]
In allen Beispielen bezieht sich die zugrundeliegende Vorgänger-Definition (P2) auf die gewöhnliche untere Zentralreihe. Gelegentliche Unterschiede zur Vorgänger-Definition (P3) in Bezug auf die untere Exponent-p Zentralreihe werden besonders hervorgehoben.
Koklasse 0[Bearbeiten | Quelltext bearbeiten]
Der Koklassen-Graph der endlichen -Gruppen mit Koklasse enthält keinerlei Koklassen-Bäume, sondern besteht ausschließlich aus sporadischen Gruppen,
- ,
nämlich aus der trivialen Gruppe und der zyklischen Gruppe der Ordnung , die in Bezug auf die Vorgänger-Definition (V2) terminal ist. (Sie ist jedoch erweiterbar bezüglich der Definition (V3) mit der unteren Exponent-p Zentralreihe und gibt Anlass zu der separaten exogenetischen Propagation sämtlicher zyklischen -Gruppen mit ). Für ist der SmallGroup Identifier von , für ist er .
Koklasse 1[Bearbeiten | Quelltext bearbeiten]
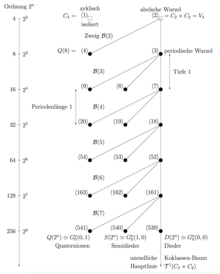
Der Koklassen-Graph aller endlichen -Gruppen der Koklasse , die auch als Gruppen maximaler Klasse bezeichnet werden,
- ,
besteht aus einem einzigen Koklassen-Baum mit Wurzel , der elementar abelschen -Gruppe vom Rang , und einem einzelnen isolierten Vertex (einem terminalen Waisenkind ohne echten Vorgänger im selben Koklassen-Graphen, weil die gerichtete Kante zu der trivialen Gruppe die Schrittweite besitzt), der zyklischen Gruppe der Ordnung in the sporadischen Teil . (Wie schon oben erwähnt, ist diese Gruppe jedoch erweiterbar in Bezug auf die untere Exponent-p Zentralreihe.) Der Baum ist der Koklassen-Baum der eindeutig bestimmten unendlichen pro-p Gruppe mit Koklasse .
Für , beziehungsweise , ist der SmallGroup Identifier der Wurzel definiert als , beziehungsweise . Ein Baumdiagramm des Koklassen-Graphen, beginnend mit Zweig bis hinunter zum Zweig (gezählt bezüglich des p-Logarithmus der Ordnung der Zweigwurzel), ist dargestellt in Abbildung 3, beziehungsweise Abbildung 4, wo alle Gruppen der Ordnung zumindest metabelsch sind, also nicht-abelsch mit auflösbarer Länge . Metabelsche Vertices sind durch schwarze Kreisscheiben repräsentiert, im Gegensatz zu Kontur-Quadraten, die abelsche Gruppen symbolisieren. In Abbildung 4 bezeichnen kleinere schwarze Kreisscheiben solche metabelschen 3-Gruppen, deren sämtliche maximalen Untergruppen nicht-abelsch sind, ein neues Phänomen, welches für die metabelschen 2-Gruppen in Abbildung 3 noch nicht auftritt, weil sie alle eine abelsche Untergruppe vom Index besitzen (üblicherweise genau eine). Der Koklassen-Baum im Graphen , beziehungsweise , hat die periodische Wurzel und Periodizität der Länge , beginnend mit Zweig , beziehungsweise die periodische Wurzel , also Periodizität der Länge setzt hier erst mit Zweig ein. Beide Bäume besitzen Zweige global beschränkter Tiefe , sodass also ihre virtuelle Periodizität tatsächlich sogar eine strenge Periodizität ist.
Wesentlich komplexer ist die Struktur des (einzigen) Koklassen-Baums im Graphen mit , denn dieser hat unbeschränkte Tiefe und enthält auch nicht-metabelsche Gruppen. Jeder Baum mit hat sogar unbeschränkte Breite, das heißt, die Anzahl der Nachfolger einer festen Ordnung nimmt mit wachsender Ordnung unbeschränkt zu.[19]
Mit Hilfe der Kerne und Ziele von Artin-Verlagerungen können die Diagramme in den Abbildungen 2 und 3 mit zusätzlicher Information bereichert und als strukturierte Stammbäume dargestellt werden.
Die konkreten Prototypen und von Koklassen-Graphen bieten die Gelegenheit, eine parametrisierte polyzyklische Potenz-Kommutator Präsentation[20] für den vollständigen Koklassen-Baum , , anzugeben. Auf diese Kompression unbeschränkter Informationen über unendlich viele Gruppen in eine endliche Formel wurde bereits in the Einleitung als großer Vorteil des Stammbaum-Konzepts und als Folge der Periodizität des gesamten Koklassen-Baums hingewiesen. In beiden Fällen werden die Gruppen von zwei Elementen erzeugt, aber die Präsentation enthält zusätzlich eine Reihe von höheren Kommutatoren , , die mit dem Hauptkommutator beginnt. Die Nilpotenz wird formal durch die Relation ausgedrückt, wenn die Gruppe von der Ordnung ist.

Für gibt es zwei Parameter und die pc-Präsentation ist gegeben durch
Die 2-Gruppen maximaler Klasse, das heißt von Koklasse , bilden drei periodische unendliche Folgen,
- Diedergruppen, , , welche die Hauptlinie bilden (mit unendlich erweiterbaren Vertices),
- Verallgemeinerte Quaternionengruppen, , , welche sämtlich terminale Vertices sind,
- Semidiedergruppen, , , welche ebenfalls Blätter sind.
Für braucht man drei Parameter, und , und die PC-Präsentation ist gegeben durch
Die 3-Gruppen mit Parameter besitzen eine abelsche maximale Untergruppe, jene mit Parameter haben keine. Genauer ausgedrückt ist eine existierende abelsche maximale Untergruppe eindeutig bestimmt, mit Ausnahme der zwei extra-speziellen Gruppen and , bei denen alle vier maximalen Untergruppen abelsch sind.
Im Gegensatz zu jeder größeren Koklasse enthält der Koklassen-Graph ausschließlich -Gruppen mit Kommutator-Quotient des Typs , mit Ausnahme seines einzigen isolierten Vertex . Der Fall ist ausgezeichnet durch die Gültigkeit der umgekehrten Aussage: Jede beliebige 2-Gruppe mit Abelisierung des Typs ist von der Koklasse (Theorem von O. Taussky[21]).
Koklasse 2[Bearbeiten | Quelltext bearbeiten]
Die Genese des Koklassen-Graphen mit ist nicht uniform, weil -Gruppen mit mehreren verschiedenen Abelisierungen zu seiner Konstitution beitragen. Für die Koklasse hat man essentielle Beiträge durch Gruppen mit Abelisierungen der Typen , , , und einen isolierten Beitrag von der zyklischen Gruppe der Ordnung :
- .
Kommutator-Quotient vom Typ (p,p)[Bearbeiten | Quelltext bearbeiten]
Im Gegensatz zu -Gruppen der Koklasse mit Kommutator-Quotienten vom Typ oder , die als reguläre Nachfolger abelscher -Gruppen desselben Typs zu finden sind, entstehen -Gruppen der Koklasse mit Kommutator-Quotient des Typs als irreguläre Nachfolger einer nicht-abelschen -Gruppe der Koklasse , welche noch nicht koklassen-stabil ist.
Für die Primzahl gibt es überhaupt keine solchen Gruppen, weil die diedrale 2-Gruppe bereits koklassen-stabil ist. Genau das ist die tiefere Ursache für das vielzitierte Taussky-Theorem. Diese bemerkenswerte Tatsache war aber Giuseppe Bagnera[22] schon im Jahr 1898 bewusst.
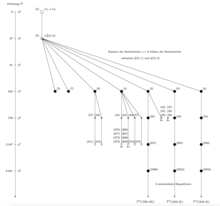
Für alle ungeraden Primzahlen ist die Existenz von -Gruppen mit Koklasse und Kommutator-Quotient des Typs dem Umstand zuzuschreiben, dass die Gruppe noch nicht koklassen-stabil ist. Ihr nuklearer Rang ist und das gibt Anlass zu einer Bifurkation des Stammbaums in zwei Koklassen-Graphen. Die reguläre Komponente ist ein Teilbaum des einzigen Baums im Koklassen-Graphen . Die irreguläre Komponente wird zu einem Teilgraphen des Koklassen-Graphen , wenn die verbindenden Kanten der Schrittweite zu den irregulären unmittelbaren Nachfolgern von entfernt werden.
Für ist dieser Teilgraph in Abbildung 5 dargestellt. Sie zeigt die Schnittstelle zwischen endlichen 3-Gruppen mit Koklasse beziehungsweise und Kommutator-Quotient vom Typ . Der Teilgraph hat sieben Vertices von drei charakteristischen Sorten auf Top-Niveau, alle von der Ordnung , also bereits von G. Bagnera entdeckt.[22]
- Erstens gibt es zwei terminale Schur σ-Gruppen und im sporadischen Anteil des Koklassen-Graphen .
- Zweitens sind die zwei Gruppen und Wurzeln endlicher Bäume im sporadischen Teil . Da sie jedoch nicht koklassen-stabil sind, werden ihre vollständigen Stammbäume unendlich.
- Drittens geben die drei Gruppen , und Anlass zu (unendlichen) Koklassen-Bäumen, nämlich , , , jeder davon mit metabelscher Hauptlinie, im periodischen Teil des Koklassen-Graphen . Wiederum ist keine dieser drei Gruppen koklassen-stabil.
Durch Hinzunahme zusätzlicher Informationen über Kerne und Ziele von Artin-Verlagerungen werden diese Bäume zu strukturierten Stammbäumen.
Definition. Allgemein versteht man unter einer Schur-Gruppe (von I. Schur selbst, der den Begriff prägte, noch geschlossene Gruppe genannt) eine pro-p Gruppe , deren Relationen-Rank mit ihrem Generatoren-Rank übereinstimmt. Eine σ-Gruppe ist eine pro-p Gruppe mit einem Automorphismus , der auf dem Kommutator-Quotienten die Inversion induziert. Schließlich versteht man unter einer Schur σ-Gruppe eine Schur-Gruppe , die zugleich eine σ-Gruppe ist und eine endliche Abelianisierung besitzt.
Als Warnung sei erwähnt, dass die Gruppe keine Wurzel eines Koklassen-Baums ist, denn ihr unmittelbarer Nachfolger , der die Wurzel eines Koklassen-Baums mit metabelschen Hauptlinien-Vertices ist, besitzt zwei Geschwister , beziehungsweise , die Anlass geben zu einem einzelnen, beziehungsweise drei, Koklassen-Bäumen mit nicht-metabelschen Hauptlinien-Vertices (alle mit zyklischem Zentrum der Ordnung ) und Zweigen von beträchtlicher Komplexität, die aber dennoch beschränkte Tiefe aufweisen.
| Parameter |
Abelisierung |
Klasse-2 Quotient |
Klasse-3 Quotient |
Klasse-4 Quotient |
|---|---|---|---|---|
Pro-3-Gruppen der Koklasse 2 mit nicht-trivialem Zentrum[Bearbeiten | Quelltext bearbeiten]
B. Eick, C. R. Leedham-Green, M. F. Newman und E. A. O’Brien[9] konstruierten im Jahr 2013 eine Familie unendlicher pro-3-Gruppen mit Koklasse und nicht-trivialem Zentrum der Ordnung . Die Mitglieder der Familie sind durch drei Parameter charakterisiert. Ihre endlichen Quotienten erzeugen alle Hauptlinien-Vertices mit bizyklischem Zentrum des Typs von sechs Koklassen-Bäumen im Koklassen-Graph . Die Assoziation der drei Parameter zu den Wurzeln dieser sechs Bäume ist in Tabelle 1 angegeben. Die Baumdiagramme, mit Ausnahme der Abelisierung , sind in den Abbildungen 4 und 5 dargestellt und die parametrisierte pro-3 Präsentation ist gegeben durch
Koklasse 3[Bearbeiten | Quelltext bearbeiten]
Auch hier tragen wieder -Gruppen mit mehreren verschiedenen Abelisierungen zur Konstitution des Koklassen-Graphen bei. Es gibt reguläre, beziehungsweise irreguläre, wesentliche Beiträge von Gruppen with Kommutator-Quotienten der Typen , , , , beziehungsweise , , , und einen isolierten Beitrag durch die zyklischen Gruppe der Ordnung .
Kommutator-Quotient vom Typ (p,p,p)[Bearbeiten | Quelltext bearbeiten]
Weil die elementar-abelsche -Gruppe vom Rang , das heißt, die Gruppe für , beziehungsweise die Gruppe für , nicht koklassen-stabil ist, gibt sie Anlass zu einer Multifurkation. Die reguläre Komponente ist im Abschnitt über Koklasse beschrieben worden. Die irreguläre Komponente wird zu einem Teilgraphen des Koklassen-Graphen , wenn man die verbindenden Kanten mit Schrittweite der irregulären unmittelbaren Nachfolger von entfernt.
Für ist dieser Teilgraph in Abbildung 6 enthalten. Er besitzt neun Top Level Vertices der Ordnung , welche man in terminale und erweiterbare Vertices einteilen kann.
- Die zwei Gruppen und sind terminal.
- Die fünf Gruppen und die zwei Gruppen sind unendlich erweiterbar.
Die aus den erweiterbaren Vertices entstehenden Bäume stehen auf folgende Weise in Zusammenhang mit unendlichen pro-2 Gruppen von M. F. Newman und E. A. O'Brien.[10]
- gibt Anlass zu zwei Bäumen,
- assoziiert mit der Familie , und
- assoziiert mit der Familie .
- ist assoziiert mit der Familie .
- ist assoziiert mit der Familie .
- ist assoziiert mit der Familie .
- gibt Anlass zu
- assoziiert mit der Familie . Schließlich ist
- assoziiert mit der Familie .
| SmallGroups Identifier von Q |
Hall Senior Klassifikation von Q |
Schur Multiplikator |
2-Rang von G' |
4-Rang von G' |
Maximum von |
|---|---|---|---|---|---|
| 32.040 | |||||
| 32.041 | |||||
| 32.037 | |||||
| 32.038 | |||||
| 32.035 | |||||
| 32.036 | |||||
| 32.033 | or |
Hall-Senior-Klassifikation von 2-Gruppen[Bearbeiten | Quelltext bearbeiten]
Sieben von diesen neun Top-Level-Vertices sind von E. Benjamin, F. Lemmermeyer und C. Snyder untersucht worden[23] im Hinblick auf ihr Vorkommen als Klasse-2-Quotienten größerer metabelscher 2-Gruppen des Typs und mit Koklasse , die exakt die Mitglieder der Stammbäume der sieben Vertices sind. Diese Autoren verwenden die Klassifikation der 2-Gruppen von M. Hall und J. K. Senior,[24] die in Tabelle 2 in Korrespondenz mit der SmallGroups Library[16] gesetzt wird. Die Komplexität der Stammbäume dieser sieben Vertices wächst mit den 2-Rängen und 4-Rängen, die in Tabelle 2 angegeben sind. Dort werden die maximalen Untergruppen vom Index in mit bezeichnet, für .
Geschichte[Bearbeiten | Quelltext bearbeiten]
Stammbäume mit Zentralquotienten als Vorgängern (V1) kommen implizit im Artikel[11] über Isoklinie von Gruppen von P. Hall aus dem Jahr 1940 vor. Bäume mit dem Quotienten nach der letzten nicht-trivialen unteren Zentrale als Vorgänger (V2) wurden erstmals von C. R. Leedham-Green am International Congress of Mathematicians, 1974 in Vancouver vorgestellt.[5] Die ersten umfangreichen Baumdiagramme sind manuell angefertigt worden von J. A. Ascione, G. Havas und C. R. Leedham-Green (1977),[25] von J. A. Ascione (1979),[18] und von B. Nebelung (1989).[26] In den ersteren beiden Fällen wurde, im Hinblick auf computertechnische Vorteile, die Vorgänger-Definition mittels der unteren Exponent-p Zentralreihe (V3) benützt. Im letzteren Fall, wo theoretische Aspekte im Brennpunkt lagen, wurden die Vorgänger in Bezug auf die gewöhnliche untere Zentralreihe (V2) definiert.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b c du Sautoy, M.: Counting -groups and nilpotent groups. In: Inst. Hautes Études Sci. Publ. Math. 92. Jahrgang, 2001, S. 63–112.
- ↑ a b c d Eick, B., Leedham-Green, C. R.: On the classification of prime-power groups by coclass. In: Bull. London Math. Soc. 40. Jahrgang, Nr. 2, 2008, S. 274–288, doi:10.1112/blms/bdn007.
- ↑ Bush, M. R., Mayer, D. C.: 3-Class field towers of exact length 3,. In: J. Number Theory. 147. Jahrgang, 2015, S. 766–777, doi:10.1016/j.jnt.2014.08.010.
- ↑ Gamble, G., Nickel, W., O'Brien, E. A.: ANU p-Quotient -- p-Quotient and p-Group Generation Algorithms. 2006, An Accepted GAP 4 Package, Available also in MAGMA.
- ↑ a b c Newman, M. F.: Groups—Canberra 1989 (= Lecture Notes in Mathematics. Band 1456). Springer, 1990, ISBN 978-3-540-53475-4, Groups of prime-power order, S. 49–62, doi:10.1007/bfb0100730.
- ↑ a b Leedham-Green, C. R., Newman, M. F.: Space groups and groups of prime power order I. In: Arch. Math. 35. Jahrgang, 1980, S. 193–203, doi:10.1007/bf01235338.
- ↑ a b du Sautoy, M., Segal, D.: New horizons in pro- groups (= Progress in Mathematics. Band 184). Birkhäuser, Basel 2000, Zeta functions of groups, S. 249–28.
- ↑ Leedham-Green, C. R., McKay, S.: The structure of groups of prime power order. In: London Mathematical Society Monographs. 27. Jahrgang. Oxford University Press, 2002.
- ↑ a b c d Eick, B., Leedham-Green, C. R., Newman, M. F., O'Brien, E. A.: On the classification of groups of prime-power order by coclass: the 3-groups of coclass 2. In: Int. J. Algebra Comput. 23. Jahrgang, Nr. 5, 2013, S. 1243–1288, doi:10.1142/s0218196713500252.
- ↑ a b Newman, M. F., O'Brien, E. A.: Classifying 2-groups by coclass. In: Trans. Amer. Math. Soc. 351. Jahrgang, 1999, S. 131–169, doi:10.1090/s0002-9947-99-02124-8.
- ↑ a b Hall, P.: The classification of prime-power groups. In: J. Reine Angew. Math. 182. Jahrgang, 1940, S. 130–141.
- ↑ Shalev, A.: The structure of finite -groups: effective proof of the coclass conjectures. In: Invent. Math. 115. Jahrgang, 1994, S. 315–345, doi:10.1007/bf01231763, bibcode:1994InMat.115..315S.
- ↑ Leedham-Green, C. R.: The structure of finite -groups. In: J. London Math. Soc. 50. Jahrgang, 1994, S. 49–67, doi:10.1112/jlms/50.1.49.
- ↑ Newman, M. F.: Determination of groups of prime-power order. pp. 73-84, in: Group Theory, Canberra, 1975, Lecture Notes in Math., Vol. 573, Springer, Berlin, 1977.
- ↑ O'Brien, E. A.: The -group generation algorithm. In: J. Symbolic Comput. 9. Jahrgang, Nr. 5–6, 1990, S. 677–698, doi:10.1016/s0747-7171(08)80082-x.
- ↑ a b Besche, H. U., Eick, B., O'Brien, E. A.: The SmallGroups Library – a library of groups of small order. An accepted and refereed GAP 4 package, available also in MAGMA, 2005.
- ↑ Besche, H. U., Eick, B., O'Brien, E. A.: A millennium project: constructing small groups. In: Int. J. Algebra Comput. 12. Jahrgang, Nr. 5, 2002, S. 623–644, doi:10.1142/s0218196702001115.
- ↑ a b Ascione, J. A.: On 3-groups of second maximal class. Ph. D. Thesis, Australian National University, Canberra, 1979.
- ↑ Dietrich, H., Eick, B., Feichtenschlager, D.: Contemporary Mathematics, Computational group theory and the theory of groups. Band 470. American Mathematical Society, Providence, RI, 2008, ISBN 978-0-8218-4365-9, Investigating p-groups by coclass with GAP, S. 45–61, doi:10.1090/conm/470/09185.
- ↑ Blackburn, N.: On a special class of p-groups. In: Acta Math. 100. Jahrgang, Nr. 1–2, 1958, S. 45–92, doi:10.1007/bf02559602.
- ↑ Taussky, O.: A remark on the class field tower. In: J. London Math. Soc. 12. Jahrgang, Nr. 2, 1937, S. 82–85, doi:10.1112/jlms/s1-12.1.82.
- ↑ a b Bagnera, G.: La composizione dei gruppi finiti il cui grado è la quinta potenza di un numero primo. In: Ann. Di Mat. (Ser. 3). 1. Jahrgang, 1898, S. 137–228, doi:10.1007/bf02419191 (zenodo.org).
- ↑ a b Benjamin, E., Lemmermeyer, F., Snyder, C.: Imaginary quadratic fields with <math>\mathrm{Cl}_2(k)\simeq (2,2,2)</math>. In: J. Number Theory. 103. Jahrgang, 2003, S. 38–70, doi:10.1016/S0022-314X(03)00084-2, arxiv:math/0207307.
- ↑ Hall, M., Senior, J. K.: The groups of order . Macmillan, New York, 1964.
- ↑ Ascione, J. A., Havas, G., Leedham-Green, C. R.: A computer aided classification of certain groups of prime power order. In: Bull. Austral. Math. Soc. 17. Jahrgang, Nr. 2, 1977, S. 257–274, doi:10.1017/s0004972700010467.
- ↑ Nebelung, B.: Klassifikation metabelscher 3-Gruppen mit Faktorkommutatorgruppe vom Typ (3,3) und Anwendung auf das Kapitulationsproblem. Inauguraldissertation, Universität zu Köln, 1989.




























































































































































































































































































































