Parallelepiped

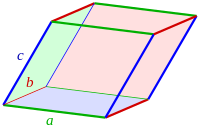
Ein Parallelepiped

Ein Parallelepiped oder Spat (früher auch Parallelflach) ist ein geometrischer Körper, der von 6 Parallelogrammen begrenzt wird, von denen je 2 gegenüber liegende kongruent (deckungsgleich) sind und in parallelen Ebenen liegen.

Ein Parallelepiped hat 12 Kanten, von denen je 4 parallel verlaufen und untereinander gleich lang sind, und 8 Ecken, in denen diese Kanten in maximal 3 verschiedenen Winkeln zueinander zusammenlaufen.

Quader, bei denen alle Winkel gleich 90° sind, und Rhomboeder, bei denen alle Kanten gleich lang und 3 Innenwinkel gleich sind, sind Spezialfälle des Parallelepipeds. Der Würfel vereinigt beide Spezialfälle in einer Figur. Das Parallelepiped ist ein spezielles Prisma mit einem Parallelogramm als Grundfläche.

Formeln

Volumen

Ein Parallelepiped wird von 3 Vektoren erzeugt.

Stellt man diese 3 an einer Ecke zusammentreffende Kanten als Vektoren ${\vec {a}},{\vec {b}},{\vec {c}}$ dar, so ergibt sich das Volumen des Parallelepipeds aus dem Betrag des Spatproduktes (gemischtes Skalarprodukt und Kreuzprodukt). Das Volumen $V$ ist das Produkt der Grundfläche $G$ (Parallelogramm) und der Höhe $h$ des Parallelepipeds. Mit $G=|{\vec {a}}|\cdot |{\vec {b}}|\cdot \sin(\gamma )=|{\vec {a}}\times {\vec {b}}|$, wobei $\gamma$ der Winkel zwischen ${\vec {a}}$ und ${\vec {b}}$ ist, und der Höhe $h=|{\vec {c}}|\cdot |\cos(\theta )|$, wobei $\theta$ der Winkel zwischen ${\vec {c}}$ und dem Normalenvektor auf der Grundfläche ist, ergibt sich

${\begin{aligned}V&=G\cdot h=(|{\vec {a}}|\cdot |{\vec {b}}|\cdot \sin(\gamma ))\cdot |{\vec {c}}|\cdot |\cos(\theta )|=|{\vec {a}}\times {\vec {b}}|\cdot |{\vec {c}}|\cdot |\cos(\theta )|\\&=|({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}|\end{aligned}}$

Das gemischte Produkt nennt man Spatprodukt. Es kann als Determinante geschrieben werden. Für ${\vec {a}}=(a_{1},a_{2},a_{3})^{T},\quad {\vec {b}}=(b_{1},b_{2},b_{3})^{T},\quad {\vec {c}}=(c_{1},c_{2},c_{3})^{T}$ ist das Volumen dann:

$V=\left|\det {\begin{pmatrix}a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\\a_{3}&b_{3}&c_{3}\end{pmatrix}}\;\right|$

Eine nur von den geometrischen Eigenschaften (Kantenlängen, Winkel zwischen benachbarten Kanten) abhängige Formel für das Volumen ist:

$V=a\cdot b\cdot c\cdot {\sqrt {1+2\cdot \cos(\alpha )\cdot \cos(\beta )\cdot \cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}$

Dabei sind $\alpha =\angle ({\vec {b}},{\vec {c}}),\quad \beta =\angle ({\vec {a}},{\vec {c}}),\quad \gamma =\angle ({\vec {a}},{\vec {b}})$ die Winkel zwischen den Kanten und $a,b,c$ die Kantenlängen.

Der Nachweis dieser Formel lässt sich mit den Eigenschaften einer Determinante und der geometrischen Deutung des Skalarprodukts führen. Es sei $M$ die 3x3-Matrix, deren Spaltenvektoren die Vektoren ${\vec {a}},{\vec {b}},{\vec {c}}$ sind. Dann gilt

${\begin{aligned}V^{2}&=(\det(M))^{2}=\det(M)\cdot \det(M)=\det(M^{T})\cdot \det(M)=\det(M^{T}\cdot M)\\&=\det {\begin{pmatrix}{\vec {a}}\cdot {\vec {a}}&{\vec {a}}\cdot {\vec {b}}&{\vec {a}}\cdot {\vec {c}}\\{\vec {b}}\cdot {\vec {a}}&{\vec {b}}\cdot {\vec {b}}&{\vec {b}}\cdot {\vec {c}}\\{\vec {c}}\cdot {\vec {a}}&{\vec {c}}\cdot {\vec {b}}&{\vec {c}}\cdot {\vec {c}}\end{pmatrix}}=a^{2}\cdot b^{2}\cdot c^{2}\cdot (1+2\cdot \cos(\alpha )\cdot \cos(\beta )\cdot \cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma ))\end{aligned}}$

Im letzten Schritt wurden die Gleichungen ${\vec {a}}\cdot {\vec {a}}=a^{2},\quad {\vec {b}}\cdot {\vec {b}}=b^{2},\quad {\vec {c}}\cdot {\vec {c}}=c^{2},\quad {\vec {a}}\cdot {\vec {b}}=a\cdot b\cdot \cos(\gamma ),\quad {\vec {a}}\cdot {\vec {c}}=a\cdot c\cdot \cos(\beta ),\quad {\vec {b}}\cdot {\vec {c}}=b\cdot c\cdot \cos(\alpha )$ benutzt.

Oberfläche

Körpernetz eines Parallelepipeds

Der Flächeninhalt der Oberfläche ergibt sich aus der Summe der Flächeninhalte der einzelnen Seitenflächen, den 6 Parallelogrammen:

${\begin{aligned}A&=2\cdot \left(|{\vec {a}}\times {\vec {b}}|+|{\vec {a}}\times {\vec {c}}|+|{\vec {b}}\times {\vec {c}}|\right)\\&=2\cdot a\cdot b\cdot \sin(\gamma )+2\cdot a\cdot c\cdot \sin(\beta )+2\cdot b\cdot c\cdot \sin(\alpha )\end{aligned}}$.

Flächenwinkel

In der Ecke, in der die Vektoren ${\vec {a}},{\vec {b}},{\vec {c}}$ zusammentreffen, liegen die Innenwinkel $\alpha =\angle ({\vec {b}},{\vec {c}}),\quad \beta =\angle ({\vec {a}},{\vec {c}}),\quad \gamma =\angle ({\vec {a}},{\vec {b}})$. Diese Ecke bildet zusammen mit den 3 benachbarten Ecken ein Tetraeder. Betrachtet man die Umkugel dieses Tetraeders, dann gilt nach dem Kosinussatz für Kugeldreiecke die Gleichung

$\cos(\alpha )=\cos(\beta )\cdot \cos(\gamma )+\sin(\beta )\cdot \sin(\gamma )\cdot \cos(\beta _{a})$

Dabei ist $\beta _{a}$ der Flächenwinkel zwischen den beiden Seitenflächen, die am Vektor ${\vec {a}}$ liegen.

Daraus folgt

$\beta _{a}=\arccos \left({\frac {\cos(\alpha )-\cos(\beta )\cdot \cos(\gamma )}{\sin(\beta )\cdot \sin(\gamma )}}\right)$

Die Flächenwinkel $\beta _{b}$ und $\beta _{c}$ ergeben sich entsprechend.

Raumwinkel

Der Raumwinkel in der Ecke eines Polyeders kann mit dem Satz von L'Huilier berechnet werden.

Für den Raumwinkel, der in der Ecke mit den Innenwinkeln $\alpha =\angle ({\vec {b}},{\vec {c}}),\quad \beta =\angle ({\vec {a}},{\vec {c}}),\quad \gamma =\angle ({\vec {a}},{\vec {b}})$ liegt, gilt

${\begin{aligned}\Omega _{1}&=4\cdot \arctan \left({\sqrt {\tan \left({\frac {\theta _{s}}{2}}\right)\cdot \tan \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\cdot \tan \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\cdot \tan \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}}\right)\\&=4\cdot \arctan \left({\sqrt {\tan \left({\frac {\alpha +\beta +\gamma }{4}}\right)\cdot \tan \left({\frac {-\alpha +\beta +\gamma }{4}}\right)\cdot \tan \left({\frac {\alpha -\beta +\gamma }{4}}\right)\cdot \tan \left({\frac {\alpha +\beta -\gamma }{4}}\right)}}\right)\end{aligned}}$

wobei $\theta _{s}={\frac {\alpha +\beta +\gamma }{2}}$, $\theta _{a}=\alpha$, $\theta _{b}=\beta$ und $\theta _{c}=\gamma$ ist.

Zwei diagonal gegenüber liegende Raumwinkel in Ecken des Parallelepipeds sind jeweils gleich, weil die 3 anliegenden Innenwinkel gleich sind. Die anderen drei Raumwinkel ergeben sich für

• $\theta _{a}=\alpha ,\quad \theta _{b}=180^{\circ }-\beta ,\quad \theta _{c}=180^{\circ }-\gamma$
• $\theta _{a}=180^{\circ }-\alpha ,\quad \theta _{b}=\beta ,\quad \theta _{c}=180^{\circ }-\gamma$
• $\theta _{a}=180^{\circ }-\alpha ,\quad \theta _{b}=180^{\circ }-\beta ,\quad \theta _{c}=\gamma$

Tabelle: Zusammenfassung

Größen eines Parallelepipeds mit den Kantenlängen a, b, c und den Innenwinkeln $\alpha$, $\beta$, $\gamma$
Parallelelepiped
Volumen	$V=a\cdot b\cdot c\cdot {\sqrt {1+2\cdot \cos(\alpha )\cdot \cos(\beta )\cdot \cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}$
Oberflächeninhalt	$A=2\cdot a\cdot b\cdot \sin(\gamma )+2\cdot a\cdot c\cdot \sin(\beta )+2\cdot b\cdot c\cdot \sin(\alpha )$
Höhe	$h={\frac {a}{\sin(\alpha )}}\cdot {\sqrt {1+2\cdot \cos(\alpha )\cdot \cos(\beta )\cdot \cos(\gamma )-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )}}$
Raumdiagonale $|{\vec {a}}+{\vec {b}}+{\vec {c}}|$	$d={\sqrt {a^{2}+b^{2}+c^{2}+2\cdot a\cdot b\cdot \sin(\gamma )+2\cdot a\cdot c\cdot \sin(\beta )+2\cdot b\cdot c\cdot \sin(\alpha )}}$
Winkel zwischen benachbarten Flächen	$\beta _{a}=\arccos \left({\frac {\cos(\alpha )-\cos(\beta )\cdot \cos(\gamma )}{\sin(\beta )\cdot \sin(\gamma )}}\right)$
Raumwinkel in den Ecken	$\Omega _{1}=4\cdot \arctan \left({\sqrt {\tan \left({\tfrac {\alpha +\beta +\gamma }{4}}\right)\cdot \tan \left({\tfrac {-\alpha +\beta +\gamma }{4}}\right)\cdot \tan \left({\tfrac {\alpha -\beta +\gamma }{4}}\right)\cdot \tan \left({\tfrac {\alpha +\beta -\gamma }{4}}\right)}}\right)$

Raumfüllung mit Parallelepipeden

Der dreidimensionale euklidische Raum kann lückenlos mit kongruenten Parallelepipeden ausgefüllt werden kann. Solche dreidimensionalen Parkettierungen werden Raumfüllung genannt.

Diese Raumfüllung aus Parallelepipeden bildet ein Gitter. Dieses Gitter enthält parallele Ebenen. Die im Gitter benachbarten Raumwinkel $\Omega _{1}$ und $\Omega _{2}$ entsprechen zusammen dem Flächenwinkel $\beta _{a}$. Der volle Flächenwinkel beträgt $2\cdot \pi$ und der volle Raumwinkel beträgt $4\cdot \pi \ \mathrm {sr}$. Daher gilt $\beta _{a}={\frac {\Omega _{1}+\Omega _{2}}{2}}$. Entsprechend gilt $\beta _{b}={\frac {\Omega _{1}+\Omega _{3}}{2}}$ und $\beta _{c}={\frac {\Omega _{1}+\Omega _{4}}{2}}$.

In den Gitterpunkten treffen 8 Raumwinkel zusammen und bilden einen vollen Raumwinkel, wobei 2 diagonal gegenüber liegende Raumwinkel jeweils gleich sind. Es gilt also $2\cdot \Omega _{1}+2\cdot \Omega _{2}+2\cdot \Omega _{3}+2\cdot \Omega _{4}=4\cdot \pi \ \mathrm {sr}$.

Verallgemeinerung

Das Parallelotop beziehungsweise n-Parallelotop ist eine Verallgemeinerung des Parallelepipeds im n-dimensionalen Raum. Das zweidimensionale Parallelotop ist das Parallelogramm.

Ein n-Parallelotop ist das Bild des Einheitswürfels unter einer affinen Abbildung. Der Einheitswürfel $I^{n}$ ist eine Menge von Punkten, deren Koordinaten einen Wert zwischen 0 und 1 annehmen, das heißt

$I^{n}:=\left\{(x_{1},\dots ,x_{n})\mid 0\leq x_{i}\leq 1\right\}$

Das Parallelotop ist ein konvexes Polytop mit $2^{n}$ Ecken. Für $m<n$ sind seine m-dimensionalen Seiten selbst m-dimensionale Parallelotope.

Literatur

• Konrad Königsberger: Analysis. Band 2. Springer, Berlin 2004, ISBN 3-540-20389-3.

Siehe auch

• Quader
• Rhomboeder

Weblinks

Commons: Parallelepipeds – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Parallelepiped – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Definition des Parallelepipeds aus den Mathematik-Vorlesungen der Universität Stuttgart, abgerufen am 6. Dezember 2020
• Formeln zum Parallelepiped aus dem Duden-Schülerlexikon, abgerufen am 6. Dezember 2020
• Formeln, Beispiele und Übungen zum Parallelepiped aus mein-lernen.at, abgerufen am 6. Dezember 2020
• Parallelepiped-Rechner aus rechneronline.de, abgerufen am 6. Dezember 2020