Binomische Formeln

also zum Beispiel:
Die binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zum Umformen von Produkten aus Binomen. Mit Binomen (deutsch: „zwei Namen“; eine Bezeichnung, die auf Euklid zurückgeht) sind mathematische Ausdrücke mit zwei Gliedern gemeint, die durch Addition oder Subtraktion verbunden sind, wie zum Beispiel
- oder auch (mit zwei noch nicht näher bestimmten Zahlen und ).
In einigen Anwendungen ist das Rechnen mit quadrierten Binomen vonnöten: Zerteilt man in der Geometrie zum Beispiel die Seite eines Quadrates in die Längen und so hat es den Flächeninhalt (siehe Bild). Es bedeutet die Schreibweise (gesprochen: „ Quadrat“), dass die Zahl mit sich selbst multipliziert wird, also Zum Beispiel gilt .
Innerhalb der Schulmathematik kommt den binomischen Formeln ein hoher Stellenwert zu, und sie sind fester Bestandteil des Lehrplans im Fach Mathematik. Gerade im Umgang mit der Quadratur von Summen passieren in der mathematischen Ausbildung häufig Fehler: So ist das „Quadrat einer Summe“, also zum Beispiel im Allgemeinen[Anm. 1] nicht die „Summe der Quadrate“, hier Da Klammern stets zuerst aufgelöst werden müssen, gilt
- aber
Die binomischen Formeln halten nun Rechenregeln fest, mit deren Hilfe zum Beispiel der Ausdruck korrekt „in Abhängigkeit von und “, also der zwei Glieder des Binoms, berechnet werden kann, insbesondere unter Beachtung aller Regeln für Klammerausdrücke. Diese Regeln entfalten ganz besonders dann ihren Sinn, wenn nicht alle Teile des Binoms bestimmt sind, zum Beispiel aber trotzdem eine Berechnung bzw. Umformung gemacht werden soll. Vorteile hat dies zum Beispiel beim Umgang mit quadratischen Gleichungen. Weitere Anwendungen betreffen quadratische Ergänzung, einen Beweis des Satzes des Pythagoras, aber auch Bereiche wie Analysis und Wahrscheinlichkeitstheorie.
Die binomischen Formeln werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern und Rechenfehler verhindern sollen, zum anderen erlauben sie die Faktorisierung von Termen, also die Umformung von bestimmten Summen und Differenzen in Produkte, was bei der Vereinfachung von Bruchtermen oder Wurzeltermen sehr oft die einzige Lösungsstrategie darstellt. Im Grunde sind sie nur Anwendungen des Distributivgesetzes für algebraische Summen (jedes Glied der einen wird mit jedem der anderen Summe multipliziert)
mit und den entsprechenden Vorzeichenvarianten. Erstmals bewiesen wurden die binomischen Formeln von Euklid, der geometrische Methoden verwendete. Sie waren aber den Babyloniern bereits 1900 v. Chr. bekannt.
Eine Verallgemeinerung der binomischen Formeln auf beliebige natürliche Exponenten, wie usw., stellt der binomische Lehrsatz dar. Die binomischen Formeln gelten in allen kommutativen Ringen (allgemeine Mengen, innerhalb derer mit Addition, Subtraktion und Multiplikation gerechnet werden kann, wie etwa die ganzen Zahlen).
Formeln[Bearbeiten | Quelltext bearbeiten]
Aussage der Formeln[Bearbeiten | Quelltext bearbeiten]
Als binomische Formeln werden (im Rahmen der Schulmathematik)[1][2] üblicherweise die folgenden drei Umformungen mit dem Exponenten 2 bezeichnet:[3]
| erste binomische Formel, | |
| zweite binomische Formel, | |
| dritte binomische Formel. |
Es werden die Terme und als quadratische Glieder und als gemischtes Glied bezeichnet.[4] Zu beachten ist die übliche Kurzschreibweise für das Produkt Das Wort „binomisch“ rührt vom Begriff Binom her und bedeutet, dass es sich um Berechnungen mit Termen mit zwei Gliedern (= Zahlen oder Unbekannte) handelt, wobei diese Glieder miteinander addiert oder subtrahiert werden.[5]
Die binomischen Formeln halten bestimmte Rechengesetze in größtmöglicher Allgemeinheit fest. Daher werden Zahlen hier (willkürlich) durch die Buchstaben und ersetzt. Die Absicht dahinter ist, eine möglichst große Bandbreite an Anwendungen zu gewährleisten, denn mit unterschiedlichen Anwendungen können immer auch unterschiedliche Zahlen verbunden sein. Ein besseres Gefühl und Verständnis kann beim Üben an konkreten Zahlen erreicht werden. Eine Anwendung der zweiten binomischen Formel ist etwa
In der Tat gilt da Klammerinhalte zuerst berechnet werden müssen.
Herleitung[Bearbeiten | Quelltext bearbeiten]

Die Gültigkeit der Formeln ist durch Ausmultiplizieren einzusehen:
Sie sind damit nur Anwendungen des Distributivgesetzes für algebraische Summen. Jedes Glied der einen wird dabei mit jedem der anderen Summe multipliziert:
mit und den entsprechenden Vorzeichenvarianten.
Nachbemerkungen[Bearbeiten | Quelltext bearbeiten]
Obwohl die zweite binomische Formel als eigenständige Formel geführt wird, ergibt sie sich unmittelbar aus der ersten binomischen Formel „angewendet auf und “. Es gilt mit der ersten binomischen Formel
Wegen des Kommutativgesetzes ist das Vertauschen von Faktoren in Produkten erlaubt. Daher spielt es für die dritte binomische Formel keine Rolle, wann die Terme auftauchen. Es gilt
Bei den binomischen Formeln handelt es sich nicht um Gleichungen im herkömmlichen Sinne, sondern um Identitäten; die Gleichheit beider Ausdrücke auf der linken und rechten Seite des Gleichheitszeichens ist also für jede Auswahl von Zahlen oder Unbekannten gegeben. Hingegen müssen spezielle Gleichungen oft aufgelöst werden, und nur eine eingeschränkte Menge an Zahlen werden diese lösen. Zur Betonung der universellen Gültigkeit kann daher auch das Symbol genutzt werden, zum Beispiel
Die Wahl der Buchstaben und ist entsprechend willkürlich; es handelt sich nur um Platzhalter für Zahlen, deren genaue Benennung keinen Einfluss auf die Formeln hat. Die einzige Ausnahme hiervon ist, dass im Allgemeinen verschiedene Größen ungleich benannt werden sollten. So kann die erste binomische Formel auch durch ausgedrückt werden, aber theoretisch auch durch Ungünstig hingegen ist die Bezeichnung da dies nur ein Spezialfall der allgemeinen Formel ist.
Im Gegensatz zu Adjektiven wie abelsch leitet sich binomisch nicht vom Namen eines Mathematikers ab. Im Sinne des wissenschaftlichen Witzes wird die Bezeichnung binomisch scherzhaft auf einen fiktiven Mathematiker namens Alessandro (oder Francesco) Binomi zurückgeführt, der wahlweise auch in einigen Schul- und Lehrbüchern als deren Urheber auftaucht.[6][7]
Rechenbeispiele[Bearbeiten | Quelltext bearbeiten]
Unmittelbare Bedeutung für den Alltag können binomische Formeln als Stütze beim Kopfrechnen haben.[8][9] Das Quadrat einer beliebigen Zahl zwischen 10 und 100 lässt sich oft einfach mit der binomischen Formel bestimmen, indem man die Berechnung auf Quadrate von einfacheren Zahlen (Vielfache von 10 oder einstellige Zahlen) zurückführt.
Beispielsweise ist mit der ersten binomischen Formel
oder alternativ mit der zweiten binomischen Formel
Bei Kenntnis einiger Quadratzahlen (etwa bis zum Wert ) lassen sich auch viele Multiplikationen auf die dritte binomische Formel zurückführen. Beispielsweise ist
oder auch
Der Trick klappt besonders gut, wenn die zu multiplizierenden Zahlen nahe beieinander liegen:
Ist der Abstand der zu multiplizierenden Zahlen eine ungerade Zahl, kann ein Summand abgespalten werden, zum Beispiel
Dabei werden also entscheidende Rechenschritte durch memorierte Zahlenzusammenhänge ersetzt. Die Flexibilität der Methode ermöglicht es, schon bei einer verhältnismäßig geringen Anzahl auswendig gelernter Quadratzahlen eine beachtliche Anzahl an Produkten ausrechnen zu können.
Weitere Beispiele sind:
Beispiel 1: Im Kontext der Schul- und Berufsmathematik tauchen die binomischen Formeln auch verstärkt bei Termumformungen auf. Dabei ist es nicht unüblich, dass sie zusammen mit anderen Rechenregeln kombiniert werden müssen. Ein Beispiel ist die Expandierung des Ausdrucks
Neben der zweiten binomischen Formel müssen hier auch die Potenzgesetze angewendet werden:
Beispiel 2: Bei Termen der Form also mit „falscher Vorzeichenreihenfolge“, kann die zweite binomische Formel verwendet werden. Jedoch kann es hilfreich sein, zuerst die Reihenfolge der Summanden in der Klammer zu vertauschen, damit die Struktur der Formel besser sichtbar wird. Es gilt in diesem Fall:
Beispiel 3: Im Falle eines „doppelten Minus“ ist eine Rückführung auf die erste binomische Formel schnell möglich, indem man das Minus in beiden Fällen weglässt. Dies entspricht einem Ausklammern und Quadrieren des Vorzeichens, was es verschwinden lässt. Es gilt also zum Beispiel
Selbstverständlich klappt aber auch die „direkte Berechnung“ mittels
bei der das Minus als fester Teil der Glieder gesehen wird.
Geometrische Veranschaulichung[Bearbeiten | Quelltext bearbeiten]

Es ist üblich und gut möglich, die binomischen Formeln – etwa im Rahmen des Schulunterrichts – geometrisch zu veranschaulichen. Dafür eignen sich die unten gezeigten Situationen aus der elementaren Geometrie.[10][11] Als Vorwissen muss bekannt sein, dass sich der Flächeninhalt eines Rechtecks mit Seitenlängen und über berechnet.
Erste binomische Formel:

Das nebenstehende mehrfarbige Quadrat hat die Seitenlänge Wie sofort ersichtlich ist, passen die zwei Quadrate und hinein, und es bleiben zwei Rechtecke mit jeweils dem Flächeninhalt übrig. Die Fläche des ganzen Quadrats hat also den Wert
Zweite binomische Formel:

Im zweiten Bild ist das blau umrahmte Quadrat (großes Quadrat, also, trotz gleicher Bezeichnung wie in der ersten binomischen Formel, ein anderes Quadrat!). Soll daraus ein Quadrat der Seitenlänge erzeugt werden, wird zuerst die rot umrahmte Fläche (das Rechteck) abgezogen (auch wieder, trotz gleicher Bezeichnung wie in der ersten binomischen Formel, ein anderes Rechteck). Danach wird die ebenso große, liegende Fläche abgezogen. Nun hat man aber das kleine Quadrat doppelt abgezogen, man muss es (zur Korrektur) noch einmal addieren.
Die hier gezeigte Formel lautet also [12]
Dritte binomische Formel:
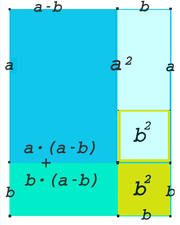
Im dritten Bild ist das hell- und dunkelblaue Quadrat. Wird das kleine Quadrat (gelber Rahmen) davon abgezogen und das verbleibende hellblaue Rechteck gedreht unten angehängt (türkis dargestellt), so entsteht (aus der dunkelblauen und türkisfarbenen Fläche) ein Rechteck der Breite und der Höhe
Also ergibt sich die Formel [14]
Eine weitere Veranschaulichung der dritten binomischen Formel erhält man durch folgende Zerlegung:
-
Veranschaulichung der dritten binomischen Formel über einen Perspektivwechsel: Die blaue Fläche wird geflippt, um zum zweiten Bild zu gelangen.[15]
Zu beachten ist, dass diese Veranschaulichungen zunächst im Allgemeinen nur für Werte funktionieren. Die Gültigkeit der Formeln bleibt aber auch etwa im Falle negativer Zahlen bestehen, was sich aus dem Distributivgesetz und damit letztlich den axiomatischen Rechenregeln in den reellen Zahlen, ergibt.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Die Entdeckungs- und Forschungsgeschichte der binomischen Formeln lässt sich bis auf 1900 v. Chr. in das babylonische Reich zurückdatieren. Einen ersten Beweis, basierend auf geometrischen Argumenten, konnte jedoch erst Euklid von Alexandria in seinen Elementen erbringen. Wegen der engen Verknüpfung zur Geometrie von Flächen war es Euklid naturgemäß nicht möglich, dies auf höhere Exponenten zu verallgemeinern. Eine kubische Variante der ersten binomischen Formel wurde einige Jahrhunderte später in Indien unter anderem durch Brahmagupta gegeben. In der moderneren Forschung sind die binomischen Formeln jedoch unzertrennlich mit ihren Verallgemeinerungen auf höhere Exponenten – also dem binomischen Lehrsatz – verbunden, weshalb diese Abgrenzung heutzutage nur noch im Rahmen der Schulmathematik üblich ist.
Bei den Babyloniern[Bearbeiten | Quelltext bearbeiten]
Nach heutigem Forschungsstand waren die erste und dritte binomische Formel wesentliche Inhalte der Algebra in Mesopotamien im Zeitraum 1900 bis 1600 v. Chr.[16]
Im Zusammenhang mit Berechnungen von Flächen stießen die Babylonier auf quadratische Gleichungen. Um diese zu lösen, entwickelten sie bereits Verfahren, die den heutigen ähneln. Wie Texte aus der Zeit der Hammurapi-Dynastie um das Jahr 1700 v. Chr. belegen, verfügten sie über Algorithmen (also „mathematische Vorgehensweisen“), mit denen sie die Lösung gemäß der heute üblichen Formel berechnen konnten, wobei jedoch die Frage offen bleibt, wie sie diese genau fanden. Da sie jedoch über die dritte binomische Formel verfügten, wird angenommen, dass sie ähnlich vorgingen wie später Diophantos von Alexandria.[17]

Die Babylonier verwendeten die erste binomische Formel auch für die Annäherung von Quadratwurzeln (siehe auch Heron-Verfahren). Ist im Vergleich zu klein, so ist zu erwarten, dass
mit einem kleinen gilt. Quadriert man dies, ergibt sich mit der ersten binomischen Formel
Vernachlässigt man ergibt sich daraus die Näherung also
Dies ist besonders dann praktisch, wenn eine Quadratzahl ist. Höchstwahrscheinlich auf diesen Gedanken aufbauend konnten die Babylonier die Quadratwurzel aus 2 durch annähern, wobei die Kommas die Ziffern im Sechzigersystem trennen, mit dem die Babylonier rechneten, was in Dezimalschreibweise ungefähr entspricht. Dies belegen Steintafeln aus dem Jahr 1900 v. Chr.[18] Der exakte Wert von beginnt mit
Im antiken Griechenland[Bearbeiten | Quelltext bearbeiten]
Beweis durch Euklid[Bearbeiten | Quelltext bearbeiten]
Bewiesen wurde die binomische Formel von Euklid von Alexandria (circa 3. Jahrhundert v. Chr.) in seinen Elementen. Euklids Beweismethode ist geometrisch, womit er die Formel ebenfalls in Buch II, Proposition 4 (Buch II: „Geometrische Algebra“) geometrisch interpretiert.[19] Die Bezeichnung „Binom“ geht ebenfalls auf Euklid zurück.[20]
| Details zu Euklids Beweis der ersten binomischen Formel (mit Originaltext und Übersetzung) | |
|
Euklids Ausführung kann wie folgt ins Deutsche übersetzt werden: | |
| Originaltext (griechisch) | Übersetzung |
|---|---|
|
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ. Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ. λέγω, ὅτι τὸ ἀπὸ τῆς ΑΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ. Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ, καὶ ἐπεζεύχθω ἡ ΒΔ, καὶ διὰ μὲν τοῦ Γ ὁποτέρᾳ τῶν ΑΔ, ΕΒ παράλληλος ἤχθω ἡ ΓΖ, διὰ δὲ τοῦ Η ὁποτέρᾳ τῶν ΑΒ, ΔΕ παράλληλος ἤχθω ἡ ΘΚ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΓΖ τῇ ΑΔ, καὶ εἰς αὐτὰς ἐμπέπτωκεν ἡ ΒΔ, ἡ ἐκτὸς γωνία ἡ ὑπὸ ΓΗΒ ἴση ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΑΔΒ. ἀλλ’ ̓ἡ ὑπὸ ΑΔΒ τῇ ὑπὸ ΑΒΔ ἐστιν ἴση, ἐπεὶ καὶ πλευρὰ ἡ ΒΑ τῇ ΑΔ ἐστιν ἴση· καὶ ἡ ὑπὸ ΓΗΒ ἄρα γωνιά τῇ ὑπὸ ΗΒΓ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΒΓ πλευρᾷ τῇ ΓΗ ἐστιν ἴση· ἀλλ’ ̓ἡμὲν ΓΒ τῇ ΗΚ ἐστινἴση. ἡδὲ ΓΗ τῇ ΚΒ· καὶ ἡ ΗΚ ἄρα τῇ ΚΒ ἐστιν ἴση· ἰσόπλευρον ἄρα ἐστὶ τὸ ΓΗΚΒ. λέγω δή, ὅτι καὶ ὀρθογώνιον. ἐπεὶ γὰρ παράλληλός ἐστιν ἡ ΓΗ τῇ ΒΚ [καὶ εἰς αὐτὰς ἐμπέπτωκεν εὐθεῖα ἡ ΓΒ], αἱ ἄρα ὑπὸ ΚΒΓ, ΗΓΒ γωνίαι δύο ὀρθαῖς εἰσιν ἴσαι. ὀρθὴ δὲ ἡ ὑπὸ ΚΒΓ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΒΓΗ· ὥστε καὶ αἱ ἀπεναντίον αἱ ὑπὸ ΓΗΚ, ΗΚΒ ὀρθαί εἰσιν. ὀρθογώνιον ἄρα ἐστὶ τὸ ΓΗΚΒ· ἐδείχθη δὲ καὶ ἰσόπλευρον· τετράγωνον ἄρα ἐστίν· καί ἐστιν ἀπὸ τῆς ΓΒ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΘΖ τετράγωνόν ἐστιν· καί ἐστιν ἀπὸ τῆς ΘΗ, τουτέστιν [ἀπὸ] τῆς ΑΓ· τὰ ἄρα ΘΖ, ΚΓ τετράγωνα ἀπὸ τῶν ΑΓ, ΓΒ εἰσιν. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΑΗ τῷ ΗΕ, καί ἐστι τὸ ΑΗ τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἴση γὰρ ἡ ΗΓ τῇ ΓΒ· καὶ τὸ ΗΕ ἄρα ἴσον ἐστὶ τῷ ὑπὸ ΑΓ, ΓΒ· τὰ ἄρα ΑΗ, ΗΕ ἴσα ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. ἔστι δὲ καὶ τὰ ΘΖ, ΓΚ τετράγωνα ἀπὸ τῶν ΑΓ, ΓΒ· τὰ ἄρα τέσσαρα τὰ ΘΖ, ΓΚ, ΑΗ, ΗΕ ἴσα ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ. ἀλλὰ τὰ ΘΖ, ΓΚ, ΑΗ, ΗΕ ὅλον ἐστὶ τὸ ΑΔΕΒ, ὅ ἐστιν ἀπὸ τῆς ΑΒ τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΑΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ. Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ· ὅπερ ἔδει δεῖξαι·[21] |
Wird eine Strecke in zwei geteilt, dann ist das Quadrat über der ganzen Strecke gleich den Quadraten über den Teilen und dem doppelten Rechteck, das die Teile ergeben, zusammen. Wenn die Strecke AB in C geteilt ist, dann, sage ich, ist das Quadrat über AB gleich den Quadraten über AC und CB und dem doppelten Rechteck aus AC und CB zusammen. Denn wird über AB das Quadrat ADEB errichtet, BD gezogen, durch C die zu AD und EB parallele CF und durch G die zu AB und DE parallele HK gezogen, dann ist an den Parallelen CF und AD, die von BD geschnitten werden, der äußere Winkel CGB gleich dem innen gegenüber liegenden Winkel ADB. Es ist der Winkel ADB gleich ABD, denn BA ist gleich AD und der Winkel CGB gleich GBC. Da BC gleich CG ist, sind auch CB und GK gleich, sowie CG und KB. Also ist das Viereck CGKB gleichseitig. Ich sage, es ist auch rechtwinklig. Da CG parallel zu BK ist, sind die Winkel KBC und GCB zusammen gleich zwei rechten. Also ist KBC ein rechter Winkel, ebenso wie BCG. Die gegenüber liegenden Winkel CGK und GKB sind rechte Winkel, also ist CGKB eine Rechteck und weil auch gleichseitig, ein Quadrat, das über CB errichtet ist. Aus den gleichen Gründen ist auch HDFG ein Quadrat, das über HG, das gleich AC ist, errichtet ist. Die Quadrate HDFG und CGKB sind deshalb gleich den Quadraten über AC und CB. Das Rechteck AHGC ist gleich GFEK. AHGC ergibt sich aus AC mit CB, also ergibt sich auch HFEK aus AC mit CB. Somit sind AHGC und GFEK zusammen gleich dem Doppelten des Rechtecks aus AC mit CB. Es sind damit HDFG, CGKB, AHGC und GFEK zusammen gleich den Quadraten über AC und CB und dem Doppelten des Rechtecks aus AC mit CB zusammen. Es sind aber HDFG, CGKB, AHGC und GFEK zusammen ADEB und dies ist das Quadrat über AB. Das Quadrat über AB ist deshalb gleich den Quadraten über AC und CB und dem Doppelten des Rechtecks aus AC und CB zusammen. Deshalb ist das Quadrat über einer zweigeteilten Strecke gleich den Quadraten über den Teilen und dem doppelten Rechteck, das die Teile ergeben, was zu zeigen war.[22] |
| |
Euklid beweist in Buch II, Proposition 5 auch die dritte binomische Formel, jedoch in der abgewandelten Form [23] Erneut basiert der Beweis auf geometrischen Überlegungen.
| Details zu Euklids Beweis der dritten binomischen Formel (mit Originaltext und Übersetzung) | |
|
Euklids Ausführung kann wie folgt ins Deutsche übersetzt werden: | |
| Originaltext (griechisch) | Übersetzung |
|---|---|
|
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὸ ὑπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ἡμισείας τετραγώνῳ. Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω εἰς μὲν ἴσα κατὰ τὸ Γ, εἰς δὲ ἄνισα κατὰ τὸ Δ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ τετραγώνῳ. Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΓΒ τετράγωνον τὸ ΓΕΖΒ, καὶ ἐπεζεύχθω ἡ ΒΕ, καὶ διὰ μὲν τοῦ Δ ὁποτέρᾳ τῶν ΓΕ, ΒΖ παράλληλος ἤχθω ἡ ΔΗ, διὰ δὲ τοῦ Θ ὁποτέρᾳ τῶν ΑΒ, ΕΖ παράλληλος πάλιν ἤχθω ἡ ΚΜ, καὶ πάλιν διὰ τοῦ Α ὁποτέρᾳ τῶν ΓΛ, ΒΜ παράλληλος ἤχθω ἡ ΑΚ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΓΘ παραπλήρωμα τῷ ΘΖ παραπληρώματι, κοινὸν προσκείσθω τὸ ΔΜ· ὅλον ἄρα τὸ ΓΜ ὅλῳ τῷ ΔΖ ἴσον ἐστίν. ἀλλὰ τὸ ΓΜ τῷ ΑΛ ἴσον ἐστίν, ἐπεὶ καὶ ἡ ΑΓ τῇ ΓΒ ἐστιν ἴση· καὶ τὸ ΑΛ ἄρα τῷ ΔΖ ἴσον ἐστίν. κοινὸν προσκείσθω τὸ ΓΘ· ὅλον ἄρα τὸ ΑΘ τῷ ΜΝΞ† γνώμονι ἴσον ἐστίν. ἀλλὰ τὸ ΑΘ τὸ ὑπὸ τῶν ΑΔ, ΔΒ ἐστιν· ἴση γὰρ ἡ ΔΘ τῇ ΔΒ· καὶ ὁ ΜΝΞ ἄρα γνώμων ἴσος ἐστὶ τῷ ὑπὸ ΑΔ, ΔΒ. κοινὸν προσκείσθω τὸ ΛΗ, ὅ ἐστιν ἴσον τῷ ἀπὸ τῆς ΓΔ· ὁ ἄρα ΜΝΞ γνώμων καὶ τὸ ΛΗ ἴσα ἐστὶ τῷ ὑπὸ τῶν ΑΔ, ΔΒ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΓΔ τετραγώνῳ. ἀλλὰ ὁ ΜΝΞ γνώμων καὶ τὸ ΛΗ ὅλον ἐστὶ τὸ ΓΕΖΒ τετράγωνον, ὅ ἐστιν ἀπὸ τῆς ΓΒ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ τετραγώνῳ. Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὸ ὑπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ἡμισείας τετραγώνῳ. ὅπερ ἔδει δεῖξαι.[21] |
Ist eine Strecke an einem Punkt in zwei gleiche Teile geteilt und in einem anderen Punkt in zwei ungleiche Teile, dann sind das Rechteck, das die ungleichen Teile ergeben, und das Quadrat über der Strecke zwischen den teilenden Punkten zusammen gleich dem Quadrat über der halben Strecke. Wenn die Strecke AB im Punkt C in zwei gleiche Teile geteilt wird und im Punkt D in zwei ungleiche Teile, dann, sage ich, ist das Rechteck, das AD mit DB ergibt, zusammen mit dem Quadrat über CD gleich dem Quadrat über CB. Es ist das Quadrat CEFB über CB zu errichten, die Diagonale BE zu ziehen, sodann durch D die zu CE und BF parallele DG, durch H die zu AB und EF parallele KM, sowie durch A die zu CL und BM parallele AK zu legen. Das Rechteck CDHL ist gleich dem Rechteck HMFG; beiden das gleiche Quadrat über DB hinzugefügt, ist dann das Rechteck CBML gleich dem Rechteck DBFG. Das Rechteck CBML ist gleich dem Rechteck ACLK, denn AC ist gleich CB; beiden das gleiche Rechteck CDHL hinzugefügt, ist das Rechteck aus AD mit DH gleich dem Gnomon CBFH und, da DH gleich DB ist, auch gleich dem Rechteck aus AD mit DB. Diesen beiden das gleiche Quadrat über LH, das dem Quadrat über CD gleich ist, hinzugefügt, ist das Rechteck aus AD mit DB zusammen mit dem Quadrat über CD gleich CBFE, da das Gnomon CBFH das Quadrat über LH zum Quadrat CBFE ergänzt. CBFE ist aber das Quadrat über CB. Also ist das Rechteck aus AD mit DB zusammen mit dem Quadrat über CD gleich dem Quadrat über CB. Deshalb ist bei einer Strecke, die in einem Punkt in zwei gleiche und in einem anderen Punkt in zwei ungleiche Teile geteilt ist, das Rechteck, das die ungerade Teile ergeben, zusammen mit dem Quadrat über der Strecke der teilenden Punkte gleich dem Quadrat über der halben Strecke, was zu zeigen war.[24] |
| |

In dieser Hinsicht ist die bereits im antiken Griechenland entdeckte Beziehung zwischen Algebra und Geometrie bemerkenswert. Laut Sonja Brentjes und Peter Schreiber sei „die einzig sinnvolle Antwort“ auf die Frage, wozu die Griechen überhaupt Algebra brauchten, die analytische Behandelbarkeit komplizierter geometrischer Sachverhalte. Sobald man von Geraden und Kreisen zu Kegelschnitten oder anderen „höheren Kurven“ übergehe, könnten diese in der Regel „nur durch Gleichungen zwischen bestimmten beteiligten Strecken“ definiert werden.[25] Zum Beispiel wird der Kreis mit Radius und dem Ursprung als Mittelpunkt über die algebraische Gleichung beschrieben. Euklid scheine dies schon erkannt zu haben, denn sein Beweis des Satzes des Pythagoras am Ende von Buch I seiner Elemente könne als eine „Motivation für das der geometrischen Algebra gewidmete Buch II“ gesehen werden, wo nun „ganz systematisch die algebraischen Grundeigenschaften der geometrisch interpretierten Addition und Multiplikation von Größen“ abgehandelt werden.[26]
Der Mathematikhistoriker Sabetai Unguru vertritt in seinem Artikel On the Need to Rewrite the History of Greek Mathematics die These, dass die Darstellung antiker Mathematik durch moderne Algebra problematisch sei. Unguru ist der Auffassung, dass es prinzipiell unangemessen sei, antike Erkenntnisse mit modernen Formeln darzustellen. Er bezeichnete die „geometrische Algebra“ als ein „Fantasiegespinst, ein monströses Zwittergeschöpf, das sich Mathematiker ausgedacht haben, denen jegliches Gefühl für Historie fehlt“.[27][28] Der Formel- und Begriffsapparat der modernen Mathematik beinhalte Konzepte und Abstraktionen, die „das Authentische am historischen Vorgehen möglicherweise verschleiern“. Als Beispiel könne die binomische Formel angeführt werden.[29] In der modernen Mathematik gilt sie für alle abstrakten Elemente eines kommutativen Rings (einer Menge, in der Elemente addiert und multipliziert werden können); eine solche Begriffsbildung sei einem Euklid jedoch völlig fremd.[30] Bartel Leendert van der Waerden, Hans Freudenthal und André Weil traten Ungurus Thesen entgegen.[31][32][33]
Bei den Pythagoreern[Bearbeiten | Quelltext bearbeiten]
Viele Beziehungen über Zahlenfolgen haben die Pythagoreer durch Legen von Rechen- bzw. Spielsteinen gewonnen. Darunter fielen auch Varianten der binomischen Formeln, wie etwa[34]
Bereits Aristoteles spricht in seiner Metaphysik davon, dass „gewisse Leute Zahlen in die Gestalt von Dreiecken und Rechtecken bringen“.[35]

Eng verwandt ist die Beobachtung der Pythagoreer, dass sich die Quadratzahlen als aufsteigende Summen der ungeraden Zahlen ergeben:[36]
usw. Aus heutiger Perspektive werden solche Beobachtungen meist über vollständige Induktion rigoros bewiesen.[37] Ist etwa bereits bekannt, dass
gilt, so folgt mit der ersten binomischen Formel
und die Behauptung muss, da sie nach Annahme für stimmt, auch für stimmen. Da sie initial für richtig ist, muss sie folglich für alle natürlichen wahr sein.[38][39]
Die binomischen Formeln finden sich auch bei Nikomachos von Gerasa. Seine Einführung in die Arithmetik gilt als das älteste Buch der Antike, das speziell der Arithmetik gewidmet ist. Daneben existiert noch die Arithmetik des Diophantos, doch dieses Werk galt im Mittelalter als unbekannt. Nikomachos’ Werk hatte in den folgenden Jahrhunderten für die Arithmetik eine ähnliche Bedeutung wie Euklids Elemente für die Geometrie. Sie wurde von Boethius in seinem Werk De institutione arithmetica ins Lateinische übersetzt[40] und damit während des Mittelalters in Klosterschulen und Universitäten populär. Für ihn galt die dritte binomische Formel
als „wertvoll“, etwa zur schnellen Berechnung von Quadratzahlen:[41]
mit und
Bei Diophantos von Alexandria[Bearbeiten | Quelltext bearbeiten]
Auch Diophantos von Alexandria (zwischen 100 v. Chr. und 350) waren die binomischen Formeln geläufig. So hatte er unter anderem Kenntnis von den Identitäten[42]
und
Indien[Bearbeiten | Quelltext bearbeiten]
Bereits zwischen 400 v. Chr. und dem 2. Jahrhundert soll Pingala den Aufbau des Pascalschen Dreiecks bestimmt haben. Dieses listet die Binomialkoeffizienten schematisch auf. Dass er allerdings auch um den Zusammenhang zum binomischen Lehrsatz wusste, gilt nicht als plausibel.[43]
Im 6. und 7. Jahrhundert gaben die indischen Mathematiker Aryabhata und Brahmagupta die Fälle und an.[44] Der Ausdruck
wird auch als kubische binomische Formel bezeichnet.[45] Ferner zeigte Brahmagupta in seiner Brahmasphutasiddhanta die zu den binomischen Formeln verwandte Brahmagupta-Identität
die in der elementaren Zahlentheorie, zum Beispiel im Umfeld des Zwei-Quadrate-Satzes, eine Rolle spielt. Diese Identität lässt sich allerdings bereits in der Arithmetica von Diophantos von Alexandria finden und wurde zuerst von Leonardo von Pisa bewiesen.[46]
Narayana Pandit (circa 1325–1400) beschäftigte sich im Kapitel XI seiner Ganita Kaumudi unter anderen mit Primfaktorzerlegungen. Neben dem ausschöpfenden Dividieren von Zahlen durch die Primzahlen 2, 3, 5 usw. (was schon lange bekannt war) formuliert er einige Regeln zur Bestimmung von Zahlen und mit und der dazugehörigen Faktorisierung im Falle eines Erfolgs, die sich aus der dritten binomischen Formel ergibt. Damit nahm er die Grundidee des heute als Faktorisierungsmethode von Fermat genannten Prinzips vorweg. Als Beispielrechnung gibt er an:[47]
Blütezeit des Islam[Bearbeiten | Quelltext bearbeiten]
Bereits al-Chwarizmi beschäftige sich um das Jahr 830 mit geometrischen Lösungsverfahren linearer und quadratischer Gleichungen und folgte dabei sowohl indischen als auch griechischen Vorbildern, wobei letztere überwiegen. Dabei fanden auch neue Figuren als jene bei Euklid Einzug in seine Betrachtungen. Etwa bezieht sich auf in den Bildern 1 und 2, denn dann ist (siehe Bild 1) bzw. (siehe Bild 2).[48]
-
Bild 1:
-
Bild 2:
Bei al-Karadschi und noch deutlicher bei as-Samaw’al (1130–1180) finden sich Überlegungen, die wesentliche Schritte zu einem Beweis für den binomischen Lehrsatz, der die erste und zweite binomische Formel umfasst, durch vollständige Induktion enthalten. Dies bereitete Schwierigkeiten, da die mathematischen Ausdrucksmöglichkeiten der damaligen Zeit nicht ausreichten, eine derart allgemeine Aussage auch nur zu formulieren. Für die Berechnung der Binomialkoeffizienten verwendeten al-Karadschi und as-Samaw’al dabei – lange vor Blaise Pascal – das Pascalsche Dreieck.[49][50]
Der persische Mathematiker und Dichter Omar Chayyām (1048–1131) entwickelte eine Technik, um -te Wurzeln zu ziehen. Obwohl sein Werk verloren ging, wird davon ausgegangen, dass er den Umgang mit den allgemeinen binomischen Formeln beherrschte und auch die Binomialkoeffizienten in Form des Pascalschen Dreiecks kannte. Diese wurden in Europa erst 500 Jahre später durch Blaise Pascal wiederentdeckt.[51] Der Fall der Potenz 2 ist in Euklids Elementen explizit angegeben, und der Fall von höchstens Potenz 3 wurde von indischen Mathematikern aufgestellt. Chayyām erkannte somit als einer der ersten Mathematiker die Bedeutung eines allgemeinen binomischen Lehrsatzes. Er machte zudem die dreieckige Anordnung der Binomialkoeffizienten im Iran populär, sodass diese heute gelegentlich auch als Omar Chayyāms Dreieck bezeichnet wird.[52]
Renaissance und Moderne[Bearbeiten | Quelltext bearbeiten]
„Obwohl diese Behauptung eine unendliche Zahl an Fällen umfasst, werde ich einen ziemlich kurzen Beweis angeben, allein durch die Annahme zweier Lemmata.“


Mit diesen Worten eröffnete Blaise Pascal im Jahr 1654 einen der ersten niedergeschriebenen Induktionsbeweise. Ziel war es, den Term zu expandieren. Die ersten Ergebnisse lauten dabei[54]
- (siehe leeres Produkt)
usw. und Pascal erkannte ein Muster in den „Binomialkoeffizienten“:
usw. Die erste binomische Formel ist in rot dargestellt. Über Bildung von benachbarten Quotienten erhielt Pascal das alternative Dreieck[55]
usw. (exemplarisch in blau: es bezieht sich auf und im oberen Dreieck), mit dessen Hilfe er induktiv auf eine geschlossene Formel für die Zahlen im oberen Dreieck schließen konnte:[56]
„Das erste [Lemma], das selbstverständlich ist, sagt aus, dass dieses Verhältnis für die zweite Zeile eintritt, denn es ist ziemlich offensichtlich, dass sich […] verhält wie 1 zu 1. Das zweite besagt, dass, wenn dieses Verhältnis in irgendeiner Zeile auftritt, es auch in der nächsten Zeile notwendigerweise auftreten muss.“
In der modernen Mathematik wird – ganz im Sinne Pascals – gewöhnlich kein separates Studium der „binomischen Formeln zweiten Grades“ vollzogen, sondern stets der allgemeine binomische Lehrsatz für Terme genutzt. In manchen Lehrbüchern wird die durch den binomischen Lehrsatz gegebene allgemeine Formel für sogar auch als „binomische Formel“ bezeichnet.[57] Der Ausdruck „erste binomische Formel“ für den Fall im binomischen Lehrsatz ist jedoch bis heute in der Schulmathematik etabliert.[1]
Auftreten und Anwendungen[Bearbeiten | Quelltext bearbeiten]
Da es sich bei den binomischen Formeln um Identitäten handelt, die sich aus einer simplen Anwendung des Distributivgesetzes ergeben, sind ihre Anwendungen in der Mathematik theoretisch unbegrenzt, da sie in einer nicht endenden Anzahl von Rechnungen „auftauchen können“. Allerdings findet das Konzept der Identität von etwa und in einigen Bereichen, wie zum Beispiel der Wahrscheinlichkeitstheorie, eine bestimmte Interpretation. Dies wird dann deutlich, wenn die Identität über ihre bloß formale Existenz und Funktionstüchtigkeit hinaus eine Form der Information oder Erkenntnis preisgibt. Ferner existieren einige mathematische Standardsituationen, wie das Lösen quadratischer Gleichungen und Vereinfachen von Bruchtermen, bei denen die binomischen Formeln regelmäßig herangezogen werden.
Bruchrechnung[Bearbeiten | Quelltext bearbeiten]
Einige Brüche können mit den binomischen Formeln vereinfacht werden. In erster Linie handelt es sich um Brüche, die Quadratwurzeln in ihren Nennern haben. Dies kann anhand eines Beispiels demonstriert werden:
- .
Es wurde also durch Erweitern mit dem Faktor und Anwenden der dritten binomischen Formel der Nenner vereinfacht, und die Quadratwurzeln in den Zähler „transportiert“. Dieses Prinzip ist ein Spezialfall der sogenannten Rationalisierung von Brüchen.[58]
Eine andere Anwendung betrifft die Vereinfachung von Bruchtermen. Dabei können die binomischen Formeln manchmal dabei helfen, Nenner und/oder Zähler des Bruchs zu faktorisieren, um anschließend ein Kürzen des Bruchs zu ermöglichen. Ein Beispiel unter Nutzung der dritten binomischen Formel ist[59]
Ein anderes Beispiel betrifft die zweite binomische Formel:
- .
Näherungen[Bearbeiten | Quelltext bearbeiten]
Mit Hilfe der binomischen Formeln können manche eher komplizierten Ausdrücke schnell durch deutlich leichtere Terme geschätzt werden. So gilt für kleine Werte [60]
Anwendungsbeispiele sind
- (exakt gilt )
und
- (exakt gilt )
Die Begründung dieser Näherung ergibt sich aus der Näherung
- (beachte: Ist klein, so erst recht z. B. ist der zehnte Teil eines Zehntels nur ein Hundertstel, also ),
und anschließende Division durch Je kleiner hier ist, desto kleiner ist der relative Fehler. Auf ähnliche Weise erhält man über die erste binomische Formel für kleine Werte
also[61]
Diese Näherungsformeln können mittels Taylor-Polynomen weiter verbessert werden.[62] Gleichzeitig ist die erste binomische Formel damit Ausgangspunkt[63] für das sogenannte Heron-Verfahren zur Annäherung von Quadratwurzeln, das die oberen Annäherungen iterativ benutzt.[64][65]
Quadratische Ergänzung und Herleitung der Mitternachtsformel[Bearbeiten | Quelltext bearbeiten]
Es ist
ein Beispiel für eine wahre Gleichung: Beide Zahlen auf jeder Seite des Gleichheitszeichens sind identisch. Gleichungen können umgeformt werden. Dahinter steckt die Idee, dass, wenn zwei identische Größen auf identische Weise manipuliert werden, die Resultate wieder identisch sein müssen. Aus beidseitiger Addition von mit geht hervor – wieder eine gültige Gleichung. Oft beinhalten Gleichungen eine Unbekannte, etwa Beidseitige Division durch formt dies zu um, womit die Unbekannte plötzlich „sichtbar“ wird. Im Nachhinein ist auch der einfache Zusammenhang leicht zu prüfen, und es war der „einzige Kandidat“, der mit schon unausweichlich bestimmt war. In vielen Problemen der wissenschaftlichen Praxis entstehen aus bekannten Beziehungen zunächst unbekannter Größen Gleichungen, weshalb Techniken zu deren Auflösen große Bedeutung zukommt. Die innerhalb einer wissenschaftlichen Theorie erarbeiteten kausalen Zusammenhänge oder ökonomische Forderungen „zwingen“ die Größen in einen begrenzten Raum an Möglichkeiten, doch erst ein Auflösen der entstehenden Gleichungen macht diese wenigen Möglichkeiten „sichtbar“.
Ein Beispiel ist: Ein rechteckiges Zimmer ist zwei Meter länger als breit und hat den Flächeninhalt Quadratmeter – wie lang und wie breit ist es? Die Frage führt zur Gleichung
- ( = Breite des Zimmers in Metern),
also
Dies ist Beispiel einer quadratischen Gleichung. Gerade im Umgang mit quadratischen Gleichungen erweisen sich die binomischen Formeln als nützlich. Die Grundidee ist, „umgekehrt“ zu denken: Schafft man es, irgendwo einen Term der Form zu erzeugen, kann eine Gleichung vereinfacht werden. Dies erfordert ein gewisses Geschick beim „Erkennen“ und zu Beginn meist etwas Übung. Im obigen Beispiel kann auf der linken Seite durch Hinzufügen eines nichtigen Terms wie folgt eine binomische Formel „erzwungen“ werden:
Nun muss nur noch auf beiden Seiten die Quadratwurzel in beiden Zweigen gezogen werden (was letztlich der entscheidende Schritt zum „Auflösen“ der Gleichung ist), um aus
die Lösungsmenge zu erhalten. Damit hat das Zimmer die Breite .[Anm. 2] Dies war schon seit Aufstellung der Bedingungen an das Zimmer „unausweichlich“, wurde aber erst nach Auflösung der quadratischen Gleichung für Geist und Auge „sichtbar“.
Eben dieses Prozedere der Erzeugung eines Terms passend zur ersten (oder auch zweiten) binomischen Formel nennt man auch quadratische Ergänzung.[66]
Tatsächlich kann genau dieses Verfahren zur Herleitung der allgemeinen „Mitternachtsformel“ genutzt werden, wobei die Idee durch das obige Beispiel bereits vollständig beschrieben ist und lediglich unter Verwendung allgemeiner „Platzhalter“ in ausgeführt werden muss.[67][68]
Beweis des Satz des Pythagoras[Bearbeiten | Quelltext bearbeiten]

Der Satz des Pythagoras ist einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen rechtwinkligen Dreiecken die Summe der Flächeninhalte der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates ist. Sind also und die Längen der am rechten Winkel anliegenden Seiten, der Katheten, und die Länge der dem rechten Winkel gegenüberliegenden Seite, der Hypotenuse, dann lautet der Satz als Gleichung ausgedrückt:
Mehr noch werden durch diesen Satz die rechtwinkligen Dreiecke charakterisiert. Ist das betrachtete Dreieck also nicht rechtwinklig, kann die Gleichung nicht erfüllt sein.
Der Satz des Pythagoras kann mit Hilfe der ersten binomischen Formel bewiesen werden.[69][70] Hintergrund ist eine einfache geometrische Idee: In ein Quadrat mit der Seitenlänge werden vier kongruente rechtwinklige Dreiecke mit den Seiten und (Hypotenuse) eingelegt. Dies kann auf zwei Arten geschehen, wie im Diagramm dargestellt ist.
-
Graphik P: Der Satz des Pythagoras ergibt sich aus der Betrachtung derselben Fläche (hier in Weiß) aus unterschiedlichen Perspektiven: Einmal als und einmal als Mit Hilfe der ersten binomischen Formel kann diese Idee rigoros gemacht werden.
Um diese geometrische Idee algebraisch rigoros zu machen, werden Termumformungen benötigt, bei denen die erste binomische Formel von Nutzen ist. Die Gesamtfläche des Quadrates ist einerseits wegen der ersten binomischen Formel

Der Mittelterm entspricht den Flächen der vier kongruenten Dreiecke in Graphik P; jedes einzelne mit Fläche siehe Graphik R. Andererseits kann die Fläche des großen Quadrates als Summe der – in Graphik P weißen – Fläche und erneut der Fläche der vier Dreiecke dargestellt werden:
Dies entspricht dem oben erwähnten „Perspektivwechsel“: Der Term ist in beiden Ausdrücken zu finden, da die vier Dreiecke im linken Bild von Graphik P bloß verschoben werden. Da es sich in beiden Fällen um die selbe Ausgangsfläche handelte, gilt folglich
Zieht man nun auf beiden Seiten ab, verbleibt was genau der Satz des Pythagoras ist.
Als Anwendung des Satzes des Pythagoras ergibt sich, wieder unter Anwendung der ersten binomischen Formel, ein Beweis des Höhensatzes von Euklid.[71]
Die Hardy-Weinberg-Formel[Bearbeiten | Quelltext bearbeiten]
Eine Anwendung der ersten binomischen Formel betrifft die Hardy-Weinberg-Formel. Von nahezu allen Genen gibt es unterschiedliche Varianten, die als Allele bezeichnet werden. So kann es etwa verschiedene Allele für die Farbe einer Linsensorte geben, für die Größe von Individuen, aber auch für bestimmte Proteine, die im Stoffwechsel eine tragende Rolle spielen.
Den Anteil, mit der ein solches Allel in einer Population vorkommt, nennt man Allelfrequenz. Im einfachsten Fall gibt es nur zwei Allele, also zwei Genvarianten, die zum Beispiel als und bezeichnet werden können. Für die entsprechenden Allelfrequenzen und gilt dann Nun trägt jedes Individuum von einem bestimmten Gen zwei Stück, eines vom Vater, eines von der Mutter. Eine Ausnahme von dieser Regel sind lediglich bestimmte geschlechtsgebundene Gene (siehe auch X-chromosomaler Erbgang). Man erhält dann, unter Annahme einer perfekten Durchmischung der betrachteten Population, die Hardy-Weinberg-Formel
Wird nun angenommen, das Allel A sei dominant, bedeutet dies, dass die Merkmale von Allel bei der Genkombination nicht erkenntlich sind, sondern nur bei Die von getragenen Merkmale nennt man dann rezessiv. Sind beispielsweise vier Prozent einer Population Merkmalsträger von so ist die Allelfrequenz von höher als gedacht: Die Hardy-Weinberg-Formel liefert und damit Demzufolge ist und immerhin Ergo sind 32 Prozent der Bevölkerung Träger des Allels ohne aber Merkmalsträger zu sein.[72]
Wahrscheinlichkeitstheorie und Statistik[Bearbeiten | Quelltext bearbeiten]

In eine ähnliche Richtung wie die Hardy-Weinberg-Formel geht folgende probabilistische Interpretation der ersten binomischen Formel. Diese hängt mit der zweifachen Ausführung eines Zufallsexperiments mit unabhängigen Abläufen (zum Beispiel dem zweifachen Wurf einer Münze) zusammen. Stehen sich in einem Zufallsexperiment zwei mögliche Ausgänge gegenüber, etwa „Gewinnen“ und „Verlieren“, so folgt für deren Wahrscheinlichkeiten und bereits (die Eins entspricht hier ), da bei angenommenem Ausschluss eines Unentschiedens eines dieser Ereignisse sicher eintritt. Zweifache Ausführung führt zu folgender neuen „Aufteilung der Eins“:
Dies bildet die möglichen – sich gegenseitig ausschließenden – Ereignisse
- „zweimal gewinnen“ (mit Wahrscheinlichkeit ),
- „je einmal gewinnen und verlieren“ (mit Wahrscheinlichkeit – es wird bei diesem Ereignis nicht in der Reihenfolge, also zwischen und unterschieden![Anm. 3]) und
- „zweimal verlieren“ (mit Wahrscheinlichkeit )
ab.[73] Auf diese Weise werden die Wahrscheinlichkeiten und als „Teilvolumina der Eins“ sichtbar (siehe Bilder unten). Ist beim zweifachen Münzwurf zum Beispiel so trifft Kopf-Kopf und Zahl-Zahl jeweils mit den Wahrscheinlichkeiten auf, und „je einmal Kopf und einmal Zahl“ mit der Wahrscheinlichkeit
-
K = „Kopf“, Z = „Zahl“. Darstellung des zweifachen Münzwurfs mittels eines Baumdiagramms. Eine einfache Regel besagt, dass sich bei unabhängigen Abläufen die Wahrscheinlichkeiten „entlang der Äste“ multiplizieren. In diesem Spezialfall ergibt sich dies aus der ersten binomischen Formel, siehe Bilder rechts.
-
Wahrscheinlichkeiten sind Konzepte der Maßtheorie und können damit als „Teilvolumina“ des „Ganzen mit Volumen Eins“ gesehen werden.[74] Sie messen Plausibilität. Um Zahl-Zahl zu werfen, muss „die Hälfte einer Hälfte“ getroffen werden, also ein Viertel. Analog: Triff an jeder Seite des Quadrats die „richtige Hälfte“ (für Zahl-Zahl hier „rechts“ und „unten“), was dann zur gezeigten Aufteilung in Flächen führt, und in diesem Fall alle vier Möglichkeiten gleich plausibel macht.
-
„Wahrscheinlichkeiten und Geometrie“: Analoge Situation für allgemeine Einzelwahrscheinlichkeiten (hier exemplarisch und ). Das ganze Quadrat hat „Volumen“ Eins. Die erste binomische Formel gibt exakt die Einzelwahrscheinlichkeiten nach zweifacher Ausführung des Experiments, geometrisch realisiert durch Teilflächen. In diesem Beispiel ist das Ereignis BB (mit Wahrscheinlichkeit ) viermal weniger plausibel als AA (mit ).
Diese Verfahren lassen sich ganz analog auf beliebig häufige Wiederholungen von zum Beispiel Münzwürfen ausweiten, wobei dann der binomische Lehrsatz zur Expansion von für beliebige natürliche Zahlen eine wichtige Rolle spielt. Man spricht dann, hinsichtlich der auftretenden Wahrscheinlichkeiten, von der Binomialverteilung.[75]
Die zweite binomische Formel findet auch unmittelbare Anwendung in der Stochastik, nämlich bei der Berechnung der Varianz einer Zufallsvariablen. Diese misst ab, wie stark eine Zufallsvariable um ihren Erwartungswert (= Mittelwert) gestreut ist. Um Ausreißer stärker zu „bestrafen“ und Vorzeichen zu ignorieren, wird dabei das Quadrat der Abweichung gemessen, also wiederum dessen Erwartungswert berechnet. Mit der zweiten binomischen Formel kann dies zusammen mit der Linearität des Erwartungswertes vereinfacht werden:[76]
Die Varianz kann also als Differenz zwischen dem „erwarteten Quadrat“ und dem „Quadrat des Erwarteten“ gesehen werden. In dieser neuen Darstellung entpuppt sie sich als Fehlerterm in der Cauchy-Schwarz-Ungleichung die in Hilberträumen mit Skalarprodukt gültig ist, und sich für Erwartungswerte in übersetzt. Damit erhält die Varianz eine geometrische Interpretation. Es wird über den Fehler in der Ungleichung gemessen, wie weit von einer konstanten Funktion (also ohne jegliche Abweichung, ergo „Varianz Null“), entfernt ist.
Differentialrechnung[Bearbeiten | Quelltext bearbeiten]
Die Differentialrechnung beschäftigt sich mit dem Änderungsverhalten mathematischer Funktionen. In vielen Anwendungen ist eine Funktion eine Abbildung, die jedem Zeitpunkt (etwa ab „Beginn der Aufzeichnung“) einen für die Anwendung interessanten Ausgabewert zuordnet; dies kann zum Beispiel
- eine beim Laufen zu einer Uhrzeit bereits zurückgelegte Distanz,
- die aktuelle Temperatur des Kaffees im Arbeitszimmer oder
- der momentane Preis für einen Liter Benzin (etwa in „Cent pro Liter“)
sein. Die Ableitung einer solchen Funktion misst dann die Änderungsraten, also wie schnell sich der Bestand aktuell mit der Zeit ändert. Bezogen auf die oberen Beispiele bedeutet dies
- die momentane Laufgeschwindigkeit,
- die momentane Abkühlungsrate des Kaffees,
- die Preisänderungsrate (etwa in „Cent pro Liter pro Stunde“).
Während der höheren mathematischen Ausbildung werden Ableitungsregeln vermittelt, die das Ableiten einer möglichst großen Klasse elementarer Funktionen ermöglichen sollen, um ein breites Anwendungsspektrum zu bedienen. Diese Regeln basieren allesamt auf dem Grundkonzept der Ableitung, dem Differentialquotienten. Die Idee dahinter ist, aus den bekannten Beständen, also der Ursprungsfunktion, die Veränderungsraten direkt zu berechnen. In vielen Lehrtexten wird die Ableitung der quadratischen Funktion als Standardbeispiel zur Erläuterung des Differentialquotienten herangezogen, wobei die erste binomische Formel das entscheidende Hilfsmittel ist.[77][78][79] Für die gesuchte Ableitungsfunktion gilt und die rührt von der ersten binomischen Formel her.
-
Veränderung kann zu unterschiedlichen Zeitpunkten anders sein. Je steiler die Kurve, desto größer die momentane Änderungsrate des Arbeitseifers mit der Zeit. Die Ableitung entspricht geometrisch der Tangentensteigung an der Kurve.
-
Graphische Darstellung der Approximation von durch Letztere ist die Tangente von an der Stelle Durch dieses Prinzip kann der Normalparabel an der Stelle die „Steigung 2“ zugeordnet werden, da der Begriff der Steigung für lineare Funktionen erklärt ist. Der Wert der Steigung berechnet sich schlicht aus der Ableitungsfunktion
Steht etwa für die Strecke in Metern, die ein Partikel zum Zeitpunkt (in Sekunden) zurückgelegt hat, und möchte man dessen Geschwindigkeit zu einem festgelegten Zeitpunkt ermitteln, müssen die Differenzen studiert werden. Dahinter steckt der Gedanke, dass sich aus Differenzen Veränderungen berechnen lassen. Da das Partikel beispielsweise nach Sekunden schon und nach Sekunden bereits Meter zurückgelegt hat, hat es im Zeitraum zwischen zwei und drei Sekunden insgesamt Meter zurückgelegt. Es ist also allgemein nach Funktionsvorschrift unter Anwendung der ersten binomischen Formel
der Streckenzuwachs im Zeitintervall von bis [80] Um daraus die durchschnittliche Geschwindigkeit zu ermitteln, muss noch durch den Zeitraum dividiert werden, also Damit ergibt sich[81]
Lässt man den Zeitraum gegen Null gehen, wird daraus eine momentane Geschwindigkeit, und diese ist zum Zeitpunkt exakt Meter pro Sekunde. Das Partikel bewegt sich mit der Zeit also zunehmend schneller, erfährt also wegen der sogar quadratischen Zunahme seiner Distanz eine Beschleunigung. Wird vom Luftwiderstand abgesehen, erfahren fallende Gegenstände in Richtung Erdoberfläche eine derartige Beschleunigung (siehe Bild): Die zurückgelegte Distanz nach Sekunden des freien Falls beläuft sich auf mit der Normfallbeschleunigung Meter pro Sekunde zum Quadrat.
Die bekannte Regel für natürliche Zahlen lässt sich genau analog unter Einsatz des allgemeineren binomischen Lehrsatzes nachweisen.[82]
Auch andere Differentialquotienten lassen sich mit binomischen Formeln direkt berechnen. Etwa folgt für die Wurzelfunktion für mit der dritten binomischen Formel[83]
also
Fermats Faktorisierungsmethode und Kryptographie[Bearbeiten | Quelltext bearbeiten]

Das RSA-Kryptosystem basiert auf folgender Idee: Eine Person, zum Beispiel Alice, möchte eine private Nachricht an ihren Freund Bob versenden. Um sicher zu gehen, dass kein Dritter die Nachricht lesen kann, erzeugt der Empfänger Bob zuvor einen Schlüssel. Dieser Schlüssel besteht aus zwei Komponenten: Dem öffentlichen Schlüssel und dem privaten Schlüssel. Wie es die Namen schon andeuten, verfährt Bob nun wie folgt:
- Veröffentlichung des öffentlichen Schlüssels, zum Beispiel zum freien Download auf seiner Website.
- Geheimhaltung des privaten Schlüssels, etwa auf einer Festplatte außer Reichweite des Internets (oder wiederum verschlüsselt auf seinem PC).
Die beiden Schlüsselkomponenten „passen exakt zusammen“: Nutzt Alice den öffentlichen Schlüssel, um aus einem Klartext einen Geheimtext (in Form von „Buchstabensalat“) zu erzeugen, so ist nur der private Schlüssel von Bob in der Lage, dies in schneller Zeit wieder zu entwirren. Das Kryptosystem ist nur dann sicher, wenn ein Angreifer nicht in der Lage ist, in vernünftiger Zeit aus dem öffentlichen Schlüssel den privaten Schlüssel auszurechnen. Der große Vorteil dieser asymmetrischen Kryptosysteme besteht darin, dass sich Alice und Bob nicht zum Schlüsselaustausch persönlich treffen müssen.
Im Falle des RSA-Kryptosystems basiert die Generierung von öffentlichem und privatem Schlüssel auf dem Faktorisierungsproblem. Dafür werden zwei Primzahlen und benötigt. Im Anschluss werden diese zu einer Zahl multipliziert. Ist beispielsweise und (also Größenordnung 1,3 Milliarden), so gilt
Dieses Prozedere kann innerhalb vernünftigen Zeitaufwands theoretisch sogar per Hand erfolgen. Das umgekehrte Problem, hier exemplarisch die Faktorisierung von
in seine (zwei) Primfaktoren, ist ohne vorheriges Wissen um hingegen im Allgemeinen ein extrem schwieriges Problem.[84] Haben die Primzahlen je ein paar hundert Stellen, ist es selbst durch die Supercomputer der heutigen Zeit nicht in vernünftiger Zeit zu lösen (bis auf Sonderfälle, siehe unten). Aus den Primzahlen und kann nun ein öffentlicher und privater Schlüssel erstellt werden, wobei das Produkt ein Teil des öffentlichen Schlüssels ist. Deshalb gleicht das Bilden des Produkts gewissermaßen dem „Zuschnappen einer Sicherheitstür“, denn ein Angreifer müsste und aus berechnen, um an den privaten Schlüssel zu gelangen. Für die Sicherheit des Verfahrens notwendig (jedoch im Allgemeinen nicht hinreichend, es müssen weitere Details beachtet werden),[85] sind unter anderem, dass
- die Primzahlen und groß genug sind (einige hundert Stellen, der Primzahlsatz garantiert dann einen Möglichkeitenpool größer als die geschätzte Anzahl der Atome im Universum)
- und nicht zu nahe beieinander liegen.[86]
Der Grund für die zweite Einschränkung liegt in der Faktorisierungsmethode von Fermat, deren Idee auf der dritten binomischen Formel beruht.[87][88] Ist
für ganze Zahlen so gilt die Faktorisierung
Liegen die Primzahlen und nahe beieinander, so ist die Differenz im Verhältnis zu und sehr klein. Damit ist in der Faktorisierung deutlich größer als und kann durch gut geschätzt werden. In obigem Beispiel liegen die Primfaktoren äußerst nahe beieinander,
weshalb das Kryptosystem hier schnell geknackt werden kann: Es gilt[Anm. 4]
Damit schätzt man durch Aufrunden und überprüft, ob als eine Differenz für eine kleine Quadratzahl geschrieben werden kann, also kurz Man erhält
womit die Primzahlen und und damit die Faktorisierung schnell gefunden ist. Mit dem Wissen um und kann ein Angreifer nun den privaten Schlüssel aus dem öffentlichen Schlüssel berechnen, und die Nachrichten von Alice an Bob nach Abfangen mitlesen.[89]
Irrationalität der Quadratwurzel aus 2[Bearbeiten | Quelltext bearbeiten]
Die Quadratwurzel aus 2 ist jene positive reelle Zahl, deren Quadrat den Wert hat; mit anderen Worten, die mit sich selbst multipliziert ergibt. Die ersten Dezimalstellen sind gegeben durch
Die binomischen Formeln können für einen Beweis genutzt werden, dass eine irrationale Zahl ist. Damit ist gemeint, dass nicht als Verhältnis zweier ganzer Zahlen dargestellt werden kann. Es gilt also für alle natürlichen Zahlen und Dies ist gleichbedeutend damit, dass die oben angedeutete Dezimalentwicklung keinem periodischen Muster unterworfen ist, wie es bei rationalen Zahlen, etwa der Fall ist.
Der Beweis kann durch Widerspruch geführt werden. Das heißt, man geht davon aus, es gäbe eine Bruchdarstellung mit irgendwelchen natürlichen Zahlen und und führt diese Annahme zu einem Widerspruch. Jeder Bruch lässt sich vollständig kürzen, also kann davon ausgegangen werden, dass der Nenner minimal ist. Zum Beispiel wäre in diesem Sinne „“ keine minimale Darstellung, nach weiterer Kürzung mit sehr wohl aber „“. Für den darstellenden Bruch ist folgende Beobachtung sehr wichtig: Da ist, gilt womit
- und
folgt. Die Differenz aus Zähler und Nenner des Darstellungsbruchs ist also kleiner als der als minimal angenommene Nenner Mit der Eigenschaft folgt nun mittels zweifacher Anwendung der zweiten binomischen Formel:
Ergo hat man
was wegen der Observation der Minimalität des Nenners widerspricht. Anschaulich wäre also ein „Bruch, der sich unendlich oft kürzen lässt“, und einen solchen kann es nicht geben.[90]
Ungleichungen[Bearbeiten | Quelltext bearbeiten]
Mit den binomischen Formeln können diverse Ungleichungen gezeigt werden.
Die Dreiecksungleichung zählt zu den grundlegendsten und bedeutendsten Ungleichungen der Mathematik, mit vielfältigen Anwendungen zum Beispiel in Analysis und Geometrie. In ihrer einfachsten Form besagt sie: Für beliebige reelle Zahlen und gilt
Hierbei steht für den Absolutbetrag. Sie kann auf unterschiedliche Weise bewiesen werden. Eine davon nutzt die erste binomische Formel: Hierfür werden als zusätzliche Hilfsmittel lediglich die Regeln und [91] benötigt. Es gilt damit
womit die Dreiecksungleichung nach Ziehen der (positiven) Quadratwurzel auf beiden Seiten folgt.[92] Dabei ist zu beachten, dass die Wurzelfunktion monoton steigt, also für äquivalent zu ist.
Mit der zweiten binomischen Formel ergibt sich die für reelle Zahlen gültige Ungleichung
Bezeichnet wird diese auch als binomische Ungleichung.[1] Sie ergibt sich aus[93]
Gleichheit gilt genau dann, wenn Die binomische Ungleichung ist ein Spezialfall der allgemeineren Young-Ungleichung[1] und der Ungleichung zwischen arithmetischen und geometrischen Mittel.[94] Eine Anwendung der binomischen Ungleichung ist, dass bei zweifacher unabhängiger Wiederholung eines Glücksspiels mit den möglichen Ausgängen „gewinnen“ und „verlieren“ bei ungleichen Wahrscheinlichkeiten das gemischte Ergebnis „einmal gewinnen und verlieren“ unwahrscheinlicher ist als das Ereignis entweder „doppelt gewinnen“ oder „doppelt verlieren“.
Rechnen mit komplexen Zahlen[Bearbeiten | Quelltext bearbeiten]
Die komplexen Zahlen erweitern den Bereich der reellen Zahlen derart, dass die zuvor nicht lösbare Gleichung lösbar wird. Dies geschieht über die Einführung einer „neuen Zahl“, der sogenannten imaginären Einheit mit der Eigenschaft Eine beliebige komplexe Zahl kann stets in der Form geschrieben werden, wobei und reelle Zahlen sind. Beispiele sind oder aber auch jede beliebige reelle Zahl ist eine komplexe Zahl.[95] Es kann etwa der Ausdruck nicht weiter vereinfacht werden, da die grundlegenden Größen und über keine gemeinsame „Zählbasis“ verfügen (mit anderen Worten, da für keine reelle Zahl sein kann).[96]
Das Rechnen mit komplexen Zahlen funktioniert genauso wie das mit reellen Zahlen, wobei die hauptsächliche Neuheit im Umgang mit der imaginären Einheit besteht. Besonders der Einsatz der dritten binomischen Formel ist in vielen Situationen hilfreich. Zum Beispiel gilt wegen
Damit können Divisionen vollzogen werden:
Das Ergebnis ist jetzt wieder in der Standardform für komplexe Zahlen.[97]
Trigonometrie[Bearbeiten | Quelltext bearbeiten]
Identitäten[Bearbeiten | Quelltext bearbeiten]

Durch bzw. wird der Kreis mit Radius 1 und Mittelpunkt im Ursprung in der reellen bzw. komplexen Ebene parametrisiert. Der Satz des Pythagoras ist gleichbedeutend mit [98]
Die binomischen Formeln sind Hilfsmittel bei der Herleitung wichtiger Identitäten zwischen Sinus und Kosinus. Als entscheidende Zutat wird dabei zusätzlich die Eulersche Formel
gebraucht, die unter Einsatz komplexer Zahlen einen weitreichenden Zusammenhang zwischen der natürlichen Exponentialfunktion und den Winkelfunktionen herstellt. Man hat dann
aber wegen der immer gültigen Relation unter Benutzung der ersten binomischen Formel[99]
Durch Vergleich von Real- und Imaginärteil ergeben sich damit die sogenannten Verdoppelungsformeln[100][101]
Unter Einsatz der dritten binomischen Formel ergibt sich zudem ein alternativer Beweis des Satz des Pythagoras über komplexe Zahlen:[102]
Parametrisierung des Kreises[Bearbeiten | Quelltext bearbeiten]
Mit der ersten und zweiten binomischen Formel erhält man, dass
den Einheitskreis in der xy-Ebene parametrisiert,[103] denn es gilt also mit den Rechenregeln für Brüche
Damit ergeben sich die Parameterdarstellungen
wobei die Beziehung zwischen Winkel und Parameter durch (mit dem Arkustangens) explizit gemacht werden kann.[104] Dies hat unmittelbare Anwendungen beim Auflösen trigonometrischer Integrale. Mittels
können Integrale wie etwa
durch Substitution, etwa auf lösbare Integrale über rationale Funktionen zurückgeführt werden.[105]
Algebra[Bearbeiten | Quelltext bearbeiten]
Bei der Faktorisierung von Polynomen in ein, zwei oder auch mehr Variablen können die binomischen Formeln in manchen Situationen angewendet werden. Beispiele sind[106]
und
aber auch
und
mit der imaginären Einheit
Zahlentheorie[Bearbeiten | Quelltext bearbeiten]
Pythagoräische Tripel[Bearbeiten | Quelltext bearbeiten]

Der Satz des Pythagoras besagt, dass in rechtwinkligen Dreiecken mit Katheten und Hypotenuse stets die Relation gilt. Die Frage nach sogenannten Pythagoräischen Tripeln hebt diese zunächst geometrische Aussage zusätzlich auf ein zahlentheoretisches Level. Die Frage ist, ob es zusätzlich möglich ist, die Seitenlängen des Dreiecks ganzzahlig zu wählen. Ein einfaches Beispiel ist das Tripel denn es gilt
siehe Bild. Ein Tripel ganzer Zahlen mit der Eigenschaft nennt man auch Pythagoräisches Tripel.
Mit Hilfe der binomischen Formeln gelingt eine Charakterisierung der Pythagoräischen Tripel. Dabei ist zunächst die Beobachtung nützlich, dass sich aus einem Pythagoräischen Tripel gleich unendlich viele weitere Tripel erzeugen lassen, indem man mit Quadratzahlen multipliziert. Multipliziert man zum Beispiel mit der Quadratzahl ergibt sich , bzw.
Daraus motiviert sich der Begriff des primitiven Pythagoräischen Tripels: Ein Tripel heißt primitiv, wenn der größte gemeinsame Teiler von und gleich ist, und es genügt, die primitiven Tripel zu bestimmen, da sich alle anderen Tripel auf solche reduzieren lassen. Es lässt sich unter Anwendung der ersten binomischen Formel zeigen, dass die primitiven Pythagoräischen Tripel genau durch
gegeben sind, wobei und teilerfremd und nicht beide ungerade sind.[107][108][109] Zum Beispiel gilt mit
Die primitiven Pythagoräischen Tripel korrespondieren zu den rationalen Punkten auf der algebraischen Kurve , also dem Einheitskreis. Sie zeigen auf, dass es unendlich viele rationale Punkte sind, denn es gibt unendlich viele primitive Pythagoräische Tripel. Jedes Tripel gibt aber einen rationalen Punkt, denn aus folgt zum Beispiel
Also sind rationale Punkte auf . Unter enormen Anstrengungen konnte 1995 durch Andrew Wiles und Richard Taylor gezeigt werden, dass die einzigen rationalen Punkte auf den Kurven mit die „trivialen Punkte“ sind, also solche, bei denen stets oder ist. Diese Aussage ist gleichbedeutend zum Großen Fermatschen Satz. Die „höheren binomischen Formeln“ (siehe auch binomischer Lehrsatz oder Multinomialtheorem) liefern also in den Fällen höherer Exponenten keine nicht-trivialen rationalen Punkte.[110]
Zerlegung in zwei Quadrate[Bearbeiten | Quelltext bearbeiten]
Eine Frage, welche die Zahlentheorie lange beschäftigte, war, ob sich eine gegebene natürliche Zahl als Summe zweier Quadratzahlen schreiben lässt, wie etwa
Eine solche Darstellung muss nicht eindeutig sein, so gilt zum Beispiel auch
Unmittelbar verwandt zu den binomischen Formeln ist die Identität von Diophantos:
Einsetzen von liefert zum Beispiel
Die Brahmagupta-Identität besagt[111]
Sind also zwei natürliche Zahlen als Summe zweier Quadrate darstellbar, so auch ihr Produkt. Als Folgerung des Zwei-Quadrate-Satzes weiß man heute, dass eine natürliche Zahl genau dann als Summe zweier Quadrate dargestellt werden kann, wenn sämtliche Primzahlen in ihrer Primfaktorzerlegung, mit der Eigenschaft, dass die Zahl teilt (kurz: ), in gerader Häufigkeit auftauchen.[112] Zum Beispiel lässt sich als Summe zweier Quadrate schreiben (), da die einzige Primzahl in der Zerlegung mit gerade ist, und diese in doppelter, ergo gerader Häufigkeit auftritt. Im Gegensatz dazu ist z. B. nicht Summe zweier Quadratzahlen.
Didaktik[Bearbeiten | Quelltext bearbeiten]
Binomische Formeln im Kontext der Schulalgebra[Bearbeiten | Quelltext bearbeiten]
Die Formelsprache der Algebra ist das zentrale Darstellungsmittel der Mathematik. Sie ist ein Zeichensystem, in dem vorhandenes Wissen über Zahlen und funktionale Zusammenhänge von Größen allgemein erfasst und kodiert, mit den dargestellten Beziehungen gedanklich operiert und damit neues Wissen erzeugt werden kann. Es existiert ein großes Spektrum an mathematischen Objekten, deren Beziehungen und Zusammenhänge in der Formelsprache dargestellt werden können. Gleiches gilt für inner- und außermathematische Situationen. Beispiele hierfür sind Flächen- und Volumenberechnungen in Abhängigkeit von z. B. Seitenlängen, aber auch die binomischen Formeln.[113]
Durch die gesamte Geschichte der Mathematik hinweg war die Algebra stets ein Werkzeug, um inner- und außermathematische Probleme zu lösen. Auch in der aktuellen Schulmathematik wird Algebra in diesem Sinn verwendet. Algebraische Denk-, Arbeits- und Darstellungsweisen sind essenziell für alle Teilbereiche der Schul- und Berufsmathematik. Sie treten bei der Mathematisierung von Problemen aus dem technischen, wirtschaftlichen oder gesellschaftlichen Bereich auf. Ferner sind sie über den Mathematikunterricht hinaus auch für andere Schulfächer von Bedeutung, vor allem für die Fächer Physik und Informatik.[114] Die binomischen Formeln sind dabei Bestandteil der elementaren Algebra und werden im Mathematikunterricht meist als besondere Formeln zur Umformung (beispielsweise Multiplikation) von Binomen verwendet. Ihr hauptsächlicher Zweck ist es, als Merkformeln eine Erleichterung für beispielsweise das Ausmultiplizieren oder Zusammenfassen von Klammerausdrücken zu bilden und eine Lösungsstrategie für das Faktorisieren von Termen bereitzustellen.[115] Sie gehören damit zu den wichtigsten Grundpfeilern der Schulmathematik.[116]

Nach allgemeiner Auffassung der mathematikdidaktischen Gemeinschaft gilt die „elementar-algebraische Formelsprache als ein grundlegendes Darstellungsmittel der Mathematik und gehört zu den klassischen Stoffgebieten an weiterführenden Schulen.“[118] In einem empirisch-orientierten Mathematikunterricht stehe gerade die Verbindung verschiedener Bereiche im Mittelpunkt, etwa für den Fall der binomischen Formeln die Verbindung der Terme und Formeln mit einer gegebenen (geometrischen) Sachsituation. Die aus der Grundschulzeit bekannten Grundrechenarten, von denen die Schüler durch die Einführung und den Umgang in der fünften Klasse eine geometrische Grundvorstellung ausgebildet haben, werden damit innerhalb von Sachsituationen auf das Rechnen mit Termen übertragen.[119][120]
Serge Lang, Autor zahlreicher Bücher zur Mathematik, beklagte, dass viele seiner Studenten „nicht in der Lage seien, Ausdrücke wie und augenblicklich auszumultiplizieren“. Als Ursache dieser „Schwächen in der elementaren Algebra“ verwies er auf „Defizite in der mathematischen Schulbildung“ in den USA.[121]
An deutschen Realschulen und Gymnasien werden die binomischen Formeln gewöhnlich spätestens ab der 8. Klasse thematisiert.[122][123][124] In der Schweiz sind sie Gegenstand der 7. bis 8. Klasse,[125] und in Österreich der 3. Klasse der Sekundarstufe I, siehe auch Sekundarbildung Unterstufe.[126] Jedoch bleiben sie auch nach ihrer Einführung in ständigem Gebrauch, etwa bei Anwendungen in der elementaren Geometrie (z. B. dem Satz des Pythagoras),[127] Umformungen von Termen, und im Kontext quadratischer Gleichungen.[128]
Häufig gemachte Rechenfehler und Fehleranalysen[Bearbeiten | Quelltext bearbeiten]
Ein häufiger Fehler in der mathematischen Ausbildung bei einer Anwendung der binomischen Formel ist, dass „Quadrat einer Summe“ mit „Summe der Quadrate“ gleichgesetzt wird.[129] Ein Beispiel ist
- „“.(falsche Identität!)

Um Interpretationsfehler zu vermeiden, können für und konkrete Zahlen eingesetzt und in der Prinzipskizze die entsprechende Anzahl der Quadrate visualisiert werden. Dargestellt ist das Beispiel
Auch die Grafik zeigt als Ergebnis:
Quadrate mit Seitenlänge gleich
Es wurde also das gemischte Glied, hier fortgelassen. Ein schrittweiser Analyseprozess des Fehlers wird von Hans-Georg Weigand, Alexander Schüler-Meyer und Guido Pinkernell wie folgt vorgeschlagen:[130]
1. Schritt: Bestimmen und erkennen des Fehlermusters
- „“.(falsche Identität!)
2. Schritt: Aufstellen einer Hypothese über die Fehlerursache: Die Ursache des Fehlers liegt vielleicht darin, dass eine grundlegende Struktur nicht wiedererkannt wird. Dies kann passieren, weil Schüler diese elementare Struktur nicht kennen oder weil der Term „zu komplex“ ist, um die Struktur wiederzuerkennen.
3. Schritt: Bearbeitung der Fehlerursache:
(a) Semantisch: Förderung der geometrischen Interpretation der Umformung zur Identifikation einer einfachen Struktur.
(b) Syntaktisch: Wiederholen der korrekten Struktur (semantisch entweder als Flächeninhalt eines Quadrats und/oder syntaktisch als die erste binomische Formel) sowie Üben des Wiedererkennens dieser Struktur im gegebenen Term.
4. Schritt: ein produktives Üben an strukturähnlichen Termen.
Eine weitere häufige Fehlerquelle ist das Ziehen von Quadratwurzeln aus Summen.[131] Analog zu oben gilt nicht
- „“.(falsche Identität!)
In korrekter Form lautet die Formel
Dabei sorgen die Beträge dafür, dass die positive Quadratwurzel gezogen wird, also etwa und nicht
Fehler können auch vermieden werden, indem man Unbekannte durch konkrete Zahlen ersetzt und eine zuvor hergeleitete Identität auf die Probe stellt. Es gilt etwa
- aber
weshalb eine Identität zwischen den Termen und nicht richtig sein kann.
Verallgemeinerungen[Bearbeiten | Quelltext bearbeiten]
Grundsätzlich sind Verallgemeinerungen der binomischen Formel in verschiedene Richtungen möglich.
- Zum einen kann die Anzahl der Summanden erhöht werden, also usw.
- Zum anderen kann der Exponent vergrößert werden, also usw.
Letztlich ist auch eine Kombination aus beiden Verallgemeinerungsrichtungen möglich.
Der binomische Lehrsatz[Bearbeiten | Quelltext bearbeiten]

Binomische Formeln lassen sich auch für höhere Potenzen angeben, diese Verallgemeinerung ist der binomische Lehrsatz: Für alle gilt[133][Anm. 5]
Dabei bezeichnen die Binomialkoeffizienten,[134] die beispielsweise mittels des Pascalschen Dreiecks leicht zu bestimmen sind. Gelegentlich wird die durch den binomischen Lehrsatz gegebene Formel auch als „binomische Formel“ oder „allgemeine binomische Formel“ bezeichnet.[57][135] Ähnlich existiert die Bezeichnung „zweite binomische Formel“ für die Ausmultiplizierung des allgemeinen Terms [136]
Die erste und die zweite binomische Formel sind Spezialfälle des binomischen Lehrsatzes für
Für ergibt sich z. B.
-
Geometrische Darstellung der kubischen binomischen Formel Dargestellt ist das Beispiel
Eine Verallgemeinerung auf nicht notwendig natürliche Exponenten führt auf eine Potenzreihenentwicklung, die durch die binomische Reihe gegeben ist:[1]
Diese allgemeinere Formel wurde erstmals 1826 von Niels Henrik Abel bewiesen.[137]
Verallgemeinerung der dritten binomischen Formel[Bearbeiten | Quelltext bearbeiten]
Auch zur dritten binomischen Formel gibt es eine Verallgemeinerung, die die Faktorisierung von ermöglicht:
oder allgemein für höhere natürliche Potenzen[138]
Aus einem Ausdruck lässt sich immer der Faktor abspalten. Ist eine Primzahl, ist das Quotientenpolynom irreduzibel; weitere Zerlegungen sind nur noch über die komplexen Zahlen möglich.[139] Andernfalls lässt sich die Summe weiter zerlegen und ist ein Produkt von 3 oder mehr verschiedenen ungeraden Primzahlen, entstehen auch Polynome mit Koeffizienten ungleich 0, −1, +1. So entsteht bei der Zerlegung von ein Polynom, beginnend mit
Mit erhält man als Quotientenpolynome die sogenannten Kreisteilungspolynome.[140]
Bei geradem lässt sich stets und damit auch abspalten; bei der Division entsteht als Quotientenpolynom eine alternierende Summe:[141][138]
- für
Bei ungeradem lässt sich zumindest abspalten; bei der Division entsteht als Quotientenpolynom eine alternierende Summe:[138]
- für
Erweiterungen auf mehrgliedrige Ausdrücke[Bearbeiten | Quelltext bearbeiten]
Eine Verallgemeinerung der binomischen Formeln auf Potenzen von Polynomen, also von Summen mit mehr als zwei Gliedern, führt auf das Multinomialtheorem. Beispielsweise gilt für das Quadrat eines Trinoms
Allgemein gilt[138]
Im Spezialfall von Trinomen[142] sind die Koeffizienten in der Pascalschen Pyramide enthalten. So gilt[143]
Auch bei mehrgliedrigen Ausdrücken finden sich Anwendungen in der Zahlentheorie. Der Vier-Quadrate-Satz besagt, dass sich jede natürliche Zahl als Summe von vier Quadratzahlen darstellen lässt.[144] Beispiele sind
Da es unendlich viele natürliche Zahlen gibt, ist es nicht möglich, alle Möglichkeiten einzeln durchzuprobieren, weshalb ein mathematischer Beweis dieser Tatsache über allgemeingültige logische Schlussfolgerungen geführt werden muss. Es erwähnte Leonhard Euler im Jahre 1748 in einem Brief an Christian Goldbach die Identität
die zeigt, dass sich das Produkt von Zahlen, die sich in vier Quadrate zerlegen lassen, wieder in 4 Quadrate zerlegen lässt. Da jede natürliche Zahl als Produkt von Primzahlen dargestellt werden kann (und der Satz für klar ist), lässt sich das Problem damit auf Primzahlen reduzieren:[145]
usw. Da es nach dem Satz des Euklid unendlich viele Primzahlen gibt, ist jedoch auch hier ein Durchprobieren nicht möglich. Allerdings kann der Vier-Quadrate-Satz speziell für Primzahlen über ein geometrisches Verfahren gezeigt werden, das zusätzlich gewisse Eigenschaften der Primzahlen ausnutzt.[146] Leonhard Euler versuchte 40 Jahre lang vergeblich, den Satz zu zeigen, bis 1770 schließlich Joseph-Louis Lagrange ein Beweis gelang.[147]
Die Frage, ob Zerlegbarkeit in eine gewisse Anzahl an Quadraten von Produkten zweier Zahlen – wo dies möglich ist – auf das Ergebnis weitervererbt wird, ist ganz allgemein Gegenstand der Quadrate-Sätze. Etwa behandelte Carl Ferdinand Degen den Fall von acht Quadraten. Adolf Hurwitz konnte mit dem Beweis des Kompositionssatzes zeigen, dass dies nur für die Anzahlen möglich ist. Dies bedeutet, dass neben und den Identitäten von Brahmagupta, Euler und Degen keine weiteren Identitäten oberen Typs existieren können.[148]
Multinomialtheorem[Bearbeiten | Quelltext bearbeiten]
Das Multinomialtheorem ist eine sehr weitreichende verallgemeinerung der binomischen Formeln, da sowohl beliebig viele Summanden in den Klammern als auch beliebig hohe Potenzen gleichzeitig erlaubt sind. Naturgemäß ist das Ausmultiplizieren dieser Klammern mit einer gewissen Komplexität verbunden. Das Multinomialtheorem besagt, dass[149]
Die Koeffizienten dieses Polynomausdrucks sind die Multinomialkoeffizienten
Dabei steht für die Fakultät von Eine kürzere Formulierung erlaubt die Multiindexnotation mit Multiindex [150]
Dabei identifiziert man mit dem Vektor
Das Multinomialtheorem hat unter anderem Anwendung in der Kombinatorik.[151]
In allgemeinen Ringen[Bearbeiten | Quelltext bearbeiten]
Ein Ring ist eine Menge, innerhalb derer mit Addition, Subtraktion und Multiplikation geschlossen gerechnet werden kann, und in der das Assoziativgesetz und das Distributivgesetz gelten.[152] Beispiele für Ringe sind die ganzen Zahlen aber auch die rationalen Zahlen Es wird jedoch im Allgemeinen nicht gefordert, dass die Multiplikation in einem Ring kommutativ ist. So sind etwa Matrizenringe im Allgemeinen nicht kommutativ. Daher lauten die binomischen Formeln in allgemeinen Ringen etwas anders:
aber auch
Da im Allgemeinen gilt, kann dies nicht weiter vereinfacht werden. Ist der Ring hingegen kommutativ, gelten die Formeln in ihrer gewohnten Gestalt.
Eine besondere Situation stellt sich in kommutativen unitären Ringen mit Charakteristik 2 ein. Hier gilt und somit vereinfachen sich erste und zweite binomische Formel jeweils zu
da das gemischte Glied entfällt.[153]
Literatur[Bearbeiten | Quelltext bearbeiten]
Zur Mathematik[Bearbeiten | Quelltext bearbeiten]
- Herbert Amann, Joachim Escher: Analysis 1. 3. Auflage. Birkhäuser, Basel/Boston/Berlin 2006, ISBN 978-3-7643-7755-7.
- Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Springer Spektrum, Berlin/Heidelberg 2022, ISBN 978-3-662-64388-4.
- Hans-Jochen Bartsch: Taschenbuch Mathematischer Formeln. 19. Auflage. Fachbuchverlag Leipzig im Carl Hanser Verlag, München/Wien 2001, ISBN 3-446-21792-4.
- Edwin F. Beckenbach, Richard Bellmann: Inequalities. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 30, Second Revised Printing, Springer-Verlag, Berlin / Heidelberg / New York 1965.
- Albrecht Beutelspacher: Zahlen, Formeln, Gleichungen. Springer-Verlag, Wiesbaden 2018, ISBN 978-3-658-16105-7.
- David M. Bressoud: Factorization and Primality Testing. Springer Verlag, New York / Berlin / Heidelberg 1989, ISBN 0-387-97040-1.
- I. N. Bronstein, K. A. Semendjajew et al.: Taschenbuch der Mathematik. 6. Auflage. Verlag Harri Deutsch, Frankfurt am Main 2006, ISBN 978-3-8171-2006-2.
- John B. Conway: Functions of One Complex Variable I. 2. Auflage. Springer Verlag, New York 1978, ISBN 0-387-90328-3.
- Theodore W. Gamelin: Complex Analysis. Springer-Verlag, New York 2001, ISBN 978-0-387-95093-8.
- Stefan Hildebrandt: Analysis 1. Springer-Verlag, Berlin/Heidelberg 2006, ISBN 978-3-540-25368-6.
- Kenneth Ireland, Michael Rosen: A Classical Introduction to Modern Number Theory. Second Edition, Springer-Verlag, New York 1990, ISBN 0-387-97329-X.
- Richard Isaac: The Pleasures of Probability. Springer Verlag, New York 1995, ISBN 978-1-4612-6912-0.
- Jens Carsten Jantzen, Joachim Schwermer: Algebra. 2. Auflage, Springer Spektrum Berlin, Heidelberg 2014, ISBN 978-3-642-40532-7.
- Achim Klenke: Wahrscheinlichkeitstheorie (= Springer-Lehrbuch Masterclass.). 3., überarbeitete und ergänzte Auflage, Springer Spektrum, Berlin/Heidelberg 2013, ISBN 978-3-642-36018-3.
- Neal Koblitz: A Course in Number Theory and Cryptography. Second Edition, Springer-Verlag, New York 1994, ISBN 3-540-94293-9.
- Dirk Langemann, Vanessa Sommer: So einfach ist Mathematik. 2. Auflage, Springer-Verlag, Berlin 2018, ISBN 978-3-662-55822-5.
- Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Springer Verlag, Berlin 2022, ISBN 978-3-662-66286-1.
- Serge Lang: A First Course in Calculus. Fifth Edition, Springer-Verlag, New York 1986, ISBN 0-387-96201-8.
- Pavle Mladenovic: Combinatorics. Springer-Verlag, Switzerland 2019, ISBN 978-3-030-00830-7.
- Kristina Reiss, Gerald Schmieder: Basiswissen Zahlentheorie. 3. Auflage, Springer-Verlag, Berlin/Heidelberg 2014, ISBN 978-3-642-39772-1.
- Thomas Rießinger: Gleichungen, Umformungen, Terme. Springer-Verlag, Berlin/Heidelberg 2016, ISBN 978-3-662-49334-2.
- Joseph H. Silverman, John Tate: Rational points on elliptic curves. Springer-Verlag, New York 1992, ISBN 0-387-97825-9.
- I. N. Stewart, D. O. Tall: Algebraic Number Theory. Chapman and Hall, London 1979, ISBN 978-0-412-13840-9.
- Terence Tao: Analysis I. Third Edition, Hindustan Book Agency, New Delhi 2017, ISBN 978-93-80250-64-9.
- Gabor Toth: Elements of Mathematics. Springer Nature Switzerland AG, 2021, ISBN 978-3-030-75050-3.
- Guido Walz (Hrsg.): Lexikon der Mathematik. Band 1. 2. Auflage, Springer-Verlag, Heidelberg 2017, ISBN 978-3-662-53497-7.
- Guido Walz (Hrsg.): Lexikon der Mathematik. Band 4. 2. Auflage, Springer-Verlag, Mannheim 2017, ISBN 978-3-662-53499-1.
Didaktik und Schulbücher[Bearbeiten | Quelltext bearbeiten]
- Hans Borucki, et al.: Klett KomplettTrainer Mathematik 8. Klasse. PONS GmbH, Stuttgart 2021, ISBN 978-3-12-927582-5.
- Kirsten Heckmann, Friedhelm Padberg: Unterrichtsentwürfe Mathematik Sekundarstufe I. Springer-Verlag, Berlin/Heidelberg 2012, ISBN 978-3-8274-2933-9.
- Lisa Hefendehl-Hebeker, Sebastian Rezat: Algebra: Leitidee Symbol und Formalisierung. In: Regina Bruder, Andreas Büchter, Hedwig Gasteiger, Barbara Schmidt-Thieme, Hans-Georg Weigand: Handbuch der Mathematikdidaktik (123–158). Zweite Auflage, Springer-Verlag, Berlin 2023, ISBN 978-3-662-66603-6.
- Andreas Pallack (Hrsg.): Fundamente der Mathematik. Cornelsen, Sachsen-Anhalt, Gymnasium Klasse 8, Berlin 2016, ISBN 978-3-06-009197-3.
- Felicitas Pielsticker: Mathematische Wissensentwicklungsprozesse von Schülerinnen und Schülern. Springer-Verlag, Wiesbaden 2020, ISBN 978-3-658-29948-4.
- Günther Rolles, Michael Unger (Hrsg.): Duden Basiswissen Schule: Mathematik, 5. bis 10. Klasse. 7. Auflage, Bibliographisches Institut GmbH, Berlin 2021, ISBN 978-3-411-71045-4.
- Katrin Schiffer: Probleme beim Übergang von Arithmetik zu Algebra. Springer-Verlag, Wiesbaden 2019, ISBN 978-3-658-27776-5.
- Hans-Georg Weigand, Alexander Schüler-Meyer, Guido Pinkernell: Didaktik der Algebra. 4. Auflage, Springer-Verlag, Berlin 2022, ISBN 978-3-662-64659-5.
- Udo Wennekers (Hrsg.): Zahlen und Größen 8. Nordrhein-Westfalen. Cornelsen, Berlin 2015, ISBN 978-3-06-002886-3.
Zur Geschichte[Bearbeiten | Quelltext bearbeiten]
- Die Elemente von Euklid. In: Ostwalds Klassiker der exakten Wissenschaften. Band 235, Verlag Europa-Lehrmittel, 4. Auflage, 2015, ISBN 978-3-8085-5482-1.
- H.-W. Alten, A. Djafari Naini, B. Eick, M. Folkerts, H. Schlosser, K.-H. Schlote, H. Wesemüller-Kock, H. Wußing: 4000 Jahre Algebra. 2. Auflage, Springer-Verlag, Berlin/Heidelberg 2014, ISBN 978-3-642-38238-3.
- J. L. Berggren: Episodes in the Mathematics of Medieval Islam. 2. Auflage. Springer-Verlag, New York 2016, ISBN 978-1-4939-3778-3.
- Carl B. Boyer: A History of Mathematics. Second Edition, John Wiley & Sons, 1991, ISBN 0-471-54397-7.
- Franka Miriam Brückler: Geschichte der Mathematik kompakt. Springer-Verlag, Berlin 2017, ISBN 978-3-662-55351-0.
- Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Springer-Verlag, Berlin/Heidelberg 2011, ISBN 978-3-642-13766-2.
- Dietmar Herrmann: Die antike Mathematik. 2. Auflage, Springer-Verlag, Berlin 2020, ISBN 978-3-662-61394-8.
- Victor J. Katz: A History of Mathematics – An Introduction. 3. Auflage. Addison-Wesley/Pearson, Boston 2009, ISBN 978-0-321-38700-4.
- Franz Lemmermeyer: 4000 Jahre Zahlentheorie. Springer-Verlag, Berlin 2023, ISBN 978-3-662-68109-1.
- Peter Schreiber, Sonja Brentjes: Euklid. BSB B. G. Teubner Verlagsgesellschaft, Leipzig 1987, ISBN 978-3-322-00377-5.
- John Stillwell: Mathematics and Its History. Third Edition, Springer-Verlag, New York / Dordrecht / Heidelberg / London 2010, ISBN 978-1-4419-6052-8.
- Heinz Klaus Strick: Mathematik – einfach genial! Springer-Verlag, Deutschland 2020, ISBN 978-3-662-60448-9.
Populärwissenschaftlich[Bearbeiten | Quelltext bearbeiten]
- Albrecht Beutelspacher: Albrecht Beutelspachers Kleines Mathematikum. Die 101 wichtigsten Fragen und Antworten zur Mathematik. C. H. Beck, München 2011, ISBN 978-3-406-61658-7, Kapitel 50: Wozu sind die binomischen Formeln gut?
- Heinrich Zankl: Irrwitziges aus der Wissenschaft. 1. Auflage, neue Ausgabe. Wiley, Weinheim 2012, ISBN 978-3-527-64142-0.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Binomische Formeln Rechner – Online Rechner mit Variablen. In: schule-verstehen.de (mit Rechenweg und Variablen).
- Binomische Formeln – Multiple Choice Test. In: mathe-online.at.
- Binomische Formeln. In: Serlo.
- Binomische Formel hoch 3. In: nachhilfe-team.net.
Anmerkungen[Bearbeiten | Quelltext bearbeiten]
- ↑ Die einzigen Ausnahmen betreffen die Fälle, in denen mindestens ein Summand gleich Null ist.
- ↑ Es hat die andere Lösung hier keine sinnvolle Interpretation.
- ↑ Für eine Unterscheidung ist für deren Betonung die Darstellung geeigneter, was jedoch äquivalent zur ersten binomischen Formel ist.
- ↑ Im Gegensatz zum Faktorisieren ist es extrem schnell möglich, Quadratwurzeln aus selbst sehr großen Zahlen zu ziehen.
- ↑ Es bezeichnet das Summenzeichen.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ a b c d e Guido Walz (Hrsg.): Lexikon der Mathematik. Band 1. Heidelberg 2017, S. 224.
- ↑ Dirk Langemann, Vanessa Sommer: So einfach ist Mathematik. Berlin 2018, S. 31.
- ↑ Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 66.
- ↑ Andreas Pallack (Hrsg.): Fundamente der Mathematik. Berlin 2016, S. 22.
- ↑ Albrecht Beutelspacher: Albrecht Beutelspachers Kleines Mathematikum. Die 101 wichtigsten Fragen und Antworten zur Mathematik. München 2011, S. 96.
- ↑ Heinrich Zankl: Irrwitziges aus der Wissenschaft. Weinheim 2012, Kapitel Klangvolle Namen (eingeschränkte Vorschau in der Google-Buchsuche)
- ↑ Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 70.
- ↑ Vergleiche Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 20–22.
- ↑ Dirk Langemann, Vanessa Sommer: So einfach ist Mathematik. Berlin 2018, S. 29–33.
- ↑ Felicitas Pielsticker: Mathematische Wissensentwicklungsprozesse von Schülerinnen und Schülern. Wiesbaden 2020, S. 116–128.
- ↑ Andreas Pallack (Hrsg.): Fundamente der Mathematik. Berlin 2016, S. 24–25.
- ↑ a b Willy Bennewitz, Fritz Warnecke, Günther Dross: Lehr- und Übungsbuch der Mathematik für Ingenieur- und Fachschulen. Band 1, Frankfurt am Main / Zürich 1963, S. 34.
- ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 30.
- ↑ Willy Bennewitz, Fritz Warnecke, Günther Dross: Lehr- und Übungsbuch der Mathematik für Ingenieur- und Fachschulen. Band 1, Frankfurt am Main / Zürich 1963, S. 35.
- ↑ Felicitas Pielsticker: Mathematische Wissensentwicklungsprozesse von Schülerinnen und Schülern. Wiesbaden 2020, S. 132.
- ↑ H.-W. Alten, A. Djafari Naini, B. Eick, M. Folkerts, H. Schlosser, K.-H. Schlote, H. Wesemüller-Kock, H. Wußing: 4000 Jahre Algebra. Berlin/Heidelberg 2014, S. 43.
- ↑ H.-W. Alten, A. Djafari Naini, B. Eick, M. Folkerts, H. Schlosser, K.-H. Schlote, H. Wesemüller-Kock, H. Wußing: 4000 Jahre Algebra. Berlin/Heidelberg 2014, S. 35–36.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 22–23.
- ↑ Franz Lemmermeyer: 4000 Jahre Zahlentheorie. Berlin 2023, S. 93.
- ↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt. Berlin 2017, S. 60–61.
- ↑ a b Euclid’s Elements of Geometry. In: Euclidis Elementa. Edidit et Latine interpretatus est I.L. Heiberg, in aedibus B.G. Teubneri, 1883–1885, Übersetzung von Richard Fitzpatrick, S. 52–54.
- ↑ Rudolf Haller (Übersetzer): Euklid: Elemente Stoicheia, Buch II, Proposition 4. (PDF; 209 KB) Markgröningen: Edition Opera-Platonis, 2010, abgerufen am 5. März 2024.
- ↑ Lisa Hefendehl-Hebeker, Sebastian Rezat: Algebra: Leitidee Symbol und Formalisierung. In: R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme, H.-G. Weigang: Handbuch der Mathematikdidaktik (123–158), Berlin 2015, S. 125.
- ↑ Rudolf Haller (Übersetzer): Euklid: Elemente Stoicheia, Buch II, Proposition 5. (PDF; 209 KB) Markgröningen: Edition Opera-Platonis, 2010, abgerufen am 5. März 2024.
- ↑ Peter Schreiber, Sonja Brentjes: Euklid. Leipzig 1987, S. 49–50.
- ↑ Peter Schreiber, Sonja Brentjes: Euklid. Leipzig 1987, S. 50.
- ↑ Sabetai Unguru: On the need to rewrite the history of Greek mathematics. In: Archive for History of Exact Sciences. Band 15, Nr. 1, 1975, S. 67–114, doi:10.1007/bf00327233, JSTOR:41133441.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 4.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. V–VI.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. VI.
- ↑ B. L. van der Waerden: Defence of a “Shocking” point of view. In: Archive for History of Exact Sciences. Band 15, Nr. 3, 1976, S. 199–210, doi:10.1007/bf00412256.
- ↑ André Weil: Who betrayed Euclid? (Extract from a letter to the editor). In: Archive for History of Exact Sciences. Band 19, Nr. 2, 1978, S. 189–200, JSTOR:41133469.
- ↑ Hans Freudenthal: What is algebra and what has been its history? In: Archive for History of Exact Sciences. Band 16, Nr. 3, 1976, S. 189–200, JSTOR:230723.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 55.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 51.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 52.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 39–43.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 41.
- ↑ Kristina Reiss, Gerald Schmieder: Basiswissen Zahlentheorie. Berlin/Heidelberg 2014, S. 30–31.
- ↑ Zur Vorgehensweise des Boethius siehe Paola Paolucci: Boezio traduttore di Nicomaco nel De institutione arithmetica. In: Athenaeum. (Pavia) 93, 2005, S. 227–241.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 347.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 383.
- ↑ Franz Lemmermeyer: 4000 Jahre Zahlentheorie. Berlin 2023, S. 131.
- ↑ Franz Lemmermeyer: 4000 Jahre Zahlentheorie. Berlin 2023, S. 131.
- ↑ Albrecht Beutelspacher: Zahlen, Formeln, Gleichungen. Wiesbaden 2018, S. 323.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 384.
- ↑ Franz Lemmermeyer: 4000 Jahre Zahlentheorie. Berlin 2023, S. 132.
- ↑ Ambros Sturm: Geschichte der Mathematik, G. J. Göschen'sche Verlagshandlung, Leipzig 1911, S. 49–50.
- ↑ Victor J. Katz: A History of Mathematics – An Introduction. Boston 2009, S. 285–287.
- ↑ J. L. Berggren: Episodes in the Mathematics of Medieval Islam. New York 2016, S. 140–143.
- ↑ Heinz Klaus Strick: Mathematik – einfach genial! Deutschland 2020, S. 109.
- ↑ Evelyn Kennedy: Omar Khayyam. The Mathematics Teacher. LIX (3), 1966: 140–142. doi:10.5951/MT.59.2.0140. JSTOR 27957296.
- ↑ a b Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 19.
- ↑ Günther Rolles, Michael Unger (Hrsg.): Duden Basiswissen Schule: Mathematik, 5. bis 10. Klasse. 7. Auflage, Berlin 2021, S. 128.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 20.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 21.
- ↑ a b Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 79.
- ↑ Vergleiche Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 141.
- ↑ Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 76.
- ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 83.
- ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 84.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. 427–435.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 22.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 180.
- ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 85–90.
- ↑ Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 160.
- ↑ Vergleiche Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 95–98.
- ↑ Hans-Georg Weigand, Alexander Schüler-Meyer, Guido Pinkernell: Didaktik der Algebra. Berlin 2022, S. 279–280.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 18–19.
- ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 36–37.
- ↑ Kirsten Heckmann, Friedhelm Padberg: Unterrichtsentwürfe Mathematik Sekundarstufe I. Berlin/Heidelberg 2012, S. 250.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 81.
- ↑ Vergleiche Richard Isaac: The Pleasures of Probability. New York 1995, S. 61–63.
- ↑ Vergleiche Achim Klenke: Wahrscheinlichkeitstheorie. Berlin/Heidelberg 2013, S. 12.
- ↑ Richard Isaac: The Pleasures of Probability. New York 1995, S. 63–64.
- ↑ Achim Klenke: Wahrscheinlichkeitstheorie. Berlin/Heidelberg 2013, S. 102–106.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 89–90.
- ↑ Terence Tao: Analysis I. New Delhi 2017, S. 253.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. 62.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. 59–61.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. 62–65.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. 76–77.
- ↑ Stefan Hildebrandt: Analysis 1. Berlin/Heidelberg 2006, S. 186.
- ↑ Neal Koblitz: A Course in Number Theory and Cryptography. New York 1994, S. 92.
- ↑ Neal Koblitz: A Course in Number Theory and Cryptography. New York 1994, S. 92–94.
- ↑ Neal Koblitz: A Course in Number Theory and Cryptography. New York 1994, S. 94–96.
- ↑ David M. Bressoud: Factorization and Primality Testing. New York 1989, S. 58–60.
- ↑ Neal Koblitz: A Course in Number Theory and Cryptography. New York 1994, S. 143–144.
- ↑ Neal Koblitz: A Course in Number Theory and Cryptography. New York 1994, S. 94.
- ↑ Franz Lemmermeyer: Mathematik à la Carte – Babylonische Algebra. Berlin 2022, S. 92.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 76.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. 9–10.
- ↑ Edwin F. Beckenbach, Richard Bellmann: Inequalities. Berlin / Heidelberg / New York 1965, S. 2.
- ↑ Edwin F. Beckenbach, Richard Bellmann: Inequalities. Berlin / Heidelberg / New York 1965, S. 4.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 143.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 142.
- ↑ Vergleiche Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 145.
- ↑ Tilo Arens, Frank Hettich, Christian Karpfinger, Ulrich Kockelhorn, Klaus Lichtenegger, Hellmuth Stachel: Mathematik. 5. Auflage, Berlin/Heidelberg 2022, S. 128.
- ↑ Vergleiche Theodore W. Gamelin: Complex Analysis. New York 2001, S. 8.
- ↑ John B. Conway: Functions of One Complex Variable I. New York 1978, S. 6.
- ↑ Theodore W. Gamelin: Complex Analysis. New York 2001, S. 11.
- ↑ Theodore W. Gamelin: Complex Analysis. New York 2001, S. 7.
- ↑ Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 10–12.
- ↑ Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 13.
- ↑ Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 13–14, 33.
- ↑ Gabor Toth: Elements of Mathematics. Switzerland 2021, S. 274, 285–286.
- ↑ Joseph H. Silverman, John Tate: Rational points on elliptic curves. New York 1992, S. 13.
- ↑ Franz Lemmermeyer: 4000 Jahre Zahlentheorie. Berlin 2023, S. 27–28.
- ↑ Dietmar Herrmann: Die antike Mathematik. Berlin 2020, S. 58.
- ↑ Kristina Reiss, Gerald Schmieder: Basiswissen Zahlentheorie. Berlin/Heidelberg 2014, S. 188.
- ↑ Franka Miriam Brückler: Geschichte der Mathematik kompakt. Berlin 2017, S. 142.
- ↑ Kenneth Ireland, Michael Rosen: A Classical Introduction to Modern Number Theory. New York 1990, S. 278–279.
- ↑ Hans-Georg Weigand, Alexander Schüler-Meyer, Guido Pinkernell: Didaktik der Algebra. Berlin 2022, S. 2.
- ↑ Hans-Georg Weigand, Alexander Schüler-Meyer, Guido Pinkernell: Didaktik der Algebra. Berlin 2022, S. 4.
- ↑ Udo Wennekers (Hrsg.): Zahlen und Größen 8. Nordrhein-Westfalen. Berlin 2015, S. 12–34.
- ↑ Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 69.
- ↑ Andreas Pallack (Hrsg.): Fundamente der Mathematik. Berlin 2016, S. 21 ff.
- ↑ Lisa Hefendehl-Hebeker, Sebastian Rezat: Algebra: Leitidee Symbol und Formalisierung. In: R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme, H.-G. Weigang: Handbuch der Mathematikdidaktik (123–158), Berlin 2015, S. 123–124.
- ↑ Katrin Schiffer: Probleme beim Übergang von Arithmetik zu Algebra. Wiesbaden 2019, S. 123.
- ↑ Felicitas Pielsticker: Mathematische Wissensentwicklungsprozesse von Schülerinnen und Schülern. Wiesbaden 2020, S. 96.
- ↑ Serge Lang: A First Course in Calculus. New York 1986, S. x.
- ↑ Hans Borucki, et al.: Klett KomplettTrainer Mathematik 8. Klasse. Stuttgart 2021, S. 18–22.
- ↑ Vergleiche Andreas Pallack (Hrsg.): Fundamente der Mathematik. Berlin 2016, S. 22 ff.
- ↑ Für mehr Details zu den Lehrplänen im Fach Mathematik in den einzelnen Bundesländern, siehe auch: Bildungsserver: Lehrpläne der einzelnen Bundesländer. Abgerufen am 10. März 2024.
- ↑ Lambacher Schweizer 7/8 Schulbuch: Grundlagen der Mathematik für Schweizer Maturitätsschulen. Lambacher Schweizer, 2011, ISBN 978-3-264-83981-4 Kapitel I 1–2.
- ↑ Mathias Bortenschlager et al.: Lösungswege 3. Österreichischer Bundesverlag Schulbuch GmbH & Co. KG, Wien 2023, ISBN 978-3-209-11127-2, S. 102–106.
- ↑ Günther Rolles, Michael Unger (Hrsg.): Duden Basiswissen Schule: Mathematik, 5. bis 10. Klasse. 7. Auflage, Berlin 2021, S. 256–257.
- ↑ Günther Rolles, Michael Unger (Hrsg.): Duden Basiswissen Schule: Mathematik, 5. bis 10. Klasse. 7. Auflage, Berlin 2021, S. 149 ff.
- ↑ Dirk Langemann, Vanessa Sommer: So einfach ist Mathematik. Berlin 2018, S. 82.
- ↑ Hans-Georg Weigand, Alexander Schüler-Meyer, Guido Pinkernell: Didaktik der Algebra. Berlin 2022, S. 109.
- ↑ Thomas Rießinger: Gleichungen, Umformungen, Terme. Berlin/Heidelberg 2016, S. 130.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 48.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 70.
- ↑ Guido Walz (Hrgb.): Lexikon der Mathematik. Band 1. 2. Auflage, Heidelberg 2017, S. 223–224.
- ↑ Dirk Langemann, Vanessa Sommer: So einfach ist Mathematik. Berlin 2018, S. 158.
- ↑ I. N. Bronstein, K. A. Semendjajew et al.: Taschenbuch der Mathematik. Frankfurt am Main 2006, S. 12–13.
- ↑ Ernst Hairer, Gerhard Wanner: Analysis in historischer Entwicklung. Berlin/Heidelberg 2011, S. 274.
- ↑ a b c d I. N. Bronstein, K. A. Semendjajew et al.: Taschenbuch der Mathematik. Frankfurt am Main 2006, S. 12.
- ↑ Jens Carsten Jantzen, Joachim Schwermer: Algebra. Heidelberg 2014, S. 158–159.
- ↑ Jens Carsten Jantzen, Joachim Schwermer: Algebra. Heidelberg 2014, S. 158.
- ↑ Hans-Jochen Bartsch: Taschenbuch Mathematischer Formeln. München/Wien 2001, S. 60.
- ↑ Günther Rolles, Michael Unger (Hrsg.): Duden Basiswissen Schule: Mathematik, 5. bis 10. Klasse. 7. Auflage, Berlin 2021, S. 126.
- ↑ Heinz Klaus Strick: Mathematik – einfach genial! Deutschland 2020, S. 257.
- ↑ I. N. Stewart, D. O. Tall: Algebraic Number Theory. London 1979, S. 149.
- ↑ John Stillwell: Mathematics and Its History. New York / Dordrecht / Heidelberg / London 2010, S. 423.
- ↑ I. N. Stewart, D. O. Tall: Algebraic Number Theory. London 1979, S. 149–150.
- ↑ I. N. Stewart, D. O. Tall: Algebraic Number Theory. London 1979, S. 150.
- ↑ Guido Walz (Hrsg.): Lexikon der Mathematik. Band 4. 2. Auflage, Mannheim 2017, S. 297.
- ↑ Pavle Mladenovic: Combinatorics. Switzerland 2019, S. 42.
- ↑ Herbert Amann, Joachim Escher: Analysis 1. Basel/Boston/Berlin 2006, S. 71.
- ↑ Pavle Mladenovic: Combinatorics. Switzerland 2019, S. 42–48.
- ↑ Jens Carsten Jantzen, Joachim Schwermer: Algebra. Heidelberg 2014, S. 81.
- ↑ Jens Carsten Jantzen, Joachim Schwermer: Algebra. Heidelberg 2014, S. 86.





































































![Veranschaulichung der dritten binomischen Formel über einen Perspektivwechsel: Die blaue Fläche wird geflippt, um zum zweiten Bild zu gelangen.[15]](http://upload.wikimedia.org/wikipedia/commons/thumb/5/5b/Binom3_color.svg/778px-Binom3_color.svg.png)





























































































































































![Wahrscheinlichkeiten sind Konzepte der Maßtheorie und können damit als „Teilvolumina“ des „Ganzen mit Volumen Eins“ gesehen werden.[74] Sie messen Plausibilität. Um Zahl-Zahl zu werfen, muss „die Hälfte einer Hälfte“ getroffen werden, also ein Viertel. Analog: Triff an jeder Seite des Quadrats die „richtige Hälfte“ (für Zahl-Zahl hier „rechts“ und „unten“), was dann zur gezeigten Aufteilung in Flächen führt, und in diesem Fall alle vier Möglichkeiten gleich plausibel macht.](http://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/01_Wahrscheinlichkeits-Quadrat_2_M%C3%BCnzenw%C3%BCrfe.svg/450px-01_Wahrscheinlichkeits-Quadrat_2_M%C3%BCnzenw%C3%BCrfe.svg.png)
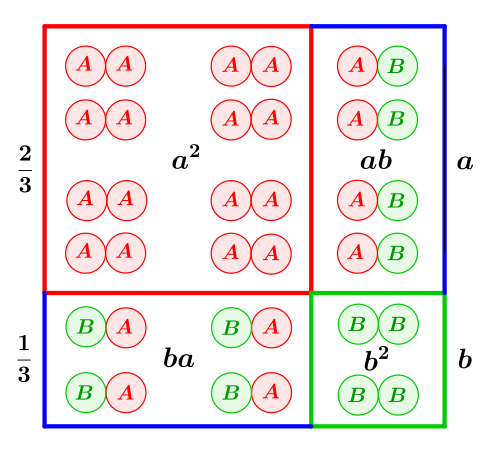





![{\displaystyle \mathrm {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e855c523912e0552431adc64db30321c734b1ca2)
![{\displaystyle X-\mathrm {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e089ce07aaa8dbd4b7faa65d59a1a151cfd5b13e)
![{\displaystyle {\begin{aligned}\operatorname {Var} (X)&=\operatorname {E} \left[(X-\operatorname {E} [X])^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}-2X\operatorname {E} [X]+\operatorname {E} [X]^{2}\right]\\[4pt]&=\operatorname {E} \left[X^{2}\right]-2\operatorname {E} [X]\operatorname {E} [X]+\operatorname {E} [X]^{2}\\[4pt]&=\operatorname {E} \left[X^{2}\right]-\operatorname {E} [X]^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89e8f56e83f6aac0448dcb72fdb6fc16a75fded1)


![{\displaystyle \operatorname {E} \left[XY\right]^{2}\leq \operatorname {E} \left[X^{2}\right]\operatorname {E} \left[Y^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a69ac27d223459479f19876e40fd4dcf757fd6)
![{\displaystyle \operatorname {E} \left[X\right]^{2}\leq \operatorname {E} \left[X^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51504e1009fa026931e9fab28cb140049e70e5a4)




































































































































































































































