Volumengrafik

Die Volumengrafik ist ein Fachgebiet der 3D-Computergrafik. In der Volumengrafik werden Objekte durch Voxelgitter modelliert.
Bedeutung[Bearbeiten | Quelltext bearbeiten]
Die Volumengrafik ist in der Lage, transparente Objekte – z. B. lichtdurchlässiges Hautgewebe – und Objekte ohne scharfe Abgrenzungen – wie z. B. Wolken – zu modellieren und mit hoher Genauigkeit und Wirklichkeitstreue bildlich darzustellen. Sie ist für bildgebende Verfahren von großer Bedeutung, da diese von Natur aus Voxeldaten erzeugen, ansonsten ist sie nur wenig verbreitet. Das rührt daher, dass bislang keine gerätebasierte Beschleunigung existiert, wie sie mit Grafikprozessoren für die Oberflächengrafik gang und gäbe ist.
Physikalische Grundlage[Bearbeiten | Quelltext bearbeiten]
Die Volumengrafik basiert auf dem Strahlungstransport, der beschreibt, wie sich Licht auf dem Weg durch ein Volumen verhält und dessen Quintessenz die Strahlungstransportgleichung ist. Sie verknüpft die Strahldichte mit dem Absorptionskoeffizienten, dem Streukoeffizienten und der Emissionsleistung des zu passierenden Materials. Dabei hängen die Absorptionskoeffizienten und Streukoeffizienten, sowie die Emissionsleistung u. a. von der Dichte und der Temperatur des Materials ab. In der folgenden Gleichung wird der Streukoeffizient mit , die Emissionsleistung mit , die Strahldichte als spezifische Intensität und der Richtungsvektor der Lichtstrahlen mit bezeichnet.
Da die Berechnung der Strahlungstransportgleichung einen zu hohen Rechenaufwand erfordert, trifft die Volumengrafik zunächst drei Vereinfachungen:
- Voxel werden nur direkt von Lichtquellen beleuchtet. Indirekte Beleuchtung durch Streuung und Reflexion von anderen Voxeln wird nicht berücksichtigt.
- Es gibt nur direkte Lichtquellen, keine fluoreszierenden oder selbst leuchtenden Objekte innerhalb der Szene.
- Die Beleuchtung wird durch ein einfaches Beleuchtungsmodell beschrieben. Bewährt hat sich das Phong-Beleuchtungsmodell.
Mit der Streuung können nun auch die Vektoren der Gleichung ignoriert werden. Anschaulich folgt man dadurch nur noch einem Lichtstrahl, der niemals die Richtung ändert. Dadurch lässt sich die Strahlungstransportgleichung in die einfachere Visualisierungsgleichung überführen:
Diese Differentialgleichung lässt sich analytisch lösen. Es folgt die Diskretisierung dieser Lösung und die Abschätzung einiger kleinerer Terme. Das Ergebnis ist die folgende zum Rendern benutzte rekursive Formel:[1]
die meist in der Kurzschreibweise mit dem over-Operator angegeben wird:
Bildverarbeitung[Bearbeiten | Quelltext bearbeiten]
Jedes Bildverarbeitungsprogramm erlaubt in der Regel das Laden und Speichern einer ganzen Reihe von Dateiformaten. Damit wird dem Anwender die Möglichkeit gegeben, abhängig von seinen weiteren Plänen das für ihn sinnvollste Format zu verwenden. Er kann ein Grafikformat danach wählen, ob Speicherplatz gespart werden soll, ob das Bild mehr oder weniger schnell aufgebaut werden muss usw.
Dateiformate, die sich für den Umgang mit dreidimensionalen Daten eignen, speichern Beschreibungen von Form und Farbe künstlich erzeugter 3D-Modelle und Objekten der realen Welt. Modelle der dreidimensionalen Objektrepräsentation bestehen häufig aus Polygonen und glatten Oberflächen, die ihrerseits mit Beschreibungen bestimmter Eigenschaften wie Farbe, Texturen, Reflexionen etc. kombiniert werden. Dazu gehören zum Beispiel die Dateiformate DXF, Wavefront OBJ, 3DS, VRML und X3D.
Zunehmend an Bedeutung gewinnen daneben Ansätze der Volumengrafik, bei denen Objekte in kleine Voxel zerlegt werden und jedem Voxel Eigenschaften wie Farbe oder Transparenz zugeordnet werden.
Rendern[Bearbeiten | Quelltext bearbeiten]
Schritte[Bearbeiten | Quelltext bearbeiten]
Beim Rendern von Volumengrafiken unterscheidet man vier Schritte:
-
Klassifikation.
-
Interpolation.
-
Shading
-
Compositing.
Die Reihenfolge dieser Schritte ist nicht zwingend vorgegeben, generell gelten nur die beiden Regeln: Die Klassifikation muss vor dem Shading stattfinden und das Compositing kommt zuletzt.
Klassifikation[Bearbeiten | Quelltext bearbeiten]
Bei der Klassifikation werden den Voxeln Materialeigenschaften zugewiesen. Bei der Erzeugung eines Voxels wird nur ein einziger Wert abgelesen, bei der Computertomografie beispielsweise die Röntgendichte, bei der Magnetresonanztomografie der Gehalt an Protonen oder Wasserstoffatomkernen. Dieser Wert liefert nicht genug Informationen über das Material, etwa welche Farbe es hat oder ob es stark spiegelnd ist. Bei der Klassifikation wird daher nach Benutzervorgaben aus dem einzelnen Wert eine ganze Reihe von Werten gemacht. Steht beispielsweise der hohe Wert eines Voxels für einen hohen Wassergehalt, so könnte man daraus folgern, dass es sich um weiches Körpergewebe handelt, das wiederum leicht rosafarben, etwas durchsichtig und überhaupt nicht spiegelnd ist. Üblicherweise wird das Material über das Phong-Beleuchtungsmodell charakterisiert.
Shading[Bearbeiten | Quelltext bearbeiten]
Beim Shading wird bestimmt, wie viel Licht von einem Voxel aus in Richtung des Betrachters reflektiert wird und welche Farbe es hat. Üblicherweise wird dazu das Phong Shading verwendet. Um das Phong-Shading in seiner Ursprungsdefinition verwenden zu können, würde jeder Voxel eine Normale benötigen. Die Normale ist ein Vektor, der in der Oberflächengrafik senkrecht von der betrachteten Oberfläche weg deutet. Da in der Volumengrafik aber keine Oberflächen vorliegen, muss hier ein anderer Weg beschritten werden. Statt der Normalen wird daher in jedem Voxel der Gradient verwendet. Der Gradient zeigt stets in Richtung der stärksten Materialänderung und kommt damit den physikalischen Gedanken, dass Licht nur am Übergang zwischen verschiedenen Materialschichten reflektiert wird, am nächsten.
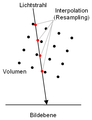
Interpolation[Bearbeiten | Quelltext bearbeiten]
Bei der Interpolation, auch Resampling genannt, werden die Materialeigenschaften an Punkten zwischen den Voxeln aus den umgebenden Voxeln angenähert. Voxel sind Punkte und damit nulldimensionale Objekte, das heißt, sie besitzen weder Länge noch Breite noch Höhe. Dadurch ist es äußerst unwahrscheinlich, dass ein durch das Volumen verlaufender Sichtstrahl auch nur ein einziges Voxel trifft. Das Interpolationsverfahren legt fest, wie man aus den Voxeln Informationen über den zwischen ihnen liegenden Raum gewinnt. In der Volumengrafik ist die lineare Interpolation vorherrschend. Zwischen zwei Voxeln wird linear, zwischen vier Voxeln, die ein Rechteck bilden, bilinear und zwischen acht Voxeln, die einen Quader bilden, trilinear interpoliert.
Compositing[Bearbeiten | Quelltext bearbeiten]
Beim Compositing werden die von in einer Reihe liegenden Voxeln gelieferten Lichtbeiträge miteinander verrechnet, um einen endgültigen Bildpunkt zu erhalten. Das Compositing setzt die eigentliche Summation der Visualisierungsgleichung um: Licht durchquert ein Voxel und ändert dabei Intensität und Farbe, dann durchquert es den nächsten Voxel und ändert wiederum Intensität und Farbe. Diese Reihe wird fortgesetzt, bis das Licht auf die Bildebene fällt und dort ein Pixel einfärbt.
Techniken[Bearbeiten | Quelltext bearbeiten]

Im Laufe der Zeit wurden vier Techniken entwickelt, um Voxeldaten zu rendern:
- Volume Raycasting. Analog zum Raytracing werden hier Sehstrahlen in das Volumen hineingeworfen. Nachdem die Interaktion des Lichts mit dem Volumen berechnet ist, werden die Beiträge entlang des Sehstrahls aufsummiert und ergeben so ein Pixel im Bild.
- Splatting. Die Voxel werden nacheinander auf die Bildfläche geworfen, wo sie zu einem Splat zerplatzen und ihren Farbbeitrag auf mehrere nebeneinander liegende Pixel des Bildes verteilen.
- Shear-Warp. Das Voxelgitter selbst wird geschert und entsprechend der Perspektive verzerrt, anschließend wird für jedes Pixel ein Sehstrahl in das Volumen geschickt. Durch die Scherung und die Verzerrung des Gitters läuft der Sehstrahl innerhalb des Volumens parallel zu den Achsen und kann dadurch sehr einfach berechnet werden.
- 3D Texture Mapping. Statt eine Volumenrenderingtechnik zu verwenden, erzeugt man hier ein Primitiv und weist diesem die Voxeldaten als 3D-Textur zu. Die Visualisierung des Volumens erfolgt dann über die Texturierung im Rahmen der normalen Oberflächengrafik.
Man unterscheidet bildbasierte und objektbasierte Techniken, je nachdem, ob die Berechnung vom Bild oder vom Volumen ausgeht, sowie Mischformen der beiden. Volume Raycasting ist ein bildbasiertes Verfahren, Splatting ein objektbasiertes, Shear-Warp und 3D Texture Mapping sind Mischformen.[2]
Erweiterungen[Bearbeiten | Quelltext bearbeiten]

Schattenwurf in Voxelgrafiken ist keine triviale Aufgabe. Die bei Oberflächengrafiken verwendeten Techniken Schattenvolumen und Z-Puffer-Schattierung sind hier nicht anwendbar, da sie undurchsichtige Flächen voraussetzen. Bis heute gibt es nur zwei Verfahren, die einigermaßen einfach sind:
Grants Technik berechnet einen Schattenwurf unter Verwendung einer einzelnen Lichtquelle, die aus einem Winkel von 45° relativ zur Blickrichtung des Betrachters paralleles Licht in die Szene wirft, also unendlich weit entfernt ist. Zunächst wird ein Z-Buffer für die vorderste senkrechte Scheibe des Volumens eingerichtet, der überall mit dem Wert 1 initialisiert wird. Für diese Schicht wird nun das Shading berechnet, indem für jedes Voxel die Abstrahlung in Richtung Betrachter als (Lichtstärke des einfallenden Lichts) * (Wert im Z-Buffer) berechnet wird. Nun wird der Z-Buffer einen Voxel seitlich von der Lichtquelle weg und nach hinten verschoben. Von jedem Wert im Z-Buffer wird die Absorption durch den in Richtung Lichtquelle direkt davor liegenden Voxel abgezogen. Es folgt die Abstrahlberechnung, gefolgt von einer weiteren Verschiebung usw.
Meinzers Technik arbeitet ähnlich wie Grants Technik, verwendet aber eine zusätzliche Lichtquelle hinter dem Betrachter selbst, die in einer Ebene mit der schräg ausgerichteten Lichtquelle liegt. Dadurch lässt sich der benötigte Z-Buffer auf eine Voxelreihe verkleinern. Durch die zusätzliche Lichtquelle wird der Schatten aufgehellt.
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Torsten Möller, Universität Wien: Direct Volume Rendering
- ↑ VIS, Universität Stuttgart: Direct Volume Rendering