Leitungstheorie
Die Leitungstheorie ist ein Teilgebiet der Elektrotechnik. Sie befasst sich mit Erscheinungen auf elektrischen Leitungen, deren Länge in der Größenordnung der Wellenlänge des übertragenen Signalspektrums oder darüber liegt, und findet hauptsächlich Anwendung in der Fernmeldetechnik, der Hochfrequenztechnik, der Impulstechnik und in der elektrischen Energieversorgung bei Hochspannungsleitungen.
Die Leitungstheorie benutzt das Modell der elektrischen Doppelleitung und beschreibt diese durch das Ersatzschaltbild eines „unendlich kurzen“ Leitungsstückes, dessen Elemente von den Leitungsbelägen bestimmt werden. Ohne das elektromagnetische Feld mit Hilfe der Maxwellschen Gleichungen selbst zu ermitteln, leitet sie daraus ein System partieller Differentialgleichungen (die sogenannten Leitungsgleichungen) ab und versucht diese mit verschiedenen, den jeweiligen Randbedingungen angepassten, mathematischen Methoden zu lösen.
Dadurch gelingt es, die Vorgänge und Wellenphänomene (z. B. Reflexionen, stehende Wellen, negatives Überschwingen, Widerstandstransformationen), die im Zusammenhang mit Leitungen auftreten, qualitativ zu verstehen, quantitativ zu fassen und für die praktischen Anwendungen richtig zu interpretieren. Schließlich entstehen Regeln für den Einsatz der Leitung als Bauelement in der Elektrotechnik, speziell in der Nachrichtentechnik und der Elektronik.
Hintergrund[Bearbeiten | Quelltext bearbeiten]
Nur für Gleichstrom oder Wechselstrom niedriger Frequenz lässt sich eine Leitung grob mit dem ohmschen Widerstand aus Leitungsquerschnittsfläche, Leitfähigkeit und Länge beschreiben. Sobald die Wellenlänge der Signale in der Größenordnung der Leitungslänge liegt oder schnelle Schaltvorgänge auf Leitungen beschrieben werden sollen, reicht dieses stark vereinfachte Modell nicht aus. Durch die auf jeder Leitung vorhandenen Kapazitäts- und Induktivitätsbeläge breiten sich die Signale maximal mit Lichtgeschwindigkeit aus. Wenn die räumliche Ausdehnung eines elektrischen Systems so groß ist, dass die Laufzeit der zu verarbeitenden Signale nicht mehr vernachlässigt werden kann, treten neben dem „normalen“ Verhalten besondere Wellenphänomene auf. Die Beschreibung solcher Systeme erfordert mathematische Verfahren, die den Ort der Signale in die Betrachtungen einbeziehen.
Beispielsweise besitzt eine Wechselspannung von 1 GHz im Vakuum eine Wellenlänge von etwa 30 cm. Wellenvorgänge spielen deshalb auf den Platinen moderner Computer eine große Rolle. Aufgrund der hochfrequenten Taktung werden die Daten durch sehr kurze Impulse mit steilen Flanken dargestellt und übertragen. Deshalb wären solche Systeme ohne Anwendung der Erkenntnisse der Leitungstheorie nicht realisierbar.
Für die Methoden der klassischen Leitungstheorie dürfen allerdings der technische Leiterabstand nicht größer als die halbe Wellenlänge der entstehenden Wellen und der Widerstandsbelag nicht zu groß sein, so dass nur die transversalen elektromagnetischen Felder (TEM-Wellen) eine Rolle spielen. Nur dann kann man ein „unendlich kurzes“ Leitungsstück durch ein Ersatzschaltbild aus konzentrierten Bauelementen beschreiben. Ist das nicht der Fall, so müssen die Maxwellschen Gleichungen direkt gelöst werden. Damit beschäftigen sich die Hoch- und Höchstfrequenztechnik in den Theorien der Hohlraumwellen und der Antennensysteme.
Geschichte[Bearbeiten | Quelltext bearbeiten]
Die 1850 begonnene Verlegung von transatlantischen Seekabeln und die bei derartig langen Kabeln auftretenden starken Verzerrungen erforderten eine theoretische Analyse der Vorgänge auf „langen Leitungen“. Als erster beschäftigte sich um 1855 William Thomson mit der Beschreibung der Vorgänge auf Leitungen. 1886 formulierte Oliver Heaviside diese Erkenntnisse in ihrer heutigen Form als Leitungsgleichung und begründete damit die allgemeine Leitungstheorie. Er fand die nach ihm benannte Heaviside-Bedingung, aus der zu erkennen war, dass die Probleme der Verzerrung wesentlich durch die hohen Leitungskapazitäten verursacht wurden. Rudolf Franke betrachtete die Leitung 1891 erstmals mit den Mitteln der Vierpoltheorie. Zur Lösung des Verzerrungsproblems schlug 1900 Mihajlo Pupin die Bespulung von Leitungen zur künstlichen Erhöhung ihrer Induktivität vor. Damit stand auch der Realisierung von langen Fernsprechleitungen nichts mehr im Weg. Um 1903 betrachtete George Ashley Campbell die Leitung als Kettenleiter. Mit dem Aufkommen der Hochfrequenztechnik am Anfang des 20. Jahrhunderts war es notwendig, schon kurze Leitungen mit den Mitteln der Leitungstheorie zu behandeln. Sie konnten dabei als verlustlos betrachtet und außer zur Signalübertragung auch als Bauelement (z. B. zur Widerstandstransformation) eingesetzt werden. Alle diese Anwendungen beruhten bis dahin auf sinusförmigen Signalen und konnten deshalb mit Hilfe der komplexen Wechselstromrechnung gelöst werden. Mitte des 20. Jahrhunderts erforderte die Impulstechnik und später die Digitaltechnik die unverfälschte Übertragung von kurzen Impulsen über Leitungen. Dazu war es erforderlich, die Analyse mit Hilfe einer Operatorenrechnung, graphisch mit einem Impulsfahrplan oder (falls speicherfreie Bauelemente mit nichtlinearen Kennlinien angeschlossen werden) mit dem Bergeron-Verfahren durchzuführen. Zur Analyse der Impulsausbreitung auf verlustbehafteten Leitungen wurden numerische Verfahren entwickelt.
Die Leitungsgleichungen[Bearbeiten | Quelltext bearbeiten]
Die Leitungsgleichungen einer homogenen linearen Zweidrahtleitung lassen sich aus dem in folgender Abbildung gezeigten Ersatzschaltbild eines solchen Leitungsabschnitts der infinitesimalen Länge dx bestimmen:
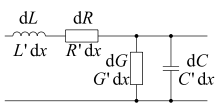
Die darin enthaltenen Größen sind die mit der Länge dx multiplizierten Leitungsbeläge: Der Induktivitätsbelag L′, der Kapazitätsbelag C′, der Widerstandsbelag R′ und der Ableitungsbelag G′.
Aus Spannung u(x,t) und Strom i(x,t) am Anfang, aus Spannung u(x+dx,t) und Strom i(x+dx,t) am Ende dieses Elements der Leitung ergeben sich unter Zuhilfenahme von Maschensatz und Knotenpunktsatz die beiden partiellen Differentialgleichungen der homogenen Leitung (die ausführliche Herleitung erfolgt im Artikel Leitungsgleichung):
Dabei sind Spannung u und Strom i jeweils nach unten bzw. nach rechts (in +x-Richtung) eingeführt. Die Hauptaufgabe der Leitungstheorie ist die Lösung dieses DGL-Systems für die Anfangs- und Randbedingungen der verschiedensten praktischen technischen Anwendungen und damit die Ermittlung des Verlaufs von Spannung u(x,t) und Strom i(x,t) auf der Leitung in Abhängigkeit vom Ort x und der Zeit t.
Sonderfall: Sinusförmige Signale[Bearbeiten | Quelltext bearbeiten]
In vielen Fällen der Wechselstromtechnik und der klassischen Nachrichtentechnik reicht es praktisch aus, die Spannung und den Strom sowohl als rein sinusförmig (harmonisch) als auch Einschalt- und Einschwingvorgang als abgeschlossen zu betrachten. Dann treten auch auf einer Leitung nur (stationäre) sinusförmige Signale auf. In diesem besonderen Fall kann die komplexe Wechselstromrechnung angewendet werden und weil die Zeitabhängigkeit entfällt, reduzieren sich die Leitungsgleichungen auf ein System gewöhnlicher Differentialgleichungen für die auf der Leitung vorhandenen vom Ort x abhängigen komplexen Amplituden U(x) und I(x):
Sie werden in der Literatur oft als „komplexe Leitungsgleichungen“ bezeichnet. Bei linearer Beschaltung der beiden Leitungsenden kann in diesem Fall eine geschlossene Lösung der Leitungsgleichungen angegeben werden.
Sonderfall: Verlustlose Leitungen[Bearbeiten | Quelltext bearbeiten]
Bei kurzen und/oder bei Hochfrequenzleitungen kann man praktisch die Verluste durch Widerstands- und Ableitungsbelag vernachlässigen. Dadurch vereinfachen sich die Leitungsgleichungen wie folgt:
Wenn man dieses DGL-System zu einer einzigen partiellen Differentialgleichung umformt, dann erhält man die klassische eindimensionale Wellengleichung.
Weil dann auf der Leitung weder Dämpfung noch Verzerrung auftreten (die Heaviside-Bedingung ist „automatisch“ erfüllt), lassen sich die Gleichungen in vielen Fällen einfach lösen und die erhaltenen Lösungen lassen sich besonders anschaulich deuten. Die Ergebnisse dieser Idealisierung stellen trotzdem das wesentliche Verhalten einer Leitung richtig dar und sind außerdem für den „Einstieg in die Leitungstheorie“ von didaktischer Bedeutung.
Sonderfall: Sinusförmige Signale auf der verlustlosen Leitung[Bearbeiten | Quelltext bearbeiten]
Durch die Kombination dieser beiden Sonderfälle erhält man die folgende besonders einfache Form der „komplexen Leitungsgleichungen“:
Da ihre hauptsächliche Bedeutung in der Hochfrequenztechnik liegt, sind sie der Ausgangspunkt für die Theorie der Hochfrequenzleitungen, dem „didaktischen Paradebeispiel“ der Leitungstheorie.
Die allgemeine Lösung der Leitungsgleichungen[Bearbeiten | Quelltext bearbeiten]
Der erste Schritt der Leitungstheorie zur Lösung der Leitungsgleichungen ist die Ermittlung der allgemeinen Lösung des DGL-Systems. Diese besitzt frei wählbare (Integrations-)Konstanten oder Funktionen, welche anschließend durch Festlegung der an den konkreten Anwendungsfall angepassten Anfangs- und Randbedingungen noch festgelegt werden müssen. Da das DGL-System der Leitungsgleichungen linear ist, kann die allgemeine Lösung im allgemeinen Fall beispielsweise mit Hilfe der Laplace-Transformation ermittelt werden.
Bei der Ermittlung der allgemeinen Lösung stößt man auf wesentliche Kenngrößen der Leitung, wie die Phasen- und Gruppengeschwindigkeit bzw. die Ausbreitungskonstante (Fortpflanzungskonstante) sowie den Wellenwiderstand (Wellenimpedanz). Im Allgemeinen sind die letzten beiden Größen komplizierte Operatoren im Sinne der Operatorenrechnung. Insbesondere die Ausbreitungskonstante ist verantwortlich für die Ausbreitung der Wellen auf der Leitung, ihre Geschwindigkeit, ihre Dämpfung und ihre Verformung.
In folgenden Sonderfällen ist die allgemeine Lösung allerdings relativ leicht ermittelbar.
Sonderfall: Verlustlose Leitungen[Bearbeiten | Quelltext bearbeiten]
Mit den Definitionen für den (reellen) Wellenwiderstand der verlustlosen Leitung
und die (konstante) Phasengeschwindigkeit der verlustlosen Leitung
erhält man die allgemeine (sogenannte d'Alembertsche) Lösung
Dabei sind uh(t) und ur(t) zwei Zeitfunktionen, die noch durch die Randbedingungen festgelegt werden müssen. Der Nachweis der Richtigkeit kann durch Einsetzen in die „verlustlosen“ Leitungsgleichungen erbracht werden.
Diese allgemeine Lösung kann wie folgt interpretiert werden:
- Der linke Term der Lösung stellt eine vom Anfang zum Ende der Leitung hinlaufende (beliebig geformte) Welle dar.
- Der rechte Term stellt eine vom Ende zum Anfang der Leitung zurücklaufende Welle dar.
- Beide Wellen haben die Geschwindigkeit v0.
- Sie werden auf der Leitung weder gedämpft noch in ihrer Form verzerrt.
- Der Wellenwiderstand Z0 stellt das Verhältnis von Spannung und Strom der jeweiligen Welle dar.
Sonderfall: Sinusförmige Signale[Bearbeiten | Quelltext bearbeiten]
Mit den Definitionen für den komplexen Wellenwiderstand (Wellenimpedanz)
und die komplexe Ausbreitungskonstante (Fortpflanzungskonstante)
erhält man entsprechend den Lösungsverfahren (z. B. Exponentialansatz) für lineare Differentialgleichungen die allgemeine Lösung
Dabei sind Uh0 und Ur0 die beiden noch unbestimmten komplexen Integrationskonstanten, welche durch die Randbedingungen festgelegt werden müssen. Der Nachweis der Richtigkeit kann durch Einsetzen in die „komplexen Leitungsgleichungen“ erbracht werden.
Diese allgemeine Lösung kann wie folgt interpretiert werden:
- Der linke Term der Lösung stellt eine vom Anfang zum Ende der Leitung hinlaufende sinusförmige Welle (Wanderwelle) dar.
- Der rechte Term stellt eine vom Ende zum Anfang der Leitung zurücklaufende sinusförmige Welle dar.
- Diese Wellen werden aufgrund der (im Allgemeinen frequenzabhängigen) Dämpfungskonstante α gedämpft und entsprechend der (immer) frequenzabhängigen Phasenkonstante β in der Phase gedreht. Wegen der im Allgemeinen nichtlinearen Frequenzabhängigkeit der Phasenkonstante muss man zwischen Phasengeschwindigkeit und Gruppengeschwindigkeit unterscheiden.
- Der komplexe Wellenwiderstand ZLtg stellt jeweils das Verhältnis der komplexen Amplituden von Spannung und Strom der jeweiligen Welle dar. Demgegenüber ist durch die Interferenz von hin- und rücklaufender Welle das Verhältnis von Gesamtspannung U(x) zu Gesamtstrom I(x) nicht konstant, es entstehen stehende Wellen, die durch ihr Stehwellenverhältnis charakterisiert werden.
Sonderfall: Verzerrungsfreie Leitung[Bearbeiten | Quelltext bearbeiten]
Schon Oliver Heaviside hat gezeigt, dass auf einer Leitung, deren Leitungsbeläge die nach ihm benannte Heaviside-Bedingung
erfüllen, die „über die Leitung laufenden Wellen“ in ihrer Form (trotz Dämpfung) nicht verzerrt werden. Das bedeutet gleichzeitig, dass die Phasengeschwindigkeit nicht von der Frequenz abhängt und deshalb keine Dispersion auftritt, also benachbarte Frequenzgruppen nicht „auseinander laufen“. Diese wünschenswerte Eigenschaft wird aber normalerweise von einer realen Leitung aufgrund des überwiegenden Kapazitätsbelages nicht erfüllt. Um trotzdem möglichst lange verzerrungsfreie Fernsprechleitungen zu realisieren, hat man praktisch den Induktivitätsbelag künstlich erhöht (Bespulte Leitung, Krarupkabel).
Das Betriebsverhalten einer Leitung[Bearbeiten | Quelltext bearbeiten]
Im zweiten Schritt ermittelt die Leitungstheorie aus der allgemeinen Lösung eine konkrete (partikuläre) Lösung, indem die verbleibenden Freiheitsgrade durch Festlegung von Rand- und Anfangsbedingungen eliminiert werden.
- Wird einerseits eine Leitung zur Signalübertragung verwendet, dann ist an ihrem Anfang ein aktiver (Generator-)Zweipol angeschlossen und an ihrem Ende ein passiver Lastzweipol. Wenn eine über die Leitung laufende Welle auf das Ende oder den Anfang der Leitung trifft, dann kann sie dort reflektiert werden. Dabei wird sie im Allgemeinen in ihrer Größe und in ihrer Form (falls sie nicht sinusförmig ist) geändert. Die Impedanz des jeweiligen Abschlusses und der Wellenwiderstand bestimmen dabei, wie das passiert. Zur quantitativen Beschreibung der Reflexionen dienen die Reflexionsfaktoren am Anfang und am Ende der Leitung.
- Anderseits ist es möglich, die Leitung als Vierpol zu betrachten und aus der allgemeinen Lösung die Vierpolparameter zu bestimmen.
Unter folgenden speziellen Randbedingungen hat die Leitungstheorie Methoden entwickelt, um geschlossene partikuläre Lösungen zu ermitteln:
- Enthalten sowohl der Generator- als auch der Lastzweipol einer verlustlosen Leitung nur lineare ohmsche Widerstände, dann gibt es eine geschlossene Lösung als (durch auftretende Mehrfachreflexionen) unendliche Reihe. Die Ausbreitung einer einzelnen Impulsflanke kann grafisch als Impulsfahrplan (engl.: Lattice Diagram) dargestellt und berechnet werden.
- Enthalten der Generator- und/oder der Lastzweipol einer verlustlosen Leitung nichtlineare speicherfreie Widerstände, dann kann die Ausbreitung einer einzelnen Impulsflanke grafisch mit Hilfe des Bergeron-Verfahrens ermittelt werden.
- Enthalten sowohl der Generator- als auch der Lastzweipol beliebige lineare Bauelemente, dann ist die Lösung mit Hilfe der Laplace-Transformation (oder einer anderen Operatorenrechnung) zu ermitteln. Ist die Leitung verlustlos, dann ist das manuell machbar, ist sie dagegen verlustbehaftet, dann sind im Allgemeinen rechentechnische/numerische Verfahren notwendig.
- Enthalten sowohl der Generator- als auch der Lastzweipol einer verlustbehafteten Leitung beliebige lineare Bauelemente und ist die Generatorspannung (rein) sinusförmig, dann ist die Lösung mit Hilfe der komplexen Wechselstromrechnung geschlossen zu ermitteln.
Sonderfall: Unendlich lange Leitung[Bearbeiten | Quelltext bearbeiten]
In diesem Fall gibt es nur eine hinlaufende Welle (den linken Term der allgemeinen Lösung). Das Verhältnis von Spannung zu Strom auf jeder Stelle der Leitung entspricht dem Wellenwiderstand. Daraus folgt eine wichtige „Deutung“ des Wellenwiderstandes: Der Eingangswiderstand einer unendlich langen Leitung ist gleich ihrem Wellenwiderstand. Der Generatorzweipol wirkt also wie ein Spannungsteiler aus seinem Innenwiderstand und dem Wellenwiderstand.
Dieser theoretische Fall wird in der Praxis dann annähernd erreicht, wenn die Leitung sehr lang und dadurch ihre Dämpfung so groß ist, dass die am Ende reflektierte Welle praktisch am Leitungsanfang „nicht mehr messbar“ ist.
Sonderfall: Mit dem Wellenwiderstand ausgangsseitig abgeschlossene Leitung[Bearbeiten | Quelltext bearbeiten]
Wird eine endlich lange Leitung mit einem passiven Zweipol abgeschlossen, dessen Impedanz gleich dem Wellenwiderstand der Leitung ist, dann wirkt das genauso, als würde sich die Leitung ins Unendliche fortsetzen. Deshalb verhält sich eine mit dem Wellenwiderstand abgeschlossene (angepasste) Leitung genau wie eine unendlich lange Leitung, insbesondere gibt es nur eine hinlaufende Welle und ihr Eingangswiderstand ist ebenfalls gleich dem Wellenwiderstand.
Sonderfall: Mit dem Wellenwiderstand eingangsseitig abgeschlossene Leitung[Bearbeiten | Quelltext bearbeiten]
In diesem Fall bewegt sich ein (gegenüber der Verzögerungszeit der Leitung) kurzer Impuls als „Wellenzug“ vom Eingang zum Ausgang und wird dort teilweise oder total reflektiert. Dabei wird er im Allgemeinen verformt und läuft zum Eingang zurück, wo keine weitere Reflexion auftritt und seine Energie im Generatorinnenwiderstand „verbraucht“ wird. Trotz eingangsseitiger Anpassung können im Fall stationärer sinusförmiger Signale durch die Interferenz von vor- und zurücklaufender Welle stehende Wellen auftreten.
Beispiel: Sinusförmige Signale auf der verlustlosen Leitung[Bearbeiten | Quelltext bearbeiten]
Für das „Paradebeispiel“ der Leitungstheorie, die praktisch wichtige Hochfrequenzleitung, sollen hier die vollständigen Lösungen angegeben werden. Die allgemeine Lösung vereinfacht sich in diesem Fall zu
wobei die Ausbreitungskonstante aufgrund fehlender Dämpfung nur noch durch die linear von der Frequenz abhängige Phasenkonstante repräsentiert wird:
Dabei ist λ die Wellenlänge auf der Leitung, welche um den Verkürzungsfaktor geringer ist als die Wellenlänge einer elektromagnetischen Welle gleicher Frequenz im Vakuum.
Betriebsverhalten einer beidseitig abgeschlossenen Leitung[Bearbeiten | Quelltext bearbeiten]
Besitzen an einer Leitung der Länge L der Generatorzweipol eine innere (komplexe) Impedanz ZG und eine Leerlaufspannung UG sowie der Lastzweipol eine innere (komplexe) Impedanz Z2, dann erhält man aus der allgemeinen Lösung nach der Ermittlung der beiden Konstanten Uh0 und Ur0 die endgültige Lösung als Überlagerung einer hinlaufenden und einer rücklaufenden Welle
Während der Herleitung dieser Lösung werden der komplexe Reflexionsfaktor am Ausgang definiert als
und der komplexe Reflexionsfaktor am Eingang als
Damit können die Signale auf der Leitung an jeder Stelle x für jede konkrete lineare Beschaltung des Aus- und Eingangs ermittelt werden. Es zeigt sich, dass das Verhältnis von hin- und rücklaufender Welle allein von der Beschaltung am Ausgang abhängt und dass es vorteilhaft ist, den verallgemeinerten (komplexen) Reflexionsfaktor für eine beliebige Stelle x der Leitung wie folgt zu definieren:
In der Praxis interessiert oft der leicht messbare Verlauf der Amplitude bzw. des Effektivwertes der meist vorhandenen stehenden Wellen. Er ergibt sich relativ zur hinlaufenden Welle am Ausgang zu
Wenn man Maximal- und Minimalwert der stehenden Welle in Beziehung setzt, erhält man daraus als wichtiges Maß für die Fehlanpassung das Stehwellenverhältnis (SWR):
Die Hochfrequenzleitung als Vierpol[Bearbeiten | Quelltext bearbeiten]
Gibt man als Randbedingungen zur Ermittlung einer partikulären Lösung alternativ Spannung U2 und Strom I2 am Ende der Leitung vor, dann erhält man für die Spannung U(x) und den Strom I(x) auf der Leitung:
Für x = 0 errechnet man die Spannung U1 und den Strom I1 am Anfang der Leitung und erhält damit die Vierpol-Ketten-Gleichungen der Leitung:
Sie sind die Basis zur Nutzung eines Leitungsstückes als hochfrequenztechnisches Bauelement.
Leitungstransformation[Bearbeiten | Quelltext bearbeiten]
Die Leitungstransformation oder auch Impedanztransformation bezeichnet die Eigenschaft, die Impedanz am Anfang einer Leitung, als Z1 bezeichnet, durch die Länge LLtg und den Leitungswellenwiderstand ZLtg und durch den Abschluss der Leitung mit der Impedanz Z2 verändern zu können. Dabei wird eine näherungsweise verlustlose Leitung angenommen, bei der der Zusammenhang gilt:
mit der Wellenzahl und der Wellenlänge in der Beziehung:
Der Leitungswellenwiderstand ZLtg wird in diesem Zusammenhang auch als charakteristische Impedanz der Leitung bezeichnet – er ist unabhängig vom Abschluss und Länge der Leitung und ist durch die Leitungsbeläge bestimmt. Weiters ist die Wellenlänge in diesem Zusammenhang entlang einer Übertragungsleitung unterschiedlich zu der Wellenlänge bei Ausbreitung einer elektromagnetischen Welle im freien Raum. Dieser Zusammenhang wird durch den Verkürzungsfaktor beschrieben.
Ausgehend von dieser für die Leitungstransformation fundamentalen Beziehung analysiert die Leitungstheorie das Transformationsverhalten der Leitung bei bestimmten Leitungslängen wie den wichtigen Spezialfällen einer λ/4-Leitung oder λ/2-Leitung und bei bestimmten Leitungsabschlüssen wie Anpassung, Kurzschluss, Leerlauf, reeller Abschluss, Blindwiderstand als Abschluss und allgemeiner komplexer Abschluss.

Alternativ lassen sich Leitungstransformationen auch mithilfe des Smith-Diagrammes durchführen: Man dreht dazu den normierten Abschlusswiderstand im Smith-Diagramm lediglich im Winkel
um den Punkt (Leitungslänge , Generatorfrequenz , relative Dielektrizitätszahl , Vakuum-Lichtgeschwindigkeit ). Die normierte Eingangsimpedanz lässt sich dann direkt aus dem Smith-Diagramm ablesen.
Kurzgeschlossene Leitung[Bearbeiten | Quelltext bearbeiten]
Für eine am Ende kurzgeschlossene Leitung (Z2 = 0) vereinfacht sich die Gleichung zu
Das Verhältnis LLtg/λ = m bestimmt auf Grund der Vorzeichenregeln der Tangensfunktion, ob sich diese U-förmige Leitung wie eine Kapazität, eine Induktivität oder ein Schwingkreis verhält:
- Für 1/4 > m > 0 ist es eine Induktivität
- Für 1/4 = m ist es ein Parallelschwingkreis mit den Resonanzwellenlängen λ; λ/3; λ/5; …
- Für 1/2 > m > 1/4 ist es eine Kapazität.
- Für 1/2 = m ist es ein Reihenschwingkreis mit den Resonanzwellenlängen λ; λ/2; λ/4; …
Dieses Verhalten setzt sich für ungeradzahlige Vielfache periodisch fort.
Anmerkung: LLtg ist die tatsächliche geometrische Leitungslänge. Der Einfluss des Verkürzungsfaktors ist in der Wellenlänge enthalten.
In einigen speziellen Funkgeräten für sehr hohe Frequenzen wird bei Stichleitungen bzw. Lecher-Leitungen ein verschiebbarer Kurzschlussbügel verwendet, um die gewünschte Eigenschaft einstellen zu können. Im Regelfall wird keine symmetrische Doppelleitung verwendet, die Energie abstrahlt und deshalb nur einen geringen Gütefaktor besitzt, sondern ein geschlossener, zylindersymmetrischer Topfkreis.
Offene Leitung[Bearbeiten | Quelltext bearbeiten]
Für eine am Ende offene Leitung (Z2 → ∞) vereinfacht sich die Gleichung zu
Das Verhältnis LLtg/λ = m bestimmt, ob sich die leerlaufende Leitung wie eine Kapazität, eine Induktivität oder ein Schwingkreis verhält:
- Für 1/4 > m > 0 ist es eine Kapazität
- Für 1/4 = m ist es ein Reihenschwingkreis mit den Resonanzwellenlängen λ; λ/2; λ/4; …
- Für 1/2 > m > 1/4 ist es eine Induktivität.
- Für 1/2 = m ist es ein Parallelschwingkreis mit den Resonanzwellenlängen λ; λ/3; λ/5; …
Dieses Verhalten setzt sich für ungeradzahlige Vielfache periodisch fort.
λ/4-Leitung[Bearbeiten | Quelltext bearbeiten]

Für die Leitungslänge λ/4 vereinfacht sich die Gleichung zu der Transformationsbeziehung mit der Impedanz am Anfang einer Leitung zu:
Wird die λ/4-lange Leitung am Ende kurzgeschlossen (Z2 → 0), wirkt diese am Eingang wie ein Leerlauf, ist also hochohmig mit Z1 → ∞. Umgekehrt wirkt eine am Ende offene λ/4-lange Leitung am Eingang wie ein Kurzschluss. Der Leitungswellenwiderstand ZLtg spielt in beiden Fällen keine Rolle.
Die λ/4-Transformation setzt sich periodisch für ungeradzahlige Vielfache fort.
Anwendungsbeispiele[Bearbeiten | Quelltext bearbeiten]


Im oberen Bild wird eine Methode gezeigt, wie eine Hochfrequenz-Doppelleitung gestützt und geerdet werden kann, obwohl sie auf der Sollwellenlänge λ isoliert. Der Innenleiter einer luftgefüllten Koaxialleitung für hohe Übertragungsleistungen lässt sich auf vergleichbare Weise durch einen λ/4-Topfkreis stützen.
Entfernt man den unteren Querbügel, wirkt der λ/4-lange Stub wie ein selektiver Kurzschluss für ganz bestimmte Frequenzen, während er bei Gleichstrom isoliert. Damit kann die unerwünschte Ausbreitung von HF-Energie definierter Frequenz unterbunden werden.
Manche Bauelemente der Radartechnik wie Branch-Duplexer und Ringkoppler basieren auf der Impedanztransformation von λ/4-Leitungen.
In einen Hohlleiter wird die elektrische Energie mit einer Sonde (Stabantenne) eingekoppelt, die λ/4 vom geschlossenen Ende entfernt in den Hohlleiter hineinragt. Die sich von der Sonde des Kopplers ablösende elektromagnetische Welle „sieht“ an drei Seiten den unendlich hohen Widerstand der kurzgeschlossenen λ/4-Leitung, kann sich also nur in der verbleibenden Richtung ausbreiten.
Beim Mikrowellenherd ist die Resonanzdichtung (also die Türdichtung, die den Austritt von Mikrowellenenergie verhindert) ein umlaufendes Band aus einem λ/4-Kanal, der exakt 3 cm breit ist und dessen Metallflächen sich nicht berühren. Diese Breite passt zu der vom Magnetron erzeugten Wellenlänge 12 cm. Damit gelingt es auch ohne Verwendung störanfälliger Kontakte, das elektromagnetische Strahlungsfeld im Innenraum „einzusperren“.
Der Wilkinson-Teiler lässt sich am einfachsten als Leistungsaddierer erklären: Zwei Sender oder Antennen, jeweils mit der Quellimpedanz Z0 liefern gleichphasig Signale an die Tore P2 und P3. Die jeweils folgenden λ/4-Leitungen mit der Impedanz transformieren auf 2·Z0 am Tor P1, woraus sich durch Parallelschaltung wieder die Gesamtimpedanz Z0 ergibt. Der Widerstand 2·Z0 rechts zwischen P2 und P3 hat keine Auswirkung, solange die dort eintreffenden Signale gleichphasig sind. Die Energie gegenphasiger Signale wandelt er in Wärme um.
λ/2-Leitung[Bearbeiten | Quelltext bearbeiten]
Eine λ/2-lange Leitung transformiert nicht die Ausgangsimpedanz und es gilt für die Impedanz am Eingang unabhängig vom Leitungswellenwiderstand der λ/2-Leitung:
Wird eine λ/2-lange Leitung am Ende kurzgeschlossen (Z2 = 0), wirkt sie auch am Eingang wie ein Kurzschluss. Umgekehrt wirkt eine am Ende offene λ/2-lange Leitung auch am Eingang wie ein Leerlauf.
Anwendungsbeispiele[Bearbeiten | Quelltext bearbeiten]
In der Funktechnik verwendet man häufig Dipolantennen, deren Aufgabe darin besteht, die Impedanz des Senderausgangs auf den Wellenwiderstand des Vakuums (377 Ω) zu transformieren, damit die Energie effizient abgestrahlt werden kann.
Speist man einen nicht unterbrochenen λ/2-Dipol an einem Ende, misst man dort eine Impedanz Z1 ≈ 2200 Ω. Weil dieser Wert zu sehr von der Wellenimpedanz eines Koaxialkabels (Z ≈ 50 Ω) abweicht, würde ein unmittelbarer Anschluss zu einer untragbaren Fehlanpassung führen. Bei der eben beschriebenen Methode wurden – genau genommen – zwei λ/4-Stäbe elektrisch parallel betrieben, deshalb hat jeder der beiden die Impedanz Z1 ≈ 4400 Ω.
Um die Dipolimpedanz zu senken, wird der Dipol meist in der Mitte getrennt, denn dort misst man den erheblich geringeren Wert Z ≈ 70 Ω, der besser zur Kabelimpedanz passt. Dieses Messergebnis kann man auch als Reihenschaltung von zwei 35 Ω-Widerständen interpretieren – jeder λ/4-Stab hat die Impedanz Za = 35 Ω. Solche Groundplane-Antennen werden bei Mittelwellen-Rundfunksendern verwendet, an deren unterem Ende tatsächlich diese Impedanz Z2 = 35 Ω gemessen wird, wenn das obere Ende frei bleibt.
Setzt man diese Messwerte 4400 Ω und 35 Ω zu beiden Seiten eines λ/4-Stab in die Transformationsgleichung für die λ/4-Leitung ein:
erhält man ZLtg = 392 Ω, der dem Wert des Freiraumwellenwiderstandes Z0 nahekommt.
Weitere Teilgebiete der Leitungstheorie[Bearbeiten | Quelltext bearbeiten]
Um einige praktisch wichtige Probleme zu lösen, wird die klassische Leitungstheorie auf Basis der homogenen Doppelleitung mit konstanten Leitungsbelägen durch folgende Teilgebiete ergänzt:
- Einfluss des Skin-Effektes auf die Leitungsbeläge und die Wellenausbreitung
- Brechung durch Störstellen auf der Leitung oder an Koppelstellen von Leitungen
- Ersatzschaltungen für kurze Leitungen
- Leitungsschaltungen und Einsatz der Leitung als Bauelement
- Wellenausbreitung auf Mehrleitersystemen
- Gekoppelte Leitungen und Richtkoppler
- Übersprechen zwischen verschiedenen Leitungen
Leitungen in komplexen Strukturen[Bearbeiten | Quelltext bearbeiten]
Die Lösung der Leitungsgleichungen in Vierpolparameterform (z. B. als S-, Z- oder Y-Parameter) lässt sich für fortgeschrittene Betrachtungen als Matrix entweder zahlenmäßig oder formelmäßig in numerische bzw. symbolisch rechnende CAD-Systeme einspiegeln, die ihrerseits lineare Baugruppen mit n-Tor-Matrizen vernetzen. Auf der Basis der Kirchhoffschen Gesetze ergeben sich dann sofort die von Standard-CAD-Systemen bekannten, über 30 Ausgabegrößen der Hochfrequenzelektronik wie Spannungs- und Stromverstärkung, Eingangs- und Ausgangsimpedanz, verallgemeinerte Streuparameter, verschiedene Gewinnbegriffe etc., und zwar entweder als Zahlen oder als vollautomatisch hergeleitete Formelausdrücke. In der Praxis wird man insbesondere bei komplizierteren Strukturen aus vielen Leitungen und anderen linearen Baugruppen (R, L, C, Trafos, linearisierte Transistoren etc.) alle Formeln automatisch herleiten[1].
Übertragung der Leitungstheorie auf akustische Wellen und Wärmewellen[Bearbeiten | Quelltext bearbeiten]
Besonders angenehm ist, dass die gesamte elektrische Leitungstheorie mit der kompletten Begriffswelt der CAD-Systeme mit ganz einfachen Substitutionen auf viele andere Fragestellungen übertragbar ist[2], z. B. auf ebene akustische Wellen und ebene Wärmewellen, so dass derartige Probleme hervorragend mit den CAD-Systemen der Hochfrequenzelektronik analysierbar sind. Die Optimierungsalgorithmen und alle Bequemlichkeiten der Systeme stehen somit zur Verfügung. Da die Differentialgleichungen bis auf Substitutionen gleich sind, entsteht kein neues Problem.
Ebene akustische Wellen, die sich mit Druck px = U und Teilchengeschwindigkeit vx= I in x-Richtung ausbreiten, werden in der Leitungstheorie wegen der analogen Differentialgleichungen bei verlustlosem Stoff beschrieben durch R’=0, G’=0, L’ = ρ (Stoffdichte) und C’ als Elastizitätsmodul bzw. Kompressibilität (bei Gasen abhängig vom Adiabatenkoeffizient). Die Berechnung z. B. der Schallgeschwindigkeit v=1/(L’C’)1/2 fiele dabei als triviales Nebenergebnis ab. Eine immer noch sehr leicht zu lösende Aufgabe wäre die Frage nach der frequenzabhängigen Schalldämmung einer 3-fach verglasten Fensterscheibe. Man würde sie anhand der Kettenschaltung von 5 Leitungsvierpolen aus Glas-Luft-Glas-Luft-Glas berechnen, wobei als Generator- und Lastimpedanz jeweils der akustische Wellenwiderstand (L’/C’)1/2 von Luft zu nehmen wäre. Die Berechnung des Problems unterscheidet sich in nichts von den Schaltungsberechnungen in der Hochfrequenzelektronik. Der schwammige Begriff „Dämmung“ präzisiert sich dann zu dem aus der Elektronik wohlbekannten Standardbegriff „Gewinn“ G =|s21G|2 mit s21G als verallgemeinerter (generalized) Streuparameter, wie er in jedem CAD-System implementiert ist. Wäre bei f=1 kHz z. B. G = 1,5E-3, hätte man 28,2 dB Dämpfung (Dämmung).
Ebene Wärmewellen sind ebenfalls leicht mit dem Rüstzeug der Leitungstheorie analysierbar. Hier korrespondiert U mit der Temperatur und I mit dem Wärmestrom durch eine Fläche A. Es gilt G’=0 und L’=0. Die Größen R’ und C’ bestimmen sich aus Wärmeleitfähigkeit, spezifischer Wärme und Stoffdichte. Eine Wärmeleitung ist dabei eine stark dämpfende Leitung mit α=β. Da meist αL ≫1 ist, gibt es keine rücklaufende Welle, und die Eingangsimpedanz der Leitung ist gleich dem Wellenwiderstand (R’/jωC’)1/2. Temperatur und Wärmestrom (Spannung und Strom) sind dann bei x=0 um 45° gegeneinander phasenverschoben.
Elektrisch kurze Leitungen[Bearbeiten | Quelltext bearbeiten]


Eine für die Praxis wichtige Anwendung der Leitungstheorie sind die oben erwähnten Ersatzschaltungen für kurze Leitungen, für die sich die Lösungen der Leitungsgleichungen näherungsweise zum ohmschen Gesetz vereinfachen, falls Kapazitäts- und Ableitungsbelag der Leitungen vernachlässigbar sind.
Hierbei heißt eine Leitung der Länge elektrisch kurz[3], wenn sie kurz bezüglich der Wellenlänge der elektromagnetischen Welle auf der Leitung ist, d. h. falls . Daher wird für elektrisch kurze Leitungen die Annahme getroffen.
Bezeichnen und die komplexen Spannungen am Anfang und am Ende einer elektrisch kurzen Leitung der Länge , so gilt für die Leitung mit Impedanz näherungsweise
Anmerkung: Man beachte, dass die komplexen Stromstärken am Anfang und Ende der Leitung i. Allg. nicht übereinstimmen, d. h. . Sind Kapazitäts- und Ableitungsbelag jedoch vernachlässigbar, dann ist und mit näherungsweise das ohmsche Gesetz in der Form erfüllt (siehe Ersatzschaltbilder).
Herleitung: Die Beziehung ergibt sich, indem zunächst die partikuläre Lösung der Leitungsgleichungen für die Spannung im Sonderfall sinusförmiger Signale bei vorgegebener Spannung und vorgegebenen Strom am Ende der Leitung
unter Verwendung von und umgeformt wird zu
Nun verwendet man noch Folgendes:
- .
- Da die Leitung elektrisch kurz ist, darf man die Dämpfung () vernachlässigen, sodass .
- Wegen gilt und .
- Es gilt .
Setzt man dies in ein, so folgt wie gewünscht .
Andere Anwendungen der Leitungstheorie[Bearbeiten | Quelltext bearbeiten]
Generell ist bei allen Problemen, deren Differentialgleichungen formal auf die Struktur obiger Leitungsgleichungen zurückgeführt werden können, nach Feststellung der Analogiegrößen für U, I sowie R’, L’, G’ und C’ das Problem vollständig gelöst.
Zu dieser Klasse physikalischer Probleme gehören neben ebenen Wärmewellen und akustischen Wellen auch ebene elektromagnetische Wellen, die unter einem Winkel auf eine verlustfreie Schichtenfolge mit unterschiedlichen Werten für Permeabilität, Permittivität und Dicke L einfallen. Die Lösung der Maxwellschen Gleichungen eines Abschnitts lässt sich dann für die Komponenten des elektrischen und magnetischen Feldes noch in eine Vierpolform mit Wellenwiderstand und Ausbreitungsmaß umschreiben, die jeweils von den Materialwerten, Schichtdicken und Winkeln abhängen. Die verallgemeinerten Streuparameter s11G und s21G geben dann wie in der Hochfrequenzelektronik üblich mit |s21G|2 den transmittierten und mit |s11G|2 den reflektierten Leistungsbruchteil an.
Der idealste Verstärker ist stets ein Wanderwellenverstärker, bei dem eine Welle in eine Leitung reflexionsfrei hineinfliegt, mit negativem α verstärkt wird, dispersionsfrei wandert und am Ende reflexionsfrei in die Last transmittiert. In IC-Bauform realisiert man sie im Mikrowellenbereich näherungsweise als Leitung aus einigen Kettenleiterabschnitten jeweils aus Ls und Cs, wobei statt G’ ein FET genommen wird, der mit seiner Stromquelle für α < 0 und somit für eine Verstärkung der hinlaufenden Welle sorgt. Bei Lichtwellenleitern hat man das Analogon als erbiumdotierten Faserverstärker. Im Medizinbereich lassen sich Blutbahnen mit Leitungsgleichungen modellieren.
Grenzen der Leitungstheorie[Bearbeiten | Quelltext bearbeiten]
Die Leitungstheorie ist spätestens dann nicht mehr anwendbar, wenn die Wellen beginnen, sich im Zick-Zack auszubreiten, aber auch dann, wenn komplexere Strukturen zu analysieren sind. Wenn z. B. zwei 75 Ohm-Leitungen miteinander verbunden werden, von denen die eine ein TV-Koaxialkabel ist und die andere eine mikroskopisch kleine Mikrostreifenleitung, ist der Steckerübergang nach der Leitungstheorie reflexionsfrei, in der Realität aber keinesfalls. Hier endet die Leitungstheorie und die Maxwellschen Gleichungen sind zu lösen (vergl. Hochfrequenztechnik).
Literatur[Bearbeiten | Quelltext bearbeiten]
- Heinrich Schröder: Elektrische Nachrichtentechnik, I. Band. Verlag für Radio-Foto-Kinotechnik GmbH, Berlin-Borsigwalde 1966.
- Peter Vielhauer: Theorie der Übertragung auf elektrischen Leitungen. Verlag Technik, Berlin 1970.
- Hans-Georg Unger: Elektromagnetische Wellen auf Leitungen. Dr. Alfred Hüthig Verlag, Heidelberg 1980, ISBN 3-7785-0601-3.
- Claus-Christian Timmermann: Hochfrequenzelektronik mit CAD, Band 1. Leitungen, Vierpole, Transistormodelle und Simulation mit numerischen und symbolischen CAD/CAE-Systemen. PROFUND Verlag, Plankstadt 2003, ISBN 3-932651-21-9.
- Gerhard Wunsch: Geschichte der Systemtheorie. Akademie-Verlag, Leipzig 1985.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Literatur über Leitungstheorie im Katalog der Deutschen Nationalbibliothek
- Skript zur Vorlesung „Elektronik“ von Prof. Dr. Klaus Wille, Technische Universität Dortmund ( vom 24. Januar 2014 im Internet Archive) (PDF; 1,5 MB)
Einzelnachweise[Bearbeiten | Quelltext bearbeiten]
- ↑ Timmermann: Hochfrequenzelektronik mit CAD, Band 1. (Lit.), S. 123 ff.
- ↑ Timmermann: Hochfrequenzelektronik mit CAD, Band 1. (Lit.), S. 156–160 ff.
- ↑ R. Busch: Elektrotechnik und Elektronik, 7. Auflage, Springer Vieweg 2015, ISBN 978-3-658-09674-8








































































