Diskussion:Winkelgeschwindigkeit
|
Dieser Artikel wurde ab Januar 2011 in der Qualitätssicherung Physik unter dem Titel „Winkelgeschwindigkeit vs. Kreisfrequenz“ diskutiert. Die Diskussion kann im Archiv nachgelesen werden. Anmerkung: Abgrenzung Winkelgeschwindigkeit vs. Kreisfrequenz (150kB) |
|
Dieser Artikel wurde ab Februar 2013 in der Qualitätssicherung Physik unter dem Titel „Winkelgeschwindigkeit vs. Kreisfrequenz“ diskutiert. Die Diskussion kann im Archiv nachgelesen werden. Anmerkung: Abgrenzung Winkelgeschwindigkeit vs. Kreisfrequenz (77kB) |
f definieren
[Quelltext bearbeiten]im artikel wird f als formelzeichen verwendet bevor es definiert wird, es ist aber vorher schon die Rede von der Frequenz (das die BEdeutung von f doch, oder?), müsste man nur hintendranschreiben, falls ich das richtig überblicke... lg phil--90.136.128.135 21:01, 13. Jul. 2009 (CEST)
- (Neue Punkte bitte unten anfügen, nicht oben.) Danke für den Hinweis. Weiter unten wurde es schon erläutert, das weiter oben stehende Vorkommen ist wohl erst später dazugekommen. --PeterFrankfurt 00:54, 14. Jul. 2009 (CEST)
inhaltlicher Fehler?!
[Quelltext bearbeiten]Ich halte folgende Aussage für falsch: "Die Winkelgeschwindigkeit ist proportional zur Kreisfrequenz (Frequenz der Bewegung bzw. Drehzahl), eignet sich jedoch für physikalische Berechnungen besser."
Die Winkelgeschwindigkeit ist die Kreisfrequenz. Bei einer Kreisbewegung heißt sie Winkelgeschwindigkeit, bei einer harmonischen Schwingung ist es die Kreisfrequenz. Hier ist eingentlich die Frequenz der Bewegung gemeint, diese ist proportional zur Winkelgeschwindigkeit (Kreisfrequenz). Wbetz 19:23, 11. Jul. 2009 (CEST)
- (Neue Punkte bitte unten anfügen, nicht oben.) Genau. Es ist ein sprachlicher Fehler, weniger ein sachlicher. In der Klammer dahinter wird es richtiggestellt. Aber den Begriff "Kreisfrequenz" darf man da nicht verwenden, das ist missverständlich. Das müssen wir umformulieren. --PeterFrankfurt 01:29, 12. Jul. 2009 (CEST)
Was ist denn das?
[Quelltext bearbeiten]Winkel kann man nie als Vektor darstellen. Rausgenommen. --Hubi 10:44, 1. Apr 2005 (CEST)
- Wieso nicht? Die Richtung ist die Rotationsachse, der Betrag ist die Größe des Winkels - oder wie willst du sonst zu kommen? Die Formel ist trotzdem entbehrlich, da Grundlage der Infinitisimalrechnung --Langläufer 16:09, 2. Apr. 2008 (CEST)
- Welcher Winkel soll denn abgeleitet werde, damit man zu omega kommt. Wurde schon 2005 festgestellt, dass phi kein Vektor sein kann. Jetzt ist es ein Skalar. Macht die Sache aber nicht besser. Man müsste ja die Rotationsebene schon kennen wenn man in der einen Winkel messen wollte. Dan hätte man aber schon die Richtung, vorgegeben. In der Form gilt das nur für ebene Drehungen.--Wruedt 22:11, 28. Feb. 2011 (CET)
- Ein Blick in Drehmatrix würde vielleicht helfen dieses Wirrwarr etwas zu lichten. Hier wird die infinitesimale Drehung erklärt, über die Ableitung der Drehmatrix. Ähnliches siehe Quelle Rill. Man müsste nur Gl. 2.83 zur Kenntnis nehmen, da steht drin wie man aus der Ableitung von Kardanwinkeln zu Drehgeschwindigkeiten kommt. Von diesen Winkeln gibt's immerhin 3.--Wruedt 23:04, 28. Feb. 2011 (CET)
Erweiterung
[Quelltext bearbeiten]Wie sieht das mit Drehungen um mehrere Achsen aus? Wenn die Matrix A(t) eine von t abhängige Rotationsmatrix ist, dann ist doch die Winkelgeschwindigkeit
mit
___________________________________
Ich glaube euch, dass das so richtig ist. Aber für Ottonormalmensch hättet ihr die Formeln auch gleich weglassen können.
- Für (Physik-)Studenten nicht.
Vereinfachung
[Quelltext bearbeiten]Was soll denn dieses d"Kauderwelsch" bedeuten??? Könnte das mal jemand noch für die Dummen dieser Welt etwas ausführen?!
Gemacht.
Beispiel: Rennautos auf einem Rundkurs. "An die Stelle der zurückgelegten Strecke tritt der Drehwinkel, der im Kreis zurück gelegte Winkel. Die Winkelgeschwindigkeit drückt aus, welchen Winkel ein Gegenstand pro Sekunde überstreicht, und die Winkelbeschleunigung gibt die zeitliche Änderung der Winkelgeschwindigkeit an." aus Physik für Dummies, Kap. 7
Und ich muss sagen, dass hilft mir mehr als das Spezialisten GeRede hier. Vielleicht sollte man bei solchen Einträgen von der simplen (vereinfachten) Darstellung zur ausführlichen übergehen. Wäre das nicht fúr alle von Vorteil!!! Vergesst nicht, dieses Thema ist auch noch in der Schule dran und man sollte die Leute nicht immer verschrecken!!! --ostlicht 21:01, 22. Sep. 2007 (CEST)
inhaltliche Frage
[Quelltext bearbeiten]Ich finde das ganze ziemlich verwirrend... was ist denn nun der Unterschied zwischen Kreisfrequenz und Winkelgeschwindigkeit?
Die Winkelgeschwindigkeit der Kreisbewegung ist die Kreisfrequenz * 2pi... (grob gesagt) Die Winkelgeschw. gibt den überstrichenen Winkel pro Zeit an. Die Frequenz hingegen die Umdrehungen pro Zeit. Da eine Umdrehung zwei pi sind, folgt der Zusammenhang wie oben beschrieben.
Genau, eigentlich ist alles eine Sache der Bequemlichkeit. Die intuitive Größe ist die Frequenz = Zahl der (Schwingungen, Umläufe, etc.) pro Zeiteinheit. Damit handelt man sich aber in vielen Gleichungen Faktoren ein, z.B. . Daher ist es einfacher und übersichtlicher, die Winkelgeschwindigkeit zu verwenden. Weitere Geheimnisse verbergen sich nicht dahinter. --Heiko Schmitz 11:08, 14. Aug 2006 (CEST)
Hallo, warum steht da, das es keinen Zusammenhang mit dem Radius gibt, wo mir die Formel w=v/r bekannt ist?
- Weil im v indirekt auch wieder der Radius drinsteckt. Und anders: In der Formel ω=v/r stehen auf der rechten Seite gleich zwei Variablen, das ist prinzipiell unübersichtlicher; bei ω=2πf steht rechts nur noch eine Variable, und es ist eindeutig, worum es geht. --PeterFrankfurt 02:33, 19. Mär. 2009 (CET)
(Weitergeleitet von Rotationsgeschwindigkeit)
[Quelltext bearbeiten]Ich wollte etwas über die Messbarkeit der Rotationsgeschwindigkeit von Planet Erde erfahren, lande leider hier bei der nichtmessbaren Winkelgeschwindigkeit. Was nun? Danke. --85.212.182.136 13:04, 21. Okt. 2006 (CEST)
- Kann mir niemand weiterhelfen bitte? Ich habe doch mit vier Tilden unterschrieben. --85.212.144.108 01:40, 22. Okt. 2006 (CEST)
- Daran lag es bestimmt nicht. Schau mal bei Erdrotation --Tinz 01:41, 22. Okt. 2006 (CEST)
- Ich verstehe nicht ganz, was du meinst, insbesondere mit "Messbarkeit" und "Rotationsgeschwindigkeit". Versteht man unter Rotationsgeschwindigkeit die Zeit für eine vollständige Umdrehung um die eigene Achse der Erde, so ist klar, dass diese 1 Tag, also 24h beträgt, genauer 1/365 weniger (etwa 4 Minuten) wegen der Rotation um die Sonne. Ist die Zeit für eine vollständige Umdrehung um die Sonne gemeint, so ist dies 365,2?? Tage. Ist die Geschwindigkeit eines Punktes auf der Erdoberfläche gemeint, so ist diese Null am Pol, und ca. 40000km/24h am Äquator (etwa 1666 km/h oder 460 m/s), an anderen Punkten etwa 40000km/24h*cos(Breitengrad). Dies erhält man durch theoretische Überlegungen, nicht (direkt) über Messgeräte. Messen lässt sich die Zeit für eine Umdrehung mit einer Uhr und Beobachtung der Sonne, der Erdumfang über die gemessenen Winkel der Sonnenstrahlung zu gleicher Zeit an verschiedenen Breitengraden (historisch etwa durch Erathostenes in Syrene und Alexandria). --Hubi 08:55, 22. Okt. 2006 (CEST)
- Die Winkelgeschwindigkeit der Erdrotation um die eigene Achse kann man ebenfalls als Rotationsgeschwindigkeit bezeichnen. Diese ist ziemlich genau (2 pi)/(1 Tag) - etwas genauer 1/365,2??? weniger, siehe oben. Dazu benötigt man interessanterweise (!) gar keine Messgeräte (da man die Zeiteinheit ja als Teil eines Tages auffasst). Genaues Beobachten reicht (zusammen mit einem korrekten Modell der Welt/des Planetensystems). --Hubi 09:08, 22. Okt. 2006 (CEST)
Definition
[Quelltext bearbeiten]Der Begriff "Winkelgeschwindigkeit" wird hier ausschließlich in Bezug auf eine Kreisbewegung (Rotation) definiert, aber bei den Planetenbahnen spricht man doch auch von Winkelgeschwindigkeit. Das ist für mich als Laien verwirrend. Nwabueze 14:58, 30. Mär. 2008 (CEST) Die Winkelgeschwindigkeit ist bei Planeten nicht konstant. An der Definition, Winkeländerung pro Zeit ist m.E. aber nichts auszusetzen. --Langläufer 15:57, 2. Apr. 2008 (CEST)
- An diesem Aspekt der Definition setze ich nichts aus, aber wenn in der Definition steht bei einer Kreisbewegung (Rotation), kann der Leser das so verstehen, daß der Begriff bei nicht kreisförmigen Bewegungen (Planeten) nicht zulässig ist, weil die dann nicht unter die Definition fallen. Nwabueze 16:51, 2. Apr. 2008 (CEST)
In der Gleichung v=omegaxr (vektoriell) wird v als Bahngeschwindigkeit bezeichnet. Das gilt aber nur, wenn der Ursprung des Systems in Ruhe ist. Zu dieser Geschwindigkeit müsste man die Geschwindigkeit des Ursprungs addieren. Beispiel PKW. Der hat ein körperfestes Koordinatensystem in dem die Drehgeschwindigkeit dargestellt wird (Gier- Nick- Wankgeschwindigkeit) Die Bahngeschwindigkeit eines Punkts hinter der hinteren Stoßstange ist v_b+omegaxr_rel, mit r_rel Vektor vom z.B. Schwerpunkt des Fzg's zum Mess-Punkt. Praktische Anwendung: Messung des Schwimmwinkels mittels Korrevit. --Wruedt 12:58, 5. Feb. 2011 (CET)
Zusammenlegung mit Kreisfrequenz
[Quelltext bearbeiten]Ich habe von Kreisfrequenz einen Redirect hierher gemacht und ein paar Aussagen übernommen. Große Teile habe ich aber nicht übernommen, da sie redundant sind, speziell die Ausführungen über das Pendel und den Schwingkreis, dafür habe ich die unter Anwendungen genannt. Bitte schaut mal in der letzten Version von Kreisfrequenz ob ich irgendwas wichtiges vergessen habe. Außerdem sollte dieser Artikel nochmal durchgegangen werden. --Siehe-auch-Löscher 10:58, 4. Dez. 2008 (CET)
- Vielleicht noch den Zusammenhang mit der Frequenz 2πf ? --Langläufer 14:29, 4. Dez. 2008 (CET)
Recht rund jetzt, der Artikel. Danke für die gute Zusammenarbeit. --Siehe-auch-Löscher 22:18, 5. Dez. 2008 (CET)
- Der Artikel "Kreisfrequenz" wurde hierhin umgeleitet. Jetzt müssten periodische Vorgänge (Schwingungen), bei denen die Kreisfrequenz wichtig ist, auch aufgeführt werden. Ich habe dies mit dem Abschnittchen zu Schwinungen mit der Frequenz und der Kreisfrequenz versucht, aber Benutzer Siehe-auch-Löscher besteht auf seiner Formulierung.
- Ich bin der Meinung, mit dem jetzigen Satz "Wird eine Kreisbewegung als Schwingung interpretiert, ..." hat man die meisten Schwinungen nicht erfasst. Es gibt beliebig viele periodischen Vorgänge, die NICHT Kreisbewegungen sind. Mein Abschnitt war etwas wie:
- Bei Schwingungen beschreibt die Frequenz die Anzahl Zyklen pro Zeit.
- In jedem Zyklus durchläuft das Argument der sin-/cos-Funktion den Bereich . Daraus ergibt sich die Kreisfrequenz:
- Der Ausdruck für die Frequenz ist analog zum Ausdruck für die Drehzahl:
- ´
- Ich denke, dies ist das Minimum, wie man die Schwinungen (nicht die Kreisbewegungen) erfassen sollte. Es gäbe sicher auch noch bessere Formulierungen. Zudem sollte man die Schwingungen explizit in der Einleitung erwähnen.
- --Studi111 17:48, 6. Dez. 2008 (CET)
- Das war ein Versehen. Hab's wieder hingedreht. Aber man sollte das ganze vielleicht auf harmonische Schwingungen beschränken, oder? --Siehe-auch-Löscher 21:05, 6. Dez. 2008 (CET)
Jetzt ist glaube ich was falsch:wiederspricht zumindest stark dem Inhalt vor dem Zusammenlegen sowie dem en-Artikeln. Die (Dreh-)frequenz wird nicht auch als Kreisfrequenz oder Winkelfrequenz bezeichnet.
- Ich gebe meinem Vorredner völlig recht. Die Weiterleitung nach Winkelgeschwindigkeit ist nicht gerechtfertigt. Wenn man die obigen Formulierungen eingesetzt, wäre der Artikel dich in Ordnung. Da Zusammenlegen stiftet nur Verwirrung, da Kreisfrequenz im Kontext von Schwingungen (translatorisch oder rotatorisch) verwendet wird und eben nicht nur die Bedeutung einer Drehzahl hat. --Wruedt 12:33, 29. Jan. 2011 (CET)
Die Fortsetzung der Diskussion findet nun unter Diskussion:Kreisfrequenz statt. --Siehe-auch-Löscher 20:36, 31. Jan. 2011 (CET)
Gedankenexperiment
[Quelltext bearbeiten]Folgendes Gedankenexperiment als Denkanstoß: Würde man einen Körper rund 172,8 Astronomische Einheiten (ca. 2,59*1010 km) von der Erde entfernt platzieren und beide mit einer steifen Stange verbinden, so würde dieser Körper theoretisch (!!!) Lichtgeschwindigkeit erreichen. Bei einer Winkelgeschwindigkeit von 1/s wäre hingegen "nur" eine Stange mit der Länge von 300000 km nötig, was nicht ganz der Entfernung Erde-Mond entspricht...
- Also ehrlich gesagt erscheint mir das nicht so sehr intuitiv, da die Distanzen in beiden Fällen (im zweiten immerhin fast bis zum Mond) auch schon kaum konkret vorstellbar groß sind. --PeterFrankfurt 23:02, 28. Mär. 2009 (CET)
großes Omega?
[Quelltext bearbeiten]In der Box wird als Symbol ebenfalls der große Buchstabe Omega aufgeführt. Ich kann mich nicht erinnern, dem in diesem Zusammenhang jemals über den Weg gelaufen zu sein. Kann da jemand was beisteuern, wo der verwendet werden soll? Sonst sollte man den besser löschen. --PeterFrankfurt 18:16, 16. Mai 2009 (CEST)
Großes Omega wird im Zusammenhang mit Schwingungen pro Längeneinheit benutzt (Wegfrequenz). Da hier aber nur von zeitlichen Abhängigkeiten die Rede ist, sollte man's streichen. --Wruedt 15:30, 29. Jan. 2011 (CET)
Achterbahn
[Quelltext bearbeiten]Das mit dem Achterbahnbild glaube ich irgendwie nicht so richtig. Ich habe den Verdacht, dass die Unschärfe auf den hinteren Plätzen vorwiegend die Köpfe der Passagiere betrifft und mehr auf Schütteln als auf Winkelgeschwindigkeit zurückzuführen ist. Und selbst wenn, dann ist der Effekt so minimal, dass er kaum zu einer Verdeutlichung oder Veranschaulichung taugt. --PeterFrankfurt 01:55, 18. Mai 2009 (CEST)
Glauben sollte man in der Physik nicht anwenden, Wissen ist besser. Wenn man in der Analysen die Bewegung von oben sieht, dann wird klar, dass der Zug am Anfang sich (fast) genau auf den Betrachter zu bewegt, am End aber eine fast eindeutige Querbewegung erfolgt. Und das kommt bei dem Bild wunderbar heraus, wie man auch an den Kanten der Wagen erkennt. Rolf S 17:02, 24. Mai 2009 (CEST)
- Das Beispiel Achterbahn illustriert Bewegungsunschärfe. Sicherlich lässt sich eine Betrachtungswinkeländerung je Zeiteinheit heranziehen um den Effekt zu erklären - ist allerdings ein schlechtes Beispiel für Winkelgeschwindigkeit (~ Rotationsgeschwindigkeit) --Langläufer 20:56, 24. Mai 2009 (CEST)
Winkelgeschwindigkeit und Hertz
[Quelltext bearbeiten]Es steht geschrieben, man dürfe die Einheit Hertz nicht verwenden. Es würde mich mal interessieren, warum. Auf jeden Fall sollte es für diese Aussage einen Beleg oder eine Begründung geben, die auch im Artikel angegeben werden sollte. Ich zumindest finde die Aussage recht pauschal und würde mich deshalb sehr für die Begründung interessieren. --87.172.208.217 17:26, 12. Dez. 2009 (CET)
- Die Begründung steht ein paar Sätze drüber. Ich hab es noch mal deutlicher herausgearbeitet. ThomasStahlfresser 17:38, 12. Dez. 2009 (CET)
t nicht T ist Symbol der Zeit
[Quelltext bearbeiten]Warum wird hier ein großes T benutzt, wenn es um die Zeit und nicht die Temperatur geht? (nicht signierter Beitrag von 130.75.157.196 (Diskussion | Beiträge) 15:51, 11. Feb. 2010 (CET))
- Warum? Weil es jemand falsch reingeschrieben hat, und weil wir Deppen, die wir den Artikel auf der Beobachtungsliste haben, es ständig überlesen haben. ;-) Danke für die Korrektur. ThomasStahlfresser 16:37, 11. Feb. 2010 (CET)
- Nein, weil es sich hier nicht wie in den Zeilen zuvor um eine Variable, sondern gemäß Text um die Umlaufzeit (oder Periodendauer) handelt, die mit T angegeben wird. --Saure 17:23, 11. Feb. 2010 (CET)
- Wenn in die in der Einleitung stehende Formel ω = φ / t im Zähler der konkrete Wert eines Umlaufes, φ = 2π, eingesetzt wird, muss auch im Nenner der zugehörige Wert eines Umlaufes, t = T, eingesetzt werden. --Saure 18:03, 11. Feb. 2010 (CET)
- Sorry, du hast natürlich recht. Ich war zu flüchtig in meinem Versionsvergleich und dachte es geht um
- Weiss auch nicht, was ich da gesehen haben. ThomasStahlfresser 18:12, 11. Feb. 2010 (CET)
Def. Kreisfrequenz?
[Quelltext bearbeiten]"Die Winkelgeschwindigkeit ist identisch der Kreisfrequenz ... " Dieser Satz hat nur Sinn, wenn die Kreisfrequenz definiert ist; Kreisfreqzuenznist aber nur iéin Redirect zu Winkelgeschwindigkeit. Dies stört --888344
Und was ist dann dei sog. Kreisfrequenz?
[Quelltext bearbeiten]"Bei Schwingungen und Wellen mit der Einheit Hertz liegt keine Kreisbewegung vor. Trotzdem wird ebenfalls häufig mit der Winkelgeschwindigkeit ω gerechnet. Der Grund liegt in einer gewissen Bequemlichkeit" ???????? --888344
- Steht doch direkt dahinter: Die Frequenz kommt in Formeln häufig mit dem Faktor 2pi davor vor. Und dann schreibt man statt 2*pi*f einfach omega, als bequeme Abkürzung, obwohl es mit Kreisen arg wenig zu tun hat. Es ist kürzer, die Formel wird einfacher und übersichtlicher, und man kann sie sich besser merken. --PeterFrankfurt 01:12, 30. Jul. 2010 (CEST)
Der Unterschied zwischen Kreisfrequenz und Frequenz sind die 2pi (Mitscke). Also kann man die beiden sprachlich leicht auseinander halten. Frequenz==Anzahl Schwingungen pro s, Kreisfrequenz=2*pi*Anzahl Schwingungen pro s. --Wruedt 19:51, 5. Feb. 2011 (CET)
Darstellung als Vektor
[Quelltext bearbeiten]"Dazu wird meistens die Drei-Finger-Regel angewandt." Ist das nicht zu ungenau? Entweder Rechte-Hand oder Linke-Hand und auf der Seite der Drei-Finger-Regel fand ich auch keinen Hinweis darauf, welcher Finger für welchen Vektor verwendet wird.-- Sven (nicht signierter Beitrag von 213.23.255.223 (Diskussion) 10:26, 18. Aug. 2010 (CEST))
- Sag mal...
- Hast du den Artikel Drei-Finger-Regel gelesen. Ganz sicher nicht im Sinne "verstehendes Lesen":
- Die Drei-Finger-Regel wird zur geometrisch anschaulichen Bestimmung der Orientierung dreidimensionaler :Vektoren in Rechtssystemen verwendet. Die Drei-Finger-Regel wird auch als UVW-Regel, FBI-Regel und Rechte-Hand-Regel
- Rechte-Hand-Regel steht da gleich am Anfang. Welche Fingerlein verwendet werden, dafür gibt es sogar ein Bild. Brauch'ste nich' lesen. ThomasStahlfresser 12:21, 18. Aug. 2010 (CEST)
Neuste Änderungen
[Quelltext bearbeiten]Im Moment wird bei der Kreisfreuenz schon wieder einiges Durcheinander gewurfen. Die Kreisfrequenz 2Pi/T tritt auch bei nicht konstanter Rotation auf (z.B. Keplerproblem, weil da trotzdem noch eine im Mittel gleichförmge Rotation auftritt) - so wie es in meinem Entwurf stand (Formulierung kann man natürlich ändern, aber bitte nicht den Inhalt dabei durcheinanderhauen). Sobald sich irgendein Winkel mit der Zeit in einer Periode um genau 2 Pi/T ändert, nennt man das Teil Kreisfrequenz. Dabei ist es egal, ob der Winkel als allgemeines Argument von irgendeiner Winkelfunktion (Sinus, Eulerformel, ...), als verallgemeinerte Koordinate oder als ganz "normaler" Winkel im R^3 in irgendeiner beliebigen Anwendung auftritt.
- Kreisfrequenz hat mit Rotation zunächst mal nicht das geringste zu tun. Der Begriff wird im Kontext von Schwingungen verwendet. Dort ist es üblich Systeme mit konstanter Erreger-Kreisfrequenz anzuregen. Lineare Schwingungssystem zeichnen sich durch Eigen-Kreisfrequenzen aus. Wie sich die Winkelgeschwindigkeit irgenwelcher Systeme mit der Zeit ändert ist eine andere Geschichte. Z.B. bei der Fahrt von A nach B mit dem PKW gibt es eine zeitlich veränderliche Giergeschwindigkeit, aber keine Kreisfrequenz, auch wenn das Auto zufällig im Kreis fährt. Die einzige Analogie zur Winkelgeschwindigkeit ist der besagte Zeiger in der komplexen Ebene. Näheres z.B. Mitschke Schwingungen, andere Lehrbücher zum Thema Schwingungen gibt's sicher auch. Physik-Lehrbücher sind mE nur bedingt geeignet, da wenig Praxisbezug. --Wruedt 23:47, 5. Feb. 2011 (CET)
Was ist denn an der absolut allgemeinen Definition so schwer zu verstehen? In diese Definition geht überhaupt nicht ein, um was für einen Winkel es sich handelt. Aber wie in der QS gesagt, an dem Artikel ändere ich jetzt nichts mehr. --Stefan 13:35, 5. Feb. 2011 (CET)
Bei z.B. kann ich die Definiton der Winkelgeschwindigkeit auf beide Phis anwenden. Und bei sehr vielen (wahrscheinlich fast allen) Anwendungen stellt sich heraus, dass Die Ableitung von Phi_2 = 2Pi/T ist. Und bei perfekten kreisbewegungen realer Massen stellt sich heraus, dass da auch die ABleitung von Phi_1 = 2Pi/T ist. --Stefan 13:49, 5. Feb. 2011 (CET)
Die Diskussion scheint sich tatsächlich etwas gelohnt zu haben. Der Artikel ist besser geworden. Bei der Vektordarstellung könnt man aber schon noch etwas ausholen. Hinweis auf den schiefsymmetrischen Tensor (siehe Erweiterung). Quelle hierzu: [1] Seite 21, Gleichung 2.72. --Wruedt 14:38, 5. Feb. 2011 (CET)
- Da kann man sicher noch einiges sagen. Ziel der Diskussion war aber, zu klären, ob Kreisfrequenz und Winkelgeschwindigkeit zusammengehören oder nicht. --Stefan 18:16, 5. Feb. 2011 (CET)
Beim Bild mit dem Zeiger in der komplexen Ebene sollte statt phi, das sonst nirgend vorkommt omega*t stehen. Der Zeiger dreht sich schließlich mit der Winkelgeschwindigkeit omega in der komplexen Ebene wenn die Erreger-Kreisfrequenz omega=konstant ist. Noch'n Wunsch: da müssen dringend auch mal Ingenieure z.B. aus dem Fachgebiet Schwingungen, E-Technik reinschauen. Man kann das Thema ganz offensichtlich ohne Praxisbezug nicht behandeln. --Wruedt (22:42, 5. Feb. 2011 (CET), Datum/Uhrzeit nachträglich eingefügt, siehe Hilfe:Signatur)
Die Definition delta phi/ delta t greift doch nur bei konstanter Winkelgeschwindigkeit, also warum steht das alternativ auch noch da? Eine Gleichung reicht doch. --Wruedt 10:16, 6. Feb. 2011 (CET)
Danke an alle für die noch neueren neuesten Änderungen. Mitlerweile gefällt mir der Artikel ausgesprochen gut. :) --Stefan 10:54, 6. Feb. 2011 (CET)
Dass Kreisfrequenz jetzt direkt hinter Definition kommt ist sehr unglücklich. Ausserdem steht jetzt im Abschnitt Kreisfrequenz, zählt man die Anwendung noch dazu fast mehr drin als im eigentlichen Artikel über Winkelgeschwindigkeit. Das rechtfertigt doch im Nachhinein die Forderung nach einem eigenen Artikel für Kreisfrequenz. Nur würd man dann feststellen, dass der Hauptartikel Winkelgeschwindigkeit etwas dürftig wird. --Wruedt 11:09, 6. Feb. 2011 (CET)
Wie schon angemerkt passt das Bild jetzt nicht mehr zum Text. Der Winkel phi taucht nirgends auf (wird auch nicht benötig) Statt dessen wird auf die Winkelgeschwindigkeit des Zeigers hingewiesen, und grad die fehlt im Bild. --Wruedt 11:17, 6. Feb. 2011 (CET)
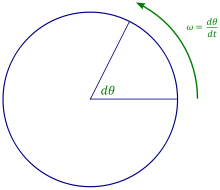
- Das Bild ist sicher nicht perfekt geeignet (war das erstbeste, dass ich gefunden hab), aber die Roration mit der Zeit wird immerhin dargestellt. Vielleicht findet sich irgendwo noch ein besseres. Auf der englischen WP (en:Angular frequency) ist das Bild rechts da. Dort geht aber leider die komplexe Ebene nicht ein. --Stefan 11:24, 6. Feb. 2011 (CET)
Dieses "kramphafte" Bemühen die Winkelgeschwindigkeit und jetzt noch die 3. Dimension reinzubringen, wird dem Thema nicht gerecht. Wer Kreisfrequenz sucht möchte nicht kleinliche Wortklaubereien, sondern knappe, präzise, korrekte Informationen über den speziellen Begriff und keine Auslassungen über alles und jedes. Es sollten sich nicht nur Physiker zu Wort melden, sondern auch Fachleute in den angewandten Naturwissenschaften (E-Technik, Maschinenbau) um den Praxis-Kontext reinzubringen. --Wruedt 08:06, 7. Feb. 2011 (CET)
- Wir schreiben hier aber nicht für Fachpublikum, das das eh schon alles weiß. Und wo die Größe angewendet und benutzt wird steht teilweise unter der Überschrift "Anwendungen und Beispiele" - dort kann jeder Ingenieur, Physiker, E-Techniker, Mathematiker, Karusselbauer, ... meinetwegen seine Lieblingsanwendung reinschreiben. Das ändert aber nichts daran, dass alle diese Größen gleich definiert sind und nur zufälligerweise mit anderen Wörtern (aber nicht Lemmas!) benannt sind. --Stefan 09:52, 7. Feb. 2011 (CET)
- Das haben wir doch zur Genüge rauf und runter debattiert. Die Begriffe werden im jeweilig passenden Kontext benutzt. Eine periodische Änderung der Luftdichte ist schließlich keine Drehzahl. --Wruedt 20:22, 7. Feb. 2011 (CET)
- Behauptet doch auch niemand (seit wann geht'S hier eigentlich um Drehzahl?). Das ist halt irgendeine Schwingung von irgendwas. Aber das Argument des Sinus der Lösung des Problems ist ein Winkel, der sich mit der Zeit ändert und damit eine Winkelgeschwindigkeit. --Stefan 09:34, 8. Feb. 2011 (CET)
Weiterleitung von Kreisfrequenz
[Quelltext bearbeiten]Die Weiterleitung von Kreisfrequenz auf diesen Artikel [2] ist eine Zumutung für jeden, der mehr über die Kreisfrequenz einer Schwingung erfahren will. Der Abschnitt "Definition" behandelt ausschließlich den Begriff Winkelgeschwindigkeit. Das ist eine grobe Irreführung. Der Abschnitt "Kreisfrequenz" versucht krampfhaft einen Begriff aus der Schwingungslehre mit Begriffen für eine Kreisbewegung zu beschreiben um den grundlegenden Unterschied zwischen Rotation und Schwingung zu verschweigen und die Darstellung der Kreisfrequenz als "Spezialfall der Winkelgeschwindigkeit" zu rechtfertigen. Die Kreisfrequenz ist aber ebenso wenig ein Spezialfall der Winkelgeschwindigkeit, wie die physikalische Schwingung ein "Spezialfall" der physikalischen Rotation ist. Insgesamt kann man die Weiterleitung von Kreisfrequenz auf diesen Artikelversuch und die Darstellung im Abschnitt "Kreisfrequenz" nur als groben Unfug bezeichnen. -- Pewa 02:07, 6. Feb. 2011 (CET)
Euler'sche Formel
[Quelltext bearbeiten]Ist die Formel sin(omega*T) wirklich e hoch j omega? e±j omega t=cos (omega T)±jsin(omega T) Das ist ja grad die Analogie zwischen Schwingung und komplexer Ebene. --Wruedt 10:05, 6. Feb. 2011 (CET)
- Nein, das ist natürlich nicht dasselbe, die harmonische Schwingung wird nur durch den Realteil der Funktion mathematisch modelliert. Das ist nur ein mathematisches Modell für die Projektion einer rotierenden Masse, die ebenfalls eine Sinusschwingung ergibt. Diese krampfhaften und grob fehlerhaften Versuche physikalisch eine rotierende Masse mit ihrer Projektion gleichzusetzen oder mathematisch einen rotierenden Zeiger in der komplexen Ebene mit seinem Realteil gleichzusetzen, nehmen hier langsam absurde Formen an. -- Pewa 16:02, 7. Feb. 2011 (CET)
Unterschied zu Kreisfrequenz
[Quelltext bearbeiten]Nach anstrengender Diskussion mit Meinungsbild befand die Mehrheit, dass Kreisfrequenz ein eigener Artikel sein sollte. Stellt sich die Frage wie's mit Winkelgeschwindigkeit weitergeht. Momentan steht 1 zu 1 der Inhalt von Kreisfrequenz drin. Das sollte so nicht bleiben. Auch gibt's keinen Link zu Kreisfrequenz.
Im übrigen stellt sich raus, dass Winkelgeschwindigkeit ein relativ dünnes Brett wird. Z.B. welcher Winkel ändert sich bei der Rotation eines Backsteins im Weltall (Euler, Kardan, ...)? Trotz Hinweis auf die Vektoreigenschaft wird im wesentlichen die ebene Drehung beschrieben. Beim Vektor sollte die Relativbewegung rausgestellt werden (fehlt auch bei den Begriffen Drehbewegung, Rotation, Drehachse, die alle bei Rotation Phyik landen). Der schiefsymmetrische Tensor deutet ja schon an, dass die omega's die dort vorkommen Komponenten im körperfesten Koordinatensystem sind. In typischen Anwendungen gilt eben auch nicht v=omega x r, sondern v= v_0+ omega x r_rel. Man trennt also Translation und Rotation (Beispiel Autorad). --Wruedt 08:25, 22. Feb. 2011 (CET)
- Bis auf einen Satz mit Link, evtl. ganz oben wie in en:Angular velocity, kann die Kreisfrequenz hier raus.
- Der Backstein rotiert in Bezug auf ein Inertialsystem, vorzugsweise ein Inertialsystem in dem der Schwerpunkt des Backsteins ruht. Es sollte erwähnt werden, dass eine konstante Winkelgeschwindigkeit für einen mit konstanter Drehzahl rotierenden Körper nur für einen Bezugspunkt auf der Rotationsachse angegeben werden kann. Ein v_0 braucht man dafür eigentlich nicht. -- Pewa 16:05, 22. Feb. 2011 (CET)
- Soll man beim Autorad die Winkelgeschw. auf den Boden legen, um die Translationsgeschw. der Radmitte dabei zu haben. Das wäre sehr ungewöhnlich. Die Winkelgeschw. beim starren Körper ist überall die selbe, sonst müsste man sich beim Gierratensensor Gedanken über den Ort im Fzg machen. --Wruedt 08:12, 28. Feb. 2011 (CET)
- Die Winkelgeschwindigkeit ist nur überall identisch, wenn man den Winkel entlang der Rotationsachse misst. Sobald man einen Winkel außerhalb der Rotationsachse misst, unterscheiden sich auch die Winkelgeschwindigkeiten innerhalb eines starren Körpers. Und Gierratensensoren sind tatsächlich häufig nahe des Fahrzeugschwerpunktes eingebaut, da sie die Rotationen, wo die Rotationsachse durch den Gierratensensor geht, am besten messen können.
- Wobei die Rotationsachse selber auch nicht eindeutig festgelegt ist: Geht die Rotationsachse des Mondes durch den Mond selber, durch den gemeinsamen Erde-Mond Schwerpunkt oder gar durch den Schwerpunkt des Sonnensystems? Oder womöglich durch den Schwerpunkt der Milchstraße? Das Problem ist: Egal, wo man die Rotationsachse hinsetzt, es gibt keine Achse, so dass alle Teile des Mondes bezüglich dieser Achse die gleiche Winkelgeschwindigkeit haben. (Man kann sich hier behelfen, indem man die Bewegung des Mondes als Überlappung von mehreren Winkelgeschwindigkeiten mit unterschiedlicher Rotationsachse beschreibt.) --Eulenspiegel1 20:17, 28. Feb. 2011 (CET)
- Soll man beim Autorad die Winkelgeschw. auf den Boden legen, um die Translationsgeschw. der Radmitte dabei zu haben. Das wäre sehr ungewöhnlich. Die Winkelgeschw. beim starren Körper ist überall die selbe, sonst müsste man sich beim Gierratensensor Gedanken über den Ort im Fzg machen. --Wruedt 08:12, 28. Feb. 2011 (CET)
- Wenn ein Auto stationär auf einem 40 m Radius fährt. so ist die Rotationsachse 40 m ausserhalb vom Auto. Müsste man den Gierratensensor auf einem beweglichen Ausleger befestigen? Sicher nicht. Denn schon die Eulersche Geschwindigkeitsgleichung v=v_s+omega x r sagt, dass es beim starren Körper nur EINE Winkelgeschwindigkeit für den ganzen Körper gibt. Deshalb ist es völlig wurscht, wo man den Gierratensensor einbaut. --Wruedt 13:44, 4. Mär. 2011 (CET)
- Geht die Gierachse, auf die sich die Gierrate bezieht, nicht immer durch das Fahrzeug? -- Pewa 14:07, 4. Mär. 2011 (CET)
- Wruedt, nehmen wir mal einen ganz primitiven Gierratensensor: Einen Magnetkompass. Der Magnetkompass ist ein primitiver Gierratensensor, dessen Messachse immer durch den magnetischen Nordpol geht.
- Wir befestigen im Auto drei Magnetkompasse: Einen Vorne unter der Motorhaube, einem im Zentrum und den dritten hinten im Kofferraum. Nun richten wir das Auto so aus, dass es direkt zum magnetischen Nordpol schaut. Das heißt, der magnetische Nordpol und die drei Kompasse liegen alle auf einer Linie. Jetzt drehen wir das Auto im Zentrum innerhalb von einer Sekunde um 90° im Uhrzeigersinn. Der Kompass im Zentrum hat sich um exakt 90° gedreht. Der Kompass im Kofferraum hat sich dagegen nur um 89,999° gedreht. Und der Kompass vorn unter der Motorhaube hat sich sogar um 90,001° gedreht.
- Das heißt, je nachdem wo wir unseren Magnetkompass befestigen, misst er eine andere Gierrate.
- Das gleiche gilt, wenn das Auto konstant einen Kreis mit 40 m Radius befährt: Zum einen Zeitpunkt schaut das Auto direkt in Richtung (magnetischen) Norden und alle 3 Kompasse zeigen den gleichen Winkel an. Nach T/4 zeigt der Magnetkompass im Zentrum eine Winkelveränderung von 90° an, während die anderen beiden Kompasse 89,999° bzw. 90,001° anzeigen. (Alle drei Kompasse zeigen zum magnetischen Nordpol. Daher können die drei Pfeile auch nicht parallel sein sondern haben leicht unterschiedliche Winkel.)
- Disclaimer: Die genauen Zahlen sind nicht ausgerechnet sondern nur geschätzt und hängen vom Breitengrad ab, auf dem sich das Auto befindet sowie von der Länge des Autos. Falls es für die Diskussion relevant ist, kann ich die genauen Zahlen aber auch gerne ausrechnen.
- Und ja, modernere Gierratensensoren orientieren sich nicht am Magnetfeld sondern z.B. an der Corioliskraft. Das bedeutet aber nur, dass sie eine andere Achse als Referenzsystem zur Winkelmessung verwenden. --Eulenspiegel1 15:00, 4. Mär. 2011 (CET)
- NEIN. Im Fahrzeugbau bzw. in der Luftfahrt ist es aber üblich ein fahrzeugfestes Koordinatensystem anzugeben, das seinen Ursprung im Schwerpunkt hat. Dieses Koordinatensystem hat eine Translationsgeschwindigkeit und eine Drehgeschwindigkeit rel. zum Inertialsystem. Beim Beispiel 40 m Kreis handelt es sich um eine ebene Bewegung. Hier kann die gesamte Bewegung durch eine Rotation um den Momentanpol ersetzt werden. Die Rotationsachse ist also 40 m ausserhalb. Da es beim starren Körper aber ohnehin nur EINE Winkelgeschwindigkeit gibt, ist es egal wo die Achse liegt und ein Glück für den Sensor, denn man kann ihn dahin bauen, wo es Platz hat. Anders sieht mit Querbeschleunigungssensoren aus. Diese geben unterschiedliche Werte je nach Einbauort an. --Wruedt 15:03, 4. Mär. 2011 (CET)
- Zu deinen ersten zwei Sätzen: Ja, das ist aber etwas vollkommen anderes. Bisher ging es um die Rotation einzelner Punkte. Jetzt geht es plötzlich um die Rotation eines Koordinatensystems bezüglich eines Inertialsystems. Und hier gilt tatsächlich, dass die Rotation unabhängig vom Ursprung ist.
- Zum Rest: Ja, der Momentanpol ist 40 m außerhalb. Und ja, man kann die Bewegung durch eine Rotation um dem Momentanpol ersetzen. Aber schau dir das Beispiel mit dem Magnetkompass nochmal an: Dem Magnetkompass ist vollkommen egal, wo der Momentanpol liegt. Der Magnetkompass misst nicht die Rotation bzgl. des Momentanpols sondern die Drehung bzgl. des magnetischen Nordpols. Die Lage des Magnetkompasses wäre also nur egal, wenn der Momentanpol zufällig am magnetischen Nordpol liegen würde. --Eulenspiegel1 15:26, 4. Mär. 2011 (CET)
- NEIN. Im Fahrzeugbau bzw. in der Luftfahrt ist es aber üblich ein fahrzeugfestes Koordinatensystem anzugeben, das seinen Ursprung im Schwerpunkt hat. Dieses Koordinatensystem hat eine Translationsgeschwindigkeit und eine Drehgeschwindigkeit rel. zum Inertialsystem. Beim Beispiel 40 m Kreis handelt es sich um eine ebene Bewegung. Hier kann die gesamte Bewegung durch eine Rotation um den Momentanpol ersetzt werden. Die Rotationsachse ist also 40 m ausserhalb. Da es beim starren Körper aber ohnehin nur EINE Winkelgeschwindigkeit gibt, ist es egal wo die Achse liegt und ein Glück für den Sensor, denn man kann ihn dahin bauen, wo es Platz hat. Anders sieht mit Querbeschleunigungssensoren aus. Diese geben unterschiedliche Werte je nach Einbauort an. --Wruedt 15:03, 4. Mär. 2011 (CET)
- In der Definition ist von einem schiefsymmetrischen Tensor die Rede. Dieser vermittelt das Kreuzprodukt, omega x r_rel. Dieses Kreuzprodukt taucht beim starren Körper auf, um Geschwindigkeiten bel. Punkte des Körpers berechnen zu können. Dass die Winkelgeschwndigkeit eines starren Körpers mit den Komponenten omega_x, omega_y, omega_z überall im Körper IDENTISCH ist, sollte ernsthaft keiner bestreiten. Wir reden deshalb von der Winkelgeschwindigkeit des starren Körpers, die natürlich mit der Winkelgeschwindigkeit des körperfesten Systems identisch ist. Dass die Winkelgeschwindigkeit was mit dem Nordpol zu tun hätte ist mir neu. Die Winkelgeschw. zum Nordpol hat doch nichts mit der Winkelgeschw. des starren Körpers zu tun. Wenn man ein Rechteck dreht, so ändern sich alle Winkel um den gleichen Betrag. Hab noch nie gehört, dass die Winkeländerungen in Bezug auf einen beliebig entfernten Punkt (Nordpol) gemessen werden.--Wruedt 16:00, 4. Mär. 2011 (CET)
- Die Winkelgeschwindigkeit ist in jedem Punkt eines starren Körpers identisch bezüglich des Momentanpols. Bezüglich jeder anderen Achse (bzw. jeden anderen Punktes in der Ebene) sind die Winkelgeschwindigkeiten jedoch verschieden. (Berechne doch einfach mal etwas, indem du für r_rel nicht die Entfernung zum Momentanpol sondern die Entfernung zu einem beliebigen anderen Punkt einsetzt.)
- Die Winkelgeschwindigkeit eines starren Körpers bezüglich des Momentanpols ist identisch mit der Winkelgeschwindigkeit des ortsfesten Bezugssystems bezüglich eines Inertialsystems. - Bei Winkeln und Winkelgeschwindigkeiten musst du immer sagen, worauf du dich beziehst: Winkelgeschwindigkeiten eines Punktes musst du bezüglich einer Achse angeben. Und Winkelgeschwindigkeiten eines Bezugssystems musst du bezüglich eines anderen Bezugssystems angeben.
- Doch, die Winkelgeschwindigkeit zum Nordpol hat selbstverständlich etwas mit dem starren Körper zu tun: Es ist die Winkelgeschwindigkeit des starren Körpers bezüglich des Nordpols. Und die Winkelgeschwindigkeit wird immer bezüglich des magnetischen Nordpols angegeben, wenn man mit einem Magnetkompass als Messgerät arbeitet.
- Wenn du ein Rechteck drehst, so ändern sich alle Punkte bezüglich des Momentanpols um den gleichen Betrag. Bezüglich einer beliebigen anderen Achse ändern sich die Winkel unterschiedlich. Siehe dazu auch Koordinatentransformation von kartesischen Koordinaten in Polarkoordinaten. (Oder Koordinatentransformation von Polarkoordinaten mit Z_0 als Zentrum nach Polarkoordinaten mit Z_1 als Zentrum.)
- --Eulenspiegel1 16:51, 4. Mär. 2011 (CET)
- Geb's langsam auf. Nach der Def. hätte ein geradeaus fahrendes Auto eine Winkelgeschwindigkeit, aber nur wenn es in Ost/Westrichtung fährt. Empfehle das Studium von http://books.google.de/books?id=1CnRsQCUYkIC&pg=PA35&lpg. Der Nordpol taucht jedenfalls in der Mechanik starrer Körper als Bezugsgröße für die Winkelgeschwindigkeit nicht auf.--Wruedt 18:06, 4. Mär. 2011 (CET)
- Jedes Objekt hat immer eine Winkelgeschwindigkeit bezüglich einer geeigneten Achse. Eine Auto, das in Ost-West-Richtung fährt hat eine Winkelgeschwindigkeit bezüglich der magnetischen Pole als Achse. Es hat aber keine Winkelgeschwindigkeit bezüglich des Momentanpols. Und auch wenn ein Auto in Nord-Süd-Richtung fährt, gibt es dutzende von Achsen bezüglich derer es eine Winkelgeschwindigkeit hat.
- Und natürlich taucht der Nordpol explizit nicht auf. Es ist nur einer von Abermilliarden möglichen Achsen. Erwartest du ernsthaft, dass man ein Buch herausbringt, in der man alle mögliche Milliarden Achsen auflistet? Ebensowenig gibt es ein Buch, in der alle möglichen Milliarden Inertialsysteme aufgelistet sind.
- Zur Konstanz der Winkel in deinem Link: Es geht um die Winkel innerhalb des Starren Körpers. Diese bleiben auch bei einer Rotation konstant. Wenn man die im Buch angesprochenen Winkel verändern wollte, müsste man den Körper verformen. Bei Rotationen geht es für gewöhnlich nicht um die Winkeländerung von drei Punkten innerhalb eines starren Körpers sondern um die Winkelveränderung eines Punktes (eines starren Körpers) bezüglich einer Achse. --Eulenspiegel1 18:31, 4. Mär. 2011 (CET)
- Geb's langsam auf. Nach der Def. hätte ein geradeaus fahrendes Auto eine Winkelgeschwindigkeit, aber nur wenn es in Ost/Westrichtung fährt. Empfehle das Studium von http://books.google.de/books?id=1CnRsQCUYkIC&pg=PA35&lpg. Der Nordpol taucht jedenfalls in der Mechanik starrer Körper als Bezugsgröße für die Winkelgeschwindigkeit nicht auf.--Wruedt 18:06, 4. Mär. 2011 (CET)
- In der Definition ist von einem schiefsymmetrischen Tensor die Rede. Dieser vermittelt das Kreuzprodukt, omega x r_rel. Dieses Kreuzprodukt taucht beim starren Körper auf, um Geschwindigkeiten bel. Punkte des Körpers berechnen zu können. Dass die Winkelgeschwndigkeit eines starren Körpers mit den Komponenten omega_x, omega_y, omega_z überall im Körper IDENTISCH ist, sollte ernsthaft keiner bestreiten. Wir reden deshalb von der Winkelgeschwindigkeit des starren Körpers, die natürlich mit der Winkelgeschwindigkeit des körperfesten Systems identisch ist. Dass die Winkelgeschwindigkeit was mit dem Nordpol zu tun hätte ist mir neu. Die Winkelgeschw. zum Nordpol hat doch nichts mit der Winkelgeschw. des starren Körpers zu tun. Wenn man ein Rechteck dreht, so ändern sich alle Winkel um den gleichen Betrag. Hab noch nie gehört, dass die Winkeländerungen in Bezug auf einen beliebig entfernten Punkt (Nordpol) gemessen werden.--Wruedt 16:00, 4. Mär. 2011 (CET)
Im Artikel wird z.Zt diese Fomulierung verfochten:
"Man bezieht die Frequenz eines periodischen Vorgangs auf den Kreisumfang des Einheitskreis."
Das liest sich, als ob der Kreisumfang je nach Frequenz mal größer und mal kleiner wäre, was dem "Einheitskreis" direkt im Satz widerspricht. Ist es nicht eigentlich eher so, dass:
"Man bezieht die Dauer einer Periode einer harmonischen Schwingung auf den Kreisumfang des Einheitskreises."
? --arilou (Diskussion) 09:10, 15. Feb. 2013 (CET)
Begriffserklärung
[Quelltext bearbeiten]Was ist das für eine seltsame Begriffserklärung? Wenn man was über die Rotation eines Flugzeugs erfahren möchte, muss man dank Redirekterei bei Gierachse, Querachse, Längsachse nachschauen. Für die selben Drehbewegungen beim Landfahrzeug schaut man besser bei Fahrdynamik nach. Was ist das für ein Durcheinander. Plädiere dafür die Begriffserklärung rauszunehmen und spezielle Winkelgeschwindigkeiten bei Luft- und Landfahrzeugen mit Siehe auch abzuhandeln. --Wruedt 08:03, 28. Feb. 2011 (CET)
Angular velocity
[Quelltext bearbeiten]Was spricht denn dagegen den englischen Artikel en:Angular velocity mehr oder weniger zu übersetzen. Der ist umfangreich, es steht nichts falsches drin, die Starrkörperbewegung ist vernünftig erklärt, auch die Winkelgeschwindigkeiten von Teilchen kommen auf ihre Kosten. Dagegen wirkt der deutsche Artikel etwas dürftig.--Wruedt 09:36, 5. Mär. 2011 (CET)
Erst beim Beispiel Himmelskörper tauchen die Begriffe Tangentialgeschwindigkeit und Radialgeschwindigkeit auf. Das Bild dazu gibt's erst bei Eigenbewegung. Ein Abschnitt Winkelgeschwindigkeit von Teilchen würde helfen. Spricht was dagegen, bei dieser Sachlage einen Baustein Überarbeiten oder Lückenhaft zu setzen? Werden beim einfachen Übersetzen Urheberrechte verletzt?--Wruedt 10:21, 5. Mär. 2011 (CET)
- Gegen eine Übersetzung spricht nichts. Mir gefällt der englische Artikel ebenfalls besser. Da der englische Artikel auch unter einen freien Lizenz steht, kannst du deren Texte kopieren, ohne Urheberrechte zu verletzen. Allerdings musst du in die Kommentarzeile schreiben, dass du den englischen Text kopiert hast. Alternativ kann das auch auskommentiert im Artikel selber reingeschrieben werden.
- Gegen die Bausteine spricht, dass du ja scheinbar sowieso den Artikelüberarbeiten willst. Diese Artikelbausteine setzt man, wenn man einen Artikel überarbeitungswürdig findet, selber aber keine Zeit hat, den Artikel zu überarbeiten. Daher erstmal den englischen Artikel übersetzen.Wenn anschließend noch etwas Lückenhaft ist,kann man den entsprechenden Baustein immernoch einsetzen. --Eulenspiegel1 11:43, 5. Mär. 2011 (CET)
- OK. Hab auf meiner Benutzerseite mal eine Baustelle angefangen, mit einer gekürzten Version des Abschnitts "particle in two dimensions". Da ich auch nur endlich Zeit dafür habe, müsste man ev. die Beiträge stückweise übernehmen. Würde da ein simples copy paste reichen? Was die Symbole und Schreibweisen angeht müsst man schauen, dass es mit dem bisherigen Artikel konsistent wird. --Wruedt 13:23, 5. Mär. 2011 (CET)
Winkelgeschwindigkeit des starren Körpers
[Quelltext bearbeiten]Man muss eigentlich noch dazu schreiben, dass die Winkelgeschwindigkeiten des ortsfesten Bezugsystem mit Ursprung in ist.
Sobald damit jedoch eine beliebige Winkelgeschwindigkeit von gemeint ist, gilt nicht mehr die Gleichung:
Einfaches Gegenbeispiel:
Man betrachte ein Lineal, mit den beiden Endpunkten und . Die Bewegungsgleichungen für die beiden Punkte seien:
Wie man leicht überprüfen kann, ist dies ein starrer Körper.
In diesem Fall würde jedoch gelten:
- Die Winkelgeschwindigkeit von bzgl. des Koordinatenursprunges (0,0,0) ist
- Die Winkelgeschwindigkeit von bzgl. des Punktes (1,0,0) ist auch
Aber die Gleichung
wäre offensichtlich falsch: Der Punkt P würde sich immer positiv in Richtung der y-Achse bewegen und sich bezüglich der x und z-Achse überhaupt nicht bewegen. Was jedoch im Widerspruch zu der obigen Bewegungsgleichung liegt.
Der Grund dafür liegt darin, dass nicht die Winkelgeschwindigkeit des ortsfesten Bezugssystems angibt sondern die Winkelgeschwindigkeit des Punktes bzgl. des Nullpunktes. Die Winkelgeschwindigkeit des ortsfesten Bezugssystems ist nämlich Null. Und die Translationsgeschwindigkeit des ortsfesten Bezugssystems ist . Und damit würde dann auch die obige Gleichung wieder stimmen.
Lange Rede kurzer Sinn:
Die obige Gleichung gilt nur, wenn die Translationsgeschwindigkeit bzw. die Winkelgeschwindigkeit des ortsfesten Bezugssystems sind. Besitzt man jedoch andere Translations- bzw. Winkelgeschwindigkeiten, muss man diese erst in die Geschwindigkeiten des ortsfesten Bezugssystems umrechnen. --Eulenspiegel1 00:31, 21. Mär. 2011 (CET)
- Das Lineal (der Starrkörper) in Deinem Beispiel hat die Winkelgeschwindigkeit Null. Das Lineal als ganzes wird durch 2 Hebelarme, die um (0,0,0) bzw. (1,0,0) rotieren nur translatorisch bewegt. Ähnlich der Kurbelstange einer Dampflokomotive, die 2 Räder miteinander verbindet. -- Wruedt 08:22, 22. Mär. 2011 (CET)
- Na ja, beschränken wir uns bei den allgemeinen Artikeln nicht auf den einfachen Fall des idealen "Massepunkts"? Und die Ausweitung auf einen endlich großen starren Körper überlassen wir den Studenten dann als Übungsaufgabe... Und übrigens schreibt man "läßt" heutzutage "lässt". --PeterFrankfurt 02:22, 21. Mär. 2011 (CET)
- Der Absatz stammt aus dem englischen Artikel und hieß dort ... of a particle. Ich hab das blos in Winkelgeschwindigkeit des Sehstrahls umgetauft, da der Massepunkt bekanntlich keine Winkelgeschwindigkeit hat -- Wruedt 08:08, 21. Mär. 2011 (CET)
- Alles kann eine Winkelgeschwindigket haben. Sogar ein Massepunkt. (Beispiel: Mathematisches Pendel) Wobei Winkelgeschwindigkeit des Massepunktes halt gleichgroß wie die Winkelgeschwindigkeit des Sehstrahls ist. --Eulenspiegel1 23:25, 21. Mär. 2011 (CET)
- Schau in den Artikel: "Insbesondere besitzt ein Massenpunkt keine Rotationsfreiheitsgrade" -- Wruedt 08:30, 22. Mär. 2011 (CET)
- Ein Massenpunkt besitzt in der klassischen Mechanik nur drei Freiheitsgrade. Das ist richtig. Und es stimmt ebenfalls, dass man diese drei Freiheitsgrade alle durch Translation auffüllen kann und die Rotation sich dann daraus ableitet. Aber beim Mathematischem Pendel ist es beispielsweise der Fall, dass es sich anbietet, die Freiheitsgrade mit den Winkeln zu füllen und die Translation leitet sich dann daraus ab. --Eulenspiegel1 20:27, 22. Mär. 2011 (CET)
- Schau in den Artikel: "Insbesondere besitzt ein Massenpunkt keine Rotationsfreiheitsgrade" -- Wruedt 08:30, 22. Mär. 2011 (CET)
- Alles kann eine Winkelgeschwindigket haben. Sogar ein Massepunkt. (Beispiel: Mathematisches Pendel) Wobei Winkelgeschwindigkeit des Massepunktes halt gleichgroß wie die Winkelgeschwindigkeit des Sehstrahls ist. --Eulenspiegel1 23:25, 21. Mär. 2011 (CET)
- Der Absatz stammt aus dem englischen Artikel und hieß dort ... of a particle. Ich hab das blos in Winkelgeschwindigkeit des Sehstrahls umgetauft, da der Massepunkt bekanntlich keine Winkelgeschwindigkeit hat -- Wruedt 08:08, 21. Mär. 2011 (CET)
Hallo Eulenspiegel. Wir haben das rauf und runter diskutiert. Ich möchte Dich bitten vor solchen Änderungen zunächst den englischen Artikel und dann weiterführende Literatur zu studieren (z.B. Rill). So wie's drinstand ist es Unsinn. Falls ein edit-war draus entstehen sollte bin ich dafür den Absatz lieber draussen zu lassen. -- Wruedt 07:48, 21. Mär. 2011 (CET)
Zum Inhalt wäre noch zu sagen, dass bei Anwendungen im Fahrzeugbau oder in der Luftfahrt das ortsfeste Bezugssystem wie schon der Name sagt in Ruhe ist. Relativ dazu wird die Bewegung eines starren Körpers z.B. der Aufbau einen PKW beschrieben. Dieser starre Körper besitzt ein körperfestes Koordinatensystem. Typischerweise wird der Ursprung dieses Systems in den Schwerpunkt gelegt. -- Wruedt 07:59, 21. Mär. 2011 (CET)
- Zum Inhalt: Hast du dir mein Gegenbeispiel durchgelesen? Ich würde dich bitten, dies zu tun. Und falls du der Meinung bist, dass es falsch ist, sage mir doch bitte, an welcher Stelle ich mich bei meinem Gegenbeispiel geirrt habe.
- Zumindest in der Astronomie wird nicht zwischen ortsfesten und körperfesten Bezugssystemen unterschieden: Der Planet Erde ist sowohl ein Körper als auch ein Ort. Daher kann man hier sowohl von körperfesten als auch von ortsfestem Bezugssystem sprechen. Und die Sonne ist ebenfalls sowohl ein Körper als auch ein Ort. Daher kann man auch hier sowohl vom ortsfesten als auch vom körperfesten Bezugssystem sprechen. Aber wenn du das gerne unterscheiden willst, dann kannst du das gerne machen. Dann wäre halt die Sonne das ortsfeste Bezugssystem, da näherungsweise ein Inertialsystem. Und die Erde, die um die Sonne kreist, wäre das körperfeste Bezugssystem. Das alles ändert aber nichts daran, dass man nicht die Rotation eines Körpers, sondern die Rotation des dazugehörigen Bezugssystems betrachtet. (Egal, ob man es nun als körperfest oder als ortsfest bezeichnet.)
- Ich habe mir den englischen Artikel durchgelesen. Und auch dort steht:
To obtain the equations it is convenient to image a rigid body attached to the frames and consider a coordinate system that is fixed with respect to the rigid body. Then we will study the coordinate transformations between this coordinate and the fixed "laboratory" system.
- --Eulenspiegel1 23:25, 21. Mär. 2011 (CET)
- Meinem Eindruck nach ist das Problem hier nicht, dass du evtl. falsch liegst, sondern dass du Benutzer Wruedt nicht brav um Erlaubnis gefragt hast, in "seinem" Artikel zu editieren. ÅñŧóñŜûŝî (Ð) 23:40, 21. Mär. 2011 (CET)
- Das ist nicht "mein" Artikel. Da der englische Artikel aber wesentlich mehr Informationen enthält, hab ich Teile davon übersetzt. Statt einen edit-war anzufangen, könnte man sich damit beschäftigen, wo (sinnentstellende) Fehler bei der Übersetzung passiert sind. Ansonsten braucht's vielleicht eine 3. Meinung zur Technischen Mechanik (Prof. Rill könnte man ansprechen).
Wie schon mehrfach betont. Ein ortsfestes Koordinatensystem ist in Ruhe. Was den letzten (englischen) Absatz angeht, so muss natürlich bei der Auswertung von Vektorgleichungen im Rechner ein Koordinatensystem gewählt werden, in dem die Berechnungen durchgeführt werden. Zwischen den Koordinatensystemen (Labor- und körperfest) gibt es eine Transformationsmatrix. Im Fahrzeugbau wird das Laborsystem (erdfest) auch als Inertialsystem bezeichnet, da die Erdrotation auf die Fahrdynamik einen vernachlässigbaren Einfluss hat. Das körperfeste System hat eine Geschwindigkeit (translatorisch und rotatorisch) relativ zum erdfesten System. Verschiedene Punkte im Auto sind im Fahrzeugfesten Koordinatensystem konstant, z.B. der Vektor vom Schwerpunkt zum Kofferraum. Möchte man die Geschw. eines Punkts im Kofferraum berechnen, so gilt: v_Kofferraum=v_Schwerpunkt + omkegaxr_Schwerpunkt_Kofferraum. (Eulersche Gleichung). Da das körperfeste System mit dem starren Körper verbunden ist, kann der starre Körper natürlich keine andere Winkelgeschwindigkeit als die Winkelgeschwindigkeit des körperfesten Systems relativ zum erdfesten System haben (... consider a coordinate system that is fixed with respect to the rigid body). -- Wruedt 00:17, 22. Mär. 2011 (CET)
- Ein ortsfestes Koordinatensystem ist eben nicht in Ruhe, wie mit dem Experiment des Foucaultschen Pendel gezeigt wurde. Wenn man ein ruhendes System haben will, muss man ein Inertialsystem nehmen, welches in der Regel eben nicht ortsfest ist. Mag sein, dass dies in der Fahrdynamik eine vernachlässigbare Rolle spielt. Aber in der Astronomie spielt die Erdrotation eine ganz enorme Rolle. Und der Artikel Winkelgeschwindigkeit ist nicht für Fahrzeugingenieure reserviert sondern ist für alle Fachgruppen offen, die sich mit Winkelgeschwindigkeiten befassen. Also auch für Astronomen.
- Ja, zwischen den beiden Koordinatensystemen gibt es eine Transformationsmatrix. Und die Winkelgeschwindigkeit dieser Transformationsmatrix ist es eigentlich, um die es in dem Abschnitt geht.
- Ja, das autofeste System hat eine Winkelgeschwindigkeit relativ zum erdfesten System. Aber es hat ebenso eine Winkelgeschwindigkeit relativ zum sonnenfesten System.
- Ja, das körperfeste System ist mit dem starren Körper verbunden. Dennoch enthält der starre Körper auch zahlreiche Winkelgeschwindigkeiten, die nicht im körperfesten System auftauchen. Lese dir bitte mein Gegenbeispiel weiter oben durch: Das körperfeste System dort hat eine Winkelgeschwindigkeit von Null. Aber der Körper selber hat eine Winkelgeschwindigkeit von . Das zeigt, dass ein starrer Körper und sein körperfestes System nicht zwangsläufig die gleiche Winkelgeschwindigkeit haben müssen. Und wenn du mir nicht glaubst, mache dir endlich die Mühe und lese dir mein Gegenbeispiel weiter oben durch.
- Was hat die Gleichung v_Kofferraum=v_Schwerpunkt + omegaxr_Schwerpunkt_Kofferraum bitteschön mit den Eulerschen Gleichungen zu tun? Die Eulerschen Gleichungen lauten: mit .
- Im Artikel schreibst du, dass die beiden Punkte eine Winkelgeschwindigkeit haben. Weiter oben in dieser Diskussion schreibst du jedoch, dass Massepunkte gar keine Winkelgeschwindigkeit haben können. Widersprichst du dir da nicht selber?
- --Eulenspiegel1 20:27, 22. Mär. 2011 (CET)
- Da die Diskussion hier in eine "Privatfehde" ausartet, möchte ich sie hiermit beenden. Noch 2 Bemerkungen: 1. Die Winkelgeschwindigkeit um die es in dem Artikel geht, ist natürlich relativ zu einem Bezugssystem (das steht schon in der Einleitung). Dieses Bezugssystem kann z.B. erdfest sein. Wie schnell die Erde grad durch's Weltall saust ist für die Winkelgeschwindigkeit des Monds rel. zur Erde wurscht. Wenn man die absolute Winkelgeschwindigkeit wissen wollte müsste man sämtliche Systeme zurückverfolgen bis man beim Inertialsystem angelangt ist wo auch immer das sein möge. 2. :Das Lineal (der Starrkörper) in Deinem Beispiel hat die Winkelgeschwindigkeit Null im Bezugssystem. Das Lineal als ganzes wird durch 2 Hebelarme, die um (0,0,0) bzw. (1,0,0) rotieren nur translatorisch bewegt. Ähnlich der Kurbelstange einer Dampflokomotive, die 2 Räder miteinander verbindet.
- Über Deinen Satz: "Das körperfeste System dort hat eine Winkelgeschwindigkeit von Null. Aber der Körper selber hat eine Winkelgeschwindigkeit von ω. Das zeigt, dass ein starrer Körper und sein körperfestes System nicht zwangsläufig die gleiche Winkelgeschwindigkeit haben müssen." solltest Du in aller Ruhe nachdenken. Ich verkneif mir eine Wertung, denn das könnte negativ ausgelegt werden. -- Wruedt 08:10, 23. Mär. 2011 (CET)
- Bezüglich der Relativität der Winkelgeschwindigkeit sind wir uns ja schonmal einig. Zum zweiten Punkt: Nehmen wir der Einfachheit halber an, dass das Lineal zwei- oder dreidimensional sei. Dann ja: Das Lineal bewegt sich nur translatorisch und hat keine Rotation. Aber die Frage war nicht, ob es eine Rotation besitzt sondern ob es eine Winkelgeschwindigkeit besitzt. Ich dachte, aus unseren früheren Gesprächen wäre klar geworden, dass die Rotationsgeschwindigkeit nur ein Spezialfall der Winkelgeschwindigkeit ist. Zu jeder Rotation gehört auch eine Winkelgeschwindigkeit. Aber nicht zu jeder Winkelgeschwindigkeit gehört eine Rotation. Unser Lineal bewegt sich zum Beispiel rein translativ auf einer Kreisbahn. Da es sich um eine Kreisbahn handelt, kann ich also einen Winkeln angeben und damit auch eine Änderung des Winkels. Und die Änderungsrate des Winkels ist nunmal eine Winkelgeschwindigkeit. Diese Winkelgeschwindigkeit hat nichts mit der Rotation zu tun. (Die Rotation ist Null.) Aber es ist dennoch eine Winkelgeschwindigkeit.
- Wenn du sachlich argumentierst und nicht persönlich wirst, kannst du den Satz von mir gerne bewerten, ohne dass es dir jemand negativ auslegt. Und ich habe bereits in aller Ruhe über diesen Satz nachgedacht. Hast du das auch? --Eulenspiegel1 00:27, 24. Mär. 2011 (CET)
- Über Deinen Satz: "Das körperfeste System dort hat eine Winkelgeschwindigkeit von Null. Aber der Körper selber hat eine Winkelgeschwindigkeit von ω. Das zeigt, dass ein starrer Körper und sein körperfestes System nicht zwangsläufig die gleiche Winkelgeschwindigkeit haben müssen." solltest Du in aller Ruhe nachdenken. Ich verkneif mir eine Wertung, denn das könnte negativ ausgelegt werden. -- Wruedt 08:10, 23. Mär. 2011 (CET)
Eine kurze Frage: Resultiert aus diesem Abschnitt, dass die Divergenz der Winkelgeschwindigkeit für rotierende Bezugssysteme gleich 0 ist, also ? Chrostiph (Diskussion) 15:15, 29. Nov. 2012 (CET)
- In dem Abschnitt wird der Sachverhalt beschrieben, dass die Winkelgeschwindigkeit eines starren Körpers in jedem Punkt des Körpers die selbe ist, sprich unabhängig vom Meßort ist.--Wruedt (Diskussion) 07:13, 30. Nov. 2012 (CET)
- Vielen Dank. Die Frage ist, ob daraus folgt, dass für rotierende Bezugssysteme mit konstanter Winkelgeschwindigkeit die Divergenz der Winkelgeschwindigkeit verschwindet. Ich wollte noch einen kurzen Satz dazuschreiben und vorher sicher gehen, dass das so stimmt. Chrostiph (Diskussion) 18:17, 4. Dez. 2012 (CET)
Einheit 1
[Quelltext bearbeiten]Zwei Bemerkungen zur Einheit:
1. rad ist keine SI-Einheit, sondern eine abgeleitete SI-Einheit mit besonderem Namen.
2. gibt es einen Grund, dass für die Winkeleinheit rad und nicht sr verwendet wird? Oder gibt es da fundamentale Unterschiede?--Brusel 13:15, 28. Mär. 2011 (CEST)
- Ja, sr bezeichnet den Raumwinkel, rad der ebene Winkel - und es gibt keinen Grund, das Problem komplizierter zu machen, die Drehbewegung findet in aller Regel ja in einer Ebene statt. Kein Einstein 15:40, 27. Feb. 2012 (CET)
Einheit 2
[Quelltext bearbeiten]Bei Rotationen werden oft auch andere Einheiten verwendet, z.B. "Umdrehungen pro Minute" (U/min) oder (da "Umdrehungen" ein einheitenloser Skalar ist) auch [1/min]. Auch sieht man durchaus Angaben in [Hz] oder [1/s] statt [rad/s]. Ich finde, das sollte (vielleicht im Abschnitt "Anwendungen und Beispiele") erwähnt werden. Physikern mag's ein Grauß sein, aber enzyklopädisch ist es nunmal eine stattfindende und imho daher zu berichtende Gegebenheit... --arilou 09:35, 27. Feb. 2012 (CET)
Nachdem Drehgeschwindigkeit und Rotationsgeschwindigkeit hierher verlinken, stimme ich dir zu. Nicht oben in der Einleitung, aber im Prinzip: Ja. Kein Einstein 15:40, 27. Feb. 2012 (CET)
- Etwas versteckt bei Anwendungen und Beispielen gibt es schon eine Verlinkung auf Drehzahl. Dort wird genau dieses Einheitenthema schon bis zur DIN vorgekaut. Vielleicht sollte man diesen Link lediglich etwas prominenter herausstellen, so mit Hauptartikel-Vorlage und so. --PeterFrankfurt 02:15, 28. Feb. 2012 (CET)
Jetzige Variante ist schon mal deutlich besser, danke Kein Einstein ! So hat man eine reele Chance, darüber zu stolpern, dass OmA bei Rotationen auch was anderes als rad/s über den Weg laufen kann. --arilou 17:52, 28. Feb. 2012 (CET)
Formelsatz
[Quelltext bearbeiten]f wird für Frequenz verwendet. Für die Kreisfrequenz ist omega gebräuchlich. Das sollte in WP einigermassen einheitlich sein. -- Wruedt 18:51, 28. Mär. 2011 (CEST)
- In diesem Artikel hier sehe ich keine Abweichung davon. An anderen Stellen ist es aber durchaus so, dass ν (nü) (E=h*ν) eher für Frequenz geschrieben wird. Konvention halt, Vereinheitlichung wäre da kontraproduktiv. --PeterFrankfurt 01:41, 29. Mär. 2011 (CEST)
- Bei Formelzeichen gibt es keine völlige Übereinstimmung in der Literatur. nü und f werden für die Frequenz am häufigsten verwendet. Hab nur eine Änderung revertiert, bei der f als Zeichen für omega verwendet wurde. Nachdem man sich bekanntlich für 1 Zeichen entscheiden muss, wurde f für Frequenz gewählt, da auch in vielen anderen WP-Artikeln und in der Literatur so. -- Wruedt 08:26, 29. Mär. 2011 (CEST)
Edit [3]
[Quelltext bearbeiten]- Eine Phase ist auch ein Winkel. Die Unterscheidung beider größeren liegt nicht dort. Eine Phase ist ein geometrischer Winkel in der komplexen Ebene.
- Wruedt: Du schreibst: „Die Winkelgeschwindigkeit gibt die Änderungsrate eines geometrischen Winkels an. Die Kreisfrequenz dagegen beschreibt die Änderung des Phasenwinkels im Kontext von Schwingungen”. Ich kann dir 1001-Quelle zeigen, bei der die Änderungsrate des Winkels des Zeigers auf dem Einheitskreis als Winkelgeschwindigkeit bezeichnet wird. Daher ist solch eine Exkluvisierung der Kreisfrequenz für Zeiger einfach falsch. Außerdem: Zeige mir eine Quelle, in der die Kreisfrequenz so 'definiert wird und nicht nur so mit der Winkelgeschw. identifiziert wird. Zusätzlich fehlt mir eine Quelle die die Allgemeinheit „Änderung des Phasenwinkels im Kontext von Schwingungen“ zeigt, also das im Artikel nicht konstante Änderungsrate stehen muss.
- Das Wesen der Kreisfrequenz ist Frequenz mit 2*pi multipliziert. Nicht mehr! Das streichst du ständig raus.--Svebert (Diskussion) 08:45, 16. Feb. 2013 (CET)
- Zu 3. +1. Diese Seelenverwandtschaft der Kreisfrequenz zur Frequenz erschließt sich mir in dem beanstandeten Satz nicht. Ansonsten empfehle ich diese (unselige) Disk. ausdrücklich nicht. IÜ wenn es eine momentane Frequenz gibt, dann gibt es auch eine momentane Kreisfrequenz. Siehe hierzu den Artikel Frequenzmodulation. Die Winkelgeschw. des Zeigers ist eine Analogie und keinesfalls ein Synonym, wie im Artikel entgegen der Quellenlage behauptet wird. Bei einer kreisförmigen Bewegung spricht man von Winkelgeschwindigkeit, bei der periodischen Änderung des Wechselstrom oder des Wasserstands von Kreisfrequenz.--Wruedt (Diskussion) 10:48, 16. Feb. 2013 (CET)
- Ich weiß das die Disk unselig ist :P
- Wikipedia-Artikel selbst zählen nicht als Quellen, zusätzlich hat ein frequenzmoduliertes Signal nicht „eine“ Kreisfrequenz. Vielmehr wird das Spektrum durch die Modulation in die breite gespreizt und das Maximum des Spetrums zeitlich verschoben. Das ist was anderes als . Bei der Frequenzmodulation musst du ins Zeigerdiagramm so viele Zeiger wie du Fourierkomponenten hast reinmalen und jede Fourierkomponente hat eine konstante Winkelgeschwindigkeit. Allein die Gewichtung bei der Zusammenmischung der Zeiger macht die Modulation aus, es wird keinesfalls ein Zeiger „abgebremst“ oder „beschleunigt“.
- DU: „Die Winkelgeschw. des Zeigers ist eine Analogie und keinesfalls ein Synonym, wie im Artikel entgegen der Quellenlage behauptet wird“. In der Quelle wird von einem Symbol geredet und „Winkelgeschwindigkeit oder Kreisfrequenz“ genannt. Sowas ist ein Synonym.
- Warum du (bzw. jetzt ist's Pewa) ständig löscht ist mir ein Rätsel. Wie gesagt: Gib mir ne Quelle für deine momentane Kreisfrequenz!--Svebert (Diskussion) 11:21, 16. Feb. 2013 (CET)
- In welcher Quelle wird das synonym verwendet und falls ja, ist diese Quelle reputabel. Auf dieses Merkmal wird von Physikern sonst bei passender Gelegenheit gepocht. Die Winkelgeschwindigkeit eines Karussells wird jedenfalls nicht mit Kreisfrequenz bezeichnet, ebensowenig die Winkelgeschwindigkeit bzw. Drehgeschwindigkeit des Mondes). IÜ verwechselst du die Fourieranalyse mit der momentanen Frequenz (zu einem bestimmten Zeitpunkt).--Wruedt (Diskussion) 13:16, 16. Feb. 2013 (CET)
- In dieser reputablen Quelle (die direkt an dem Satz im Artikel hängt) wird Winkelgeschwindigkeit und Kreisfrequenz in austauschbarer Weise verwendet. Dies habe ich als „gelegentlich synonym verwendet“ ausformuliert. Dahinter ist die 2. Quelle in der die beiden Begriffe auch in austauschbarer Weise verwendet werden.
- „Frequenzspektrum vs. momentane Kreisfrequenz“: Ich verwechsle diese beiden Begriffe gerade nicht. Warum hast du nicht diese Quelle angeführt? -> Offensichtlich ist mein Standpunkt nicht gerechtfertigt und der Begriff „Momentane Kreisfrequenz“ wird tatsächlich verwendet.--Svebert (Diskussion) 13:33, 16. Feb. 2013 (CET)
- Danke für die Klarstellung, besser fürs Klima als reflexartige reverts ohne fachlichen Hintergrund mit dem Kommentar "keine Verbesserung"--Wruedt (Diskussion) 13:31, 17. Feb. 2013 (CET)
- Mit „Keine Verbesserung“ meintest du nicht mich, oder? ([4]) ich nutze diese Floskel nie. Auch versuche ich Reverts auf ein absolutes Minimum zu halten--Svebert (Diskussion) 14:03, 17. Feb. 2013 (CET)
- Entschuldige, Du warst nicht gemeint. Aber andere Physiker nutzen gern dieses Instrument, ohne dass der fachliche Hintergrund immer erkennbar ist.--Wruedt (Diskussion) 17:26, 18. Feb. 2013 (CET)
- Mit „Keine Verbesserung“ meintest du nicht mich, oder? ([4]) ich nutze diese Floskel nie. Auch versuche ich Reverts auf ein absolutes Minimum zu halten--Svebert (Diskussion) 14:03, 17. Feb. 2013 (CET)
- Danke für die Klarstellung, besser fürs Klima als reflexartige reverts ohne fachlichen Hintergrund mit dem Kommentar "keine Verbesserung"--Wruedt (Diskussion) 13:31, 17. Feb. 2013 (CET)
- In welcher Quelle wird das synonym verwendet und falls ja, ist diese Quelle reputabel. Auf dieses Merkmal wird von Physikern sonst bei passender Gelegenheit gepocht. Die Winkelgeschwindigkeit eines Karussells wird jedenfalls nicht mit Kreisfrequenz bezeichnet, ebensowenig die Winkelgeschwindigkeit bzw. Drehgeschwindigkeit des Mondes). IÜ verwechselst du die Fourieranalyse mit der momentanen Frequenz (zu einem bestimmten Zeitpunkt).--Wruedt (Diskussion) 13:16, 16. Feb. 2013 (CET)
Einheit für Zentripetalkraft
[Quelltext bearbeiten]Hier im Artikel wird gesagt das die Einheit rad/s ist. Bei Zentripetalkraft steht auch a=w²×r welches dann die Einheit rad²×m/s ergeben würde. Irgendwie erscheint mir das seltsam, weil wer sagt das die Winkelgeschwindigkeit nicht 1/s ist? Dadurch würde der rad² Term wegfallen. Oder kann man den einfach ignorieren? — xZise [disk] 12:05, 25. Apr. 2013 (CEST)
- Bitte SI-Einheit#Abgeleitete SI-Einheiten mit besonderem Namen lesen; dort:
- [rad] = [m/m] = [1]
- D.h. die Einheit "rad" kann auch einfach weggelassen werden. Sie dient i.A. dazu, (nochmals) zu verdeutlichen, dass Winkelrechnungen im Bogenmaß gegeben sind, und nicht im Gradmaß.
- --arilou (Diskussion) 13:38, 25. Apr. 2013 (CEST)
- Okay danke. Wolfram Alpha hatte mich da ein bisschen verunsichert. — xZise [disk] 15:37, 27. Apr. 2013 (CEST)
Abgrenzung zur Kreisfrequenz
[Quelltext bearbeiten]Die Quellen geben eine synonyme Verwendung von Winkelgeschw. und Kreisfreq. nicht her. Vielmehr ist von ANALOGIE die Rede. Das gleiche Formelzeichen ist kein Beweis für eine synonyme Verwendung. Der Abschnitt grenzt an TF und sollte imo entweder gelöscht oder deutlich präzisiert werden. Winkelgeschwindigkeit wird bei Bohrmaschinen, Karussel's, Generatoren, etc verwendet, Kreisfrequenz im Kontext von Schwingungen. Z.B. der Generator erzeugt beí einer gegebenen Winkelgeschwindigkeit an seinen Klemmen einen Wechselstrom entsprechender Kreisfrequenz.--Wruedt (Diskussion) 16:53, 27. Apr. 2013 (CEST)
- Wo ist Dein Problem? Der Abschnitt heißt Abgrenzung zur Kreisfrequenz. Er steht genau aus einem Grund da: Um der Verwechslung der beiden Größen entgegenzuwirken. Wortwörtlich steht da: Sie [die Kreisfrequenz] ist also – wie auch die Frequenz – ein Maß dafür, wie schnell eine Schwingung abläuft und hat ansonsten nichts mit einer Rotation im eigentlichen Sinne zu tun. --Pyrrhocorax (Diskussion) 17:29, 27. Apr. 2013 (CEST)
- Das ist imo ein klarer Fall von Quellenmißbrauch. Die erste Quelle spricht von Analogie, die 2. Quelle stellt klar, dass Winkelgeschw. bei Rotationen und Kreisfrequenz in der Schwingungslehre verwendet wird. Werde den Abschnitt wegen TF löschen. In Kreisfrequenz wird auf die Analogie eingegangen, die darin besteht, dass die Kreisfrequenz über den besagten Zeiger in der komplexen Ebene veranschaulicht wird. Von einer synonymen Verwendung kann in ernsthaften Quellen nicht die Rede sein. Eine "Verwechslung" der beiden Begriffe wird hier erst herbeigeredet ==> TF--Wruedt (Diskussion) 22:49, 27. Apr. 2013 (CEST)
- Okay, war wohl ein Missverständnis. Den ersten (nun gelöschten) Satz fand ich auch schon immer unglücklich und er entstand aus einer Diskussion bei der QS Physik bei der manche Nutzer (weiß nicht mehr welche) behaupteten, dass die beiden Begriffe synonym verwendet würden. Das ging sogar soweit, dass gefordert wurde, beide Artikel zu einem Artikel zu verschmelzen. Ich dachte, Du wolltest den gesamten Abschnitt "Abgrenzung..." löschen, und das wäre natürlich falsch, denn eine Verwechslung der beiden Begriffe (aus Schusseligkeit oder Unwissenheit) kommt schon sehr häufig vor, weshalb eine Abgrenzung wichtig ist. Ich habe Deine Formulierung noch um einen einleitenden und abschließenden Satz ergänzt, damit der Leser weiß, warum dieser Abschnitt überhaupt in dem Artikel steht. --Pyrrhocorax (Diskussion) 10:39, 28. Apr. 2013 (CEST)
- @Pyrrhocorax: Eine Schwingung kann mathematisch durch einen rotierenden Zeiger dargestellt werden, muss aber nicht. Wenn die Schwingung durch einen rotierenden Zeiger dargestellt wird, dann ist dieser Zeiger definitionsgemäß immer komplex und rotiert in der komplexen Ebene. -- Pewa (Diskussion) 19:09, 28. Apr. 2013 (CEST) PS: Ohne den komplexen Zeiger rotiert bei einer Schwingung gar nichts. -- Pewa (Diskussion) 19:19, 28. Apr. 2013 (CEST)
- Nein. Ein Zeiger kann auch im rotieren. Er ist ja sowieso nur ein gedankliches Konstrukt. Ob man ihn in der komplexen Ebene oder im zweidimensionalen reellen Raum definiert, bleibt demjenigen überlassen, der ihn definiert. Zwar ist es zweckmäßig den Zeiger in der komplexen Ebene rotieren zu lassen, weil man dann die dortige Verwandtschaft der trigonometrischen Funktionen mit der e-Funktion nutzen kann. Das ist aber nicht notwendig. In der gymnasialen Oberstufe wird beispielsweise ein rein reelles Zeigermodell verwendet, weil die Schüler keine Kenntnis von komplexen Zahlen haben. Das ist dann nicht falsch, sondern nur anders. Insbesondere braucht man in diesem Artikel (Winkelgeschwindigkeit!) auf diese Feinheiten gar nicht einzugehen. Ohne das Wort "komplex" wird der Abschnitt erheblich lesbarer. Übrigens - ganz nebenbei - die komplexe Zahlenebene ist die räumliche Veranschaulichung des Körpers der komplexen Zahlen. Die Geometrie dieser Ebene ist keineswegs komplex. Sie wurde genau so konstruiert, um die komplexen Zahlen sozusagen mit "reellen" Mitteln darstellen zu können, denn die Koordinaten der komplexen Zahl z (sowohl Re(z) als auch Im(z)) sind reelle Zahlen. Somit ist die komplexe Zahlenebene von der Geometrie her ebenfalls ein und unterscheidet sich nur durch die Beschriftung der Koordinatenachsen.--Pyrrhocorax (Diskussion) 19:49, 28. Apr. 2013 (CEST)
- Das ist falsch. Wenn etwas in rotiert ist es ein Vektor und kein Zeiger. Wenn man den Schülern wirklich verschweigt, dass Zeiger mathematisch komplexe Größen sind, sollte man ihnen besser gar nichts über Zeiger erzählen, statt solchen irreführenden Unsinn, der es ihnen wahrscheinlich unmöglich macht zu verstehen was Zeiger wirklich sind. Au0erdem darf deine Behauptung bezweifelt werden, siehe Zeigermodell im Physikunterricht der Kursstufe. Außerdem wären verfehlte Lehrpläne von Schulen kein Grund für falsche Darstellungen in Wikipedia. Wikipedia stellt das etablierte Wissen dar und keine irreführend reduzierte "Kinderversion".
- Alle Berechnungen mit Zeigern funktionieren nur, weil Zeiger komplexe Größen sind. Man kann mit Zeigern rechnen und man kann sie in der komplexen Ebene veranschaulichen, weil sie komplexe Größen sind. Zeiger sind niemals Vektoren in .
- Hör auf mit deinem Versuch das etablierte Wissen in Wikipedia auf eine verfehlte "Kinderversion" zu reduzieren. -- Pewa (Diskussion) 21:29, 28. Apr. 2013 (CEST)
- Ich habe mir deinen Link durchgelesen und ich habe dort nichts gefunden, was gegen Zeiger im spricht. Und natürlich kann man Zeigeroperationen in (also hauptsächlich Drehung und Verlängerung) auch problemlos in durchführen. --Eulenspiegel1 (Diskussion) 23:05, 28. Apr. 2013 (CEST)
- @Pewa. Erstens: Natürlich sind Zeiger Vektoren, und zwar egal ob man sie komplex darstellt oder reell. Komplexe Zahlen sind nämlich auch Vektoren. Zweitens: Die komplexe Zahlenebene ist von ihrer Struktur her nicht vom zu unterscheiden. Es handelt sich bei ihr um ein 2-dimensionales kartesisches Koordinatensystem. Deshalb sind alle Beziehungen, die es in gibt, automatisch auch im darstellbar und umgekehrt. Die einzige Besonderheit der komplexen Zahlen ist die imaginäre Einheit . Aber das ist keine Eigenschaft der komplexen Ebene sondern der komplexen Zahlen. Für die Darstellung von Schwingungen ist diese Besonderheit irrelevant, da die Momentanauslenkung einer Schwingung immer (je nach Definition) der Realteil oder der Imaginärteil, also eine reelle Zahl ist. Drittens: Herr Philipp schreibt in dem von Dir verlinkten Papier ja gerade, dass Zeiger statt komplexer Zahlen verwendet werden sollen. (Nur am Rande: Ich kenne ihn flüchtig und Freunde von mir hatten bei ihm Physik-LK). Viertens: Bevor Du über "verfehlte Lehrpläne" polterst, stünde es Dir gut an, mal über den Sinn und Zweck von didaktischer Reduktion nachzudenken. Das hat nichts mit Verschweigen zu tun, sondern mit altersgerechtem Unterrichten. --Pyrrhocorax (Diskussion) 00:35, 29. Apr. 2013 (CEST)
- Du solltest die Einleitung "4 Mathematische Bedeutung von Zeigern" lesen und verstehen. Im Gegensatz zu dir versucht er nicht zu verschweigen, dass Zeiger komplexe Zahlen repräsentieren. Allerdings verwendet er den Begriff "Zeiger" nur in einer eingeschränkten Bedeutung als graphische Darstellung einer komplexen Zahl durch einen Pfeil in einer Ebene. In dieser Darstellung von komplexen Zahlen kann man die Pfeile auch geometrisch addieren oder drehen, was er ebenfalls beschreibt. Das ist aber weniger als die halbe Wahrheit, denn mathematisch ist ein "Zeiger" einfach eine komplexe Größe, unabhängig von irgend einer graphischen Darstellung. Man kann mit Zeigern rechnen ohne dafür eine graphische Darstellung zu benötigen. Man kann Zeiger auch multiplizieren und dividieren, was graphisch nicht darstellbar ist. Für alle Berechnungen mit Zeigern gelten die Rechenregeln für komplexe Zahlen und nicht etwa die Rechenregeln für Vektoren in . Zeiger und allgemein komplexe Zahlen bilden den Vektorraum und sind keine Vektoren in . Siehe auch Abschnitt 4.5: "Betrachtet man dagegen in einem Zeigerdiagramm einen rotierenden Zeiger der Länge U, so steht dieser Zeiger im Zusammenhang mit einer komplexen Zahl."
- Wikipedia stellt das etablierte Wissen dar und ist kein Schulbuch für "altersgerechtes Unterrichten". Wer nicht gelernt hat mit komplexen Zahlen zu rechnen kann auch nicht mit Zeigern rechnen und wird vermutlich Probleme damit haben zu verstehen was Zeiger sind und warum man sie verwendet. Das ist bedauerlich aber nicht zu ändern, sonst müsste man große Teile von Wikipedia löschen.
- Du kannst auch nicht erklären welche physikalische Bedeutung der Phasenwinkel der Spannung in haben soll, weil er dort keine physikalische Bedeutung hat. -- Pewa (Diskussion) 10:19, 29. Apr. 2013 (CEST)
- Nein. Ein Zeiger kann auch im rotieren. Er ist ja sowieso nur ein gedankliches Konstrukt. Ob man ihn in der komplexen Ebene oder im zweidimensionalen reellen Raum definiert, bleibt demjenigen überlassen, der ihn definiert. Zwar ist es zweckmäßig den Zeiger in der komplexen Ebene rotieren zu lassen, weil man dann die dortige Verwandtschaft der trigonometrischen Funktionen mit der e-Funktion nutzen kann. Das ist aber nicht notwendig. In der gymnasialen Oberstufe wird beispielsweise ein rein reelles Zeigermodell verwendet, weil die Schüler keine Kenntnis von komplexen Zahlen haben. Das ist dann nicht falsch, sondern nur anders. Insbesondere braucht man in diesem Artikel (Winkelgeschwindigkeit!) auf diese Feinheiten gar nicht einzugehen. Ohne das Wort "komplex" wird der Abschnitt erheblich lesbarer. Übrigens - ganz nebenbei - die komplexe Zahlenebene ist die räumliche Veranschaulichung des Körpers der komplexen Zahlen. Die Geometrie dieser Ebene ist keineswegs komplex. Sie wurde genau so konstruiert, um die komplexen Zahlen sozusagen mit "reellen" Mitteln darstellen zu können, denn die Koordinaten der komplexen Zahl z (sowohl Re(z) als auch Im(z)) sind reelle Zahlen. Somit ist die komplexe Zahlenebene von der Geometrie her ebenfalls ein und unterscheidet sich nur durch die Beschriftung der Koordinatenachsen.--Pyrrhocorax (Diskussion) 19:49, 28. Apr. 2013 (CEST)
- Zuerst zum letzten Punkt: Natürlich kann ich das erklären: Der Phasenwinkel ist der Winkel, um den die Zeiger von Spannung und Stromstärke gegeneinander verschoben sind. Dafür brauche ich keine komplexen Zahlen.
- Nun zum Thema etabliertes Wissen: Es ist etabliertes Wissen, dass sich periodische Vorgänge durch einen rotierenden Zeiger darstellen lässt. Dass dieser Zeiger komplexwertig ist, ist eine Konvention, die sich als nützlich erwiesen hat, aber es ist nichtsdestotrotz eine Konvention, der man nicht folgen muss. Die Verwendung von komplexen Zahlen für periodische Vorgänge ist nicht allein durch Versuchsergebnisse zu rechtfertigen. (Wie auch? Wie soll denn ein Spannungsmessgerät eine "imaginäre Spannung" anzeigen können). Abgesehen davon hat die Wikipedia nicht nur den Anspruch, etabliertes Wissen darzustellen, sondern es auch verständlich darzustellen. Viele derer, die sich mit den Begriffen Winkelgeschwindigkeit und Kreisfrequenz herumschlagen (ja, auch Schüler!) erwarten von der Wikipedia eine verständlich Abgrenzung der Begriffe. Und da der Begriff der komplexen Zahl hier überhaupt nicht notwendig ist, dient er lediglich dazu, dem unwissenden Leser seine Unwissenheit aufs Brot zu schmieren. Schließlich zum Paper von Philipp: Natürlich tauchen im Einleitungskapitel komplexe Zahlen auf, denn der Artikel ist ja nicht für Schüler geschrieben sondern für Physik-Lehrer, die aus dem Studium (hoffentlich) wissen, was es mit den komplexen Zeigern auf sich hat. Nach diesem Einleitungsabschnitt taucht aber keine einzige komplexe Zahl mehr in dem Artikel auf, was ein eindeutiger Beleg dafür ist, dass Zeiger keineswegs komplexwertig sein müssen oder - noch schlimmer - sind (wie Du weiter oben schreibst). Zeiger sind gedankliche Konstrukte und erhalten ihre Eigenschaften nur durch ihre Definition. Es gibt in der Natur keine Zeiger.--Pyrrhocorax (Diskussion) 12:35, 29. Apr. 2013 (CEST)
- Du verstehst einfach nicht, dass ein Pfeil auf einem Blatt Papier nur eine symbolische Darstellung eines komplexen Zeigers ist, aber keine komplexe Größe. Du musst erklären wo du das Geo-Dreieck an die Spannung und den Strom an der Impedanz anlegst, um einen ebenen Winkel zwischen Spannung und Strom in zu messen. Das kannst du nicht. Der Phasenwinkel in hat eine gänzlich andere physikalische Bedeutung als ein ebener Winkel in . Deine Behauptung, dass es keinen Unterschied zwischen den Vektorräumen und gibt ist einfach nur Unsinn. -- Pewa (Diskussion) 14:04, 29. Apr. 2013 (CEST)
- In Naturwissenschaft und Technik sind Zeiger als komplexe Größen definiert für die die Rechenregeln für komplexe Zahlen gelten. Wenn an Schulen etwas anderes gelehrt wird, weil man meint, den Schülern nicht die ganze Wahrheit zumuten zu können, ist das ein Problem für die Schüler und die Schulen. Es ist nicht die Aufgabe der Wikipedia den Schülern etwas falsches zu bestätigen, weil sie es in der Schule falsch gelernt haben. Hier ist alleine die physikalische und technische Fachliteratur maßgeblich. Wenn die Lehrer es den Schülern wirklich verschweigen, dass es sich bei Zeigern um komplexe Größen handelt, damit die Schüler nicht merken sollen, dass ihnen noch weitergehende Kenntnisse und Fähigkeiten fehlen, um Berechnungen mit Zeiger richtig verstehen zu können, halte ich das für ein geradezu tragisches Versäumnis das den Schülern übel mitspielt, weil es den Schülern ein späteres richtiges Verständnis von Zeigern fast unmöglich macht. Es gibt keinen vernünftigen Grund dafür durch deine Löschungen von Fakten und Zusammenhängen, Wikipedia zum Komplizen dieses üblen Spiels zu machen. Wenn du willst, kannst du aber gerne ein separates Kapitel über die Behandlung von Zeigern in der Schule schreiben. -- Pewa (Diskussion) 14:40, 29. Apr. 2013 (CEST)
Mein lieber Scholli, da ist aber jemand wirklich in Fahrt! Es geht hier um die Frage, warum die Winkelgeschwindigkeit nicht dasselbe ist, wie die Kreisfrequenz. So. Bitteschön wofür muss ich nun wissen, ob der Zeiger komplex oder reell ist? Schon allein deshalb ist es unnötig zu erwähnen, dass der Zeiger in der komplexen Ebene rotiert. Das wäre schon Argument genug, um diese Phrase aus dem Artikel draußen zu lassen, ganz unabhängig von der Frage der sachlichen Richtigkeit. Nun zu dieser: Ein Zeiger beschreibt Schwingungen. Warum tut er das? Weil die Schwingung kosinusförmig ist und weil im Einheitskreis gilt . Was ist daran bitteschön komplex? Nichts! Auch die Lösung der Differenzialgleichung des harmonischen Oszillator verlangt nicht nach einer komplexen Größe, denn statt kann man jederzeit auch den Sinus oder den Kosinus nehmen, ohne irgendwas an Information zu verlieren. Ein reelles Zeigermodell ist also vom Informationsgehalt absolut gleichwertig mit einem komplexen Zeigermodell. Das komplexe Zeigermodell wird in der Uni-Physik bevorzugt, weil es die Rechnung z. B. in der Wechselstromlehre vereinfacht. Die unbestrittene Verwendung des komplexen Zeigermodells in der Uni-Physik ist aber kein Grund anzunehmen, dass das reelle Zeigermodell nicht zum Einsatz kommt (mindestens in der Schule wird es verwendet). Und erst recht ist es kein Beleg dafür, dass das reelle Zeigermodell falsch wäre. Es kann nämlich gar nicht falsch sein, weil die komplexe Zahlenebene dieselbe Geometrie hat wie der (ein Argument, das Du beharrlich überhörst). Du fühlst Dich berufen zu urteilen, dass ein angebliches Versäumnis der Schule es den Schülern fast unmöglich mache, das Zeigermodell richtig zu verstehen. Andererseits kannst Du nicht nachvollziehen, dass ein reelles Zeigermodell vom Informationsgehalt genau gleich ist wie ein komplexes Zeigermodell und Du behauptest, dass es „Fakten“ seien, was ich gelöscht hätte. (Du weißt aber schon, was ein Modell ist?). Das bringt mich zu dem Schluss, dass die Verständnisschwierigkeiten nicht auf der Seite der Schule liegen, sondern auf Deiner Seite. Schönen Tag noch! --Pyrrhocorax (Diskussion) 16:33, 29. Apr. 2013 (CEST)
- +1 Pyrrhocorax: Der Unterschied ist, dass ein Körper ist, da schon ein Skalarprodukt definiert ist, während zunächst nur eine Gruppe ist. Man kann die Gruppe aber einfach zum Körper machen, also mit euklidischem Skalarprodukt. Dann sind beide Räume isomorph und somit ist es egal, ob man komplexe Zahlen nimmt oder nicht. Der Vorteil komplexer Zahlen ist lediglich die einfachere Notation, also zum Beispiel statt , dank komplex definierter Exponentialfunktion. Außerdem muss man nicht dazusagen, dass man euklidische Koordinaten benutzt.
- Ansonsten: Ich habe bei der Diskussion in der Physik-QS schon gesagt, dass das Problem Frequenz-Kreisfrequenz-Winkelgeschwindigkeit nicht gelöst ist und es daher immer wieder kommen wird, solange im ersten Absatz keine vernünftige abgrenzende Definition steht. Ich finde es außerdem nicht gut, dass der Satz zur Synonymen Verwendung gelöscht wurde. Es existiert keine klare Definition für eine Kreisfrequenz (siehe Endlosdiskussion) und das sollte Wikipedia dann auch wiederspiegeln. Es gibt nunmal einen Unterschied zwischen
- , also eine Konvention zur Angabe einer Frequenz im Bogenmaß (Ansicht Pyrrhocorax)
- , also die Winkelgeschwindigkeit des Phasenwinkels (Ansicht Pewa)
- Beides liefert auch andere Werte, wenn man sich nicht nur auf Sinusschwingungen beschränkt, wie es der Artikel Kreisfrequenz es tut.--Debenben (Diskussion) 18:56, 29. Apr. 2013 (CEST)
- Was du hier unterstellst ist leider auch wieder falsch.
- ist die Kreisfrequenz einer harmonischen Schwingung. Die Kreisfrequenz ist die Änderungsgeschwindigkeit des Phasenwinkels in der komplexen Ebene.
- ist die harmonische Schwingung in der komplexen Ebene.
- Nicht-harmonische Schwingungen kann man allgemein nicht durch eine einzelne Kreisfrequenz beschreiben, sondern nur durch eine Summe von harmonischen Schwingungen mit unterschiedlichen Kreisfrequenzen. -- Pewa (Diskussion) 20:35, 29. Apr. 2013 (CEST)
- Was du hier unterstellst ist leider auch wieder falsch.
- @Pyrrhocorax: Man, man, man, ja es stimmt dass du nicht wissen musst, was ein Zeiger ist, ob ein Zeiger komplex ist und wodurch er sich von einem Vektor unterscheidet. Du hast ein Recht auf Nichtwissen. Andere haben ein Recht, das zu wissen, was man in Naturwissenschaft und Technik unter einem Zeiger versteht. Wenn du es nicht wissen willst was einen rotierenden Vektor von einem rotierenden Zeiger unterscheidet, solltest du auch nicht versuchen das zu erklären oder die Erklärung hier zu löschen. Du wirst dieses Wissen hier nicht unterdrücken, weil es deiner Theoriefindung widerspricht. Du hast offenbar keine Ahnung warum man Zeiger verwendet und wie man mit Zeigern rechnet. Es gibt kein "reelles Zeigermodell", wenn Schüler das wirklich in der Schule lernen müssen, dann lernen sie das nur für die Schule. Das ist zum Glück nicht mein Problem und nicht das Problem von Wikipedia. Wenn in der Schule wirklich ein "reelles Zeigermodell" gelehrt wird und du das durch Quellen belegen kannst, solltest den Artikel "Das reelle Zeigermodell für die Schule" schreiben.
- PS: Erklär doch mal, wie du die Spannung mit deinem "reellen Zeigermodell" berechnest. -- Pewa (Diskussion) 20:01, 29. Apr. 2013 (CEST)
- Ja, der Leser sollte erfahren, was ein Zeiger ist. Aber bitte nicht in diesem Artikel sondern in einem Artikel über Zeiger. In diesem Artikel hier geht es um Winkelgeschwindigkeiten.
- Und bei der Berechnung der Spannung kommt es darauf an, welche Apparatur du verwendest: Hast du Gleichstrom, sinusförmigen Wechselstrom, Wechselstrom mit Sägezahnspannung, anderen Wechselstrom, Kondensatoren etc.? Was für Widerstände benutzt du: Ohmsche Widerstände oder induktive Widerstände? Zeige mir die schematische Zeichnung der Apparatur und ich kann dir sagen, wie man dort die Spannung berechnet. --Eulenspiegel1 (Diskussion) 20:52, 29. Apr. 2013 (CEST)
- Ich weiß wie man die Spannung mit Zeigern berechnet. Ich will wissen, wie Pyrrhocorax sie mit seinem "reellen Zeigermodell" berechnen will, und zwar nicht nur das Ergebnis, sondern auch den Rechenweg. Zum Beispiel mit dem Strom: und . -- Pewa (Diskussion) 21:22, 29. Apr. 2013 (CEST)
- Wohl eher: und --Eulenspiegel1 (Diskussion) 21:37, 29. Apr. 2013 (CEST)
- Was soll das denn werden? Du solltest wenigstens beachten, dass ein Strom und eine Impedanz ist. -- Pewa (Diskussion) 21:56, 29. Apr. 2013 (CEST)
- Das soll erklären, wie man Strom und Impedanz ohne komplexe Zahlen darstellen kann. --Eulenspiegel1 (Diskussion) 22:03, 29. Apr. 2013 (CEST)
- Du willst eine Impedanz durch eine dimensionslose reelle Zahl darstellen? Dann mal viel Spaß bei der Berechnung der Spannung. -- Pewa (Diskussion) 22:27, 29. Apr. 2013 (CEST)
- Wenn es dir um die Einheit geht, die ist . Ausgeschrieben haben wir also --Eulenspiegel1 (Diskussion) 22:53, 29. Apr. 2013 (CEST)
- Die Einheit stimmt jetzt immerhin. Die Impedanz ist aber kein reeller Widerstand und der Betrag ist auch falsch. Wenn du nicht selbst siehst, dass das immer noch Quatsch ist, gebe ich es auf. -- Pewa (Diskussion) 00:04, 30. Apr. 2013 (CEST)
- Wenn du nicht erkennst, dass es richtig ist, nachdem ich es dir haarklein hingeschrieben habe, dann gebe ich es auf. Es geht doch gerade darum, dass man alles reell darstellen kann. Rein physikalisch interessieren bei der Impedanz doch nur zwei Sachen: 1) Wie groß ist das Verhältnis Spannung zu Stromstärke. Und 2) Wie groß ist der Phasenunterschied zwischen Spannung und Stromstärke. Das sind die beiden Informationen, die von Interesse sind. Und beides sind reelle Zahlen. --Eulenspiegel1 (Diskussion) 00:27, 30. Apr. 2013 (CEST)
- Du hast es "haarklein" falsch hingeschrieben und siehst immer noch nicht, dass es falsch ist. Du siehst nicht dass die komplexe Impedanz ist und dass auf der rechten Seite nur der Wirkwiderstand steht. Wo ist der Blindwiderstand der Impedanz geblieben? Wie drückst du die vollständige komplexe Impedanz rein reell aus? .
- Niemand hat bestritten, dass man auch ohne komplexe Zahlen und Zeiger rechnen kann, wenn man es richtig macht. Es ist nur viel umständlicher. Man kann es aber nicht mit "reellen Zeigern" berechnen, weil das Quatsch ist, weil es keine "reellen Zeiger" gibt. -- Pewa (Diskussion) 01:41, 30. Apr. 2013 (CEST)
- Wenn du nicht erkennst, dass es richtig ist, nachdem ich es dir haarklein hingeschrieben habe, dann gebe ich es auf. Es geht doch gerade darum, dass man alles reell darstellen kann. Rein physikalisch interessieren bei der Impedanz doch nur zwei Sachen: 1) Wie groß ist das Verhältnis Spannung zu Stromstärke. Und 2) Wie groß ist der Phasenunterschied zwischen Spannung und Stromstärke. Das sind die beiden Informationen, die von Interesse sind. Und beides sind reelle Zahlen. --Eulenspiegel1 (Diskussion) 00:27, 30. Apr. 2013 (CEST)
- Die Einheit stimmt jetzt immerhin. Die Impedanz ist aber kein reeller Widerstand und der Betrag ist auch falsch. Wenn du nicht selbst siehst, dass das immer noch Quatsch ist, gebe ich es auf. -- Pewa (Diskussion) 00:04, 30. Apr. 2013 (CEST)
- Wenn es dir um die Einheit geht, die ist . Ausgeschrieben haben wir also --Eulenspiegel1 (Diskussion) 22:53, 29. Apr. 2013 (CEST)
- Du willst eine Impedanz durch eine dimensionslose reelle Zahl darstellen? Dann mal viel Spaß bei der Berechnung der Spannung. -- Pewa (Diskussion) 22:27, 29. Apr. 2013 (CEST)
- Das soll erklären, wie man Strom und Impedanz ohne komplexe Zahlen darstellen kann. --Eulenspiegel1 (Diskussion) 22:03, 29. Apr. 2013 (CEST)
- Was soll das denn werden? Du solltest wenigstens beachten, dass ein Strom und eine Impedanz ist. -- Pewa (Diskussion) 21:56, 29. Apr. 2013 (CEST)
- Wohl eher: und --Eulenspiegel1 (Diskussion) 21:37, 29. Apr. 2013 (CEST)
- Ich weiß wie man die Spannung mit Zeigern berechnet. Ich will wissen, wie Pyrrhocorax sie mit seinem "reellen Zeigermodell" berechnen will, und zwar nicht nur das Ergebnis, sondern auch den Rechenweg. Zum Beispiel mit dem Strom: und . -- Pewa (Diskussion) 21:22, 29. Apr. 2013 (CEST)
- Vielleicht hast du übersehen, dass es hier um den Abschnitt "Abgrenzung zur Kreisfrequenz" geht, oder willst du den Unterschied zwischen Winkelgeschwindigkeit und Kreisfrequenz erklären ohne den Unterschied zwischen Winkelgeschwindigkeit und Kreisfrequenz zu erklären? Wir können den Abschnitt auch ganz weglassen, wenn die Freunde der Winkelgeschwindigkeit es nicht zulassen wollen, dass der Unterschied hier erklärt wird. -- Pewa (Diskussion) 21:56, 29. Apr. 2013 (CEST)
- Du hattest die Zwischenfrage gestellt, wie man elektrische Größen darstellen kann, ohne komplexe Zahlen zu verwenden. Wenn wir uns mittlerweile aber einig sind, dass diese Frage nichts mit "Abgrenzung zur Kreisfrequenz" zu tun hat, können wir diesen Teilabschnitt gerne ad acta legen. --Eulenspiegel1 (Diskussion) 22:03, 29. Apr. 2013 (CEST)
- Nein, ich habe Pyrrhocorax gefragt, wie er die Spannung mit seinem "reellen Zeigermodell" berechnen will.
- Außerdem war das eine Antwort auf deine Bemerkung, dass der Leser hier nicht erfahren soll, was der Unterschied zwischen einem reellen Vektor der mit einer Winkelgeschwindigkeit rotiert und einem Zeiger der mit einer Kreisfrequenz in der komplexen Ebene rotiert ist. -- Pewa (Diskussion) 22:40, 29. Apr. 2013 (CEST)
- Zum ersten Satz: Das habe ich doch gesagt. Wieso "Nein"? Und ich habe dir darauf geantwortet.
- Ab dem zweiten Satz: Der Leser soll hier nicht erfahren, was der Unterschied zwischen einem reellen Vektor und einem komplexen Vektor ist. Der Leser soll erfahren, was der Unterschied zwischen Winkelgeschwindigkeit und Kreisfrequenz ist. Und die Antwort lautet nicht: "Das eine findet in der reellen Ebene statt und das andere findet in der komplexen Ebene statt." Die Antwort lautet stattdessen: "Das eine beschreibt eine Rotation und das andere beschreibt eine Schwingung." Wenn du einen Zeiger in der komplexen Ebene hast, der rotiert, dann hat dieser Zeiger in der komplexen Ebene eine Winkelgeschwindigkeit. Die Projektion dieser Rotation ergibt eine Schwingung. Und diese Schwingung (also die Projektion der Rotation) hat eine Kreisfrequenz. Jetzt ist es aber gerade bei harmonischen Schwingungen so, dass Winkelgeschwindigkeit des Zeigers und Kreisfrequenz der Schwingung den gleichen Wert haben. Nichtsdestrotz beschreibt die Winkelgeschwindigkeit eine Rotation und die Kreisfrequenz eine Schwingung. --Eulenspiegel1 (Diskussion) 23:58, 29. Apr. 2013 (CEST)
- 1. Nein, du hast die Frage nicht verstanden. Die Frage war nicht, wie man die Spannung ohne Zeiger berechnet, sondern wie man sie mit "reellen Zeigern" berechnet.
- 2. Da du auch nicht verstehen willst, dass ein Zeiger immer eine komplexe Größe ist, kannst du auch den Unterschied zwischen einem Vektor und einem Zeiger nicht verstehen. Dann kannst du auch nicht verstehen, dass ein Zeiger nur in der komplexen Ebene rotieren kann. Dann kannst du auch nicht verstehen, dass der Winkel in der komplexen Ebene "Phase" heißt, und dass der Zeiger eben nicht mit einer "Winkelgeschwindigkeit" rotiert, sondern mit einer "Phasengeschwindigkeit", die als Kreisfrequenz bezeichnet wird. Schwingungen werden durch einen komplexen Zeiger beschrieben, der in der komplexen Ebene mit der Kreisfrequenz rotiert. Aber wahrscheinlich ist es zwecklos, das hier immer wieder zu erklären, wenn die Grundlagen schon in der Schule falsch gelehrt werden. -- Pewa (Diskussion) 08:38, 30. Apr. 2013 (CEST)
- Du hattest die Zwischenfrage gestellt, wie man elektrische Größen darstellen kann, ohne komplexe Zahlen zu verwenden. Wenn wir uns mittlerweile aber einig sind, dass diese Frage nichts mit "Abgrenzung zur Kreisfrequenz" zu tun hat, können wir diesen Teilabschnitt gerne ad acta legen. --Eulenspiegel1 (Diskussion) 22:03, 29. Apr. 2013 (CEST)
- Vielleicht hast du übersehen, dass es hier um den Abschnitt "Abgrenzung zur Kreisfrequenz" geht, oder willst du den Unterschied zwischen Winkelgeschwindigkeit und Kreisfrequenz erklären ohne den Unterschied zwischen Winkelgeschwindigkeit und Kreisfrequenz zu erklären? Wir können den Abschnitt auch ganz weglassen, wenn die Freunde der Winkelgeschwindigkeit es nicht zulassen wollen, dass der Unterschied hier erklärt wird. -- Pewa (Diskussion) 21:56, 29. Apr. 2013 (CEST)
- @Pyrrhocorax: Du kannst keine einzige fachlich geeignete Quelle für deine TF "reelles Zeigermodell" und Berechnungen damit liefern, also hör mit dem Editwar für deine TF auf. -- Pewa (Diskussion) 21:22, 29. Apr. 2013 (CEST)
- Jetzt wird es ja ganz wirr: Wieso soll ich etwas, was ich nicht geschrieben habe, mit Quellen belegen? Ich habe nämlich im Artikel nicht geschrieben, dass der Zeiger reell sei. Tatsächlich habe ich immer wieder versucht, eine Version wiederherzustellen, die nicht darauf pocht, dass der Zeiger in der komplexen Zahlenebene dargestellt wird, sondern diese Frage offen lässt. Weil nämlich beides geht, wie inzwischen ja von Debenben und Eulenspiegel bestätigt wurde (dafür Danke). Und außerdem ist es für die Frage, warum eine Kreisfrequenz keine Winkelgeschwindigkeit ist, vollkommen wurscht, in welchem Raum sich der Zeiger tummelt. Was die Quellenlage anbetrifft: Ich könnte jedes Physikbuch der gymnasialen Oberstufe als Quelle angeben, aber Du hast ja schon weiter oben klar gemacht, dass Du diese Quellen nicht anerkennen wirst. --Pyrrhocorax (Diskussion) 22:43, 29. Apr. 2013 (CEST)
- P.S.: Die persönlichen Beleidigungen und unhaltbaren Behauptungen von weiter oben ignoriere ich noch nicht einmal. --Pyrrhocorax (Diskussion) 22:51, 29. Apr. 2013 (CEST)
- Langsam wird es wirklich absurd. Du bestehst darauf, dass ein Zeiger keine komplexe Größe sein muss und kannst es durch nichts belegen und bestehst darauf das in den Artikel zu schreiben. Ich habe mit dem Oberstufen-Script belegt, dass auch dort eindeutig erklärt wird, dass ein Zeiger eine komplexe Größe ist. Du meinst, dass der Lehrer den Schülern diese Tatsache verschweigen soll, und dass deswegen auch Wikipedia seinen Lesern diese Tatsache verschweigen soll. Viel absurder geht es kaum. Ich meine es ist dazu alles gesagt, also EOD. -- Pewa (Diskussion) 23:34, 29. Apr. 2013 (CEST)
- PS: Ich sehe hier keine Beleidigung. Dass du nicht verstehen willst, was man in Naturwissenschaft und Technik unter einem Zeiger versteht, hast du oben zur Genüge gezeigt. Du kannst auch nicht erklären, wie man mit deinem "reellen Zeigermodell" (WP:TF) rechnen kann. -- Pewa (Diskussion) 23:34, 29. Apr. 2013 (CEST)
Sagt mal: Ihr seid doch alle erwachsen, oder? Geht's Euch darum Recht zu haben, oder einen vernünftigen Artikel zu schreiben? Zum Inhaltlichen im Artikel: Ob da die komplexe Ebene erwähnt wird, oder nicht ist doch hier relativ egal (obwohl ich sie eher erwähnen würde, da das schon das "übliche" Zeigermodell ist). Wie oben schon angemerkt, kann man jede Rechnung in der komplexen Ebene natürlich auch gleichwertig für Zahlentupel aus dem R2 ausführen, nur die Schreibweise ist etwas kompakter, da die komplexe e-Funktion verwendet wird. Ich finde also diese Version ganz gut, würde darüber aber wirklich keinen seitenlangen Streit führen. Nutzt Eure Zeit lieber sinnvoller! Zum Beispiel von Pewa/Eulenspiegel oben: ??? @Eulenspiegel1: Deine Argumente verstehe ich auch nicht! Zur Darstellung des komplexen Widerstandes musst Du mindestens zwei reele Zahlen angeben, eine für Phasenverschiebung und eine für die Dämpfung. Genau deswegen ist es ja im komplexen einfacher darzustellen. Soweit von mir, alles andere könnt Ihr selber auskappeln, wenn's Euch Spaß macht, ich hab genaug im RL zu tun ... --Jkrieger (Diskussion) 08:38, 30. Apr. 2013 (CEST)
- Ergänzung: Richtig, für einen komplexen Widerstand muss man zwei Werte angeben. Entweder Realteil und Imaginärteil (Wirkwiderstand und Blindwiderstand) oder Betrag und Phasenwinkel. Beides ist gleichwertig. Nur mit einem Zeiger/komplexe Größe kann man beide (orthogonalen) Werte in einem Wert zusammenfassen, mit dem man einfach rechnen kann. -- Pewa (Diskussion) 09:29, 30. Apr. 2013 (CEST)
- Eigentlich hat JKrieger recht: Wozu der ganze Ärger? Mit Deinem letzten Diskussionsbeitrag gestehst Du (Pewa) ja sogar ein, dass auch mit rein reellen Größen geht (denn sowohl der Betrag als auch der Phasenwinkel sind reelle Zahlen). Mir ging es in der Diskussion darum, dass meine Argumente in unqualifizierter und unsachlicher Weise abgekanzelt wurden und dass sich - wenn es denn so bleibt - der größere Starrsinn durchsetzen wird. Ich bin Dir (Pewa) keine Rechenschaft darüber schuldig, was ich berechnen kann und was nicht. Deswegen darfst Du (Pewa) Dir auch kein Urteil über meine Fähigkeiten anmaßen. Es wäre auch hilfreich, wenn Du mal zwischen dem, was ich im Artikel geschrieben habe, und dem, was ich in der Diskussion sage, unterscheiden könntest. Im Artikel habe ich nie (!) das Wort reell verwendet. Ich habe mich nur dagegen gesträubt das exklusive Wort komplex zu verwenden. Meine Gründe dafür: 1) Es stellt keinen Mehrwert dar, hier die komplexe Zahlenebene zu erwähnen, weil auch dann, wenn man im Reellen arbeitet, ein klarer Unterschied zwischen den Winkelgeschwindigkeit und der Kreisfrequenz besteht. 2) Die Verwendung der komplexen Zahlenebene verwirrt all jene, die nicht wissen, was es damit auf sich hat. Trotzdem kann für sie eine klare Unterscheidung der Begriffe Winkelgeschwindigkeit und Kreisfrequenz wichtig sein, z. B. für Schüler in der gymnasialen Oberstufe (Das sind übrigens keineswegs OmA-Leser, und selbst für jene soll ja Wikipedia was taugen!). 3) Der Informationsgehalt beider Beschreibungen ist gleich, weil der und isomorph sind. In beiden Fällen handelt es sich um mathematische Modelle. Es ist also falsch, wenn man versucht zu argumentieren, was ein Zeiger „wirklich ist“. 4) Das reelle Zeigermodell wird verwendet. Ich bestreite nicht, dass an der Hochschule das komplexe Modell bevorzugt wird, weil es die Rechenarbeit (insbesondere in der Wechselstromlehre) erheblich vereinfacht, aber auch das reelle Zeigermodell hat (außerhalb der Hochschule) seine Anwendungen und damit auch seine Berechtigung, in Wikipedia gewürdigt zu werden. Aufgrund dieser Argumente wurde mir von Pewa mangelnde Fachkenntnis vorgeworfen. Immerhin kenne ich zwei Modelle, Pewa anscheinend nur eins. Das deutet nicht auf ein Defizit auf meiner Seite hin. --Pyrrhocorax (Diskussion) 11:31, 30. Apr. 2013 (CEST)
Zylinder- und Kugelkoordinaten
[Quelltext bearbeiten]Gehören Zylinder- und Kugelkoordinaten eines Ortsvektors nicht eher zum Abschnitt "Winkelgeschwindigkeit des Sehstrahls"? Bei Zylinderkoordinaten könnte man dann auch den vollständigen Ausdruck anführen.
- Die Formel für Zylinderkoordinaten war so, ohne Erklärung, falsch und ich hab sie korrigiert. Denn in Zylinderkoordinaten ist ! Mit der angegebenen Formel berechnete sich . Analoges gilt in Kugelkoordinaten, wo die angegebene Formel von meiner korrekten abwich. Evtl. sollte mein Beitrag über Zylinder- und Kugelkoordinaten wieder nach Winkelgeschwindigkeit#Winkelgeschwindigkeit bei speziellen Bewegungsansätzen verschoben werden?! --Alva2004 (Diskussion) 09:10, 12. Jun. 2017 (CEST)
- Ich hätte meinen Edit wohl ausführlicher erläutern sollen.
- Die von mir eingefügten Formeln für omega in Kugel- und Zylinderkoordinaten folgen direkt aus der oberhalb stehenden Formel mit dem Kreuzprodukt (Winkelgeschwindigkeit eines Ortsvektors).
- Was jetzt dagegen dasteht ist z.B. in Kugelkoordinaten die Winkelgeschwindigkeit für Änderung der Basis bei Variation von theta und phi. Das ist mathematisch salopp betrachtet einfach das Starrkörper-omega für z.B. Gier-Nick-Roll in z, y′, x″-Konvention aus der Fahrzeugtechnik mit . Da weiter unten dieses omega in Eulerkonvention steht, ist das damit aber eigentlich schon abgedeckt. Ich dachte daher es wäre besser, Kugel- und Zylinderkoordinaten unter den Abschnitt Sehstrahl einzuordnen, da mir diese Koordinaten bisher noch nicht im Zusammenhang mit starren Körpern begegnet sind. Wenn das so aber in manchen Fächern gemacht wird, sollte es natürlich wieder in den entsprechenden Abschnitt zurückverschoben werden (evtl. mit einem Hinweis dass der starre Körper dabei nur einen/zwei Freiheitsgrade hat).--2003:63:2B0F:6DF4:FCD6:1176:26C7:B496 19:27, 12. Jun. 2017 (CEST)
- Hallo, ich finde deine Anmerkungen interessant und die könnten doch in den Artikel aufgenommen werden? Ich hatte die Abschnitte zu den Zylinder- und Kugelkoordinaten aufgenommen, weil sie einfach nachzuvollziehen sind (im Gegensatz zu den Euler-Winkeln), für OMA also einen Aha-Effekt bringen könnten, man die Ableitung der Basisvektoren auch manchmal (nicht unbedingt bei Starrkörperbewegungen) braucht und es dann schön ist, wenn man sie irgendwo nachschlagen kann... Ich werde die Zylinder- und Kugelkoordinaten wieder nach Winkelgeschwindigkeit#Winkelgeschwindigkeit bei speziellen Bewegungsansätzen verschieben und mich freuen, wenn du einen zweiten Anlauf machst mit mehr Erklärungen zur Herleitung der Formeln und ohne die Abschnitte zu Zylinder- und Kugelkoordinaten zu löschen. --Alva2004 (Diskussion) 06:59, 15. Jun. 2017 (CEST)
- Hallo, viel zu erklären gibt es da gar nicht, finde ich. Man setzt einfach Zylinderkoordinaten ein in die Formel mit dem Kreuzprodukt und zerlegt in Basisvektoren. Lehrreich sind aber speziell Zylinderkoordinaten trotzdem, da es zunächst kontraintuitiv ist, mit einer Rotation des Ortsvektors zu verbinden. Ich ergänze darum mal die beiden Fälle mit einer kurzen Erklärung zur Rechnung. Stärker betonen sollte man imo dass es sich einmal um omega bzgl. eines ruhenden Beobachters (omega abhängig vom Beobachtungspunkt), das andere Mal bzgl. eines körperfesten Punktes handelt (omega eindeutig). Das habe ich erst nicht gemerkt und deswegen Zylinder- und Kugelkoordinaten ganz nach Sehstrahl verschoben.--2003:63:2B02:63F2:691C:B648:5EDE:DBAB 21:34, 15. Jun. 2017 (CEST)
- Hallo, ich finde deine Anmerkungen interessant und die könnten doch in den Artikel aufgenommen werden? Ich hatte die Abschnitte zu den Zylinder- und Kugelkoordinaten aufgenommen, weil sie einfach nachzuvollziehen sind (im Gegensatz zu den Euler-Winkeln), für OMA also einen Aha-Effekt bringen könnten, man die Ableitung der Basisvektoren auch manchmal (nicht unbedingt bei Starrkörperbewegungen) braucht und es dann schön ist, wenn man sie irgendwo nachschlagen kann... Ich werde die Zylinder- und Kugelkoordinaten wieder nach Winkelgeschwindigkeit#Winkelgeschwindigkeit bei speziellen Bewegungsansätzen verschieben und mich freuen, wenn du einen zweiten Anlauf machst mit mehr Erklärungen zur Herleitung der Formeln und ohne die Abschnitte zu Zylinder- und Kugelkoordinaten zu löschen. --Alva2004 (Diskussion) 06:59, 15. Jun. 2017 (CEST)
Winkelgeschwindigkeit definieren, ohne von Drehachse zu sprechen
[Quelltext bearbeiten]Ausgelöst durch die lange aktuelle Diskussion zu Corioliskraft fällt auf, dass eine Drehachse gar nicht nötig ist, um die Größe Winkelgeschwindigkeit präzise zu definieren. Ich denke an einen entsprechenden (ergänzenden) Abschnitt hier:
- Definition ohne Bezugnahme auf eine Drehachse
- Die Angabe einer Winkelgeschwindigkeit setzt nicht voraus, dass überhaupt eine bestimmte Achse zugrundegelegt ist. Es genügt die Angabe, mit welcher Geschwindigkeit sich eine Richtung im Raum ändert. Hat die Richtung sich im (infinitesimalen) Zeitintervall um den Winkel geändert, so ist die Winkelgeschwindigkeit einfach . Die veränderliche Richtung kann zum Beispiel durch den Geschwindigkeitsvektor eines Autos auf einer kurvigen Strecke gegeben sein. Dass das Auto zu verschiedenen Zeiten auch an verschiedenen Orten ist, spielt für den Vergleich der jeweiligen Fahrtrichtungen keine Rolle. Eine Anwendung dieser Definition findet sich z. B. in der einfachen Herleitung der Zentripetalkraft.
- Bleibt die veränderliche Richtung im Zeitintervall in einer Ebene, kann man die Richtungsänderung zu jedem Zeitpunkt als Drehung um eine Achse auffassen, die senkrecht auf dieser Ebene steht, aber sonst frei wählbar ist. Dann lässt sich der Winkelgeschwindigkeit ein Vektor zuordnen, der den Betrag hat, zur Achse parallel liegt und in die Richtung des Kreuzprodukts zeigt.
Selbstanzeige wg. TF: Leider kann ich kein Buch als Beleg anführen. Vielleicht hat jemand eine bessere Bibliothek in Reichweite, mit dem Landau-Lifschitz etc.? --Bleckneuhaus (Diskussion) 13:09, 5. Jan. 2021 (CET)
- Das Auto-Beispiel wäre in der Fahrdynamik die Kurswinkelgeschwindigkeit. Also keine TF.--Wruedt (Diskussion) 21:05, 5. Jan. 2021 (CET)
Der Umstand, dass die Winkelgeschwindigkeit eines starren Körpers unabhängig von der Lage der Rotationsachse der Bewegung ist, fehlt in der Tat bisher im Artikel. Das ist ein relevanter Umstand, der einen eigenen Abschnitt wert ist. Den oben versuchten Ansatz, explizite Rotationsbewegungen und die damit verbundene Rotationsachse zu vermeiden und stattdessen auf Differentialrechnung zu setzen, versteht man leider nur, wenn man die diversen Begriffe und Konzepte schon verstanden und verinnerlicht hat.
Jede Bewegung mit von Null verschiedener Winkelgeschwindigkeit hat zu jedem Moment eine eindeutig definierte Rotationsachse. Lage und Ausrichtung der Rotationsachse sind im allgemeinen zeitabhängig. Es ist aber didaktisch sinnvoll, zunächst den Spezialfall zu betrachten, bei dem sich die Lage und Ausrichtung der Rotationsachse nicht verändert. Als konkretes, allgemein bekanntes Beispiel würde ich den Rotor eines Hubschraubers vorschlagen. Jeder einzelne Flügel die gleiche Winkelgeschwindigkeit. ---<)kmk(>- (Diskussion) 22:47, 5. Jan. 2021 (CET)
- Erstmal danke für den etablierten Begriff Kurswinkelgeschwindigkeit, auch wenn der via Google nicht so häufig vorkommt. Zu -<)kmk(>-: Ich verstehe Deine Einwände nicht, wenn es denn solche sein sollten. Bist Du denn nun dagegen, so einen Abschnitt mit aufzunehmen? Im Einzelnen zu Deiner Antwort:
- Winkelgeschwindigkeit eines starren Körpers unabhängig von der Lage der Rotationsachse der Bewegung fehlt mit auch, sollte rein.
- Rotationsachse zu vermeiden ist gar nicht mein Ziel, sondern eine ergänzende Herleitung des Begriffs zu bringen.
- stattdessen auf Differentialrechnung zu setzen - 1. nicht stattdessen (s. vorigen Punkt), 2. kommt der Artikel selbst ja auch gleich mit einem Diff-Quotienten.
- zunächst den Spezialfall zu betrachten - ja klar, aber wieso spricht das dagegen, eine andere und sogar noch allgemeinere Hinführung zum Lemma zu bringen?
- In (#Winkelgeschwindigkeit des starren Körpers) ist doch das wesentliche dargestellt, nämlich die Unabhängigkeit von der Laqe der Rotationsachse. Bezugssystem findet sich auch drin, wobei man hier vielleicht konkreter von Koordinatensystem sprechen könnte. Was also soll in einen extra Abschnitt, was im angesprochenen Abschnitt nicht drin ist. Zwar hat jede Bewegung eines Starrkörpers eine Schraubachse, blos wer würde schon zu jedem Zeitpunkt ein anderes BS definieren wollen, nur dass es ein rotierendes ist. Die ständige Verkürzung auf diesen Spezialfall ist unnötig und verstellt den Blick auf den allgemeinen Fall.--Wruedt (Diskussion) 10:54, 6. Jan. 2021 (CET)
Wahrscheinlich oute ich mich durch das folgende als eine physikalische omA, aber vielleicht könnt Ihr mir ja auf die Sprünge helfen, wenn ich da was was falsch verstanden habe. Ich glaube, dass in dieser Diskussion und auch im Abschnitt über den Starren Körper gar nicht gewürdigt wird, dass es verschiedene Arten der Winkelgeschwindigkeiten gibt. Wenn ich mit der Winkelgeschwindigkeit ein Maß für die Drehung der Achsen eines Körpers meine, dann ist das natürlich unabhängig von der Wahl des Bezugspunkts. Wenn ich damit aber die Drehung des Ortsvektors des Schwerpunkts eines starren Körpers meine, dann ist das natürlich abhängig von der Wahl des Bezugspunkts. Dass wir beide Begriffe gerne miteinander verwechseln, liegt daran, dass es viele Beispiele gibt, in denen beide Bewegungen gekoppelt sind. In einem Karussell dreht sich das Karussell exakt mit derselben Winkelgeschwindigkeit wie die Fahrgäste. In einem Riesenrad aber nicht: Hier beträgt die Eigenrotationsrate der Kabinen Null (denn der Boden ist immer unten). Trotzdem haben die Kabinen selbstverständlich eine Winkelgeschwindigkeit bezogen auf die Nabe des Riesenrads. Anderes Beispiel: Ein Auto hat in Geradeausfahrt eine Eigenrotationsrate von Null (denn die Richtung von ändert sich ja nicht). Trotzdem kann man dem Auto eine Winkelgeschwindigkeit bezüglich einer beliebigen Drehachse (und damit auch einen Drehimpuls) zuordnen. Winkelgeschwindigkeit und Drehimpuls sind nur dann Null, wenn als Bezugspunkt ein Punkt auf der Fahrbahn gewählt wird.--Pyrrhocorax (Diskussion) 14:35, 6. Jan. 2021 (CET)
- Ist alles richtig, würde ich sagen. --Bleckneuhaus (Diskussion) 17:56, 6. Jan. 2021 (CET)
- Die Winkelgeschwindigkeit ist nur bei einem starren Körper eindeutig. Die Kabine eines Riesenrads kann man als starren Körper auffassen. Hier kann man die Bewegung eindeutig in Translation und Rotation aufteilen. Das Riesenrad als Ganzes ist jedoch kein starrer Körper mehr. Hier gilt dann nicht mehr die Eindeutigkeit der Winkelgeschwindigkeit. --Eulenspiegel1 (Diskussion) 18:41, 6. Jan. 2021 (CET)
- Das Rad an dem die Kabinen aufgehängt sind, kann wieder als starrer Körper aufgefasst werden. Wer hat denn behauptet dass man den Begriff Winkelgeschwindigkeit auf beliebige Körper anwenden kann. Das Thema lautet, dass man keine Rotationsachse benötigt um eine Winkelgeschwindigkeit zu definieren (bei solchen Körpern wo das Sinn macht)
- PS: Im Fall der Kurswinkelgeschwindigkeit ist das noch nicht mal ein starrer Körper, sondern die Winkelgeschwindigkeit des Geschwindigkeitsvektors. Dieser ist nicht fest ans Auto gebunden, sonst könnt man noch nicht mal Wenden.--Wruedt (Diskussion) 20:07, 6. Jan. 2021 (CET)
- Man kann den Begriff Winkelgeschwindigkeit auf beliebige Körper anwenden. Aber nur bei starren Körpern ist er eindeutig. Bei nicht-starren Körpern ist die Winkelgeschwindigkeit vom Bezugspunkt abhängig.
- Zur oberen Gleichung:
- Die Änderung der Beschleunigung ist nicht die Winkelgeschwindigkeit. Bei einem beschleunigenden Auto ändert sich aufgrund der Luftreibung auch die Beschleunigung, ohne dass das Auto deswegen eine Kurve fährt.
- Bei Rotationen ohne Drehmoment könnte man die Winkelgeschwindigkeit noch über die Periode definieren: .
- Abgesehen von diesem Spezialfall (ohne Drehmoment) ist mir kein Lehrbuch bekannt, in dem die Winkelgeschwindigkeit ohne Drehachse definiert wird.
- Zum PS: Kurswinkelgeschwindigkeit ist etwas anderes als Winkelgeschwindigkeit. --Eulenspiegel1 (Diskussion) 11:42, 7. Jan. 2021 (CET)
Wo kann man Kurswinkelgschwindigkeit definiert finden? M.E. trifft der Begriff genau das, was ich meinte. --14:59, 7. Jan. 2021 (CET) (unvollständig signierter Beitrag von Bleckneuhaus (Diskussion | Beiträge) )
- In WP in Einspurmodell. In der Normung nur Kurswinkel definiert. Sonst ev. in Fachliteratur z.B. bei Mitschke.--Wruedt (Diskussion) 17:05, 7. Jan. 2021 (CET)




























































![{\displaystyle [{\vec {v}}(t)\times {\vec {v}}(t+\Delta t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a75070c1c5652f6664098ab92d1611005bf541b)
